Разработка урока внеурочной деятельности Задачи с избыточным условием

Урок № 47-49

Логика 5 класс

Тема: «Задачи с неполными данными, лишними, нереальными данными. Решение задач с неполными данными».

Цель:

• познакомить ребят с понятиями задача с неполными данными, лишними или нереальными;

• научить их решать такие задачи;

• научить их придумывать такие задачи;

• способствовать развитию умений анализировать, сравнивать, обобщать, выделять главное; развивать осознанную математическую речь; развитие познавательного интереса учащихся;

• содействовать воспитанию таких качеств как: самостоятельность, целеустремленность, настойчивость, целенаправленность, трудолюбие, аккуратность, ответственность

Задачи:

- Продолжить формирование навыков контроля результатов деятельности.

- Способствовать развитию коммуникативных навыков. Развивать умение анализировать, обобщать материал, выступать перед аудиторией, развивать интеллектуальные, творческие и исследовательские способности, активизировать интерес к учебным предметам.

- Формирование логического, абстрактного, эвристического, системного мышления.

Оборудование: проектор, экран, компьютер, презентации

План.

1. Организационные моменты

2. Что такое задача с неполными данными, лишними или нереальными.

Какие задачи относятся к задачам с недостающими данными, а какие − к задачам с избыточными данными? Как получить недостающие данные? Что делать с избыточными данными? На эти вопросы ответим на этом занятии.

Рассмотрим задачу:

Чтобы ответить на требование задачи, нужно число, обозначающее количество мальчиков, умножить на 2, так как девочек в 2 раза больше. Но мы не знаем, сколько мальчиков. Для решения задачи не хватает данных, а именно не указано число мальчиков.

Задачу, требования которой нельзя выполнить из-за отсутствия необходимых данных, называют задачей с недостающими данными.

Чтобы её решить, нужно дополнить условие задачи необходимыми данными. Такие данные называются дополнительными.

Дополним нашу задачу дополнительными данными: мальчиков в классе 8. Теперь задачу можно решить:

8 ∙ 2 = 16

Ответ: 16 девочек было в классе.

Заметим, что дополнять задачу нужно только такими данными, с помощью которых можно решить задачу. Например:

Дополнительными данными могут быть только числа, которые делятся на 3, иначе задачу нельзя решить.

Кроме этого, нельзя брать в качестве дополнительных данных числа, которые не могут соответствовать действительности. Например, количество конфет в коробке не может быть 600. Можно решить задачу с этим числом и получить ответ, но ответ не будет соответствовать реальной жизни.

Иногда дополнительные данные можно получить.

Например, для решения практических задач, когда можно выполнить необходимые измерения. Так, чтобы решить задачу: найти периметр комнаты, нужно измерить длину и ширину комнаты. Таким образом, недостающие данные мы получим в результате измерения длины и ширины комнаты.

Величины для решения задач с недостающими данными можно взять из справочной литературы. Например, возьмем задачу:

Чтобы её решить, дополнительные данные можно взять из учебника географии или справочной литературы. Можно найти эти данные и в сети Интернет.

В жизни, как правило, необходимые данные человек добывает сам, выполняя необходимые измерения, проводя опыты, изучая справочную литературу.

Перейдем к задачам другого вида.

Чтобы ответить на требование данной задачи нужно к 15 прибавить 6, так как на второй полке на 6 книг больше.

15 + 6 = 21

21 книга на второй полке. При решении задачи использовались не все данные условия, а именно «на третьей полке книг в 3 раза больше, чем на первой». Эти данные лишние, их называют избыточными.

Задачи, в которых есть лишние данные, то есть данные, которые не нужны для решения задачи, называются задачами с избыточными данными.

Что делать с избыточными данными? Иногда избыточные данные помогают найти разные способы решения задачи. Рассмотрим это на примере. Задача:

Ответить на требование задачи можно одним действием:

27 + 29 = 56 (уч.) - в двух классах.

При этом остальные данные задачи будут избыточными. Ответим на требование задачи, не используя данные 27 и 29. В этом случае возможны два способа решения задачи. Можно сначала узнать, сколько детей в каждом классе:

14 + 13 = 27 (уч.) - в 3 «а» классе

15 + 14 = 29 (уч.) - в 3 «б» классе

затем сложить полученные результаты:

27 + 29 = 56 (уч.) - всего в двух классах.

Или можно сначала узнать, сколько всего девочек в двух классах:

14 + 15 = 29

потом - сколько мальчиков в двух классах:

13 + 14 = 27

и сложить результаты:

29 + 27 = 56 (уч.) - всего в двух классах.

Таким образом, избыточные данные помогают найти разные способы решения задачи, важно при этом выбрать рациональный способ.

Как правило, избыточные данные присутствуют в практических задачах. Например, в продуктовом магазине есть ценники на всех товарах, но сумму покупки будет составлять только стоимость тех товаров, которые купили.

На этом уроке мы выяснили, что задачи могут быть с недостающими данными или с избыточными данными и научились их решать.

3. Решение задач с неполными данными, лишними, нереальными данными.

1. Основные составляющие задачи

Повторим основные составляющие любой математической задачи. Для этого представим структуру задачи с помощью следующего рисунка:

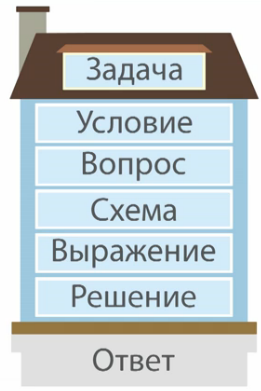
2. Задание на проверку правильности составления задач

Итак, задачи состоят из следующих логических частей:

1. Условие - это то, что известно в задаче;

2. Вопрос - это то, что надо найти;

3. Схема - краткая запись содержания задачи;

4. Выражение и его значение;

5. Решение задачи;

6. Ответ - значение составленного выражения.

3. Задача №1 с ошибочным вопросом

Задание 1:

Незнайка придумал свои математические задачи. Нужно проверить, можно ли эти тексты назвать задачами.

«На кочке сидели 4 лягушки. Одна прыгнула в воду. Сколько лягушек прыгнуло в воду?»

В этой задаче есть условие: «На кочке сидели 4 лягушки. Одна прыгнула в воду». Есть вопрос: «Сколько лягушек прыгнуло в воду?».

Однако, в этом тексте ошибка. Число лягушек, прыгнувших в воду, есть в условии - «одна». То есть в вопросе просят узнать то, что известно.

Уберем ошибочный вопрос и изменим вопрос так, чтобы надо было найти неизвестное.

«Сколько лягушек осталось на кочке?». В результате получилась задача:

«На кочке сидели 4 лягушки. Одна прыгнула в воду. Сколько лягушек осталось на кочке?».

Решение:

Сделаем краткую запись задачи с помощью схемы:

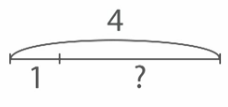
На схеме видно, что надо найти часть. Чтобы найти часть, надо из целого вычесть другую часть. Запишем выражение и найдем его значение:

Ответ: 3 лягушки остались на кочке.

4. Задача №2 с нереальным условием

Нереальными задачами будем называть задачи, числовые данные которых делают их лишенными смысла (по В.А. Крутецкому). Каждая из этих задач является типовой, но числовые данные делают ее нереальной. Например:

1. Периметр прямоугольника 8 см, а сумма двух его сторон 6 см. Найти длину стороны.

2. Иван на два года моложе Петра, Петр четырьмя годами старше Степана, Андрей на три года старше, чем Петр, Иван равен по возрасту Степану. Кто старше - Андрей или Иван?

3. «Мама купила 5 пачек соли. Две съели за обедом. Сколько пачек соли осталось?»

В этой задаче есть условие: «Мама купила 5 пачек соли. Две съели за обедом». Есть вопрос: «Сколько пачек соли осталось?». Значит, это задача.

Но в этой задаче нереальное условие: за обедом съели 2 пачки соли. Это невозможно, поэтому нет смысла решать эту задачу.

Таким образом простая задача «достраивается» до составной.

Применение при обучении решению задач с недостающими и избыточными данными, нереальных задач имеет большое значение. При помощи этих задач можно не только выяснить насколько дети понимают связи в задаче, но и при работе над одной задачей с избыточными данными иногда удается составить и решить еще несколько задач, что является одним из приемов насыщения уроков задачами.

Например:

1. Маша отдала несколько открыток подруге, после чего у нее осталось 5 открыток. Сколько открыток отдала Маша подруге?

После выяснения, какого данного не хватает для возможности решения задачи, ученикам можно предложить самостоятельно подобрать, сколько открыток было у Маши, и решить при этом несколько задач вместо одной.

2. К чаю подали 9 пирожных «эклер», 6 пирожных «корзиночек» и 12 шоколадных конфет. Съели 11 пирожных. Сколько пирожных осталось?

Следует выяснить, какие данные лишние, как изменить вопрос или что изменить в условии, чтобы использовать все данные. Опять решается не одна, а несколько задач.

5. Задача №3 без вопроса

«У Коли 2 мячика, у Саши 3 мячика».

В этом тексте есть условие: «У Коли 2 мячика, у Саши 3 мячика», - но нет вопроса.

Для того чтобы этот текст стал задачей, необходимо к этому условию добавить вопрос: «Сколько всего мячиков у мальчиков?»

Теперь получилась задача: «У Коли 2 мячика, у Саши 3 мячика. Сколько всего мячиков у мальчиков?».

Решение: Сделаем краткую запись этой задачи с помощью схемы.

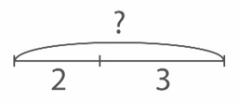
На схеме видно, что надо найти целое. Для этого надо сложить части. Запишем и найдем значение выражения:

Ответ: У мальчиков всего 5 мячиков.

6. Задача №4 без условия

«Сколько стоят 2 матрешки?»

В этом тексте есть вопрос: «Сколько стоят 2 матрешки?». Однако, в этом тексте нет условия.

Для того чтобы сделать задачу из этого текста, добавим к вопросу условие: «Одна матрешка стоит 5 рублей, а вторая - 4 рубля».

В результате получим задачу: «Одна матрешка стоит 5 рублей, а вторая - 4 рубля. Сколько стоят 2 матрешки?»

Решение: Сделаем краткую запись этой задачи с помощью схемы.

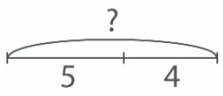
Для того, чтобы найти целое, надо сложить его части. Запишем и найдем значение выражения:

Ответ: 2 матрешки стоят 9 рублей.

7. Задача №5 с лишними данными

«Карлсон съел на завтрак 5 булочек, 6 мороженых, 2 ананаса, 3 шоколадки и 4 груши. Сколько фруктов съел Карлсон на завтрак?»

В этом тексте есть условие: «Карлсон съел на завтрак 5 булочек, 6 мороженых, 2 ананаса, 3 шоколадки и 4 груши». Есть вопрос: «Сколько фруктов съел Карлсон на завтрак?».

В условии задачи говорится, что Карлсон съел не только фрукты, но и другие продукты, что является лишними данными. При решении задачи их использовать не надо, поэтому эти данные нужно убрать.

В результате получится следующее условие: «Карлсон съел на завтрак 2 ананаса и 4 груши. Сколько фруктов съел Карлсон на завтрак?».

Решение: Сделаем краткую запись содержания задачи с помощью схемы.

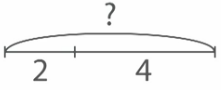
На схеме видно, что надо найти целое. Для этого надо сложить части. Запишем и найдем значение выражения:

Ответ: Карлсон съел 6 фруктов.

8. Задача №6 с неуместным вопросом

«Золушка перебрала за день 3 мешка с рисом и 4 мешка с гречкой. Сколько раз танцевала на балу Золушка с Принцем?»

В этом тексте есть условие: «Золушка перебрала за день 3 мешка с рисом и 4 мешка с гречкой». Есть вопрос: «Сколько раз танцевала на балу Золушка с Принцем?».

Однако условие задачи не связано с вопросом, значит, его нужно изменить. В результате получим задачу: «Золушка перебрала за день 3 мешка с рисом и 4 мешка с гречкой. Сколько всего мешков крупы перебрала Золушка?».

Решение: Для того чтобы ответить на вопрос задачи, составим схему, потом выражение и найдем его значение.

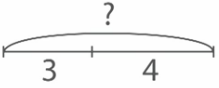
Сложим части целого, чтобы записать и найти значение выражения:

Ответ: Золушка перебрала 7 мешков крупы.

У кормушки было 6 серых и 5 белых голубей. Один белый голубь улетел. Сколько белых голубей стало у кормушки?

Анализ текста показывает, что одно из данных лишнее - 6 серых голубей. Для ответа на вопрос оно не нужно. После решения задачи учитель предлагает внести в текст задачи такие изменения, чтобы это данное понадобилось. Это приводит к составной задаче:

Задача.

У кормушки было б серых и 5 белых голубей. Один голубь улетел. Сколько голубей осталось у кормушки?

Эти изменения условия повлекут за собой необходимость выполнять два действия:

(6 + 5) - 1 или (6 - 1) + 5 или (5 - 1) + 6.

Задачи с избыточными данными могут быть противоречивыми и непротиворечивыми.

Детям обязательно нужно показывать такие задачи.

Рассмотрим работу над задачами такого вида на конкретных примерах. Даны задачи: а) «Дети сорвали 24 яблока. 8 яблок они съели, а остальные поделили поровну. Сколько яблок получил каждый ребенок?»; б) «Таня и Сережа сорвали 18 яблок. Таня сорвала 6 яблок, а Сережа в 2 раза больше. Сколько яблок сорвал Сережа?»; в) «Таня и Сережа сорвали 18 яблок. Таня сорвала 6 яблок, а Сережа в 3 раза больше. Сколько яблок сорвал Сережа?». Составим схемы разбора каждой из предложенных задач.

Задача а)

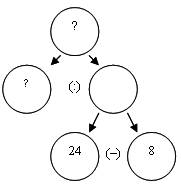
Задача (а) является задачей с недостающими данными. Она напоминает деформированную задачу, однако, в отличие от деформированной задачи, не имеет «окошка», т.е. конкретного указания на то, что пропущено данное. Эту задачу можно использовать для составления каскада задач.

Задачи (б) и (в) являются задачами с избыточными (лишними) данными. Однако одна из них может быть решена и непротиворечива, а другая не имеет однозначного решения, данные в ней противоречат друг другу.

Задача б)

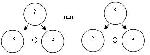
Данная задача, решенная с использованием каждой пары данных, дает одинаковый ответ (12 яблок сорвал Сережа). Таким образом, эта задача не содержит противоречивых данных.

Задача в)

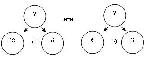
Эта задача, решенная с использованием каждой пары данных, дает разные ответы, которые противоречат друг другу: Сережа сорвал 12 яблок, и Сережа сорвал 18 яблок. Таким образом, задача не имеет однозначного решения.

</ Примеры задач:

1. Проверить, можно ли приведенные ниже тексты назвать задачами. После проверки исправить условие так, чтобы получилась правильно составленная задача, и решить ее.

«В автобусе ехало 36 человек. Сколько человек осталось в автобусе после того, как на остановке вышли 39 человек?»

«На столе лежало 7 груш, 3 розы, 5 яблок и 4 гвоздики. Сколько цветов лежало на столе?»

«Чтобы украсить класс, ребята принесли 5 ваз с цветами и еще 3 гвоздики. Сколько всего цветов принесли ребята?»

«В ларек привезли ящики с яблоками. Сколько продали ящиков, если осталось 9 ящиков?»

2. Решить задачи на повторение:

1. На верхней полке было 5 книг, а на нижней - на 4 книги больше. Сколько книг было на нижней полке?

2. Брату 13 лет, а сестра - на 4 года моложе. Сколько лет сестре?

3. У Дениса 19 марок, а у Алеши - на 3 марки меньше. Сколько марок у Алеши?

4. Дима нашел 10 белых грибов, а Сережа - на 3 гриба больше. Сколько грибов нашел Сережа?

5. В нашем подъезде 20 квартир, а в соседнем - на 2 квартиры меньше, чем в нашем. Сколько квартир в соседнем подъезде?

4. Итоги урока

Подобная динамика работы с задачами, основанная на идеях укрупнения дидактических единиц, раскрывает и приводит в действие большие резервы человеческого мозга, развивает интеллектуальную сферу ученика.

Очень важно подобрать посильные для обучающихся задания, соответствующие их возможностям, развитию. Ведь часто бывает, что даже смышленый обучающийся не хочет просто прочитать задачу, не то что решать ее, а поэтому целесообразно использовать внешнюю занимательность текстов. Цель может быть достигнута, если условие задачи будет похоже на сказку.

5. Домашнее задание.

Придумать задачу с неполными данными, лишними, нереальными данными.

12