- Учителю
- Программа элективного курса Исследование квадратного трёхчлена 9 класс
Программа элективного курса Исследование квадратного трёхчлена 9 класс
Элективный курс
« Исследование квадратного трёхчлена»
Пояснительная записка
Математическое образование в системе общего образования занимает одно из ведущих мест, что определяется безусловной практической значимостью математики, её возможностями в развитии и формировании мышления человека, её вкладом в создание представлений о научных методах познания действительности.
Актуальным остаётся вопрос дифференциации обучения математике, позволяющий, с одной стороны, обеспечить базовую математическую подготовку, а с другой стороны - удовлетворить потребности каждого, кто проявляет интерес и способности к математике.
Программа курса «Исследование квадратного
трёхчлена» предполагает изучение таких вопросов, которые не входят
в школьный курс математики основной школы, но часто встречаются в
экзаменационных заданиях. Рассматриваемая тема позволяет сделать
достаточно полный обзор не только изучаемых в школьном курсе формул
корней уравнения ![]() и формул Виета, выражающих зависимость между корнями квадратного
уравнения и его коэффициентами, но и теорем о расположении корней
квадратного трёхчлена на координатной прямой. Практическая часть
составлена из заданий с параметрами, что будет способствовать
развитию логического мышления, приобретению опыта работы с
заданиями более высокой по сравнению с обязательным уровнем
сложности, формированию математической культуры учащихся.
и формул Виета, выражающих зависимость между корнями квадратного
уравнения и его коэффициентами, но и теорем о расположении корней
квадратного трёхчлена на координатной прямой. Практическая часть
составлена из заданий с параметрами, что будет способствовать
развитию логического мышления, приобретению опыта работы с
заданиями более высокой по сравнению с обязательным уровнем
сложности, формированию математической культуры учащихся.
Целями данного курса являются:
-
Создание условий для самореализации учащихся в процессе учебной деятельности.
-
Развитие математических, интеллектуальных способностей учащихся, обобщение умственных умений.
Для достижения поставленных целей в процессе обучения решаются следующие задачи:
-
Выделение логических приёмов мышления и способствование их осмыслению, развитие образного и ассоциативного мышления.
-
Обеспечение диалогичности процесса обучения.
Курс предназначен для учащихся 9 классов и рассчитан на 8,5 часов аудиторного времени.
Курс призван помочь учащимся в овладении навыком решения заданий с параметрами, повысить уровень общей математической культуры, оценить потенциал для дальнейшего обучения в профильной школе.
В результате изучения курса учащиеся должны уметь:
-
Свободно оперировать аппаратом алгебры при решении задач на исследование квадратного трёхчлена.
-
Применять формулы корней квадратного трёхчлена, теорему Виета и теоремы о расположении корней квадратного трёхчлена на координатной прямой для решения заданий с параметрами.
Тематическое планирование
лекции
практические
1
Теорема Виета
1
2
2
Теоремы о расположении корней квадратного трёхчлена на координатной прямой
1
2
3
Задания на определение количества корней квадратного трёхчлена
-
2
4
Выходной контроль
-
0,5
Исследование квадратного трёхчлена
Теорема Виета
Между корнями ![]() и
и![]()
![]() квадратного
трёхчлена
квадратного
трёхчлена ![]() и коэффициентами существуют соотношения:
и коэффициентами существуют соотношения:
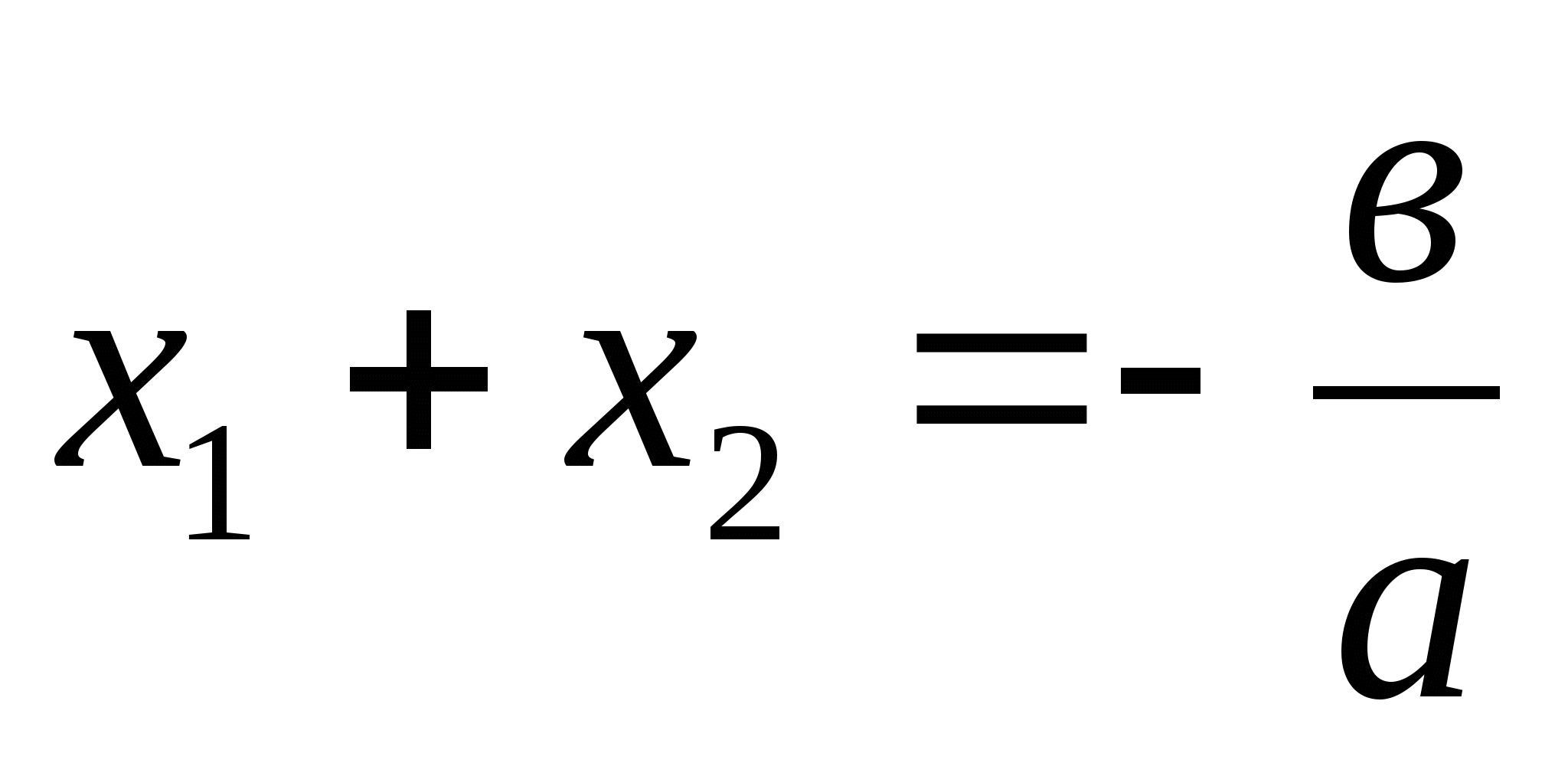 ;
;
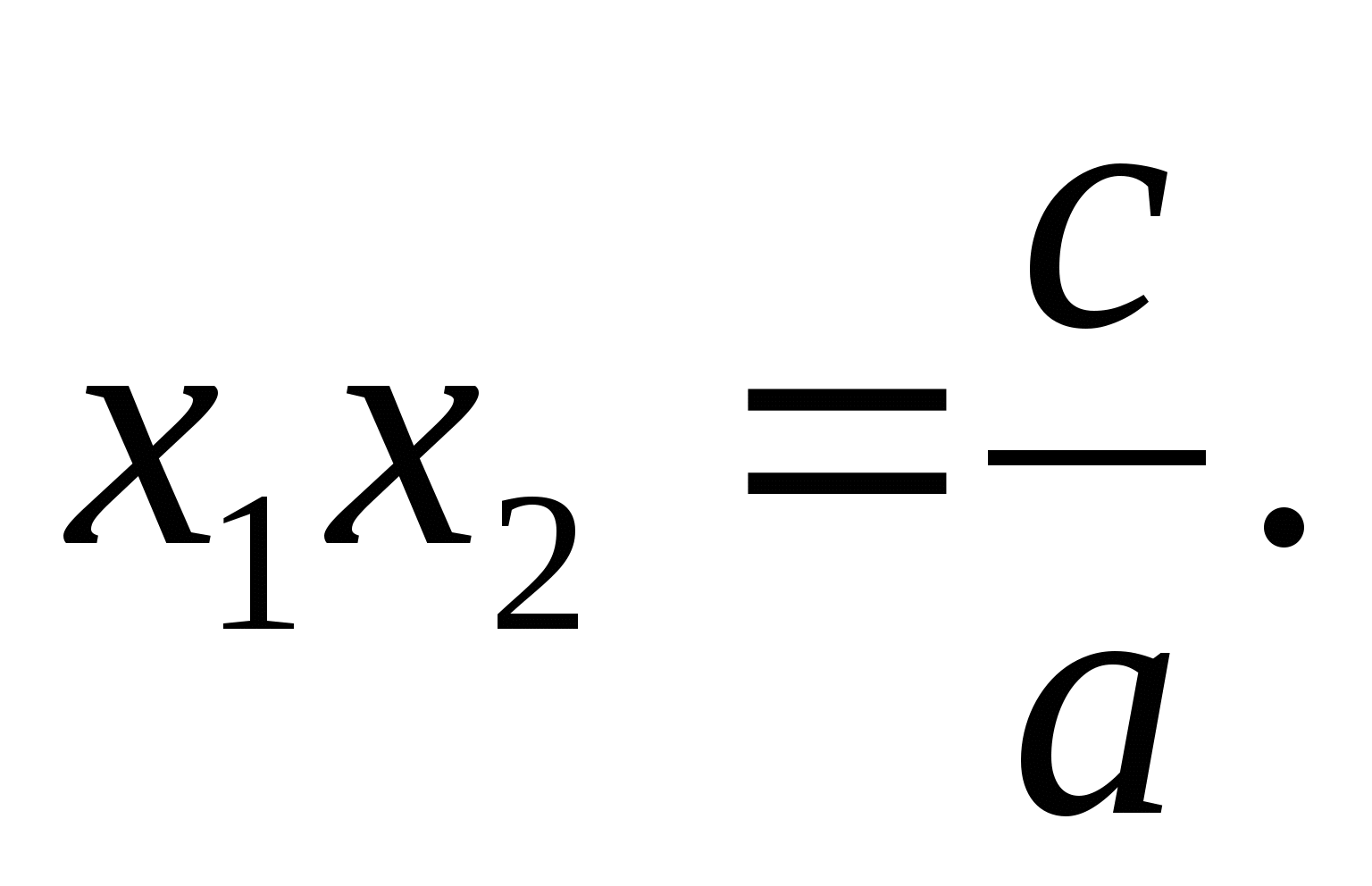
При помощи этих соотношений исследуются знаки корней.
Теорема 1. Чтобы корни квадратного трёхчлена были действительными и имели одинаковые знаки, необходимо и достаточно выполнения следующих условий:
![]()
![]()
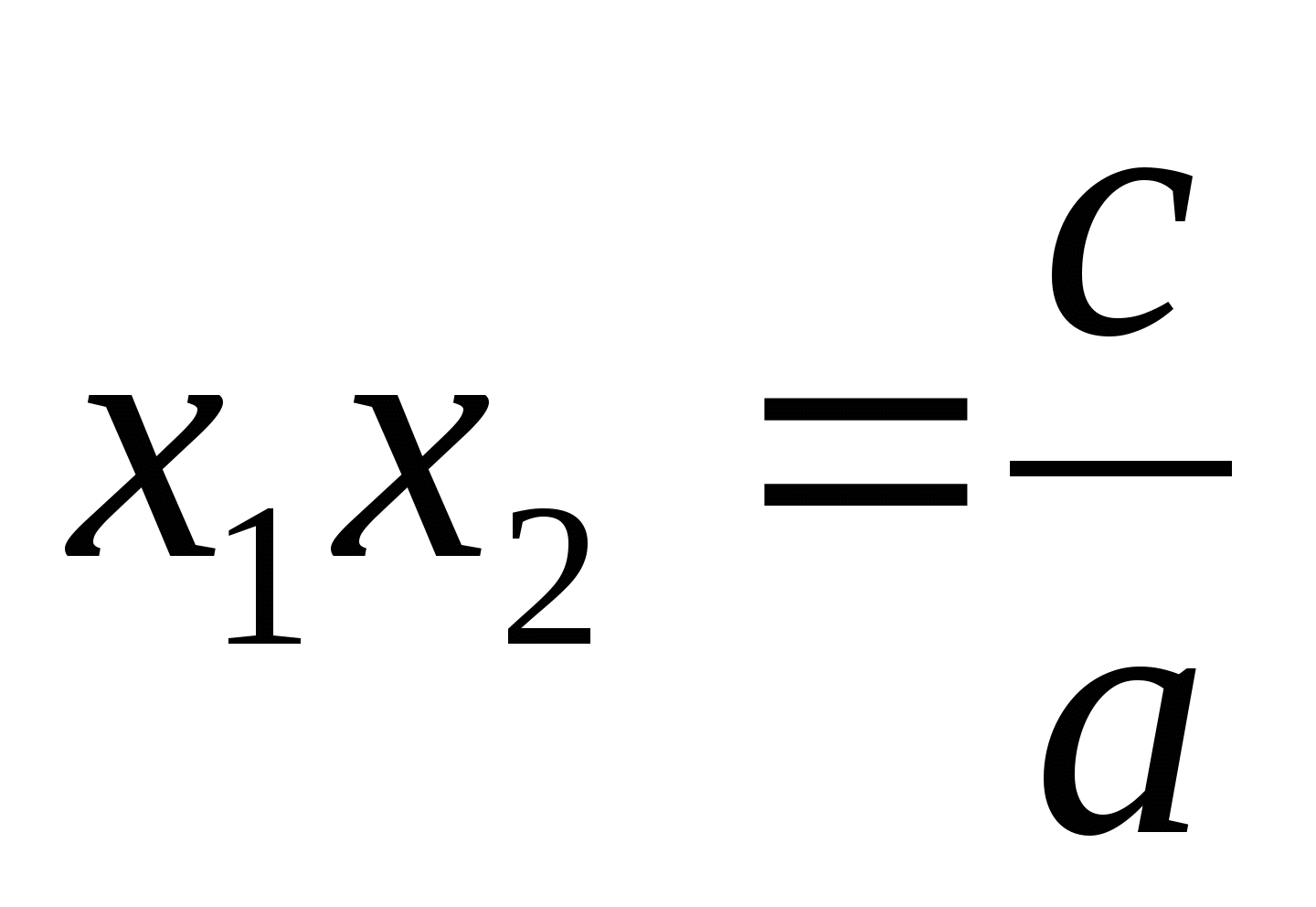 >
>
![]()
при этом оба корня будут положительными, если дополнительно наложить условие:
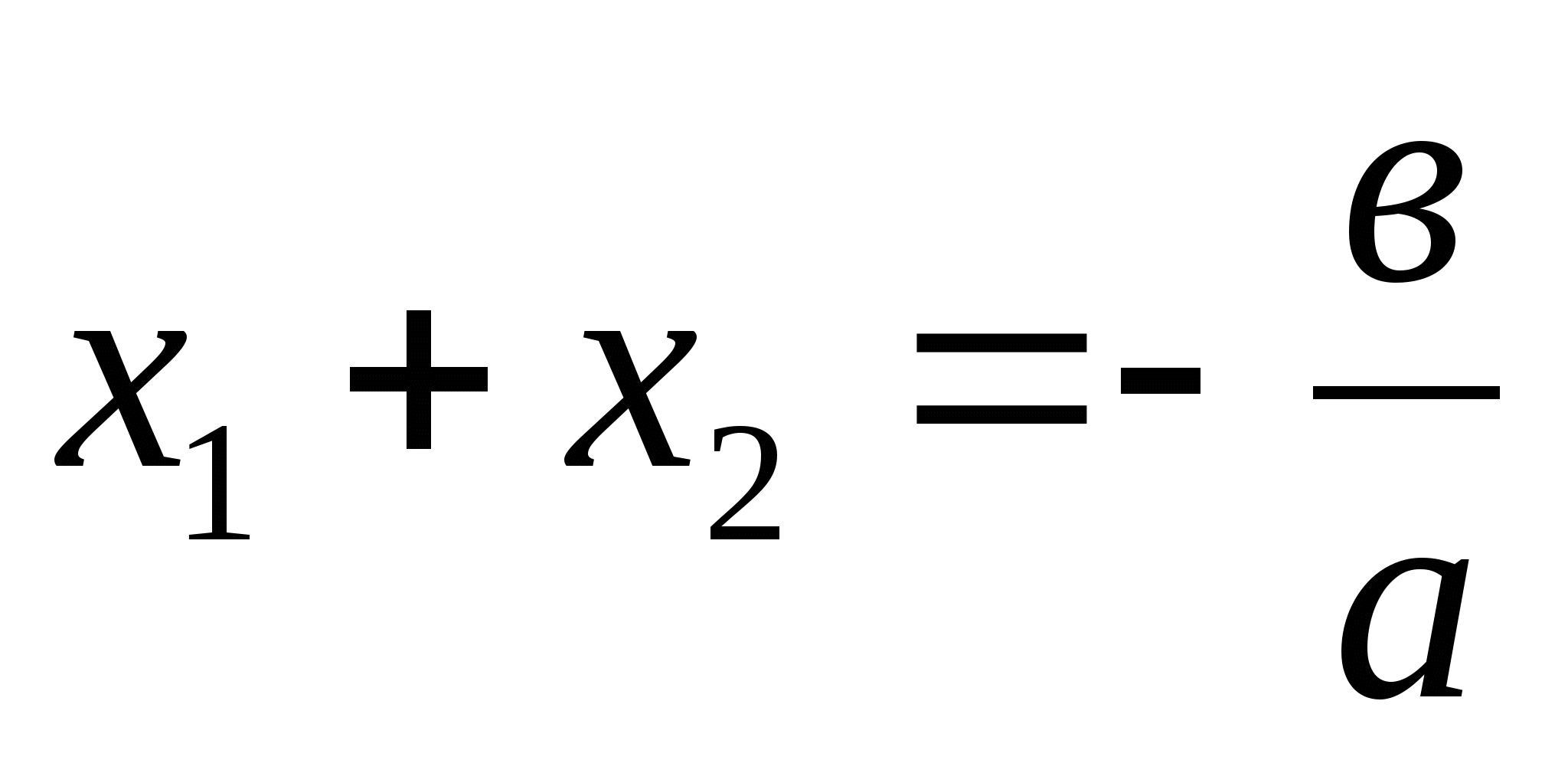 >
>
![]()
и оба корня будут отрицательными, если
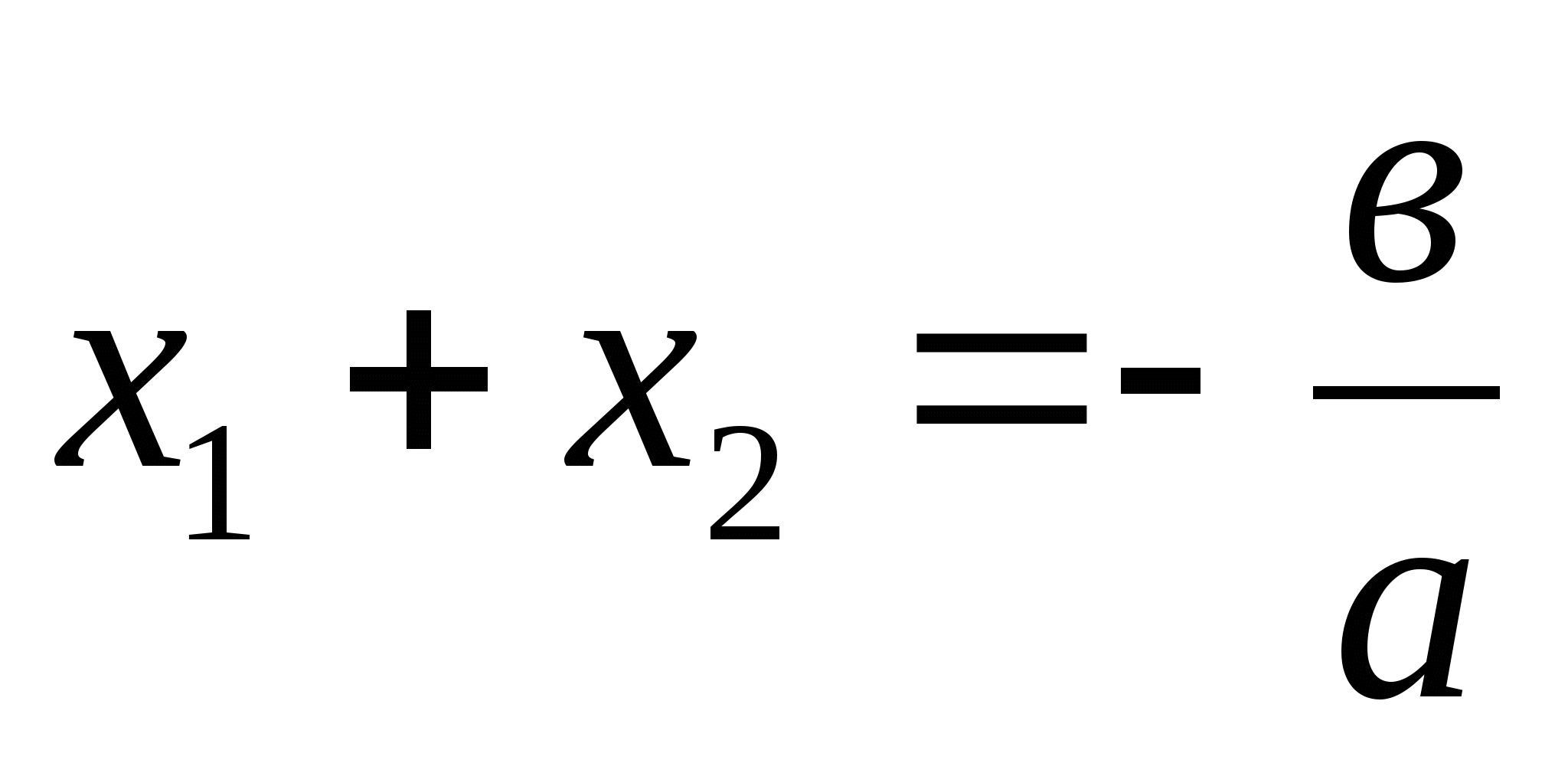 <
<
![]()
Теорема 2. Чтобы корни квадратного трёхчлена были действительными и имели разные знаки, необходимо и достаточно выполнения следующих соотношений:
![]()
![]() >
>
![]()
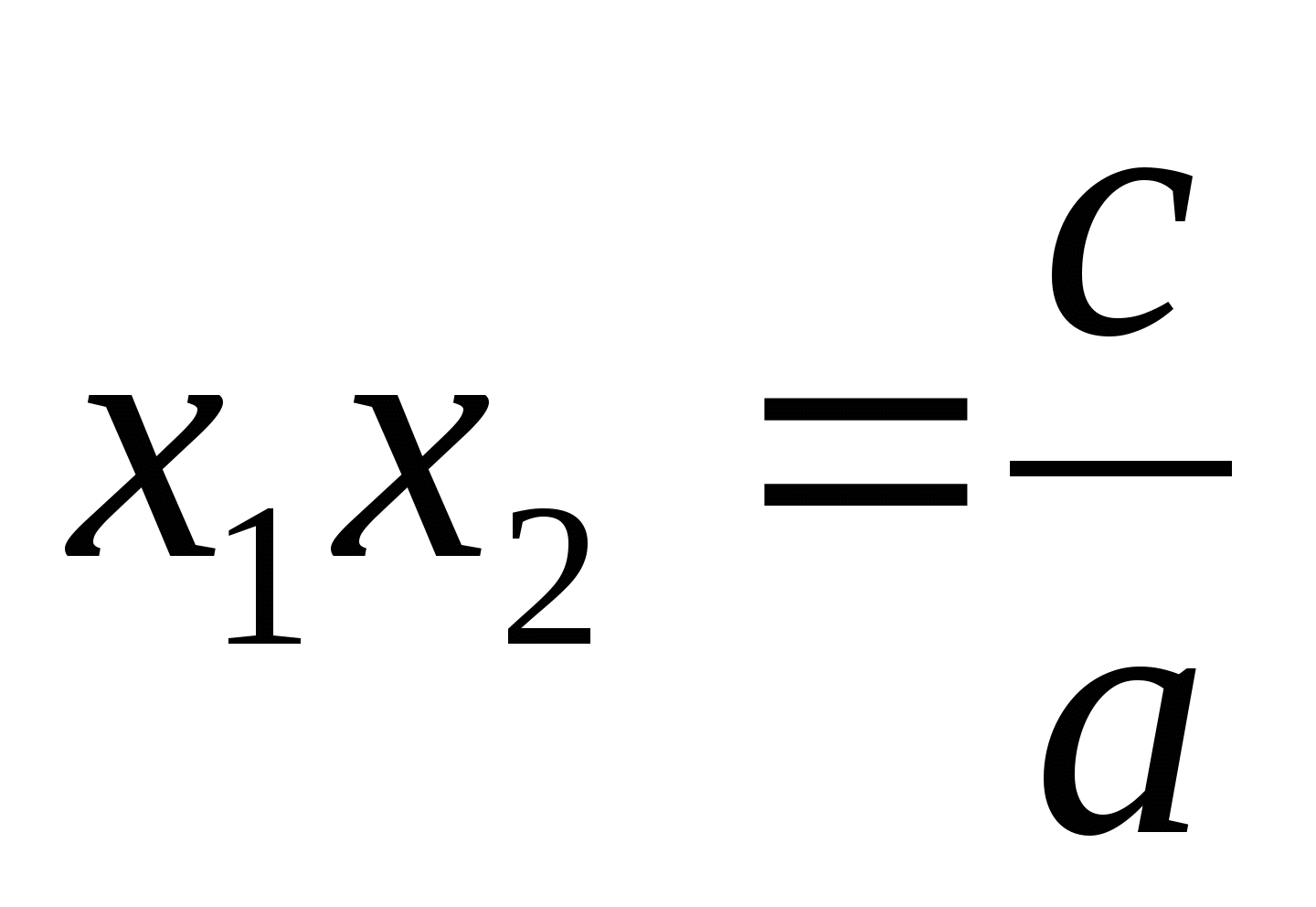 <
<
![]()
при этом положительный корень имеет большую абсолютную величину, если
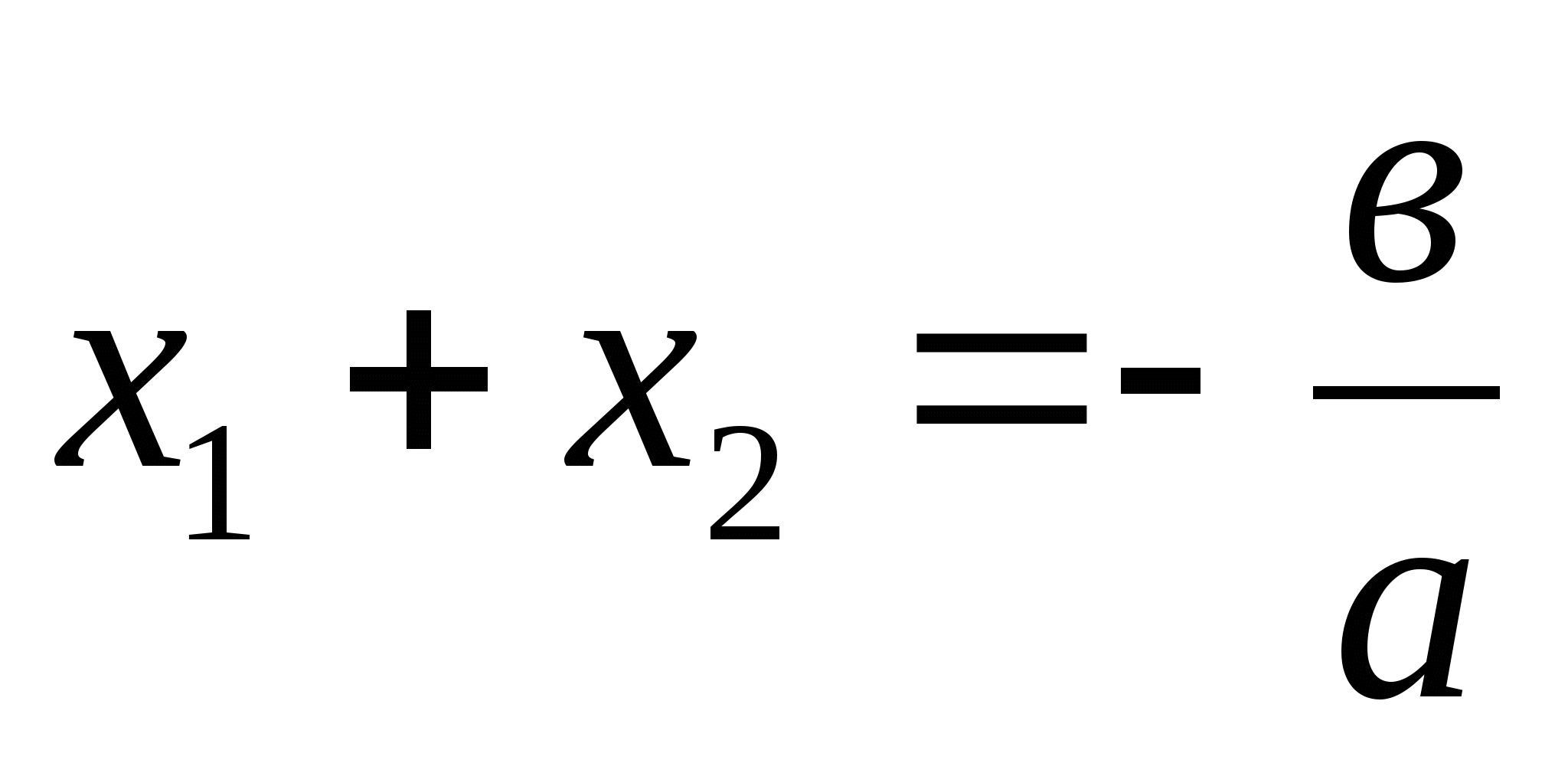 >
>
![]()
если же
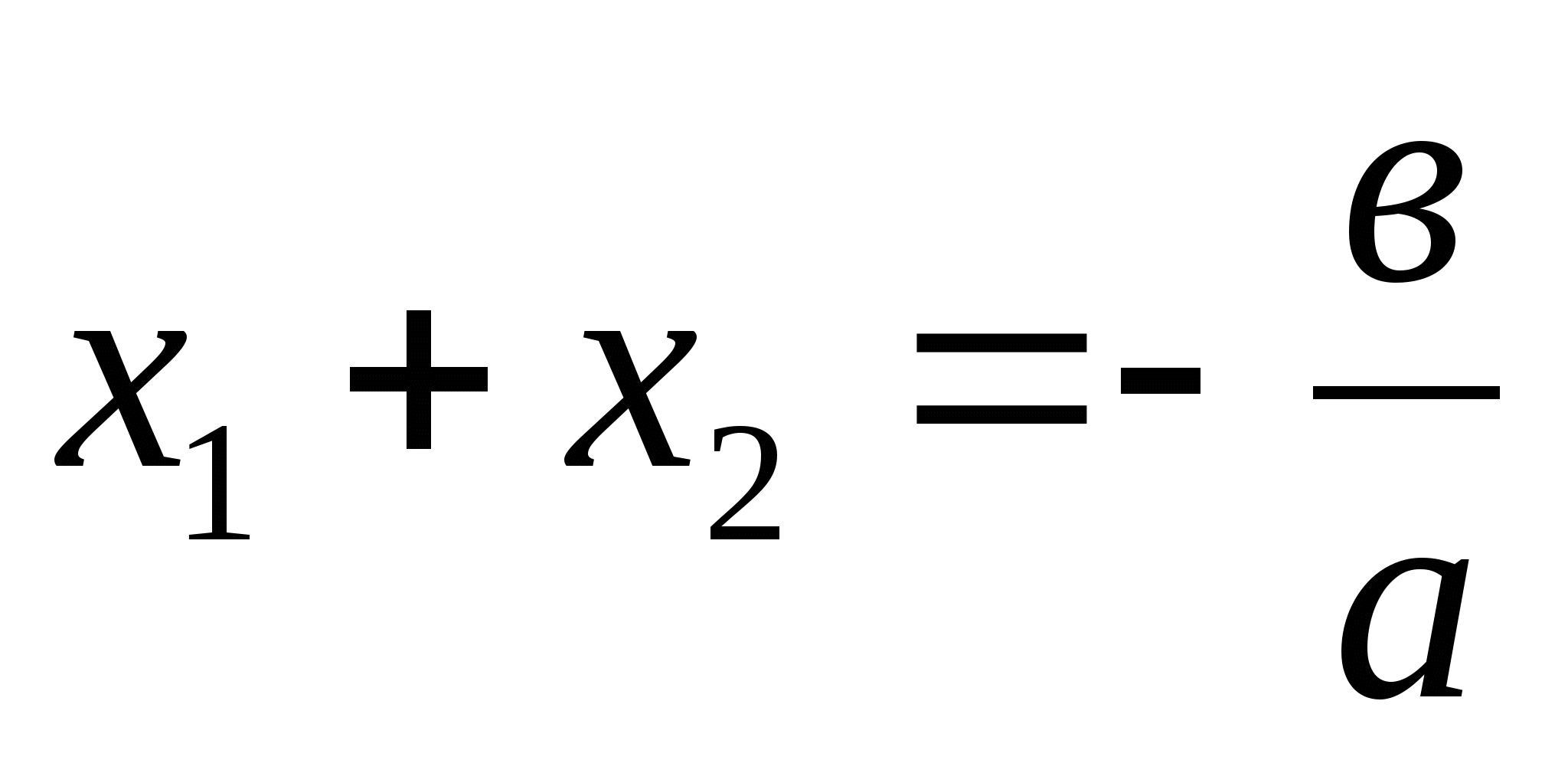 <
<
![]()
то отрицательный корень имеет большую абсолютную величину.
Задания для самостоятельного решения
-
При каких значениях
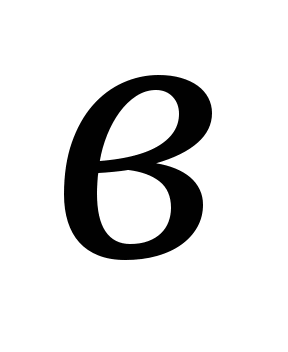 уравнение
уравнение
![]()
имеет два различных положительных корня?
-
При каких значениях
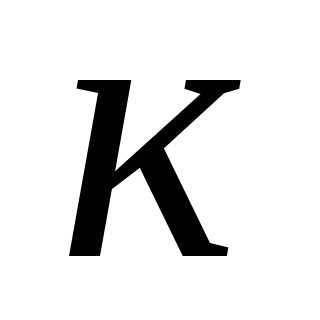 уравнение
уравнение
![]()
имеет корни разных знаков?
-
При каком значении
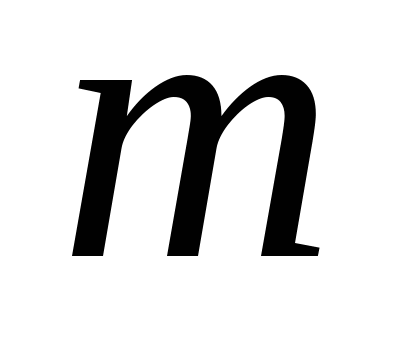 сумма квадратов корней уравнения
сумма квадратов корней уравнения
![]()
минимальна?
-
При каком значении
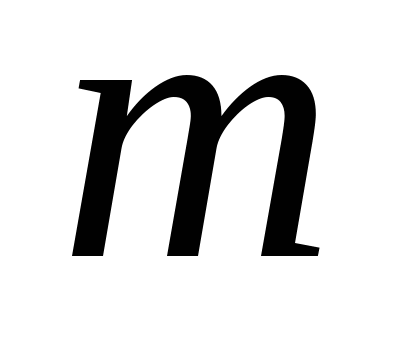 сумма квадратов корней уравнения
сумма квадратов корней уравнения
![]()
минимальна?
-
При каком значении
 корни уравнения
корни уравнения
![]()
таковы, что сумма их квадратов равна ![]() ?
?
-
При каком значении
 сумма квадратов корней уравнения
сумма квадратов корней уравнения
![]()
минимальна?
-
При каких значениях
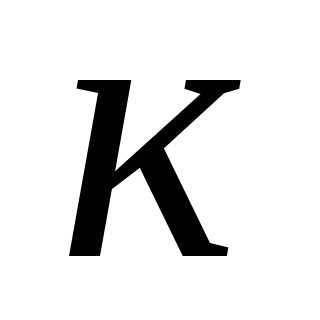 произведение корней квадратного уравнения
произведение корней квадратного уравнения
![]()
равно нулю?
-
При каких значениях
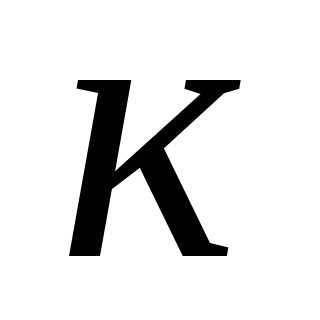 сумма корней квадратного уравнения
сумма корней квадратного уравнения
![]()
равна нулю?
-
В уравнении
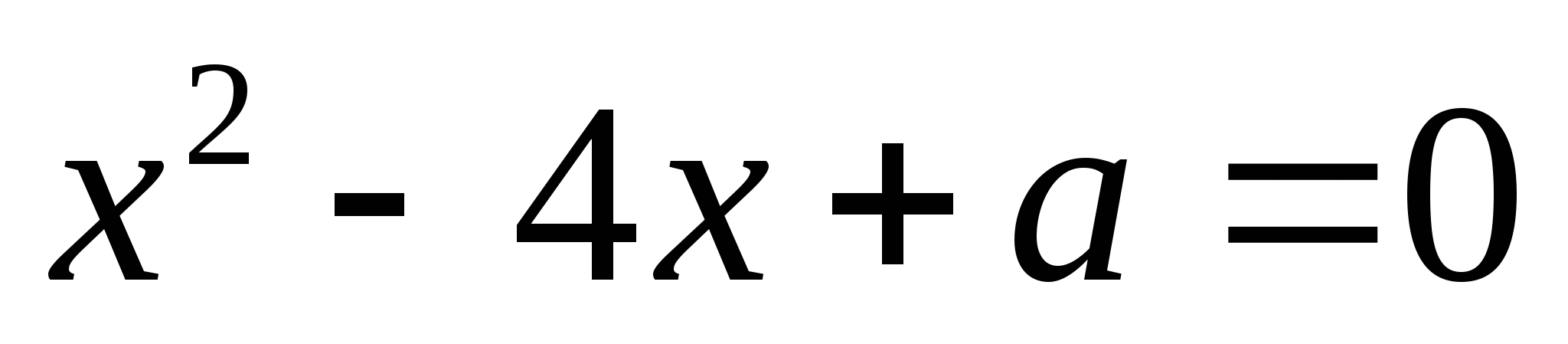 сумма квадратов корней равна 16. Найдите
сумма квадратов корней равна 16. Найдите  .
.
-
В уравнении

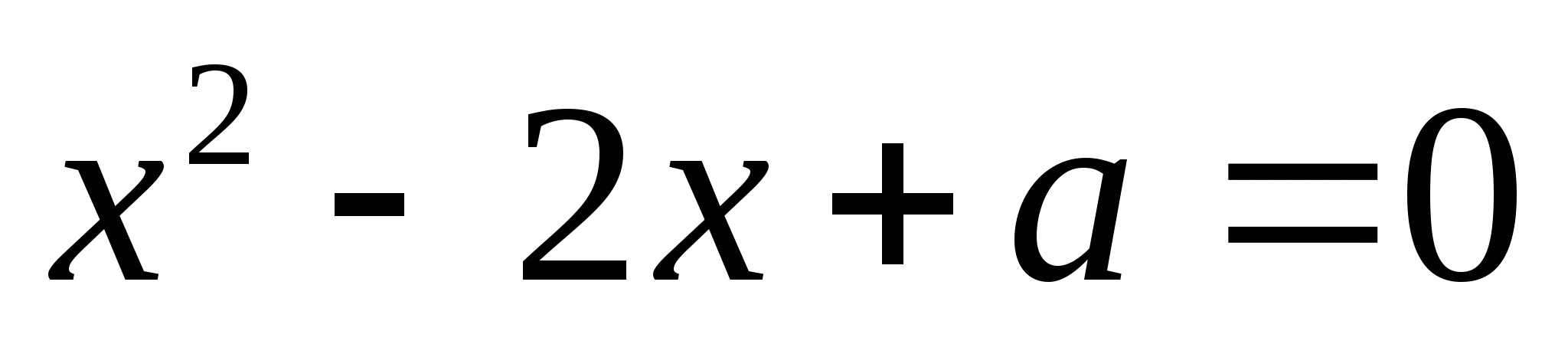 квадрат разности корней равен 16. Найдите
квадрат разности корней равен 16. Найдите  .
.
-
При каких значениях
 сумма корней уравнения
сумма корней уравнения
![]()
равна сумме квадратов его корней?
-
При каком значении параметра
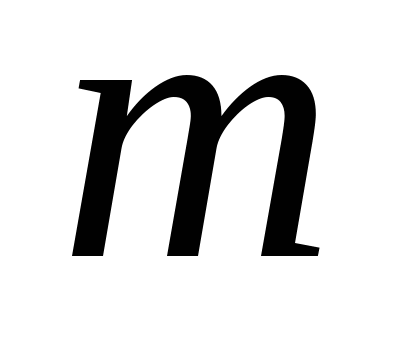 сумма квадратов корней уравнения
сумма квадратов корней уравнения
![]()
наибольшая?
-
При каких значениях
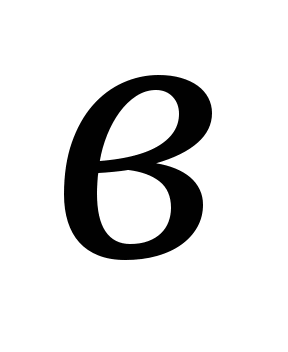 и
и 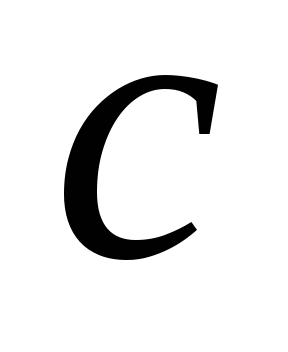 корни уравнения
корни уравнения
![]()
равны ![]() и
и ![]()
-
При каких значениях параметра
 один из корней квадратного уравнения
один из корней квадратного уравнения
![]()
в два раза больше другого?
-
Известно, что корни уравнения
![]()
на 1 меньше корней уравнения
![]() .
.
Найдите ![]() и корни каждого из уравнений.
и корни каждого из уравнений.
-
Известно, что корни уравнения
![]()
равны соответственно квадратам корней уравнения
![]() .
.
Найдите ![]() и
и ![]() , и корни каждого из уравнений.
, и корни каждого из уравнений.
Ответы
№ 1. ![]() <
< ![]()
№ 2. ![]() <
< ![]() и
и ![]() >
> ![]()
№ 3. ![]() .
.
№ 4. 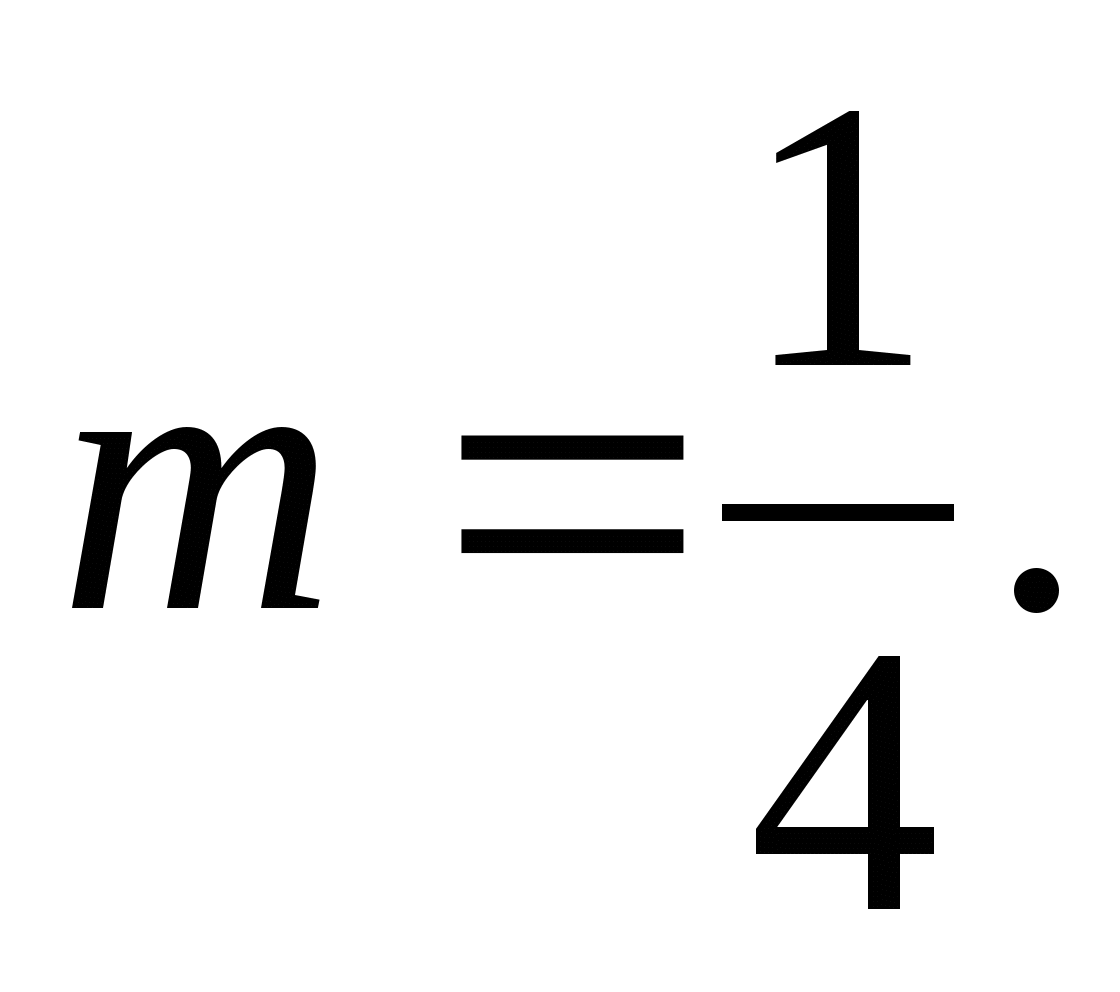
№ 5. ![]()
№ 6. ![]()
№ 7. 3;4.
№ 8. 1.
№ 9. 0.
№ 10. - 3.
№ 11. ![]()
№ 12. - 1.
№ 13. ![]() или
или ![]()
№ 14. 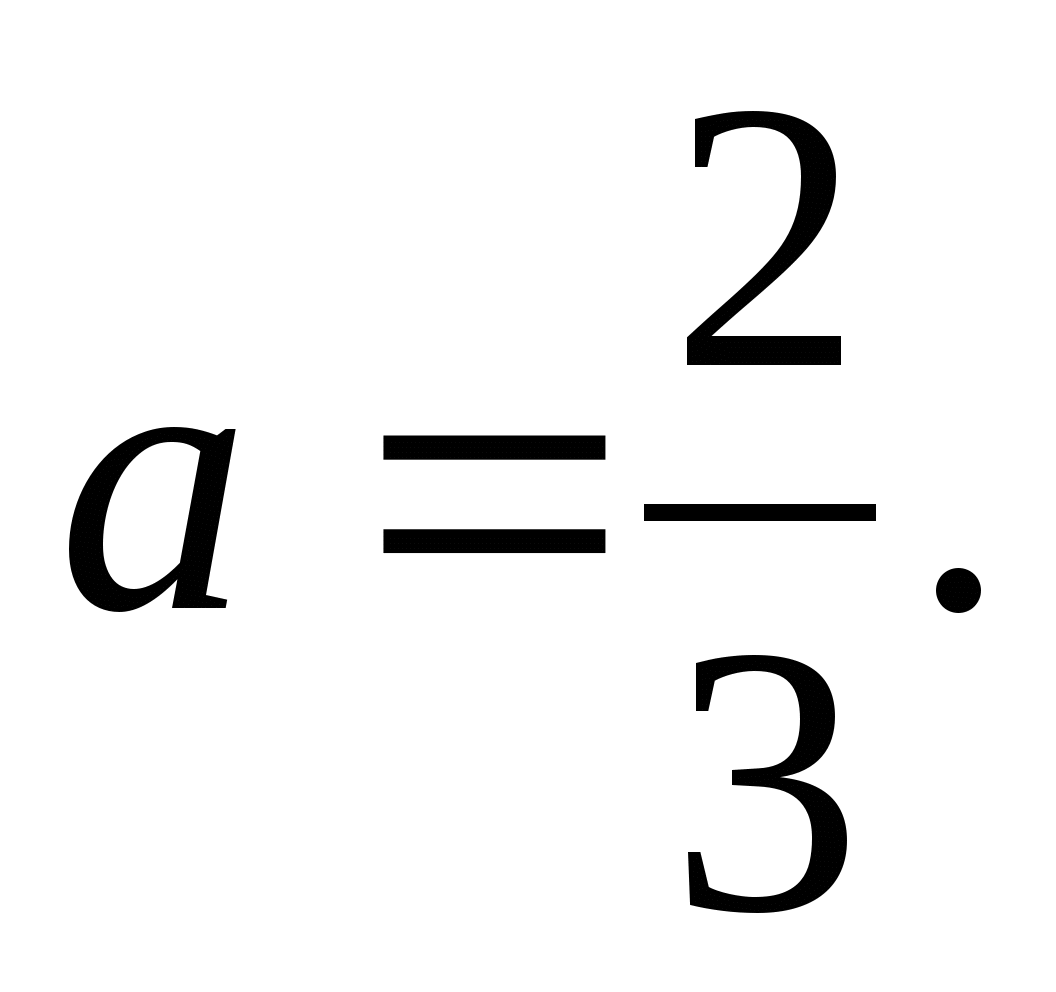
№ 15. ![]() 2 и 3 - корни первого уравнения, 3 и 4 - корни второго уравнения.
2 и 3 - корни первого уравнения, 3 и 4 - корни второго уравнения.
№ 16. ![]() корни первого уравнения равны 2; 3, корни второго уравнения равны
4; 9, или
корни первого уравнения равны 2; 3, корни второго уравнения равны
4; 9, или ![]() корни первого уравнения равны - 2; - 3, корни второго уравнения
равны 4; 9.
корни первого уравнения равны - 2; - 3, корни второго уравнения
равны 4; 9.
Теоремы о расположении корней квадратного трёхчлена на координатной прямой
Пусть квадратный трёхчлен ![]() имеет корни
имеет корни ![]() и
и ![]() , а
, а ![]() - некоторое действительное число. Во всех нижеперечисленных
соотношениях
- некоторое действительное число. Во всех нижеперечисленных
соотношениях ![]() представляет собой выражение
представляет собой выражение ![]()
Теорема 1. Для того чтобы оба корня квадратного
трёхчлена были меньше, чем число ![]() , т.е. лежали на координатной прямой левее точки
, т.е. лежали на координатной прямой левее точки ![]() , необходимо и достаточно выполнения следующих условий:
, необходимо и достаточно выполнения следующих условий:
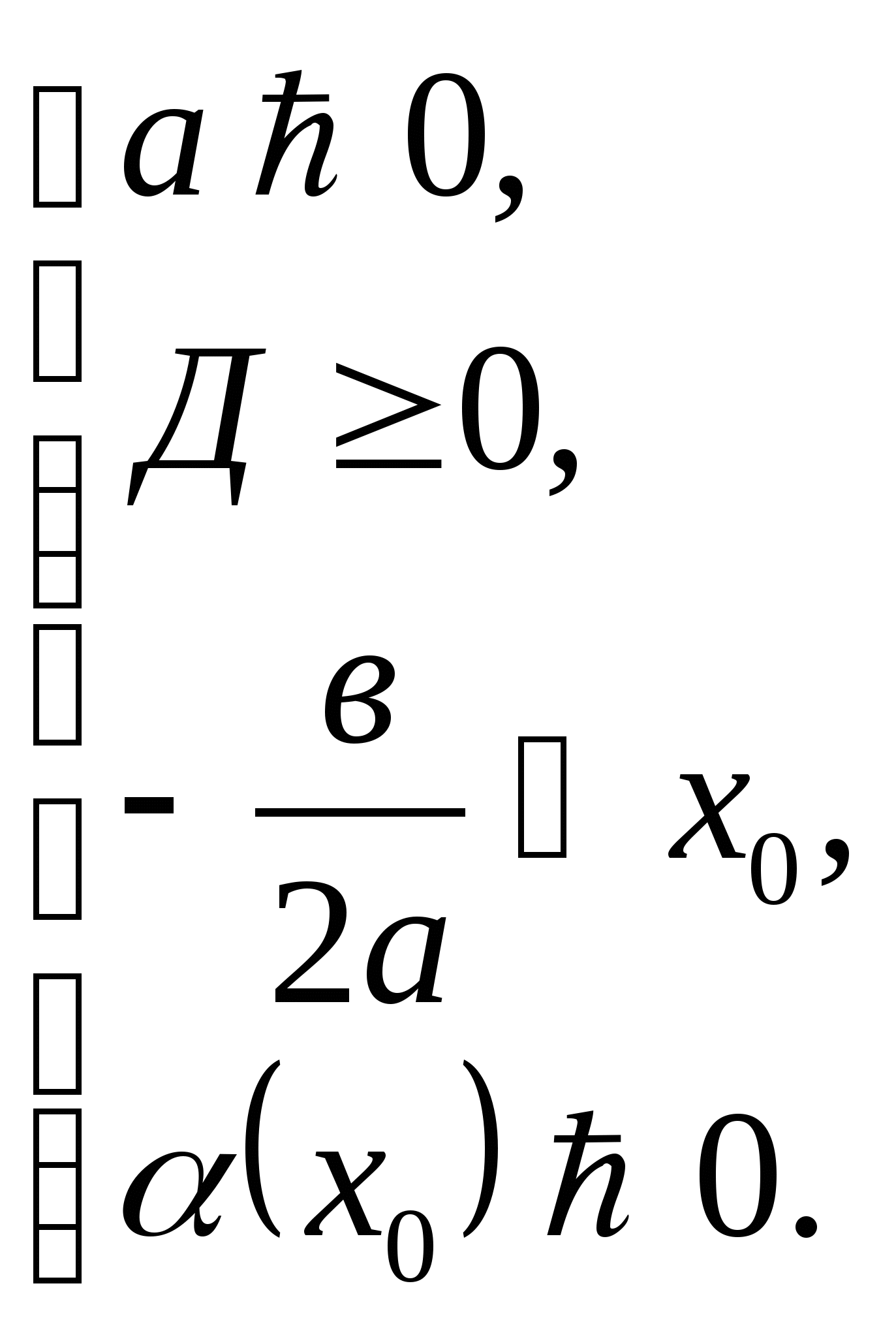
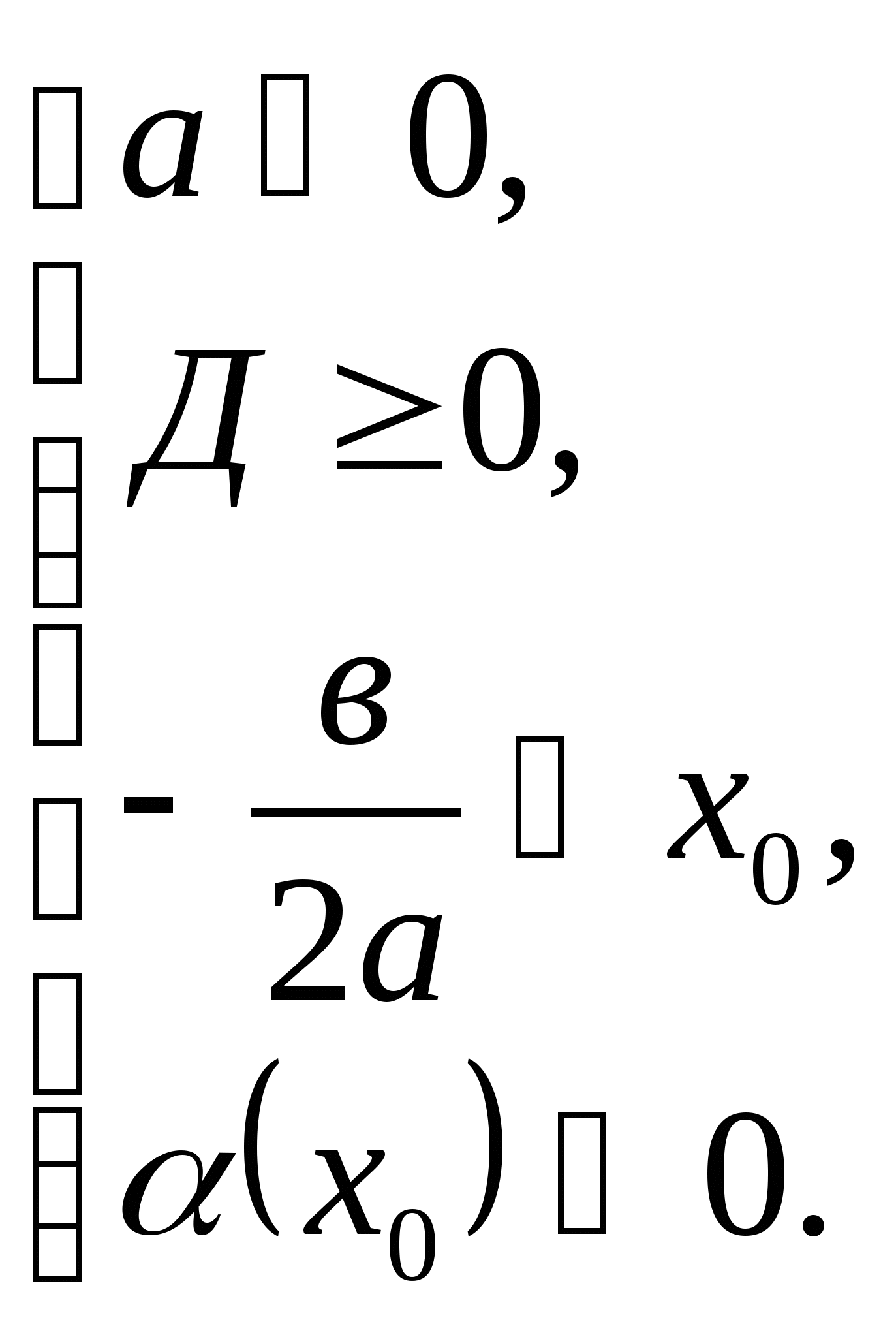
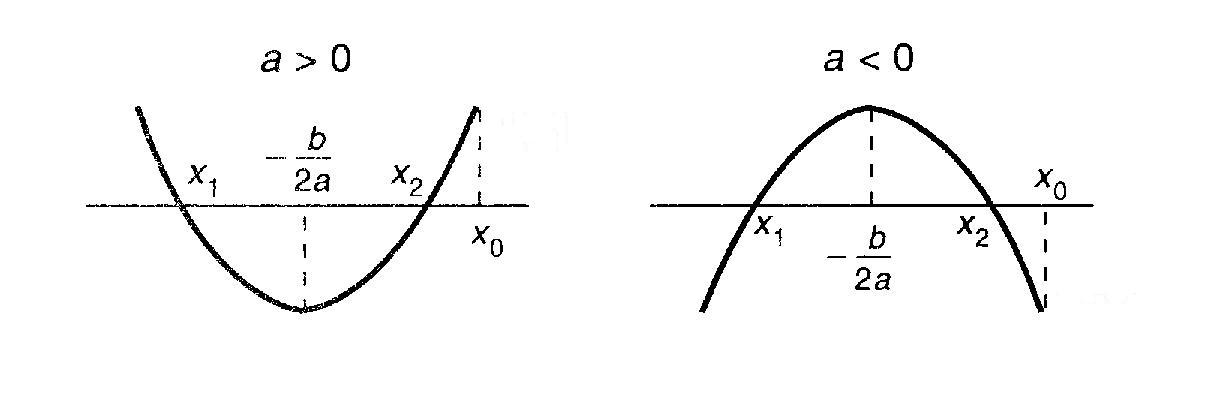
Теорема 2. Чтобы один из корней квадратного
трёхчлена был меньше, чем число ![]() , а другой больше числа
, а другой больше числа ![]() , т.е. точка
, т.е. точка ![]() лежала бы между корнями, необходимо и достаточно выполнения
следующих условий:
лежала бы между корнями, необходимо и достаточно выполнения
следующих условий:
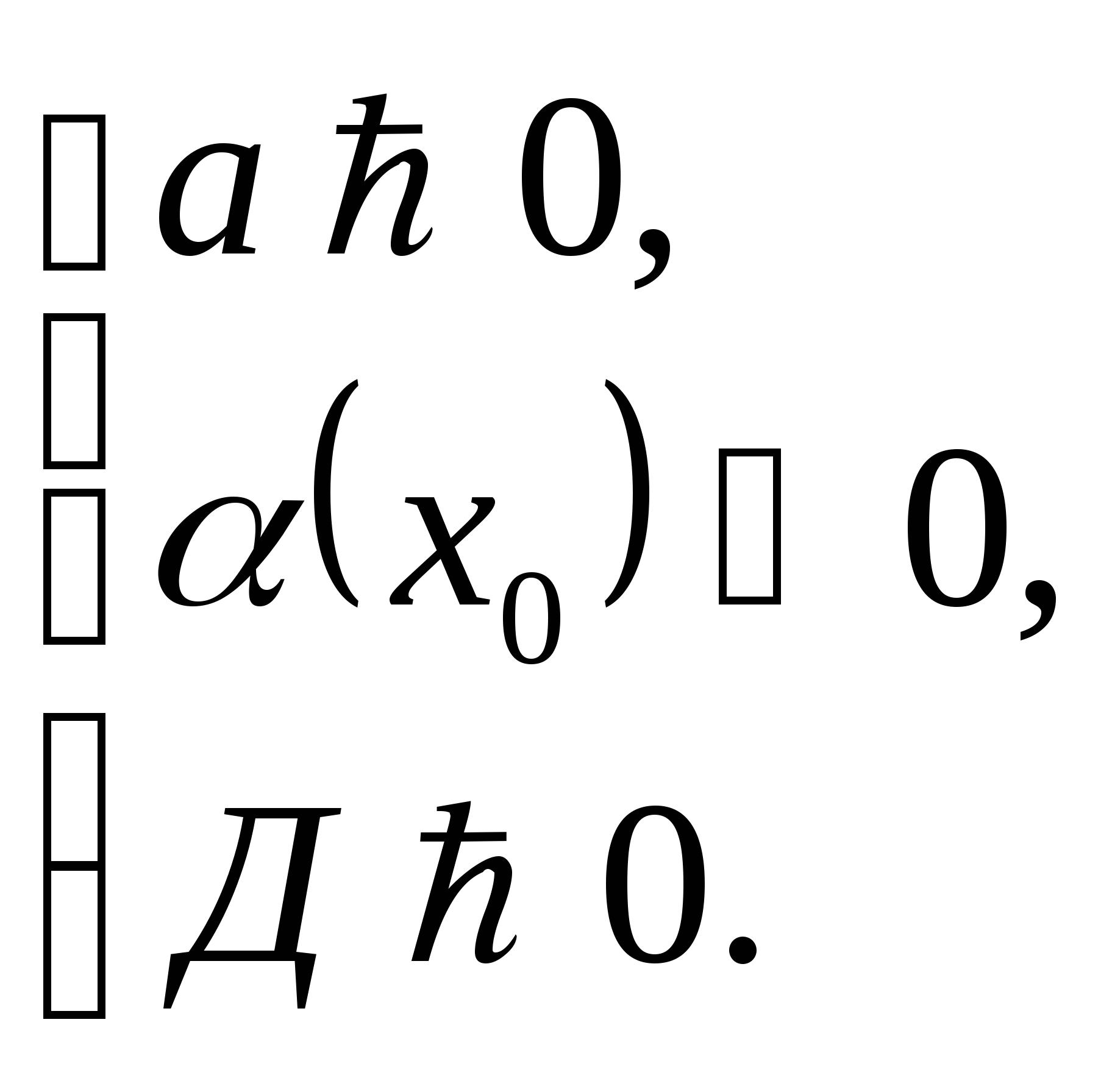
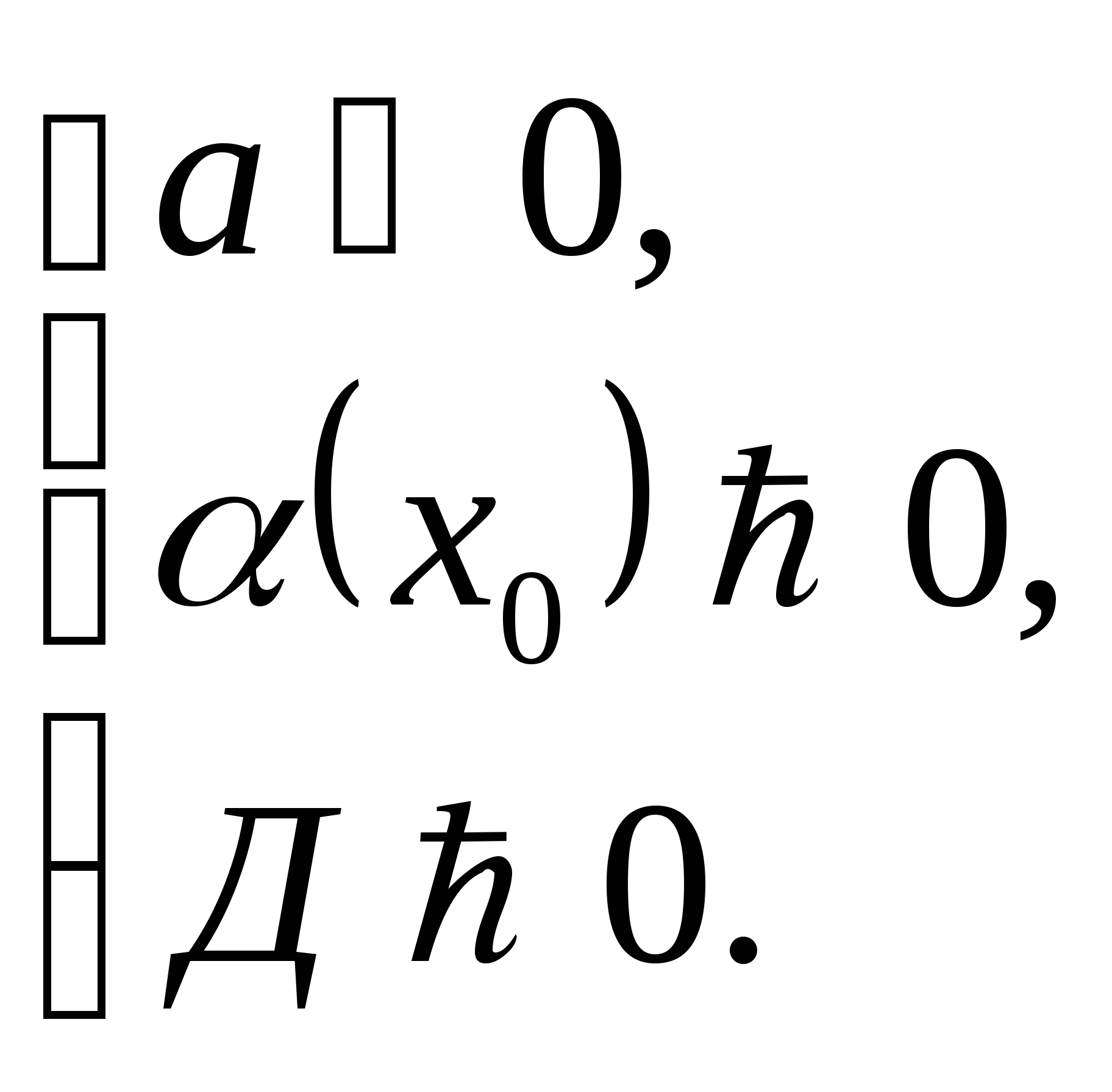
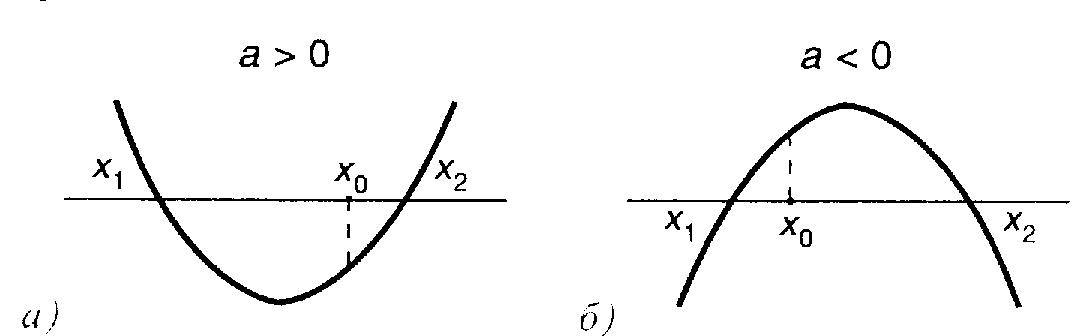
Теорема 3. Чтобы оба корня квадратного трёхчлена
были больше, чем число ![]() ,т.е. лежали на координатной прямой правее, чем точка
,т.е. лежали на координатной прямой правее, чем точка ![]() , необходимо и достаточно выполнения следующих условий:
, необходимо и достаточно выполнения следующих условий:
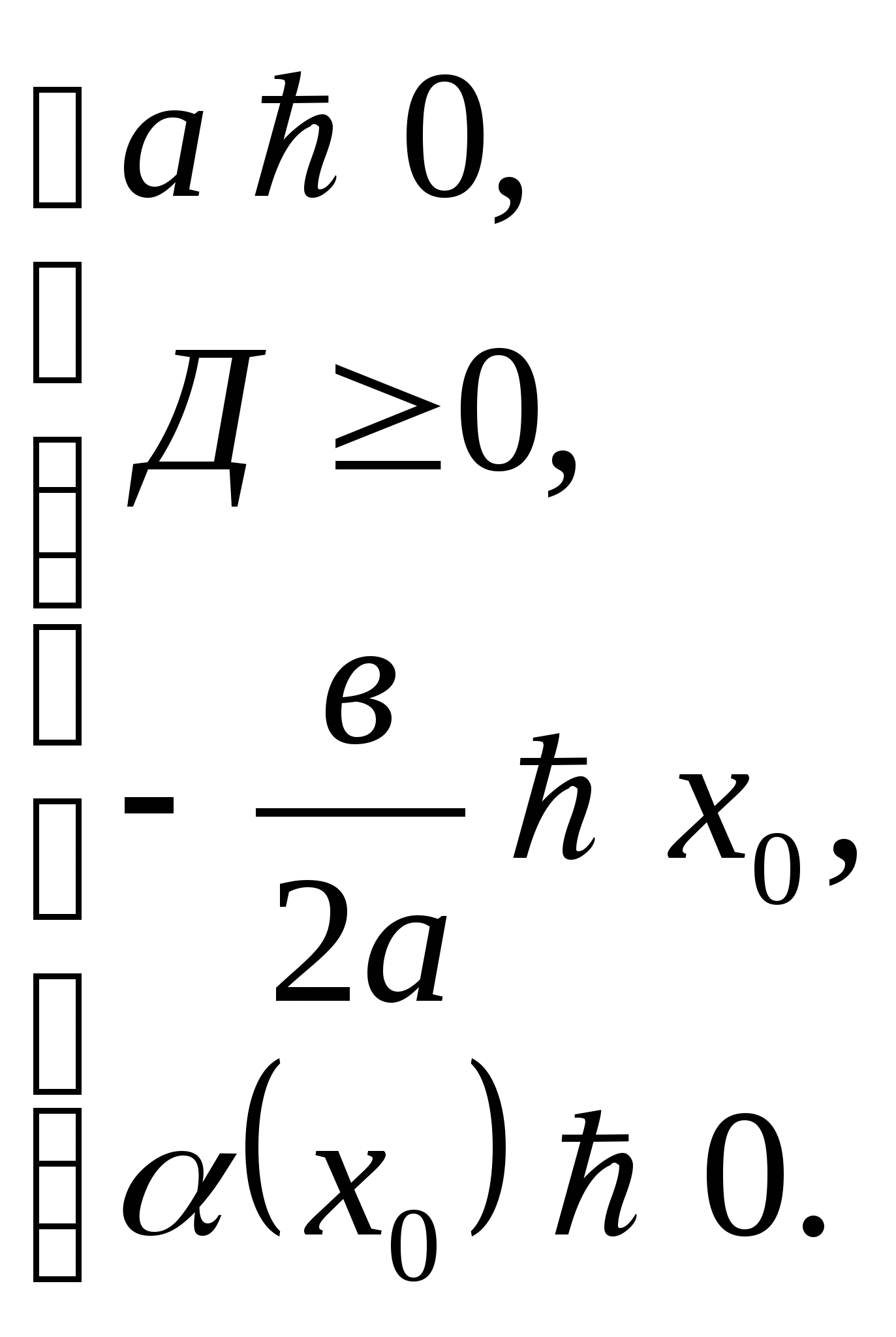
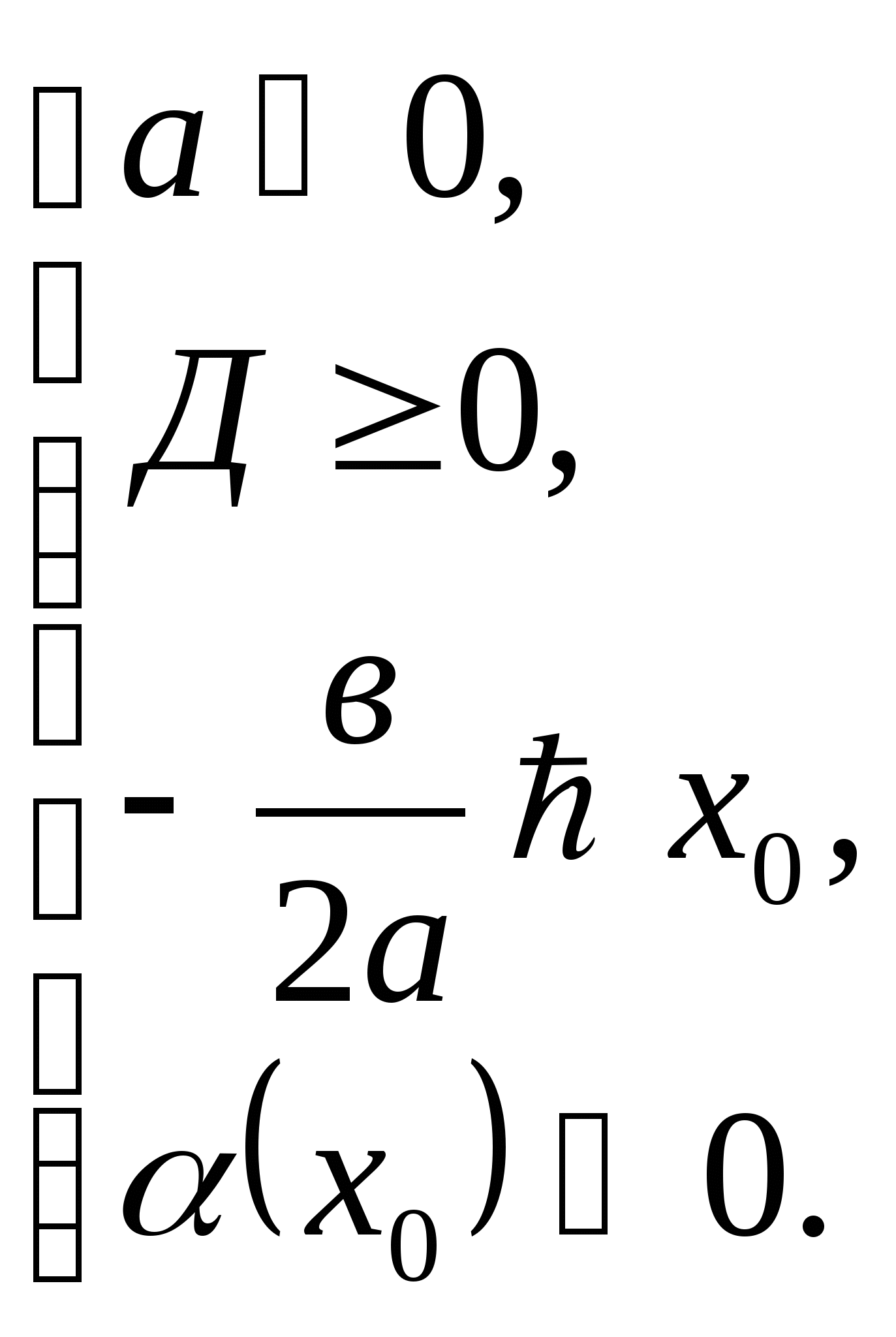
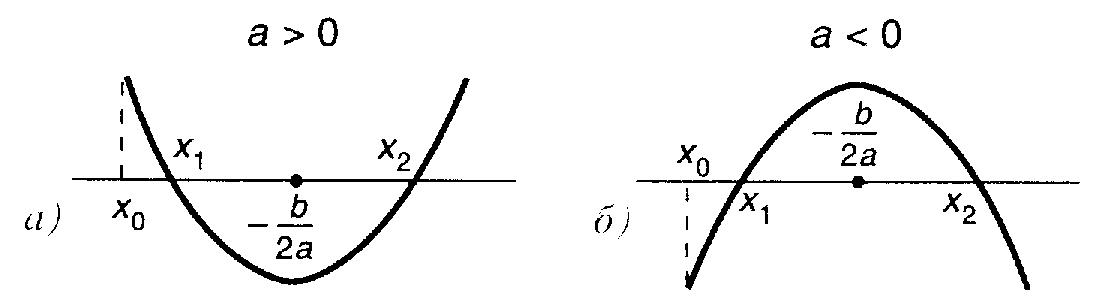
![]() Следствие
1. Чтобы оба корня квадратного трёхчлена были больше,
Следствие
1. Чтобы оба корня квадратного трёхчлена были больше,
чем число М, но меньше, чем число А (М < А), т.е. лежали в интервале между М и А, необходимо и достаточно:
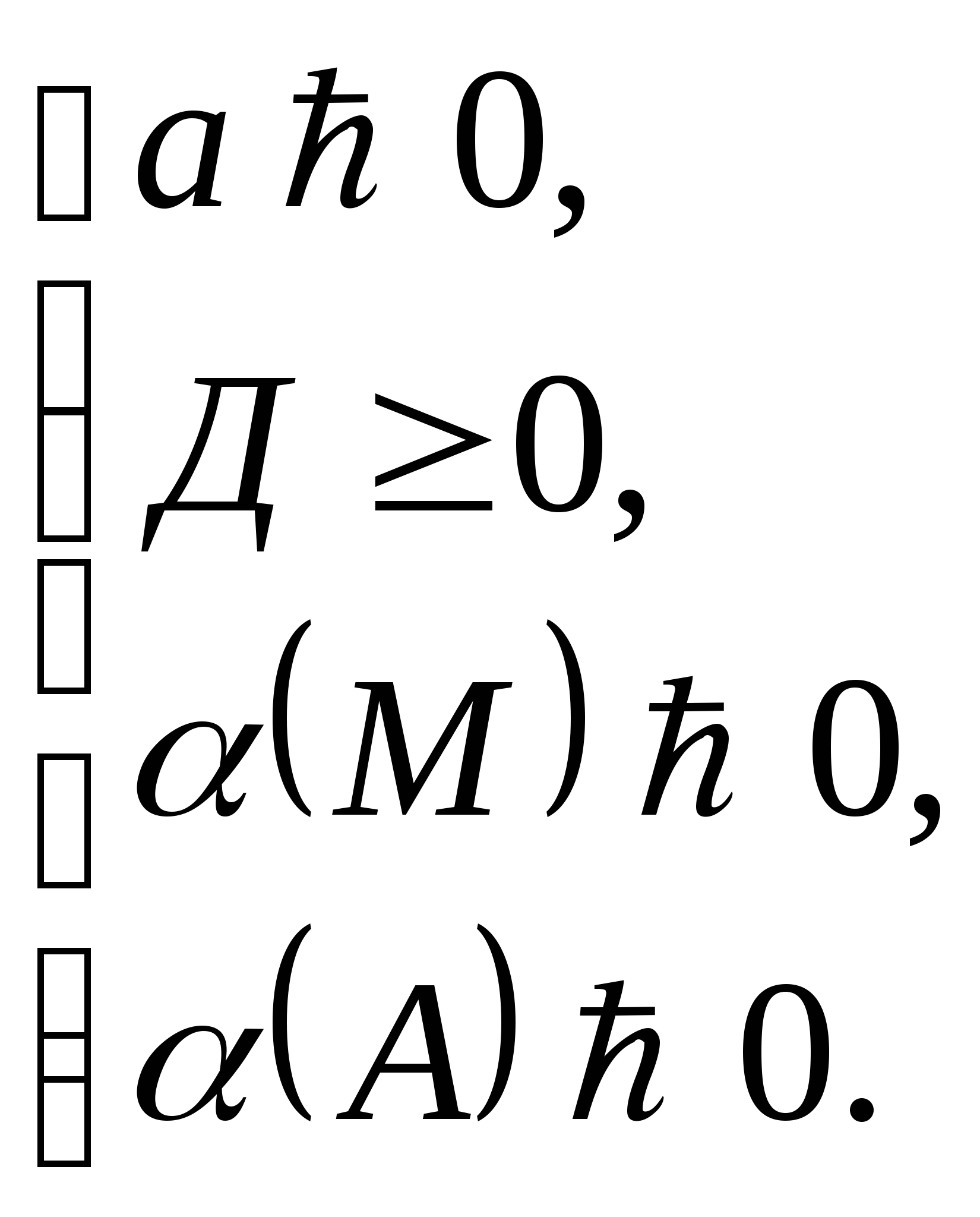
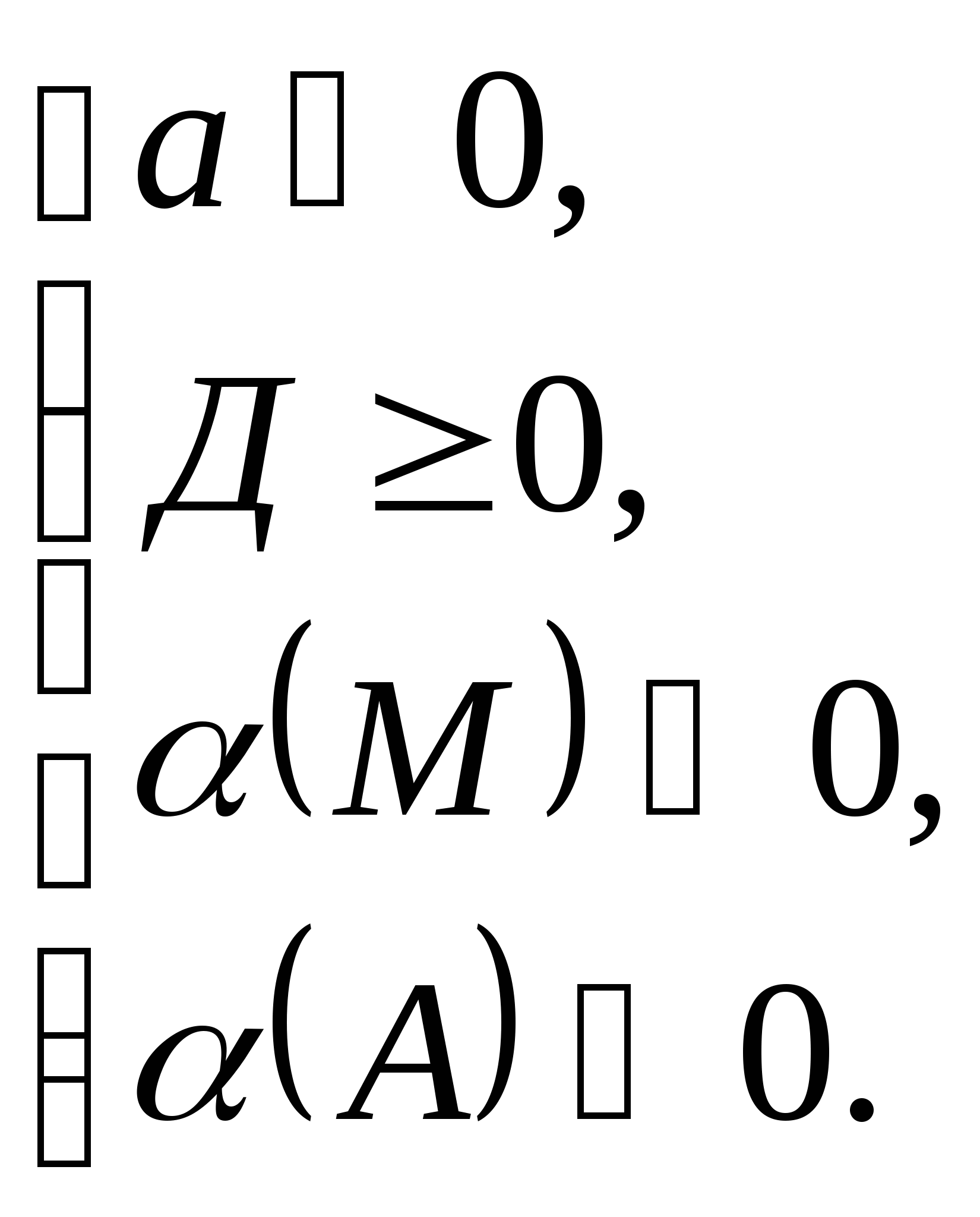
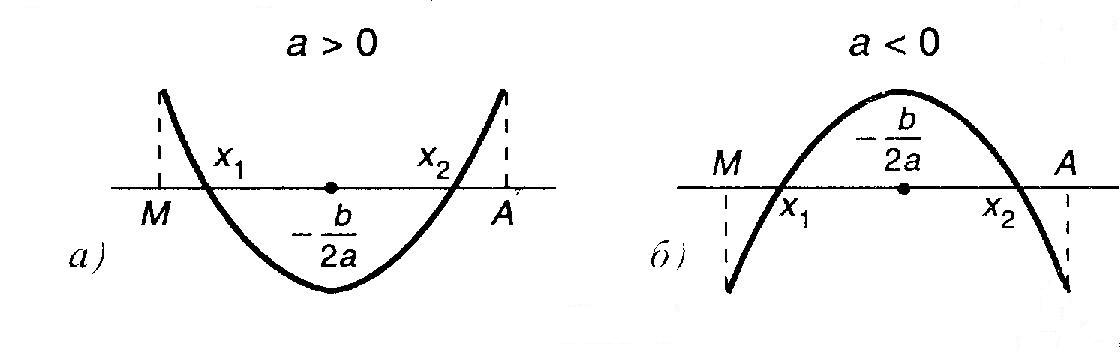
Следствие 2. Чтобы только больший корень квадратного трёхчлена лежал в интервале между М и А (М < А), необходимо и достаточно:
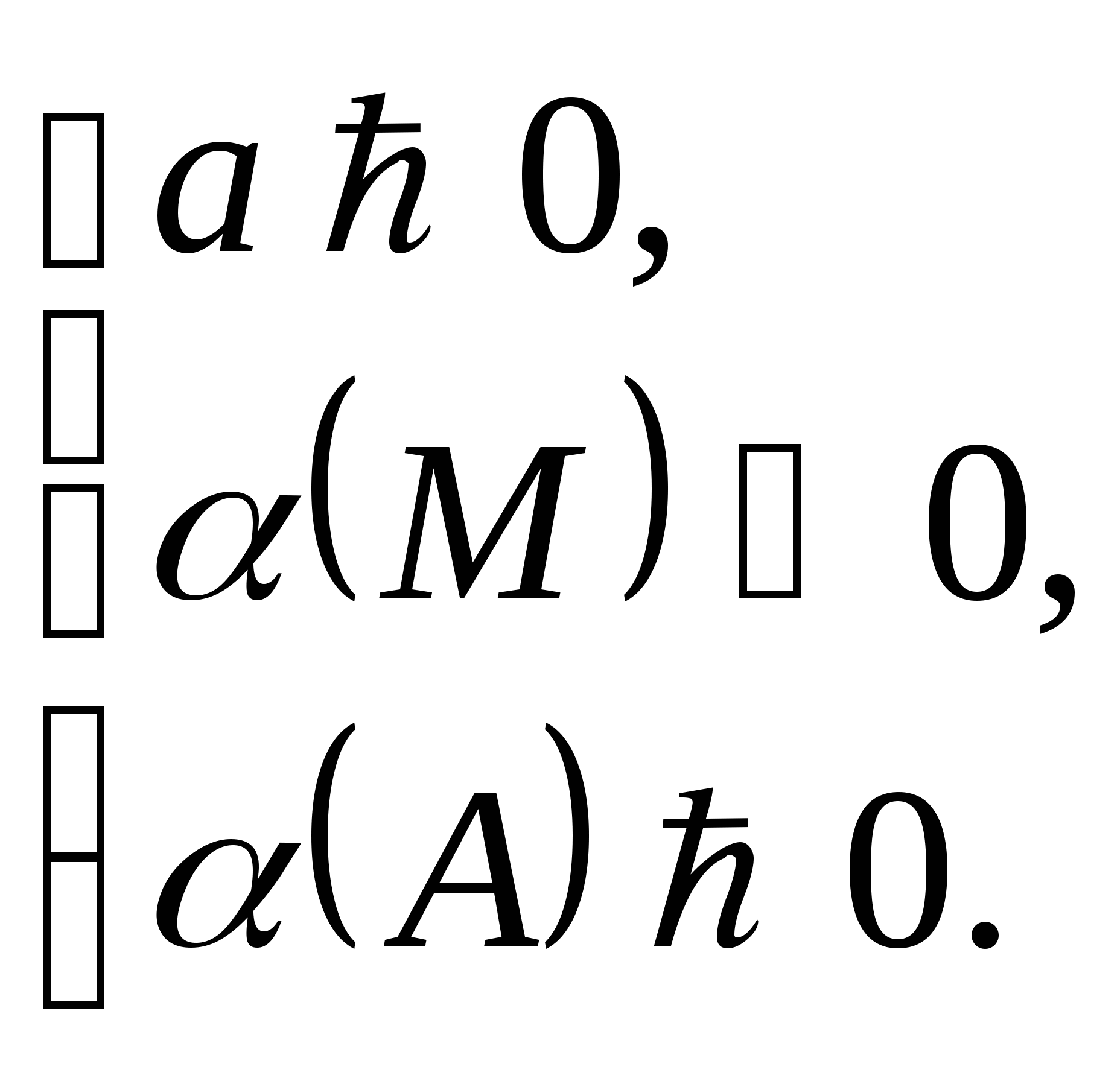
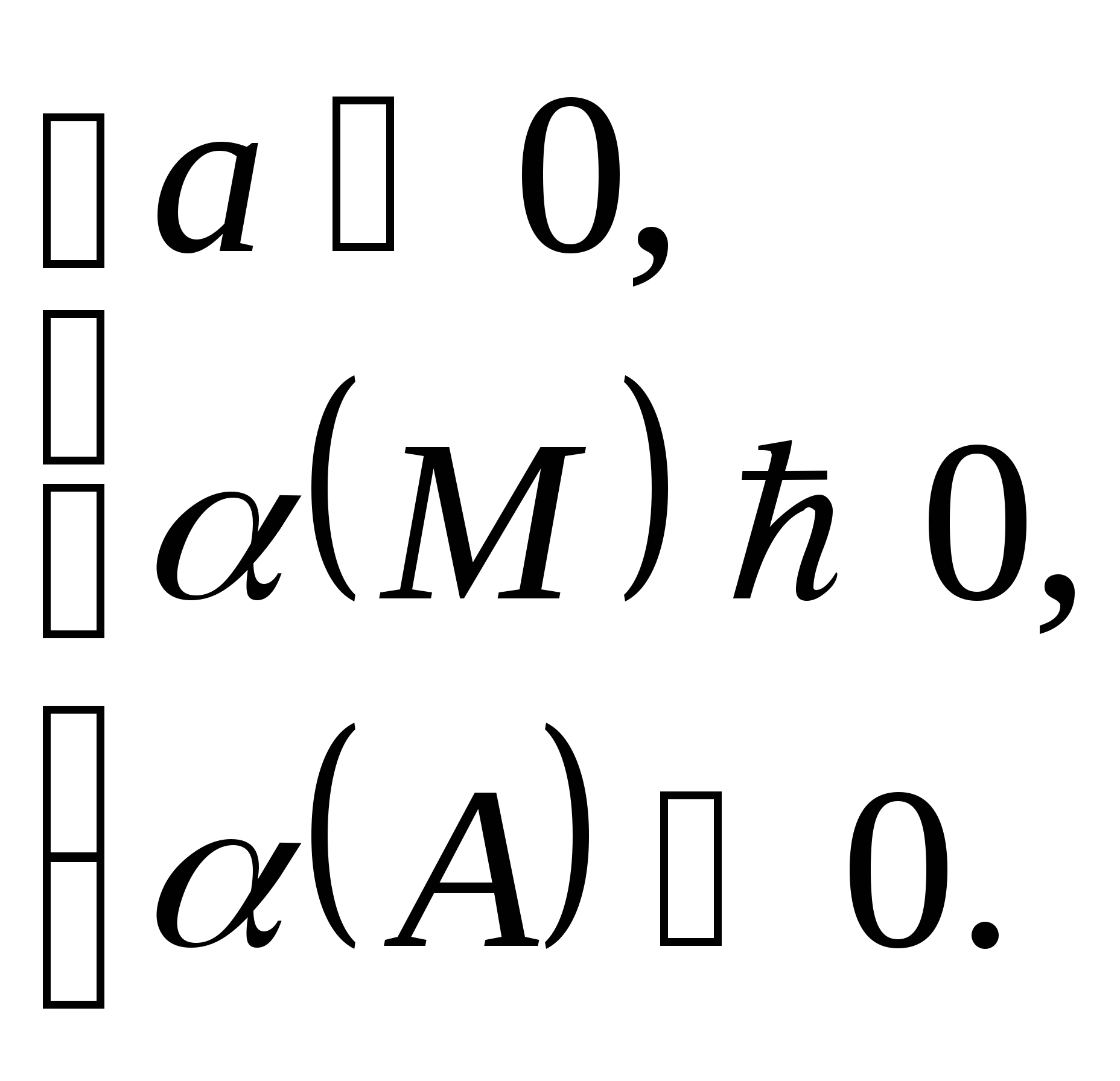
При этом меньший корень лежит вне отрезка МА.
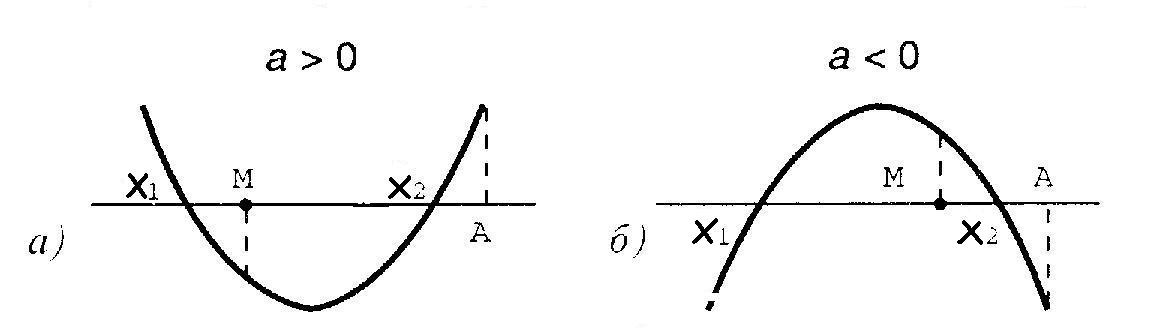
Следствие 3. Чтобы только меньший корень квадратного трёхчлена лежал в интервале между М и А (М < А), необходимо и достаточно:
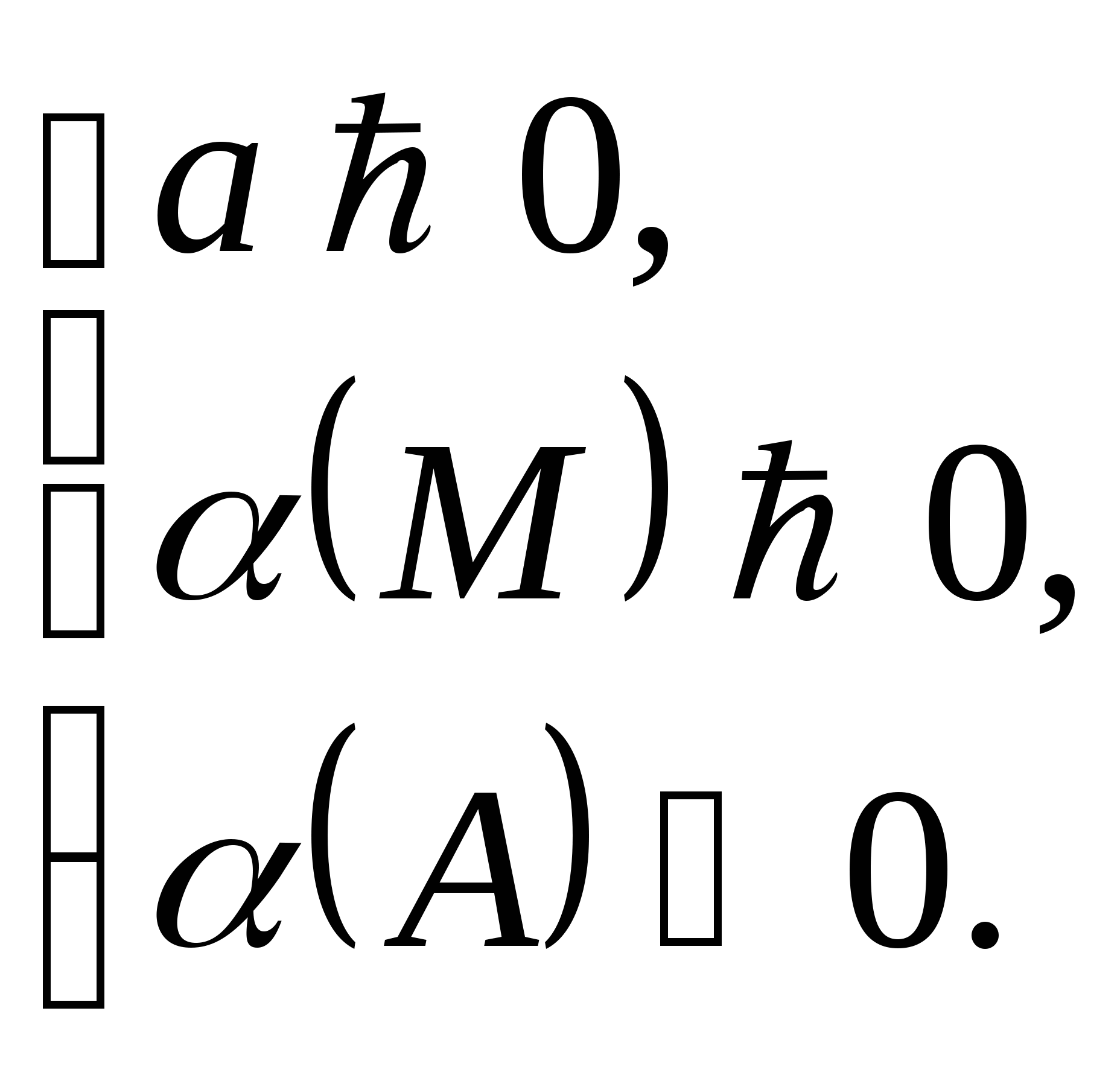
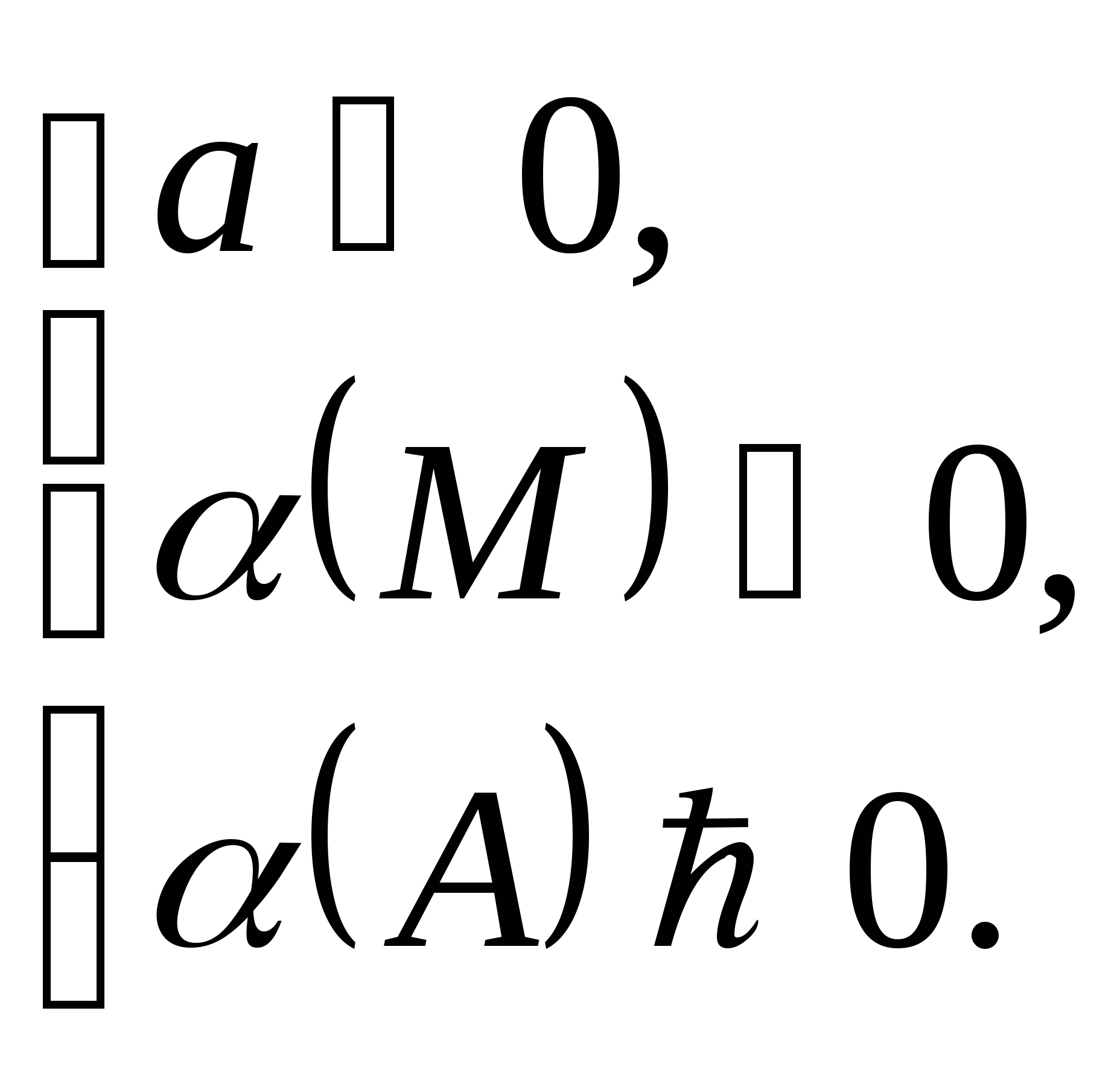
При этом больший корень лежит вне отрезка МА.
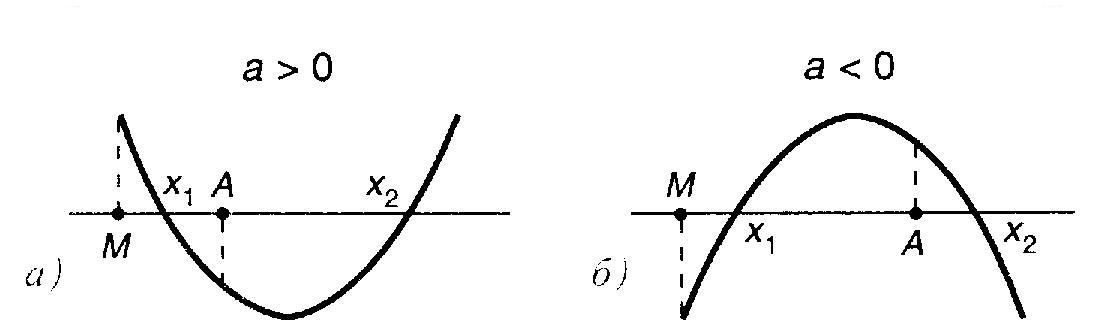
Следствие 4. Чтобы один корень квадратного трёхчлена был меньше, чем М, а другой больше, чем А (М < А), т.е. отрезок МА целиком лежал внутри интервала между корнями, необходимо и достаточно:
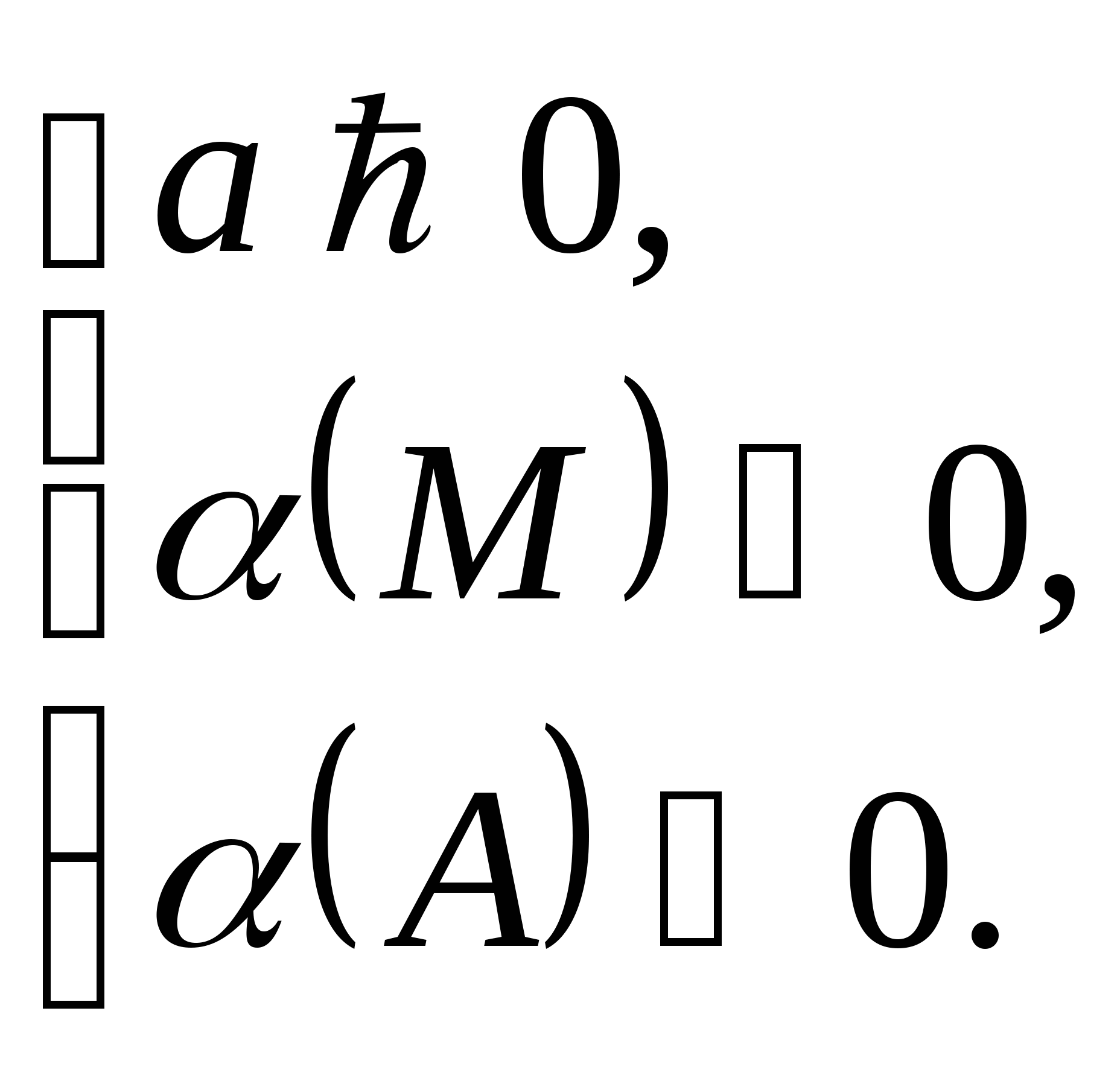
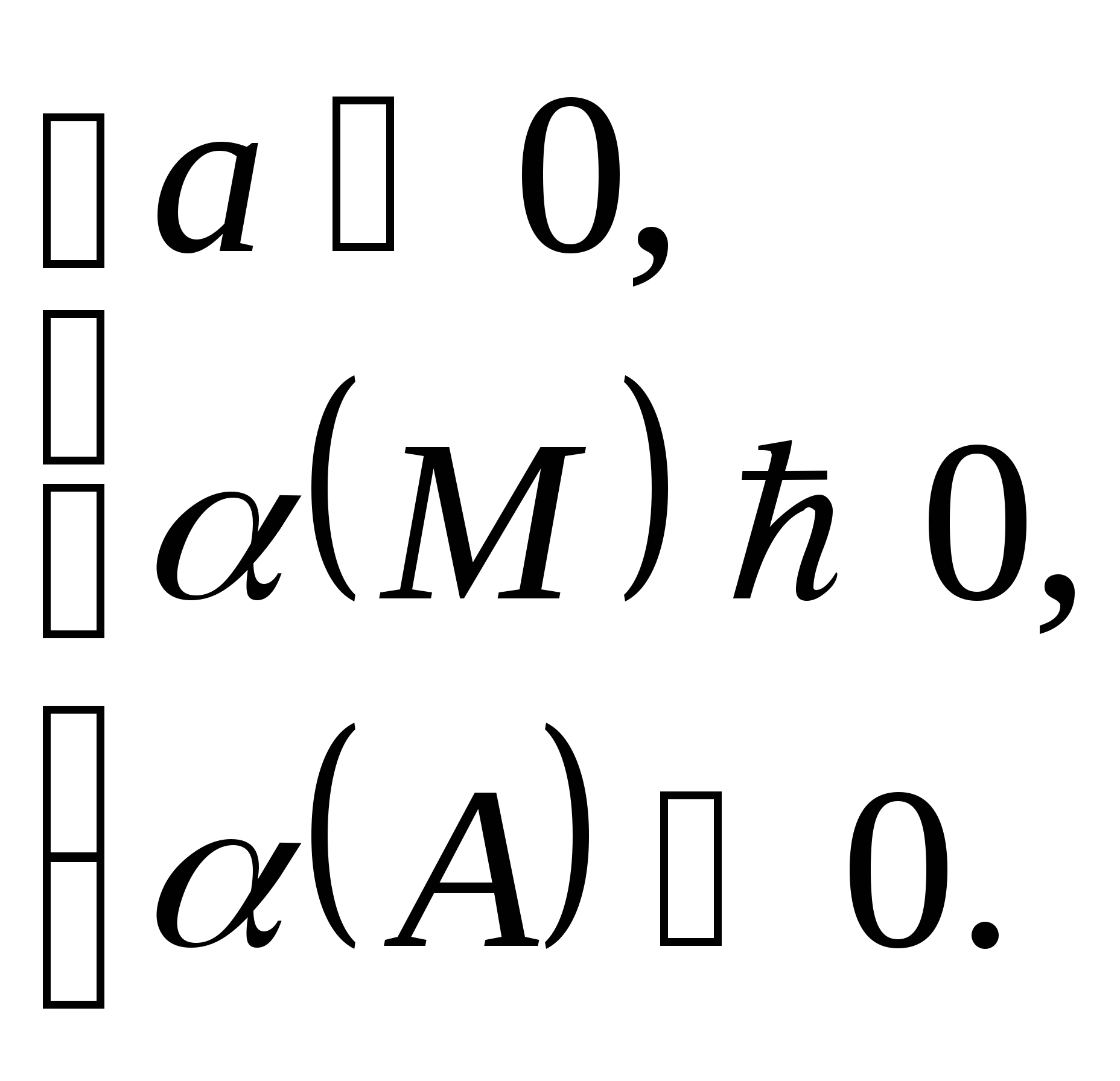
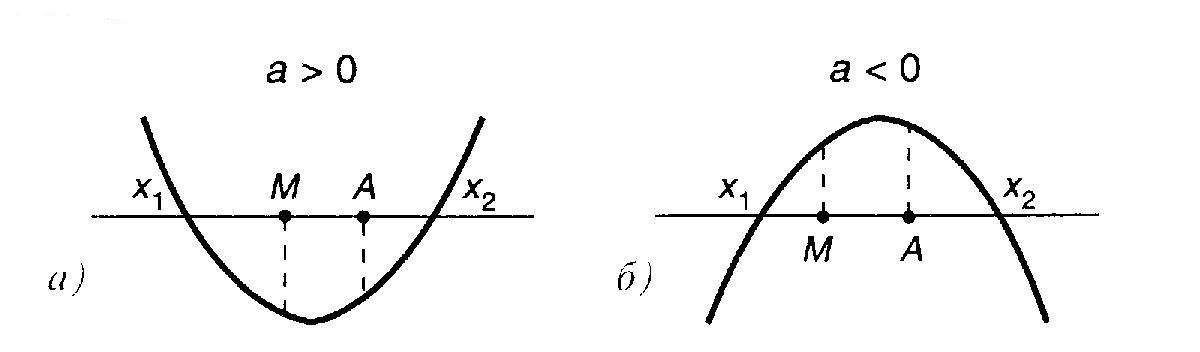
Задания для самостоятельного решения
-
При каких значениях
 оба корня квадратного трёхчлена
оба корня квадратного трёхчлена
![]()
больше ![]() ?
?
-
При каких значениях
 оба корня квадратного уравнения
оба корня квадратного уравнения
![]()
больше 3?
-
При каких значениях
 оба корня квадратного уравнения
оба корня квадратного уравнения
![]()
меньше - 1?
-
При каких значениях
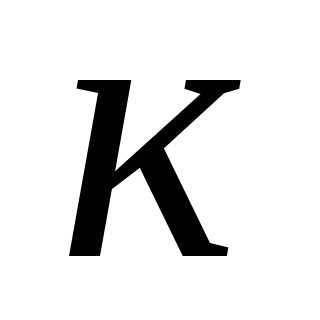 оба корня квадратного уравнения
оба корня квадратного уравнения
![]()
больше 1?
-
При каких значениях
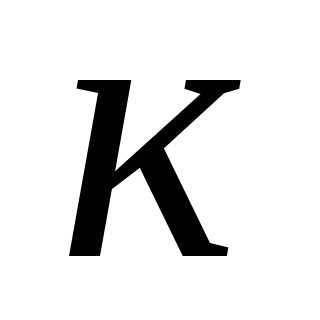 один из корней квадратного уравнения
один из корней квадратного уравнения
![]()
больше 1, а другой меньше 1?
-
При каких значениях
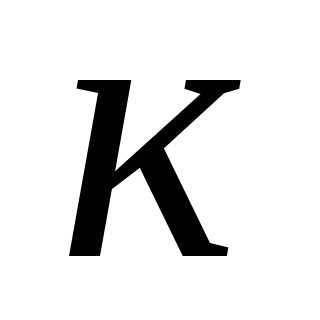 оба корня квадратного уравнения
оба корня квадратного уравнения
![]()
по абсолютной величине меньше 1?
-
При каких значениях
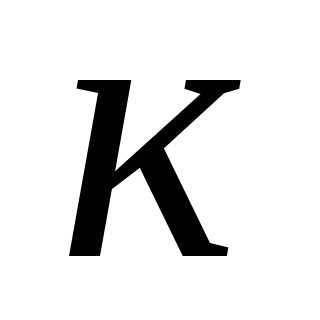 уравнение
уравнение
![]()
имеет один корень больше 3, а другой меньше 2?
-
При каких значениях
 корни уравнения
корни уравнения
![]()
принадлежат промежутку ![]() ?
?
-
При каких значениях
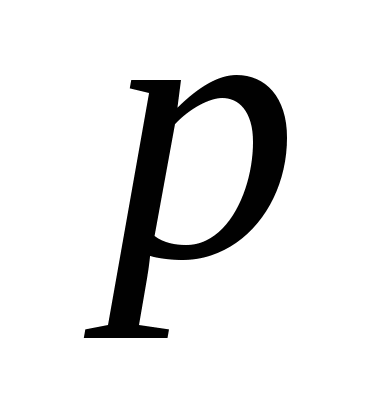 корни уравнения
корни уравнения
![]()
принадлежат промежутку ![]() ?
?
-
При каких значениях
 один корень квадратного уравнения
один корень квадратного уравнения
![]()
больше ![]() а другой меньше
а другой меньше ![]()
-
При каких значениях
 число
число 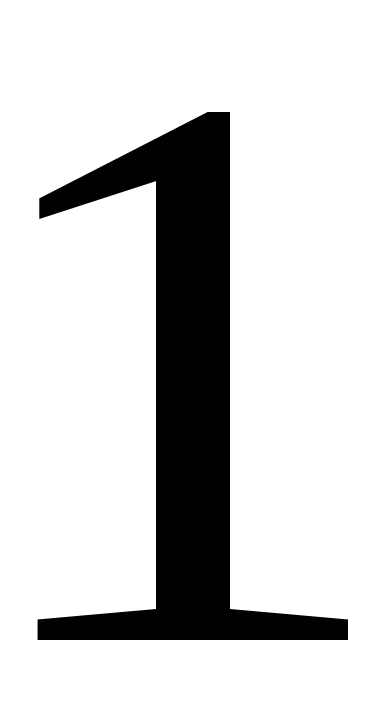 находится между корнями квадратного трёхчлена
находится между корнями квадратного трёхчлена
![]() ?
?
Ответы
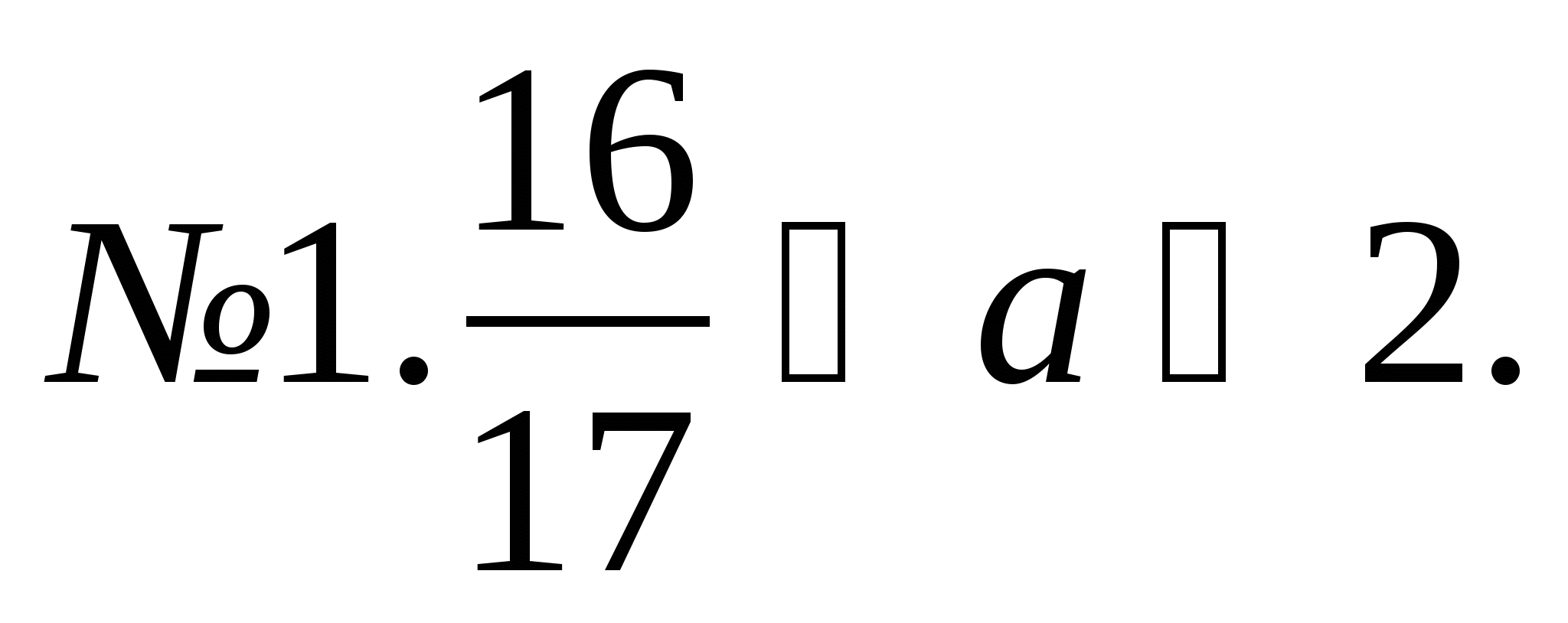
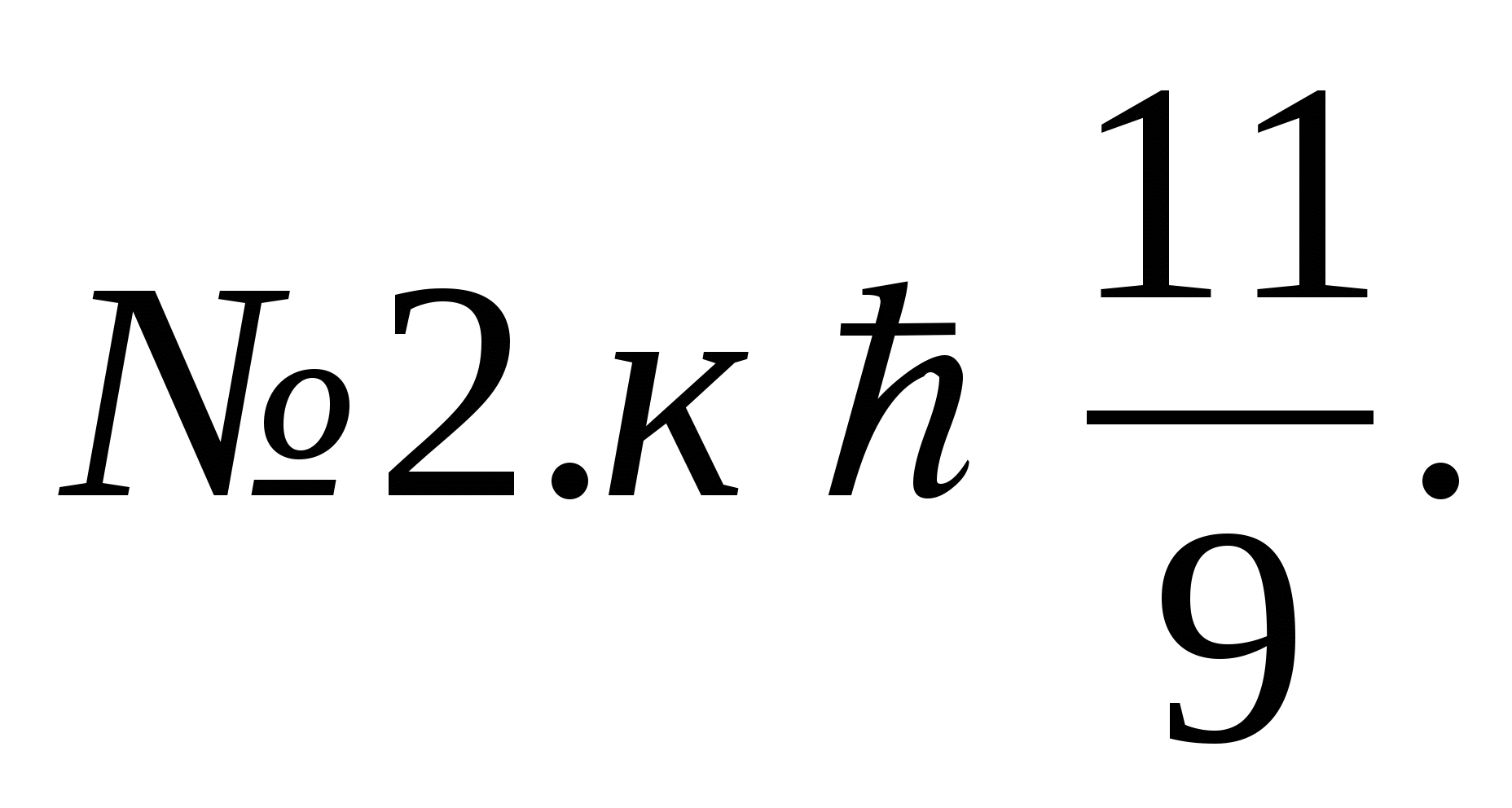
![]()
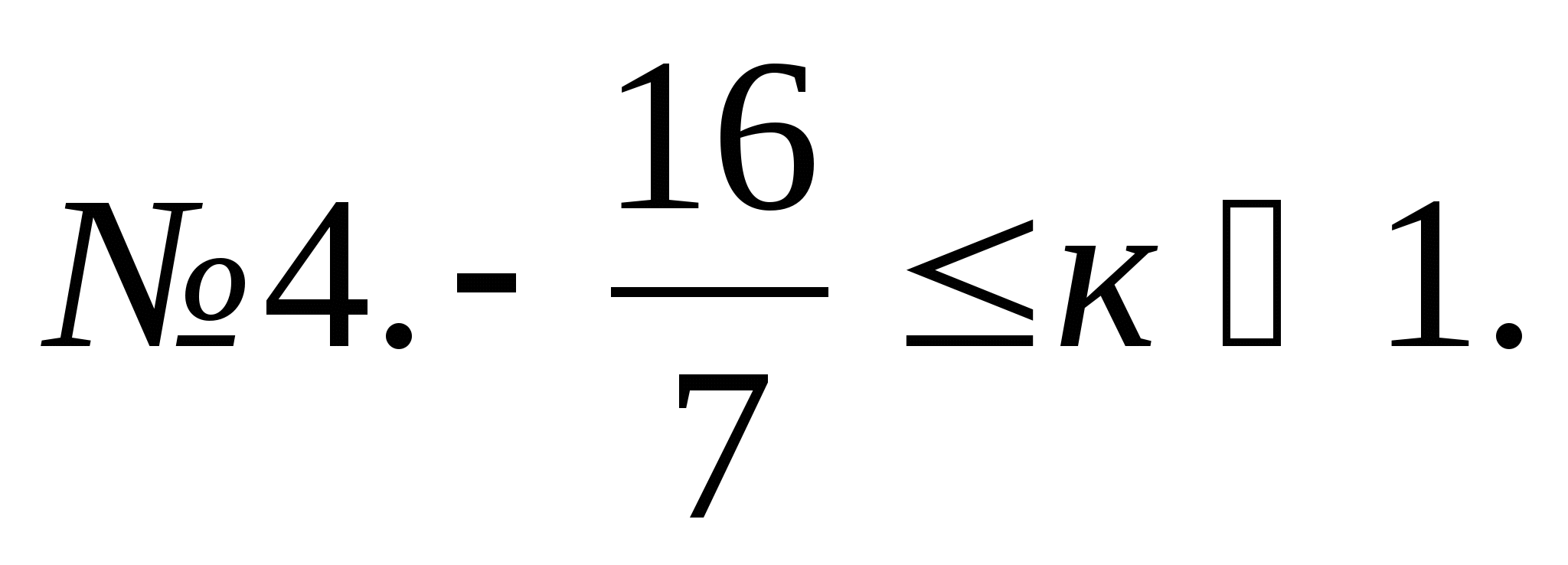
![]()
![]()
![]()
![]()
![]()
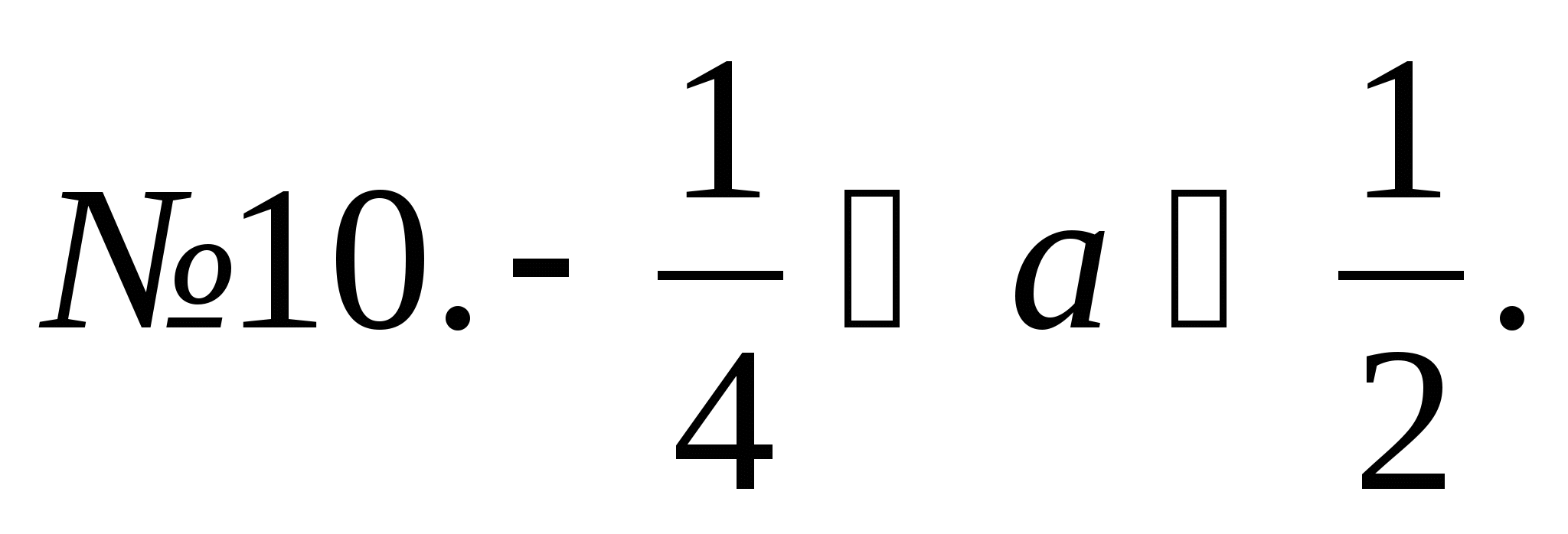
![]() и
и
![]()
Задания на определение количества корней квадратного трёхчлена
-
При каких значениях
 уравнение
уравнение
![]()
имеет единственное решение?
-
При каких значениях
 уравнение
уравнение
![]()
имеет единственное решение?
-
При каких значениях
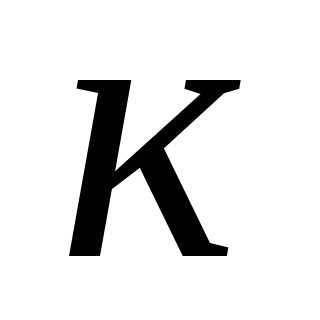 уравнение
уравнение
![]()
имеет более одного корня?
-
При каких значениях
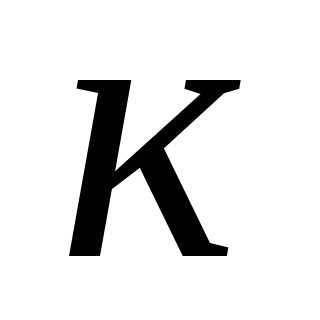 уравнение
уравнение
![]()
имеет корни? Приведите пример положительного
значения ![]()
-
При каких значениях
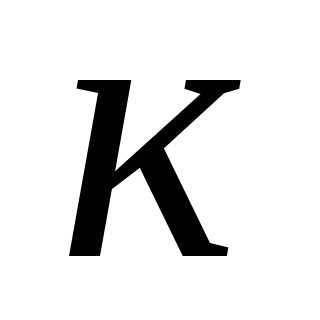 уравнение
уравнение
![]()
не имеет корней? Приведите пример отрицательного
значения ![]()
-
Найдите все целые значения
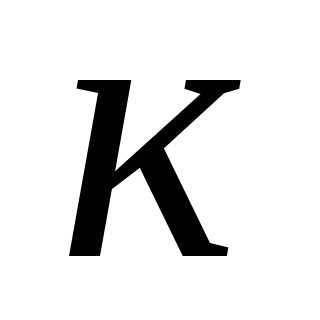 , при которых уравнение
, при которых уравнение
![]()
имеет два корня?
-
Найдите все целые значения
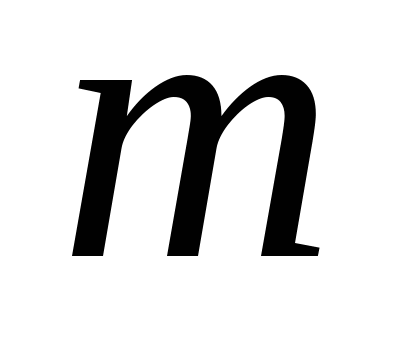 , при которых уравнение
, при которых уравнение
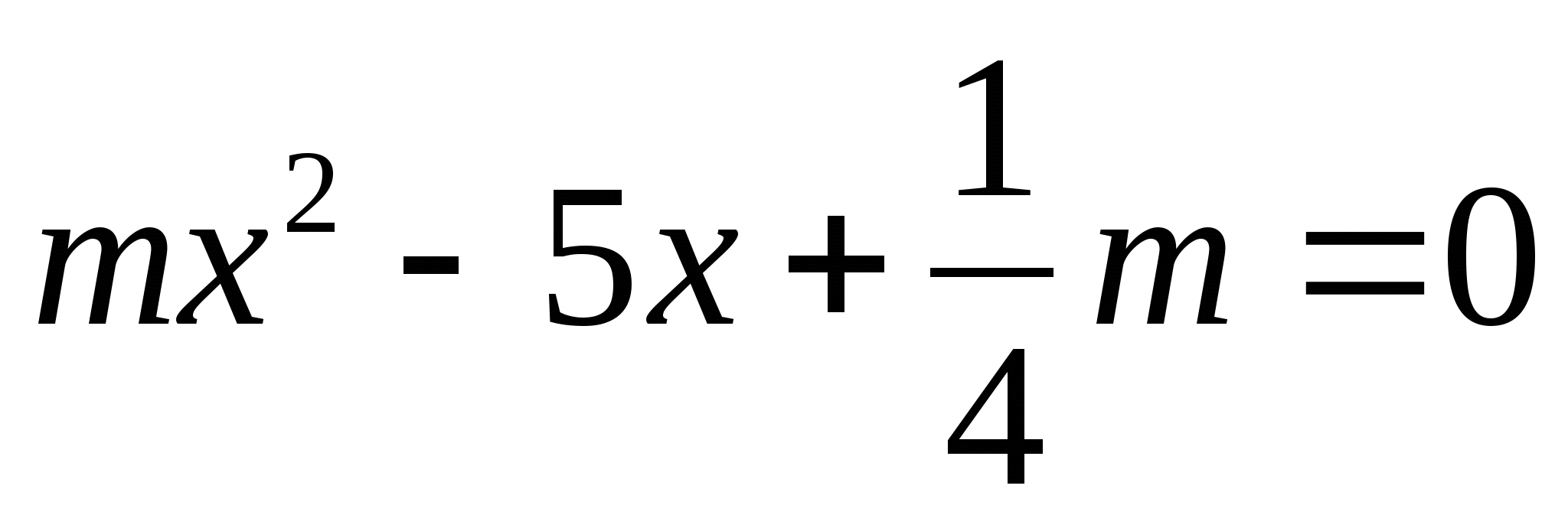
имеет два корня?
-
При каком значении
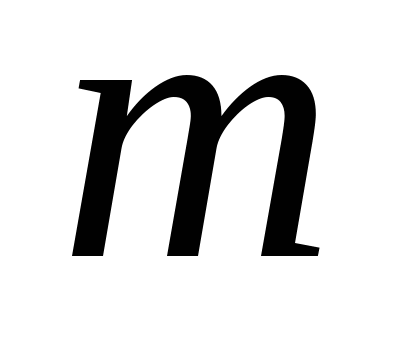 уравнение
уравнение
![]()
имеет два корня? Найдите эти корни.
-
При каком значении
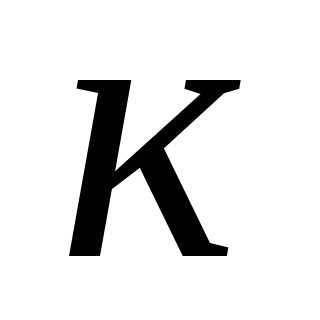 уравнение
уравнение
![]()
имеет два корня? Найдите эти корни.
-
При каких значениях
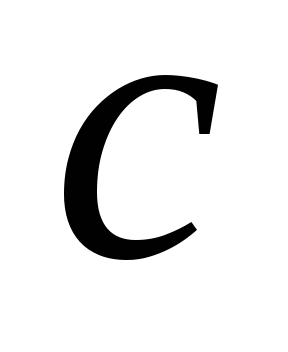 уравнение
уравнение
![]()
имеет корни?
-
При каких значениях
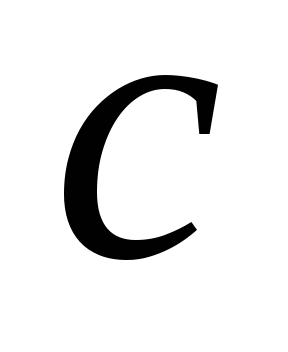 уравнение
уравнение
![]()
имеет корни?
-
При каких значениях параметра
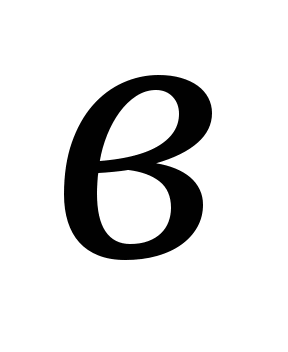 корни уравнения
корни уравнения
![]()
равны по модулю?
-
Найдите наибольшее целое значение
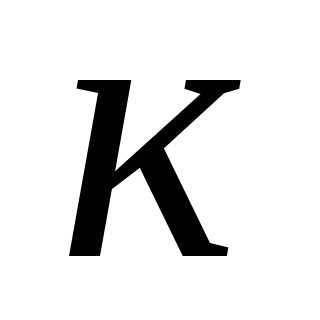 , при котором уравнение
, при котором уравнение
![]()
не имеет действительных корней.
-
Найдите наименьшее целое значение
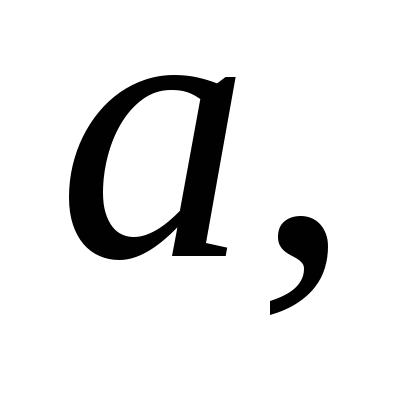 при котором уравнение
при котором уравнение
![]()
имеет два различных корня.
-
При каком значении
 уравнение
уравнение
![]()
имеет один корень?
-
При каком значении
 уравнение
уравнение
![]()
имеет один корень?
-
При каких значениях
 уравнение
уравнение
![]()
имеет более двух корней?
Ответы
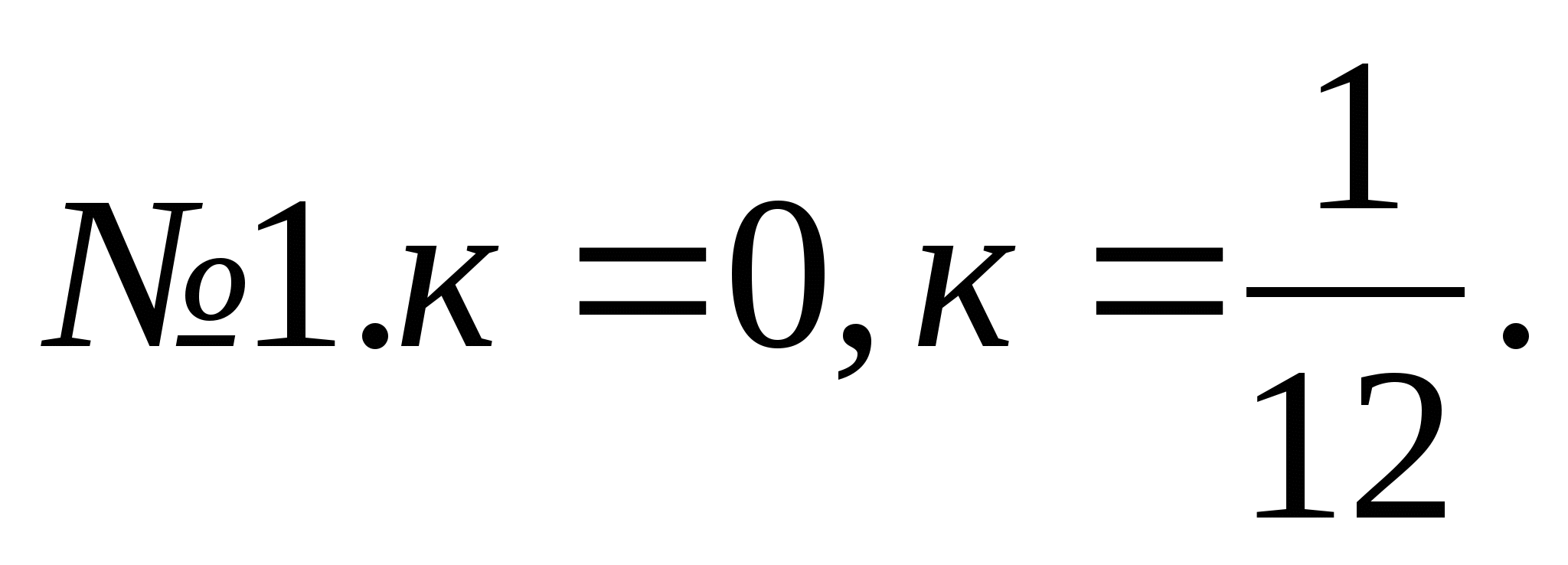
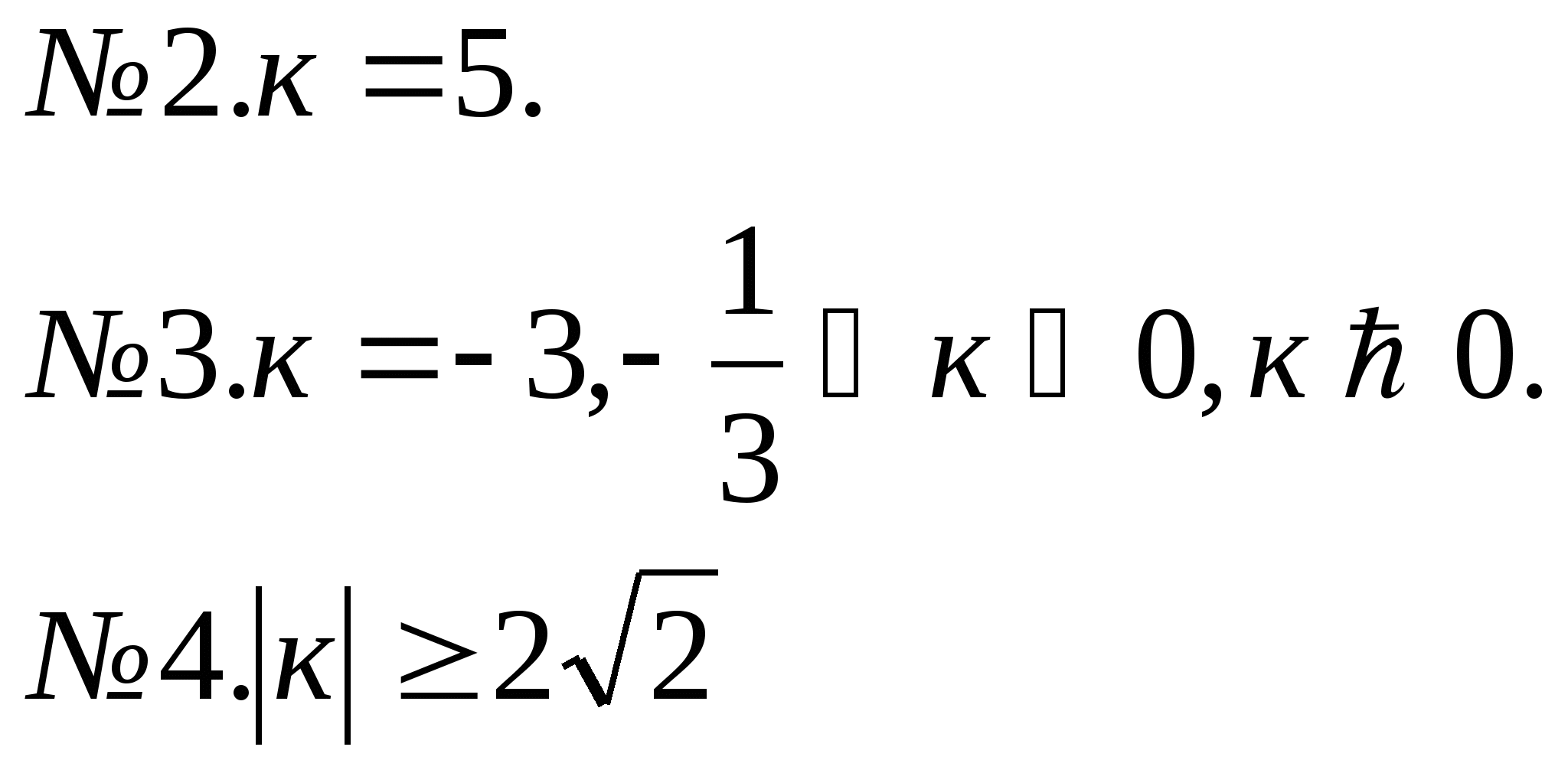
![]() .
.
