Разработка урока на тему Функция (9 класс)

У Р О К - С И М П О З И У М

по теме «ФУНКЦИЯ» (А-9)

Учитель:

Красноруцкая

Людмила

Александровна

Э П И Г Р А Ф

к уроку:

«Многие науки устанавливают связи между объектами.

Но только математика рассматривает абстрактные переменные величины и связи между ними»

Цели урока:

а) образовательная: развить умения и навыки учащихся в работе с формулой и графиками по данной теме;

б) воспитательная: показать большое значение данной темы в курсе математики, учить трудиться, самостоятельно думать, приучать к аккуратности, внимательности;

в) развивающая: заставить каждого ученика поверить в свои знания, в свои силы, помочь подняться ему на новую ступеньку открытий, продолжать развивать познавательный интерес к предмету.

План урока-симпозиума:

1. Вступительное слово учителя.

2. Функция в математике и других науках.

3. 2 способа задания функции.

4. Основные задачи.

5. Готовимся к тестированию.

6. Из истории.

Оборудование:

1. Методическая литература.

2. Историческая литература.

3. 3 плаката.

4. 14 карточек.

5. Рефераты учащихся.

Учитель:

Уважаемые гости!

Сегодня вы присутствуете на симпозиуме. Тема его - «Функция». Цель его: расширить знания слушателей по данной теме, убедить всех присутствующих в важности этой темы, в особом месте данной темы в курсе математики. Слово «симпозиум» в переводе с греческого означает «пир». Впервые симпозиум организовали Платон и Сократ. Задача любого симпозиума - разрешение той или иной проблемы. А сегодня у нас с вами одна проблема - функция и какие с ней можно решать интересные задачи. На симпозиуме работают 3 секции: теоретическая, практическая, историческая. Да помогут вам бог времени - Крон и богиня мудрости - Афина.

К доске - 4 ученика (работа с плакатом № 1).

1. Математика держится на четырёх «китах». Один из «китов» - функция. Существует много задач в геометрии, физике, экономике, которые можно объединить на языке чисел, формул, схем. Посмотрите на формулы из физики:

F = -k·x (закон Гука)

S(t) = gt² /2 + V_о · t + S (максимальная высота взлёта)

Вопрос классу: какие вы видите функции? Дайте им определение

(у = кх +в; у = ах² + вх + с)

2. Функция играет большую роль в познании мира. Возьмём экономику. Немецкий учёный Энгель открыл функцию спроса: по оси Х - уровень дохода семей, по оси Y - величина спроса на товар. Видим: функция возрастающая - растёт доход, растёт и спрос.

3. Рассмотрим функцию y = х². На первый взгляд простовата, а на самом деле:

а) геодезист видит в ней площадь квадрата;

б) авиаконструктор - зависимость высоты подъёма от скорости.

4. Именно математике принадлежит ведущая роль в формировании мышления, в развитии умений действовать по заданной схеме. Существует 4 способа задания функции. Так как время ограничено, предлагаю уделить внимание графическому и аналитическому способам.

Учитель: «Ну что же! Прислушаемся к совету одноклассника. С какого способа начнём?

Ученик: «С графического».

Практикум № 1.

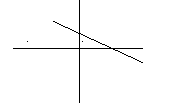
I. Центральная доска (на доске заготовлены 4 рисунка).

1.

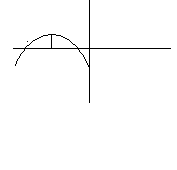
2.

3.

4.

1) определить знаки коэффициентов;

2) написать уравнение прямой;

3) решить неравенство: х³ - 4х >=0;

4) найти Д (у) и Е (у).

2. 2 человека на месте (творческая группа).

Арка моста имеет высоту 4 м, наибольшую ширину - 20 м. Составить уравнение параболы.

3. Класс работает устно (повторяется теория функции и решаются задачи).

а) у = - х²+ 5; б) у = х/2; у = 2/х

у = 2 ( х - 4)²; у = 2х

Расскажи о параболе у = 2х - 1. Нарисуй схематично.

в) у = /х/; у = - 6/х; у = (х)^1/2.

Найти: Д (у) и Е (у).

Итог: выслушать ответы 4-х учащихся, а также творческой группы.

Практикум № 2. Построение графиков функции.

1. У центральной доски 4 человека.

а) у = /х - 1/ + /х + 2/ - построить методом линейного сплайна.

х

- 3

- 2

1

2

у

5

3

3

5

б) сравнить графики 2-х функций: у = х² - 2х и у = (х³- 2х² )/х

в) построить: у = 6/(/х/ + 1) - 3

г) построить: /у/ = /х/ + 1.

2. У боковой доски творческая группа:

у = {1/5х² - 6; - 5 <= х <= 5

{1/2 (х - 1)² - 5; - 1,5 <= х <= 3,5

{- (х + 3)² + 3; - 5 <= х <= -1

(цыплёнок дорисовывается)

3. Класс: у = /х² - 4/х// - построить и описать свойства

а) все работы проверяются;

ИТОГ: б) выходит к доске ученик: «Графический способ задания функции - один из самых удобных и наглядных способов информации». Метеорологическая служба, геологи, врачи и другие пользуются графиками. Поэтому мы должны уметь работать с графиком, т.е. описывать свойства функций и строить графики, используя знание теории построения графиков функции, а также их преобразования.

Учитель: «Коротко подведём итоги: какие функции повторили, какие свойства, какие преобразования?» (класс отвечает)

Практикум № 3.

Ученик с места: «Мне, кажется, мы увлеклись графическим способом. Мне больше нравится работать с функцией, заданной аналитическим способом, т.е формулой.

Учитель: полностью согласна. Нас ждут интересные задачи с формулами функций.

1. К доске идут 5 человек:

а) найти точку пересечения прямых

{3х + 4у = 9

{6х + 5у = 0

б) решить неравенство: х² (3 - х) / (х² - 9) >=0;

в) решить уравнение: х³ - 2/х + (х)^1/2 = 0;

г) у = (2а - 3)х + 5. При каких значениях «а» функция возрастает?

д) найти область определения функции:

у = (4х² + 11х - 3)^1/6 / (1 - 6/(х + 11))

(задания на карточках)

Творческая группа (4 группы по 2 человека, остальные тест).

1. у = 12 / (х² + 2х +7)

Найти наибольшее значение функции. Сообрази!

2. Решить уравнение: х³ - 2/х + (х)^1/2 = 0 - примени свойство монотонности.

Класс пишет тест (см. «Работа с формулой. Тест»)

Работы сдаются, проверяются учителем.

Практикум № 4. Применений функции.

К доске выходит ученик с плакатом. «Мне, кажется, на данном этапе изучения функции самой интересной является квадратичная функция. Рассмотрим её применение: перед нами канал. Привезли 6000 м² для облицовки дна и стен. При каких размерах канала, учитывая, что длина 1 км, объём воды наибольший?

Пусть Х м - ширина канала

V = х h 1000 (1 км = 1000 м)

S = 1000 х + 2 h * 1000

1000 (х + 2h) = 6000

х = 6 - 2h

h = 3 - 0,5х

V = 1000 х (3 - 0,5х) = - 500х² + 3000х. Это квадратичная функция.

m = - в/2а = - 3000/- 1000 = 3, х = 3, h = 1,5.

Я показал применение квадратичной функции.

Учитель: «А теперь немного истории. И можно заканчивать работу симпозиума, готовиться к обмену своих мнений по поводу успешной или неуспешной работы симпозиума».

Ученик: понятие функции уходит в ту далёкую эпоху, когда люди поняли, что окружающие явления взаимосвязаны. В Древнем Вавилоне составляли таблицы квадратов и кубов. Птолемей составлял тригонометрические таблицы. В 14 веке французский математик Николай Оресл описывал явления природы с помощью графиков функций. Французский математик Рене Декарт ввёл переменные величины и систему координат. В 17 веке Готфрид Лейбниц вводит термин «функция». Леонард Эйлер (18 в.) вводит определение функции и только в 19 в. Лобачевский окончательно создаёт теорию функции. В начале 20 в. на базе теории функций возникла новая ветвь математики - функциональный анализ. Это очень абстрактная наука, но благодаря ей развиваются физика, экономика.

Учитель: Ну вот и всё, «встреча» с функцией подошла к концу. Ваши впечатления - что понравилось на уроке, что узнали нового, чему научились, что хочется ещё узнать о функции, чьи ответы и выступления запомнились? (учащиеся высказывают своё мнение). Благодарю организаторов и участников симпозиума. Желаю вам творческих успехов в дальнейшем изучении этой темы в школе и в вузе. Эволюция функции продолжается. Ждём новых открытий от вас, мои дорогие!