- Учителю
- Задачи для проведения зачёта в 10 классе по теме 'Многогранники'
Задачи для проведения зачёта в 10 классе по теме 'Многогранники'
Предлагаю набор задач по стереометрии, которые я использую для проведения зачёта в 10 классе после изучения темы «Многогранники».
Условия задач ученикам известны заранее, на подготовку даётся несколько дней с возможностью проконсультироваться с учителем при возникающих затруднениях. Для подготовки к зачёту необходимо повторить понятия:
Угол между скрещивающимися прямыми;
Расстояние между скрещивающимися прямыми;
Угол между прямой и плоскостью;
Линейный угол двугранного угла;
Признаки:
Параллельности прямой и плоскости;
Перпендикулярности прямой и плоскости;
Перпендикулярности плоскостей;
Теорему о трёх перпендикулярах.
В задачах слово найти следует понимать: показать и обосновать. В случаях, если искомый угол равен 90° достаточно доказать соответствующую перпендикулярность.
1. В кубе АВСDА1В1С1D1 найти :
Угол между ребром АА1 и диагональю В1D;
Угол между прямой АС1 и плоскостью грани DD1С;
Расстояние между прямыми АС и А1В1.
Угол между плоскостями АВ1С и А1В1С.
2. В кубе АВСDА1В1С1D1 найти:
Угол между прямыми В1С и ВD;
Расстояние между прямыми ВА1 и В1С1;
Угол между прямой А1В и плоскостью АВС;
Угол между плоскостями ВА1С1 и ВА1D1.
3. В прямоугольном параллелепипеде АВСDА1В1С1D1 боковое ребро равно диагонали основания. Найти:
Угол между ВD и А1С1;
Угол между прямой АС1 и плоскостью BВ1С;
Угол между плоскостью основания и плоскостью АА1С.
Сечение плоскостью, проходящей через середину ребра АD перпендикулярно ВD1;
4. В прямоугольном параллелепипеде АВСDА1В1С1D1 найти:
Угол между прямыми АВ и ОС1, где О - точка пересечения диагоналей основания;
Угол между прямой АВ1 и плоскостью АВС1, если ВВ1=ВС;
Угол между плоскостями АВС1 и АА1D;
Сечение, проходящее через точки О, С, параллельно прямой А1В.
5. В правильной призме АВСА1В1С1 найти:
Угол между прямыми АС1 и D1С;
Угол между прямой А1В и плоскостью АА1С;
Угол между плоскостями ВСА1 и ВВ1С1;
Расстояние между прямыми СС1 и А1В.
6. В основании прямой призмы АВСА1В1С1- равнобедренный прямоугольный треугольник с прямым углом В. Найти:
Угол между прямыми ВС1 и АС;
Угол между прямой ВС1 и плоскостью АА1С;
Угол между плоскостями АВ1С и АСВ;
Сечение, проходящее через центр описанной окружности основания, перпендикулярно ребру АВ.
7. В основании прямой призмы АВСDА1В1С1D1 - ромб, АВ=ВД. О - точка пересечения диагоналей нижнего основания. Найти:
Угол между прямыми АС и ВD1;
Угол между прямой АС1 и плоскостью ВВ1D;
Расстояние между прямыми А1А и В1D1;
Угол между плоскостями АВС и А1В1С.
8. В правильной четырёхугольной пирамиде РАВСD О-точка пересечения диагоналей основания. Найти:
Угол между прямыми РО и АВ;
Угол между прямой РС и плоскостью ВРD;
Угол между плоскостями АРD и ВРС;
Сечение, проходящее через точки В, О, параллельно прямой АР.
9. В правильной треугольной пирамиде РАВС найти :
Угол между прямыми МК и РС, где М -середина ребра АВ, К - середина высоты пирамиды;
Угол между прямой АР и плоскостью ВРС, если АО=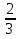 АР;
АР;
Угол между плоскостью АВС и плоскостью MВК;
Сечение плоскостью, проходящей через точку К, перпендикулярно АВ.
10. В пирамиде DАВС ребро DА перпендикулярно плоскости основания, АВ = ВС=АС. Найти:
Угол между прямыми DО и ВС, где О - центр основания;
Угол между прямой АВ и плоскостью АСD;
Угол между плоскостями АВD и ОАD;
Сечение плоскостью, проходящей через точку О параллельно грани АВD.
11. В пирамиде РАВСD в основании квадрат, О- середина ребра АВ, РО перпендикулярно плоскости основания. Найти:
Угол между прямыми АР и ВС;
Угол между прямой РС и плоскостью АВС;
Угол между плоскостями АРВ и РВС, если АР=АD;
Сечение плоскостью, проходящей через центр квадрата, перпендикулярно грани РDС.
12. В правильном тетраэдре РАВС найти:
Угол между прямыми АP и ВС;
Угол между прямой ВС и плоскостью АPС;
Сечение плоскостью, проходящей через середины рёбер АВ, АС и PС;
Угол между полученной плоскостью и плоскостью АВС.