- Учителю
- Обобщающий урок по теме «Решение логарифмических уравнений» Алгебра и начала анализа. 11 класс
Обобщающий урок по теме «Решение логарифмических уравнений» Алгебра и начала анализа. 11 класс
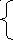



 Обобщающий урок по теме «Решение логарифмических уравнений»
Обобщающий урок по теме «Решение логарифмических уравнений»
(учитель Клокова Т.Ю. МБОУ СКОШ №36 г. Озерск Челябинской области)
Цель: 1. Обобщить и систематизировать знания учащихся по данной теме.
2. Расширить знания учащихся.
3. Учить находить «красивое» решение уравнений.
4. Показать нестандартные подходы к решению комбинированных уравнений.
План:
-
Фронтальный опрос
-
Методы решения логарифмических уравнений.
-
«Учимся на чужих ошибках»
-
Решение комбинированных уравнений.
-
Обучающая самостоятельная работа.
-
Задание на дом (дать комментарии к решению)
-
Итог урока.
Фронтальный опрос
Дать определение уравнения
Равенство, содержащее переменную, называется уравнением.
Что значит решить уравнение?
Решить уравнение - значить найти его корни или доказать, что корней нет.
Что такое корень уравнения?
Значение переменной, при которой уравнение обращается в верное равенство, называется корнем уравнения.
Что такое область определения уравнения?
Областью определения уравнения называется множество значений переменной уравнения f(x)=g(x), при которых одновременно имеют смысл f(x) и g(x).
Какие уравнения называются равносильными?
Уравнения, имеющие одинаковые корни или не имеющие корней называются равносильными.
Следствия равносильности
-
Если к обеим частям уравнения f(x)=g(x) прибавить одну и ту же функцию у(х) определенную при всех значениях переменной из области определения данного уравнения, то уравнение f(x)+ у(х) =g(x)+у(х) равносильно данному.
-
Если к оби части уравнения f(x)=g(x) умножить или разделить на одно и то же число, отличное от нуля, то получится уравнение равносильное данному.
Равносильны ли уравнения?
-
 (да)
(да)
-
 (нет)
(нет)
(нет)
 (нет)
(нет)
Что такое логарифм?
Логарифмом положительного числа b по основанию a (а>0, a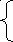 ) называется показатель степени Х, в которую нужно возвести а, чтобы получить b, т. е
) называется показатель степени Х, в которую нужно возвести а, чтобы получить b, т. е
Какое уравнение называется логарифмическим?
Уравнение, в котором переменная находится под знаком логарифмической функции.
Свойства логарифмов
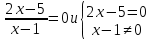

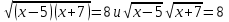 -
-

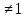

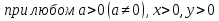

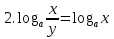
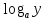
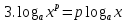
При решении логарифмических уравнений применяются следующие методы:
-
Решение уравнений, основанное на применении определения логарифма.
-
Решение с помощью потенцирования.
-
Применение основного логарифмического тождества.
-
Введение новой переменной.
-
Использование логарифмирования.
-
Переход к логарифму с новым основанием.
( При решении логарифмических уравнений необходима проверка все найденных корней или нахождения области определения уравнения, т.е. соблюдение равносильных переходов)
-
Метод, основанный на определении логарифма
 .
.
По определению логарифма имеем:
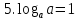 , то есть
, то есть  (свели уравнение к показательному уравнению, которое решается методом введения нового неизвестного),
(свели уравнение к показательному уравнению, которое решается методом введения нового неизвестного),
 .
.
Следовательно 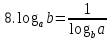 .
.
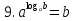 : 2 корня, по обратной теореме Виета имеем:
: 2 корня, по обратной теореме Виета имеем: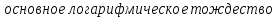 ,следовательно
,следовательно
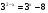 - не удовлетворяет условию
- не удовлетворяет условию 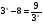 .
.
Имеем: 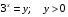 .
.
Проверка: если  , тогда
, тогда
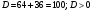

 - верно.
- верно.
Ответ:  .
.
-
Метод, использующий монотонность логарифмической функции (метод потенцирования).
Для каждой монотонной функции 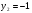 из равенства
из равенства  следует, что
следует, что  .
.
Рассмотрим уравнение вида  при
при 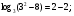 решением этого уравнения будут все те решения уравнения
решением этого уравнения будут все те решения уравнения 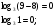 , для которых
, для которых 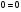 (или
(или 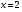 ).
).
Поэтому уравнение 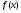 можно решить по алгоритму:
можно решить по алгоритму:
-
Найти ОДЗ уравнения;
-
Решить на ОДЗ этого уравнения равносильное ему уравнение
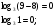 .
.
Конечно, не все уравнения будут иметь вид 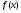 , поэтому необходимы будут преобразования, используя свойства логарифмической функции.
, поэтому необходимы будут преобразования, используя свойства логарифмической функции.
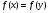
Так как 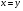 , то
, то 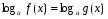 ;
; 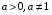 , получаем
, получаем 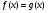 .
.
Исходное уравнение, используя свойства логарифмической функции можно представить в виде:
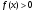 данное уравнение при
данное уравнение при 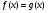 равносильно уравнению:
равносильно уравнению:
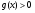 .
.
Возведем в квадрат, получим
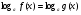

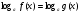
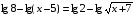 следовательно, уравнение имеет два корня:
следовательно, уравнение имеет два корня:
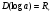 , так как
, так как 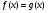 , то
, то 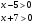 посторонний корень.
посторонний корень.
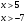 .
.
Ответ:  .
.
Замечание: переход от равенства  к равенству
к равенству  называется потенцированием по основанию
называется потенцированием по основанию 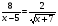 при
при 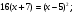 . Совершая потенцирование мы совершаем переход, не являющийся равносильным, поэтому нужна проверка.
. Совершая потенцирование мы совершаем переход, не являющийся равносильным, поэтому нужна проверка.
-
Применение основного логарифмического тождества

Найдем ОДЗ:
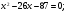 ;
;  ;
;  , следовательно
, следовательно  .
.
Применив в правой части основное логарифмическое тождество, получим:
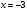 , следовательно, уравнение примет вид:
, следовательно, уравнение примет вид:
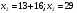 .
.
Используя определение логарифма, получаем:
 ;
;
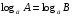 .
.
Пусть 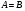 , имеем:
, имеем: 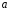
 ;
;
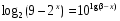 ;
;
 следовательно, 2 корня
следовательно, 2 корня
 ;
; 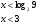 .
.
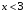 или
или 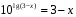 .
.
Но 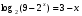 не входит в ОДЗ, следовательно, это посторонний корень.
не входит в ОДЗ, следовательно, это посторонний корень.
Ответ: 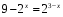 .
.
-
Применение логарифмирования.
Логарифмирование по основанию 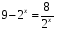 представляет собой переход от равенства
представляет собой переход от равенства  к равенству
к равенству 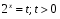 , для этого
, для этого 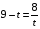 .
.
Решим уравнение 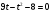 .
.
Уравнение содержит неизвестную величину, как в основании, так и в показателе степени, его можно решить, логарифмируя левую и правую часть по основанию 10, так как в условии уже имеется десятичный логарифм. Получаем:
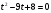 , где
, где 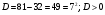 .
.
 .
.
Введем новую переменную  и учитывая, что
и учитывая, что 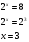 получаем:
получаем:
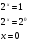
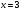 или
или  .
.
Вернемся к замене:
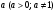 или
или 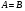
Оба корня удовлетворяют ОДЗ. Все преобразования были тождественны, следовательно, оба корня являются решение уравнения.
Ответ:  .
.
-
Введение нового неизвестного
 ОДЗ
ОДЗ  .
.

Пусть  , тогда
, тогда
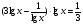 .
.
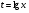 по обратной теореме Виета получаем:
по обратной теореме Виета получаем:
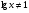 ;
; 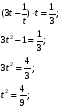 .
.
 или
или  .
.
Оба корня входят в ОДЗ.
Ответ: 10; 10000.
-
Переход к логарифму по новому основанию
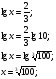
Найдем ОДЗ:
 ;
;  , следовательно,
, следовательно, 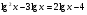 .
.
Перейдем в уравнении к логарифму по основанию 3, получим:
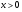 , следовательно,
, следовательно,
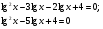 .
.
Введем новое неизвестное 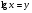 , получаем:
, получаем:
 , что тождественно
, что тождественно 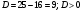
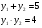 , следовательно, 2 корня.
, следовательно, 2 корня.

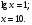 ;
; 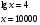 .
.
Получаем:
 или
или 
Оба корня больше -1 и не равны нулю, то есть входят в ОДЗ.
Ответ:  ; 8.
; 8.
Учимся на чужих ошибках.
-
Решить уравнение

Решение: логарифмируем обе части уравнения по основанию 3.


Ответ:  .
.
Приведенное решение не верно. Логарифмировать данное уравнение нельзя, так как выражение 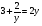 . Функция в левой части уравнения принимает только положительные решения, поэтому исходное уравнение решений не имеет.
. Функция в левой части уравнения принимает только положительные решения, поэтому исходное уравнение решений не имеет.
Ответ: решений нет.
-
Решить уравнение
 .
.
Используя свойства логарифмов, имеем:
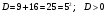
Ответ: 0; 4.
Приведенное решение не верно, так как нет проверки или оценки ОДЗ. 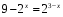 является посторонним корнем.
является посторонним корнем.
Ответ: 4.
-
Решить уравнение
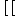
 , что тождественно
, что тождественно  ;
;

Ответ: 5.
Решение не верно, так как нет проверки и нарушена операция потенцирования. Верный ответ 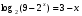 .
.
-
Решить уравнение
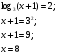
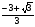
 ;
; 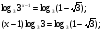 ;
;
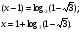 ;
;
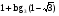 .
.
Ответ: 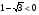 .
.
Решение не верно, так как не учтено условие 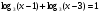 , исходя из которого
, исходя из которого 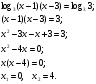 , следовательно корень
, следовательно корень 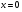 не входит в ОДЗ.
не входит в ОДЗ.
Ответ: 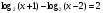 .
.
Решение комбинированных уравнений (задания повышенной сложности)
Чем осложнено это уравнение? Какие нужны знания при решении этого уравнения?
Решение:
Найдем ОДЗ:
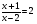 ;
;  ;
; 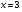 .
.
 ;
;
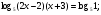
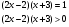 ;
;
 .
.
По определению модуля имеем:
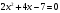
Рассмотрим два случая:
Первый случай: 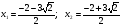 ;
; 
Решим неравенство 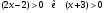 методом параболы. Получим
методом параболы. Получим  .
.
 отсюда получаем
отсюда получаем  .
.
Второй случай:  ;
;  , следовательно,
, следовательно, 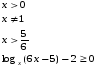 .
.
Ответ:  ;
; 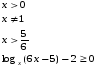
Найдем ОДЗ:  , следовательно, корни лежат в I четверти:
, следовательно, корни лежат в I четверти: 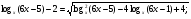 .
.
Перейдем к основанию 10:
 , следовательно,
, следовательно,
 ;
;
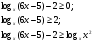

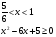 , делим на
, делим на 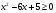 , так как из ОДЗ
, так как из ОДЗ 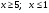 .
.
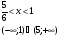

 .
.
Выберем корни, лежащие в I четверти, получаем 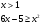 .
.
Ответ: 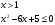 .
.
Самостоятельная работа
Вариант 1
Решить уравнение  .
.
Найдем ОДЗ: 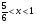 ;
; 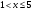 , следовательно
, следовательно 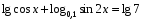 .
.
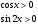
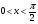 возведем в квадрат, оно равносильно при
возведем в квадрат, оно равносильно при 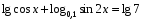 .
.

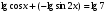 , следовательно, 2 корня.
, следовательно, 2 корня.
 - не удовлетворяет ОДЗ
- не удовлетворяет ОДЗ
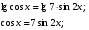 .
.
Ответ: 13.
Вариант 2
Решить уравнение 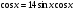 .
.
 ;
;
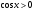
 или
или  .
.
Проверка: при  получаем:
получаем: 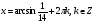 - верно.
- верно.
При  получаем
получаем 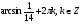 , не удовлетворяет, так как основание логарифма должно быть положительным.
, не удовлетворяет, так как основание логарифма должно быть положительным.
Ответ: 0.
*** МФТИ
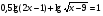
ОДЗ: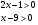
Используем свойства логарифмов
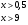
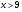

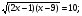 *
*
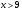
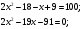 подставим в *
подставим в * 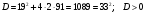 +0,22=0, сл.
+0,22=0, сл.
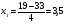

D=1+2,24=3,24=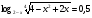
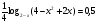 или
или
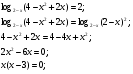
Решим уравнение: 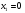
Используя формулы 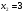 получим:
получим:
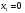 , пусть
, пусть 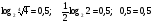 , то
, то 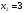

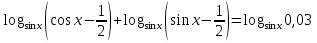
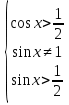
6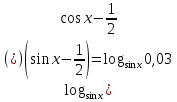
D=25-24=1
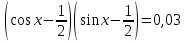
1)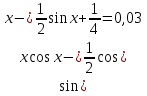 ,
,
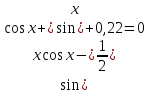
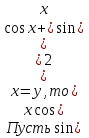
 ,
,

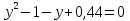
Ответ:
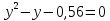 ,
,

Итог урока.
Домашнее задание (дать комментарий):

2.  )
)
3.