- Учителю
- Сборник олимпиадных задач по математике для 5 класса (с ответами и решениями)
Сборник олимпиадных задач по математике для 5 класса (с ответами и решениями)





Сборник олимпиадных задач по математике
для 5 класса
( с ответами и решениями)
Составитель: учитель математики высшей категории
Максимова Н.М. ГБОУ ШКОЛА № 2036 г Москва
Содержание:
1. Разные задачи............................................................
2.Метод графов..............................................................
3.Табличный способ.......................................................
4.Задачи на переливание...............................................
5.Задачи на взвешивание..............................................
6.Задания на восстановление записей
вычисления.................................................................
7. Олимпиадные задачи ( дистанционные олимпиады,
конкурс "Кенгуру", "Математическая карусель")......
ГЛАВА 1: Разные задачи
Задача 1:
В пещере старый пират разложил свои сокровища в 3 цветных сундука, стоящих вдоль стены: в один - драгоценные камни, а в другой - золотые монеты, а в третий - оружие. Он помнит, что :
- красный сундук правее, чем драгоценные камни
- оружие правее, чем красный сундук.
В сундуке какого цвета лежит оружие, если зелёный сундук стоит левее, чем синий?
Решение :
ДК - зелёный
ЗC - красный
О - синий
Задача 2 :
Девять осликов за 3 дня съедают 27 мешков корма.
Сколько корма надо пяти осликам на 5 дней?
Решение :
1 шаг 9 осликов в 1 день - 27 : 3= 9м.
2 шаг 1 ослик в 1 день - 9 : 9 = 1 м.
3 шаг 5 осликов в 1 день - 5 * 1 = 5 м.
4 шаг 5 осликов за 5 дней - 5 * 5 = 25 м.
Задача 3 :
Кенгуру мама прыгает за 1 секунду на 3 метра, а её маленький сынишка прыгает на 1 метр за 0,5 секунды.
Они одновременно стартовали от бассейна к эвкалипту по прямой.
Сколько секунд мама будет ждать сына под деревом, если расстояние от бассейна до дерева 240 метров
Решение :
1 шаг 240 : 3 = 80 (с) скакала мама Кенгуру
2 шаг сын за 0,5 с - 1 м, за 1 с - 2 м
3 шаг 80 * 2 = 160 (м) проскачет кенгурёнок за 80 с
4 шаг 240 - 160 = 80 (м) осталось проскакать кенгурёнку когда
мама уже под эвкалиптом
5 шаг 80 : 2 = 40 (с)
Ответ: 40 секунд.
Задача 4 :
На скотном дворе гуляли гуси и поросята.
Мальчик сосчитал количество голов, их оказалось 30, а затем он сосчитал количество ног, их оказалось 84.
сколько гусей и сколько поросят было на школьном дворе?
Решение :
1 шаг Представьте, что все поросята подняли по две ноги вверх
2 шаг на земле осталось стоять 30 * 2 = 60 ног
3 шаг подняли вверх 84 - 60 = 24 ноги
4 шаг подняли 24 : 2 = 12 поросят
5 шаг 30 - 12 = 18 гусей
Ответ: 12 поросят и 18 гусей.
Задача 5
Инженер ежедневно приезжал на станцию в одно и то же время, и в то же время за ним подъезжала машина, на которой он ехал на завод.
Однажды инженер приехал на станцию на 55 мин раньше обычного.
Сразу пошел навстречу машине и приехал на завод на 10 мин раньше, чем обычно.
Во сколько раз скорость инженера меньше скорости машины?
Решение:
За 10 мин машина проходит путь, равный двойному расстоянию от станции до места встречи инженера с машиной.
Значит, путь от станции до места встречи машина проходит за 5 мин.
На месте встречи машина была за 5 мин до времени обычного приезда инженера на станцию, значит, путь от станции до места встречи инженер шел 55 мин - 5 мин = 50 мин.
Следовательно, скорость инженера в 50 : 5 = 10 раз меньше скорости машины.
Задача 6
В триседьмом царстве живут драконы.
У каждого дракона одна, две или три головы,
а) Может ли у 40 % драконов быть 60 % голов?
б) Может ли у 40 % драконов быть 70 % голов?
Решение:
а) Покажем, что у 40% драконов может быть 60% голов.
Пусть в этом царстве живет 100 драконов: 40 драконов с одной головой, 20 - с двумя головами и 40 - с тремя.
Тогда число голов у всех драконов равно
40 • 1 + 20 • 2 + 40 • 3 = 200.
При этом все 40 трехглавых драконов, что составляет 40% от общего числа драконов, имеют 40 • 3 = 120 голов, что составляет
120/200 • 100% = 60% от общего числа голов.
б) Пусть число драконов равно х, а общее число голов у них равно у.
Предположим, что какие-то 40% драконов имеют 70% голов.
Тогда, поскольку каждый из этих драконов имеет не более трех голов, то 0,7у = 3 • 0,4х.
С другой стороны, поскольку остальные 60% драконов имеют 30% голов и у каждого из них не менее одной головы, то 0,6х = 0,3y.
Но эти неравенства не могут выполняться одновременно, так как они равносильны соответственно 7у = 12х и 12x = 6у.
Поэтому у 40% драконов не может быть 70% голов.
Задача 7
В пещере старый пират разложил свои сокровища в 3 цветных сундука, стоящих вдоль стены: в один - драгоценные камни, а в другой - золотые монеты, а в третий - оружие. Он помнит, что :
- красный сундук правее, чем драгоценные камни
- оружие правее, чем красный сундук.
В сундуке какого цвета лежит оружие, если зелёный сундук стоит левее, чем синий?
Решение :
ДК - зелёный
ЗC - красный
О - синий
Задача 8
Девять осликов за 3 дня съедают 27 мешков корма.
Сколько корма надо пяти осликам на 5 дней?
Решение :
1 шаг 9 осликов в 1 день - 27 : 3= 9м.
2 шаг 1 ослик в 1 день - 9 : 9 = 1 м.
3 шаг 5 осликов в 1 день - 5 * 1 = 5 м.
4 шаг 5 осликов за 5 дней - 5 * 5 = 25 м.
Задача 9
Кенгуру мама прыгает за 1 секунду на 3 метра, а её маленький сынишка прыгает на 1 метр за 0,5 секунды.
Они одновременно стартовали от бассейна к эвкалипту по прямой.
Сколько секунд мама будет ждать сына под деревом, если расстояние от бассейна до дерева 240 метров
Решение :
1 шаг 240 : 3 = 80 (с) скакала мама Кенгуру
2 шаг сын за 0,5 с - 1 м, за 1 с - 2 м
3 шаг 80 * 2 = 160 (м) проскачет кенгурёнок за 80 с
4 шаг 240 - 160 = 80 (м) осталось проскакать кенгурёнку когда
мама уже под эвкалиптом
5 шаг 80 : 2 = 40 (с)
Ответ: 40 секунд.
Задача 10
На скотном дворе гуляли гуси и поросята.
Мальчик сосчитал количество голов, их оказалось 30, а затем он сосчитал количество ног, их оказалось 84.
сколько гусей и сколько поросят было на школьном дворе?
Решение :
1 шаг Представьте, что все поросята подняли по две ноги вверх
2 шаг на земле осталось стоять 30 * 2 = 60 ног
3 шаг подняли вверх 84 - 60 = 24 ноги
4 шаг подняли 24 : 2 = 12 поросят
5 шаг 30 - 12 = 18 гусей
Ответ: 12 поросят и 18 гусей.
ЗАДАЧА 11
Среди 100 одинаковых на вид монет есть несколько фальшивых. Все фальшивые монеты весят одинаково, все настоящие - тоже, фальшивая монета легче настоящей. Имеются также весы (с двумя чашами без стрелки), на каждой чашке умещается только по одной монете. При этом весы слегка испорчены: если монеты разного веса, перевешивает более тяжёлая монета, а если одинакового - перевесить может любая чашка. Как с помощью этих весов найти хотя бы одну фальшивую монету?
Ответ: Разделим монетки на 33 кучки по 3 монетки + 1 монетка.
Каждое трио взвешиваем между собой, получим 3 неравенства, в результате которых увидим, либо каждая монетка будет по одному разу весить меньше от других двух, либо два раза будет весить меньше других двух.
1>2 (возможны такие варианты: н=н, ф=ф, 2-фальшивка)
1<3 (н=н, ф=ф, 1- фальшивка)
2>3 (н=н, ф=ф, 3- фальшивка)
такое возможно, если все три монетки имеют одинаковый вес вежду собой, то есть из них откладываем в сторонку любую одну
1<2(н=н,ф=ф,1-ф)
1<3(н=н,ф=ф,1-ф)
2>3(н=н,ф=ф,3-ф)
У 1 больше вероятностьть оказаться фальшивой, так что ее и откладываем.
И так проделываем с каждой из 33-х кучек, в результате отложим 11 монет +1, которая не попала ни в одну из кучек.
Эти 12 монет опять разделям на 4 кучки по 3 монетки, проделываем те же манипуляции, в результате получим 4 монетки, разделяем на 1 кучку+1, та монетка из кучки, которая окажется легче, вновь откладываем и сравниваем с одинокой монеткой. Та, которая легче и будет фальшивой.
ГЛАВА П Метод графов
Один из способов решения задач типа «Кто есть кто?» - метод графов.
Граф - это несколько точек, часть которых соединены друг с другом отрезками или стрелками (в этом случае граф называется ориентированным).
Рассмотрим метод графов на примере решения задачи:
Жила-была одна дружная семья: мама, папа и сын. Они все любили делать вместе. Но вот мультфильмы любили разные: «Ну, погоди!», «Покемоны», «Том и Джерри». Определите, какой мультфильм любит каждый из них, если мама, папа и любитель мультфильма «Покемоны» никогда не унывают, а папа и любитель мультфильма «Том и Джерри» делают зарядку по утрам?
Решение:
Рассмотрим множество людей: мама, папа, сын и множество мультфильмов «Ну, погоди!», «Покемоны», «Том и Джерри». Обозначим элементы этих двух множеств точками:
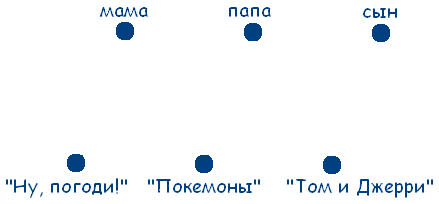
Если точке из одного множества соответствует точка другого множества, будем соединять эти точки сплошной линией, если не соответствует - то штриховой.
Заметим, что по условию задачи у человека только один любимый мультфильм.
Учитывая данные задачи, получаем следующую схему:
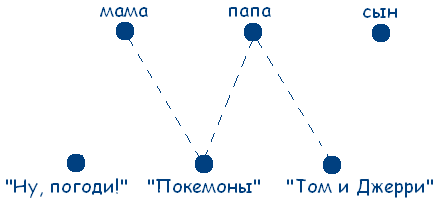
Из условия задачи следует, что нужно найти единственно возможное соответствие между элементами двух множеств.
Правило: если какая-то точка оказывается соединенной с двумя точками другого множества штриховыми линиями, то с третьей точкой она должна быть соединена сплошной.
Поэтому граф на рисунке будет выглядеть следующим образом:
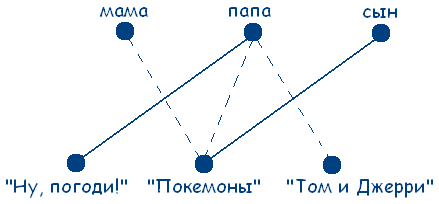
Теперь мы установили, что папа любит мультфильм «Ну, погоди!», сын - «Покемоны». В обеих множествах остается только по одной точке, следовательно мама любит мультфильм «Том и Джерри». Задача решена.
Таким же способом можно находить соответствие между тремя множествами. Тогда при решении мы можем получить треугольники трех видов:
а) все стороны являются сплошными отрезками (решение задачи);
б) одна сторона - сплошной отрезок, а две другие - штриховые;
в) все стороны - штриховые отрезки.
Таким образом, нельзя получить треугольник, у которого бы две стороны были сплошными отрезками, а третья - штриховой отрезок.
Примеры задач:
Задача №1: "Пепси", "Кока-Кола", квас и "Спрайт":
В бутылке, стакане, кувшине и банке находятся «Пепси», «Кока-кола», квас и «Спрайт». Известно, что «Спрайт» и «Пепси» не в бутылке, сосуд с «Кока-колой» находится между кувшином и сосудом с квасом, в банке - не «Кока-кола» и не «Спрайт». Стакан находится около банки и сосуда с «Пепси». Как распределены эти жидкости по сосудам?
Из условий задачи получаем таблицу с запретами:
Сосуд
Бутылка
Стакан
Кувшин
Банка
Жидкость
«Пепси»
-
-
-
«Кока-кола»
-
-
Квас
«Спрайт»
-
-
Так как каждая жидкость находится только в одном сосуде, то в в каждой строчке и каждом столбце может стоять только один «+». Вглянув на таблицу, можно сделать вывод, что «Пепси» в кувшине, а квас в банке. Получаем новую таблицу:
Сосуд
Бутылка
Стакан
Кувшин
Банка
Жидкость
«Пепси»
-
-
+
-
«Кока-кола»
-
-
Квас
-
-
-
+
«Спрайт»
-
-
-
Теперь можно сказать, что «Спрайт» в стакане, а «Кока-кола» в бутылке.
Ответ: Квас в банке; «Пепси» в кувшине; «Кока-кола» в бутылке; «Спрайт» в стакане.
Задача №2: Любители музыки:
В клубе «Отдых» познакомились 3 любителя клубной музыки видов техно, хаус, рейв. Один говорит: «Вы какую музыку больше любите? Я техно люблю!». Другой ответил, что любит хаус, а третий сказал, что не любит ни техно, ни хаус, но зато обожает рейв. Интересно то, что все они были в банданах и рубашках черного, белого и желтого цветов, но цвет банданы и рубашки совпадал только у любителя техно. А у любителя хаус ни рубашка, ни бандана не были белыми. А любитель рейв был в желтой рубашке. Определите цвет рубашек и бандан каждого из любителей клубной музыки.
Заметим, что по условию задачи цвет банданы и рубашки совпадал только у любителя техно. А так как у любителя хаус ни рубашка ни бандана не были белыми и любитель рейв был в желтой рубашке, то делаем вывод, что любитель техно может быть в рубашке и бандане только белого цвета.
Получаем граф:
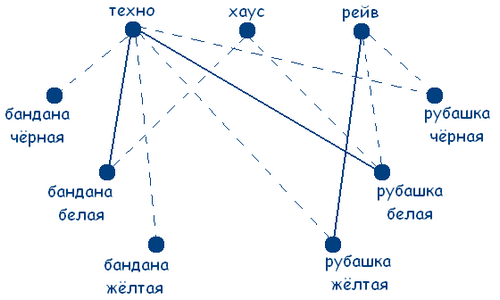
Решение сводится к нахождению трех сплошных треугольников с вершинами в разных множествах. Значит у любителя хаус желтая бандана и черная рубашка (т.к. цвет совпадал только у любителя техно по усл.), а у любителя рейв черная бандана.
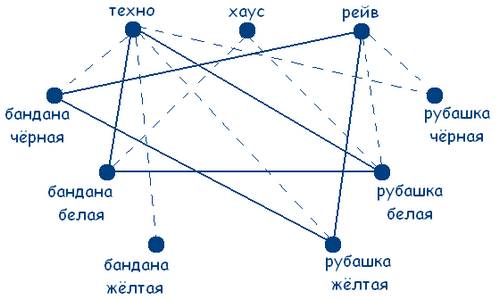
Ответ: У любителя техно рубашка и бандана белого цвета; у любителя хаус черная рубашка и желтая бандана; у любителя рейв желтая рубашка и черная бандана.
Задача №3: Три поросёнка:
Жили-были на свете три поросёнка, три брата: Ниф-Ниф, Наф-Наф, Нуф-Нуф. Построили они три домика: соломенный, деревянный и кирпичный. Все три брата выращивали возле своих домиков цветы: розы, ромашки и тюльпаны. Известно, что Ниф-Ниф живет не в соломенном домике, а Наф-Наф - не в деревянном; возле соломенного домика растут не розы, а тот, у кого деревянный домик, выращивает ромашки. У Наф-Наф аллергия на тюльпаны, поэтому он не выращивает их. Узнайте, кто в каком домике живет и какие цветы выращивает.
Из условий задачи получаем граф:
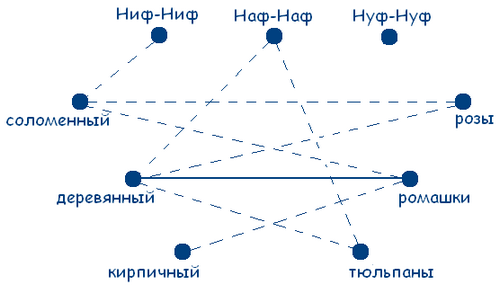
Можно сделать вывод, что возле кирпичного домика растут розы, а возле соломенного - тюльпаны. А так как Наф-Наф живет не в деревянном домике, то он и не выращивает ромашки. А так как на тюльпаны у него аллергия, то он может выращивать только розы. Внесем эти данные в чертеж и получим:
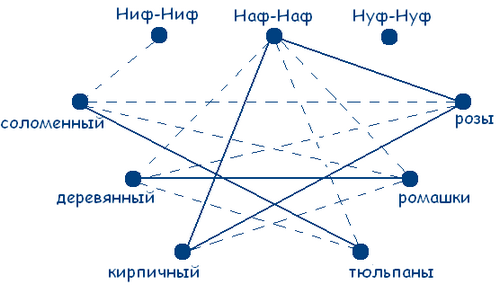
Теперь стало ясно и то, что Ниф-Ниф живет в деревянном домике и выращивает ромашки. Методом исключения получаем, что Нуф-Нуф живет в соломенном домике и выращивает тюльпаны.
Ответ: Наф-Наф живет в кирпичном домике и выращивает розы; Ниф-Ниф живет в деревянном домике и выращивает ромашки; Нуф-Нуф живет в соломенном домике и выращивает тюльпаны.
Задача №4: Компьютерные игры:
В компьютерном классе на уроке информатики, во время отсутствия учителя, пять ребят - Максим, Настя, Саша, Рома, Сережа - отвлеклись от нужной работы и стали играть в такие игры: пасьянс «Паук», гонки, сапер, «Марио», тетрис. Каждый из них играл только в одну игру.
• Саша думал, что в «Марио» играет Настя.
• Настя предполагала, что Рома играет в тетрис, а Максим - в гонки.
• Рома считал, что Сережа играет в гонки, а Саша - в сапера.
• Максим думал, что Настя раскладывает пасьянс «Паук», а в «Марио» играет Рома.
В результате оказалось, что все они ошиблись в своих предположениях. Кто и во что играл?
Таблица с известными запретами (исходя из условия задачи):
Имя
Максим
Настя
Саша
Рома
Сережа
Игра
Пасьянс «Паук»
-
-
Гонки
-
-
-
-
Сапер
-
-
«Марио»
-
-
-
-
тетрис
-
-
Известно, что каждый из игравших играл только в одну, значит, в каждой строке и каждом столбце таблицы может стоять только один «+».
Из условий задачи следует, что Саша не играл в «Марио»; Настя не играла ни в тетрис, ни в гонки; Рома - ни в гонки, ни в сапера; Максим - ни в пасьянс «Паук», ни в Марио.
Так как все предположения ошибочны, то Настя не играет в «Марио», Рома - в тетрис, Максим - в гонки, Сережа - в гонки, Саша - в сапера, Настя - в пасьянс «Паук», Рома - в «Марио».
Используем правило, что если в строке (или столбце) все места, кроме одного, заняты элементарным запретом (знак несоответствия, например «-»), то на свободное место нужно поставить знак «+». В строчке «гонки» можно поставить «+» напротив имени Саша, а в строчке «Марио» напротив имени Сережа. Получаем:
Имя
Максим
Настя
Саша
Рома
Сережа
Игра
Пасьянс «Паук»
-
-
-
-
Гонки
-
-
+
-
-
Сапер
-
-
-
«Марио»
-
-
-
-
+
тетрис
-
-
-
-
Теперь становится ясно, что в пасьянс «Паук» играл Рома, в сапера - Настя, а в тетрис - Максим. Задача решена.
Ответ: Сережа играл в «Марио»; Рома - в пасьянс «Паук»; Саша - в гонки; Настя - в сапера; Максим - в тетрис.
Задача №5: Мушкетёры:
Атос, Портос, Арамис и Д'Артаньян - четыре талантливых молодых мушкетёра. Один из них лучше всех сражается на шпагах, другой не имеет равных в рукопашном бою, третий лучше всех танцует на балах, четвертый без промаха стреляет с пистолетов. О них известно следующее:
• Атос и Арамис наблюдали на балу за их другом - прекрасным танцором.
• Портос и лучший стрелок вчера с восхищением следили за боем рукопашника.
• Стрелок хочет пригласить в гости Атоса.
• Портос был очень большой комплекции, поэтому танцы были не его стихией.
Кто чем занимается?
Таблица с известными запретами:
Занятие
шпажист
рукопашник
танцор
стрелок
Имя
Атос
-
-
Портос
-
-
-
Арамис
-
Д'Артаньян
Известно, что каждый из четырех мушкетеров был лучшим только в одном деле. Следовательно, в каждой строчке и каждом столбце может стоять только один «+». Взглянув на таблицу, сразу можно сказать, что танцор - Д'Артаньян, шпажист - Портос. Вносим эти данные в таблицу. Получаем:
Занятие
шпажист
рукопашник
танцор
стрелок
Имя
Атос
-
-
-
Портос
+
-
-
-
Арамис
-
-
Д'Артаньян
-
-
+
-
Теперь можно сделать вывод, что стрелок - это Арамис, рукопашник - Атос.
Ответ: Арамис - стрелок; Д'Артаньян - танцор; Портос - шпажист; Атос - рукопашник.
ГЛАВА Ш Табличный способ
Табличный способ решения логических задач также прост и нагляден, но его можно использовать только в том случае, когда требуется установить соответствие между двумя множествами. Он более удобен, когда множества имеют по пять-шесть элементов. Рассмотрим табличный способ на примере решения задачи.
Рассмотрим табличный способ на примере решения задачи:
Четыре футбольных команды: итальянская команда «Милан», испанская - «Реал», российская - «Зенит», английская - «Челси» встретились в групповом этапе лиги чемпионов по футболу. Их тренировали тренеры из этих же четырех стран: итальянец Антонио, испанец Родриго, русский Николай, англичанин Джон. Известно, что национальность у всех четырех тренеров не совпадала с национальностью команд. Требуется определить тренера каждой команды, если известно:
а) Зенит не тренируется у Джона и Антонио.
б) Милан обещал никогда не брать Джона главным тренером.
Решение:
Решая задачу, мы заведомо знаем, что у каждой команды только один тренер.
Чтобы решить задачу табличным способом, нужно знать следующие правила:
1.В каждой строке и в каждом столбце таблицы может стоять только один знак соответствия (например «+»).
2.Если в строке (или столбце) все «места», кроме одного, заняты элементарным запретом (знак несоответствия, например «-»), то на свободное место нужно поставить знак «+»; если в строке (или столбце) уже есть знак «+», то все остальные места должны быть заняты знаком «-».
Таким образом, решение будет доведено до конца, когда мы сумеем разместить по одному плюсу в каждом ряду и колонке, обозначив таким образом, тренеров всех четырех команд.
А теперь приступаем к решению задачи.
Нам известно, что ни у одной из команд национальность тренера и команды не совпадали, а также, что «Зенит» не тренируется у Джона и Антонио, значит у этой команды тренер не Джон и не Антонио; а «Милан» обещал никогда не брать Джона тренером, значит у команды «Милан» тренер не Джон. Если проставить соответствующие минусы, то таблица будет выглядеть так:
Команда
Италия - «Милан»
Испания - «Реал»
Россия - «Зенит»
Англия - «Челси»
Тренер
Итальянец
Антонио
-
-
Испанец
Родриго
-
Русский
Николай
-
Англичанин
Джон
-
-
-
Таким образом, становится ясно, что у «Зенита» тренер Родриго (методом исключения). Поставим «+» напротив Родриго в колонке «Зенит» и заполним свободные клетки в его ряду минусами:
Команда
Италия - «Милан»
Испания - «Реал»
Россия - «Зенит»
Англия - «Челси»
Тренер
Итальянец
Антонио
-
-
Испанец
Родриго
-
-
+
-
Русский
Николай
-
Англичанин
Джон
-
-
-
Теперь можно сделать вывод, что тренер «Милана» - Николай. Поставим «+» напротив Николая и заполним свободные клетки в его ряду минусами. Теперь видно, что «Челси» тренирует Антонио, а «Реал» - Джон.
Ответ:
Российская команда «Зенит» тренируется у испанца Родриго; итальянская команда «Милан» тренируется у русского Николая; английская команда «Челси» тренируется у итальянца Антонио; испанская команда «Реал» тренируется у англичанина Марка.
ГЛАВА 1V Задачи на переливание
Рассмотрим еще один тип логических задач. Это задачи на переливания, в которых с помощью сосудов известных емкостей требуется отмерить некоторое количество жидкости.
Все задачи на переливание можно представить двумя типами:
-
«Водолей» - задачи, в которых необходимо получить некоторое количество жидкости с помощью нескольких пустых емкостей из бесконечного источника, из которого можно наливать жидкость, и в который ее можно выливать.
-
«Переливашка» - задачи, в которых необходимо разделить жидкость в большей емкости с помощью нескольких меньших по объему емкостей, жидкость можно только переливать из одной емкости в другую;
Более систематический подход к решению задач «на переливание» заключается в использовании определённой последовательности действий.
В задачах на переливание разрешены следующие операции:
-
заполнение жидкостью одного сосуда до краев;
-
переливание жидкости в другой сосуд или выливание жидкости;
При решении таких задач необходимо учитывать следующие замечания:
-
разрешается наливать в сосуд ровно столько жидкости, сколько в нем помещается;
-
разрешается переливать всю жидкость из одного сосуда в другой, если она в него вся помещается;
-
разрешается отливать из одного сосуда в другой столько жидкости, сколько необходимо, чтобы второй сосуд стал полным.
Каждую задачу на переливание таким методом можно решать двумя способами:
I. начать переливания с большего сосуда;
II. начать переливания с меньшего сосуда.
Какой из способов более рационален (т.е. каким способом мы быстрее получим нужное количество жидкости) зависит от условий задачи. Изначально это определить нельзя.
- При решении задач первого типа («Водолей») можно использовать такой алгоритм. Запишите этот алгоритм в карточку для индивидуальной работы (Приложение 1).
Алгоритм I.
-
Наполнить большую емкость жидкостью из бесконечного источника.
-
Перелить из большей емкости в меньшую емкость.
-
Вылить жидкость из меньшей емкости.
-
Повторить действия 1-3 до тех пор, пока не будет получено обозначенное в условии задачи количество жидкости.
- При решении задач второго типа («Переливашка») можно использовать следующий алгоритм. Запишите этот алгоритм в карточку для индивидуальной работы (Приложение 1).
Алгоритм II.
-
Из большей емкости наполнить емкость промежуточного объема.
-
Перелить жидкость из промежуточной емкости в самую маленькую емкость.
-
Перелить жидкость из самой маленькой емкости в большую емкость.
-
Повторять действия 2-3 до тех пор, пока емкость промежуточного объема не станет пустой.
-
Если емкость промежуточного объема опустела, то повторить действия 1-5 до тех пор, пока не будет получено обозначенное в условии задачи количество жидкости.
ЗАДАЧА Даны 2 кувшина вместимостью 8 и 5 литров. Имеется кран с водой и мойка для слива воды. Как с помощью этих двух кувшинов отмерить ровно 6 литров воды?

Задачу можно оформить в виде следующей таблицы:
1
2
3
4
5
6
7
8
8 л. (А)
0 л.
8 л.
3 л.
3 л.
0 л.
8 л.
6 л.
6 л.
5 л. (B)
0 л.
0 л.
5 л.
0 л.
3 л.
3 л.
5 л.
0 л.
Первый сосуд обозначим через А, а второй - через B.
-
Вначале оба кувшина пусты (первый черный столбец).
-
Наполним водой кувшин А (второй столбец),
-
а затем перельем из него воду в кувшин В (третий столбец).
-
Потом эти 5 литров из кувшина В выльем в раковину (четвертый столбец).
-
Затем 3 литра воды из кувшина А перельем в кувшин В (пятый столбец).
-
Вновь наполним кувшин А водой из под крана (шестой столбец)
-
и дольем из него в кувшин В 2 литра, наполнив его до краев (седьмой столбец столбец).
-
Выливаем из кувшина В содержимое в раковину (восьмой столбец) - задача решена
Рассмотрим примеры решения задач:
Задача № 1 : Однажды Винни-Пух захотел полакомиться медом и пошел к пчелам в гости. По дороге нарвал букет цветов, чтобы подарить труженицам пчелкам. Пчелки очень обрадовались, увидев мишку с букетом цветов, и сказали: «У нас есть большая бочка с медом. Мы дадим тебе меда, если ты сможешь с помощью двух сосудов вместимостью 3 л и 5 л налить себе 4 л!» Винни-Пух долго думал, но все-таки смог решить задачку. Как он это сделал?
Решение:
Как в результате можно получить 4 л? Нужно из 5-литрового сосуда отлить 1 л. А как это сделать? Нужно в 3-литровом сосуде иметь ровно 2 л. Как их получить? - Из 5-литрового сосуда отлить 3 л.
Решение лучше и удобнее оформить в виде таблицы:
Ходы
1
2
3
4
5
6
5 л
5
2
2
-
5
4
3 л
-
3
-
2
2
3
Наполняем из бочки 5-литровый сосуд медом (1 шаг). Из 5-литрового сосуда отливаем 3 л в 3-литровый сосуд (2 шаг). Теперь в 5-литровом сосуде осталось 2 литра меда. Выливаем из 3-литрового сосуда мед назад в бочку (3 шаг). Теперь из 5-литрового сосуда выливаем те 2 литра меда в 3-литровый сосуд (4 шаг). Наполняем из бочки 5-литровый сосуд медом (5 шаг). И из 5-литрового сосуда дополняем медом 3-литровый сосуд. Получаем 4 литра меда в 5-литровом сосуде (6 шаг). Задача решена.
Поиск решения можно было начать с такого действия: к трем литрам добавить 1 литр.
Но тогда решение будет выглядеть следующим образом:
Ходы
1
2
3
4
5
6
7
8
5 л
-
3
3
5
-
1
1
4
3 л
3
-
3
1
1
-
3
-
Задача № 2: Бэтмен и Человек-Паук:
Бэтмен и Человек-Паук никак не могли определить, кто из них самый главный супергерой. Что только они не делали: отжимались, бегали 100 метровку, подтягивались - то один победит, то другой. Так и не разрешив свой спор, отправились они к мудрецу. Мудрец подумал и сказал: «Самый главный супергерой - это не тот, кто сильнее, а тот, кто сообразительнее! Вот, кто решит первым задачу, тот и будет самым-самым! Слушайте: имеются два сосуда вместимостью 8 л и 5 л. Как с помощью этих сосудов налить из источника 7 л живой воды?» Помогите вашему любимому герою решить эту задачу.
Ход рассуждений таков:
Как в результате получить 7 литров? - Нужно к 5 литрам долить 2 л. А где их взять? - Из 5-литрового сосуда отлить 3 л. А как их получить? В 8 литровый перелить из 5 литрового 5 литров, потом еще три.
Решение задачи показано в таблице:
Ходы
1
2
3
4
5
6
7
8 л
-
5
5
8
-
2
7
5 л
5
-
5
2
2
5
-
Задача № 3: Губка Боб:
Губке Бобу срочно нужно налить из водопроводного крана 6 л воды. Но он имеет лишь два сосуда 5-литровый и 7-литровый. Как ему это сделать?
Решение задачи представлено в таблице:
Ходы
1
2
3
4
5
6
7
8
9
10
7 л
7
2
2
-
7
4
4
-
7
6
5 л
-
5
-
2
2
5
-
4
4
5
Задача № 4 Гарри Поттер:
У Гарри Потера имеются двое песочных часов: на 7 минут и на 11 минут. Волшебное зелье должно варится 15 минут. Как сварить его Гарри Потеру, перевернув часы минимальное количество раз?
15 = (11 - 7) + 11. Нужно одновременно перевернуть часы, через 7 минут Гарри начинаем варить зелье. После 4 минут (песок в часах на 11 минут закончится) вновь перевернуть часы на 11 минут.Задача решена.
Задача № 5 Запасливый Винни-Пух:
Летом Винни-Пух сделал запас меда на зиму и решил разделить его пополам, чтобы съесть половину до Нового Года, а другую половину - после Нового года. Весь мед находится в ведре, которое вмещает 6 литров, у него есть 2 пустые банки - 5-литровая и 1-литровая. Может ли он разделить мед так, как задумал?
Представлено в таблице:
Ходы
1
2
3
4
5
6
6 л
6
1
1
2
2
3
5 л
-
5
4
4
3
3
1 л
-
-
1
-
1
-
Задача № 6 Карлсон и варенье:
У Карлсона есть ведро варенья, оно вмещает 7 литров. У него есть 2 пустых ведерка - 4-литровое и 3-литровое. Помогите Карлсону отлить 1 литр варенья к чаю в меньшее (3-литровое) ведерко, оставив 6 литров в большом (7-литровом) ведре.
Представлено в таблице:
Ходы
1
2
3
4
7 л
7
3
3
6
4 л
-
4
1
1
3 л
-
-
3
-
Задача № 7
Отмерить 3 л, имея сосуд 5 л.
Какое наименьшее число переливаний потребуется для того, чтобы в четырехлитровую кастрюлю с помощью крана и пятилитровой банки налить 3 литра воды?
Решение
Наливаем кастрюлю.
Переливаем воду из кастрюли в банку.
Наливаем кастрюлю.
Доливаем полную банку, и в кастрюле остается 3 литра.
Задача № 8
Деление 10 л поровну, имея сосуды 3, 6 и 7 л.
Разделить на 2 равные части воду, находящуюся в 6-литровом сосуде (4 л) и в 7-литровом (6 л), пользуясь этими и 3-литровым сосудами.
Какое наименьшее количество переливаний потребуется?
Решение задачи 2.
В скобках - второй вариант решения.
Сосуд 6 л
Сосуд 3 л
Сосуд 7 л
До переливания
4
0
6
Первое переливание
1 (4)
3 (3)
6 (3)
Второе переливание
1 (6)
2 (1)
7 (3)
Третье переливание
6 (2)
2 (1)
2 (7)
Четвертое переливание
5 (2)
3 (3)
2 (5)
Пятое переливание
5 (5)
0 (0)
5 (5)
Задача № 9.
Деление 8 л поровну, имея сосуды 8, 5 и 3 л.
Разделить на две равные части воду, находящуюся в полном 8 литровом сосуде, пользуясь этим и пустыми 5- и 3-литровыми сосудами.
Какое наименьшее количество переливаний потребуется?
Решение :
Сосуд 8 л
Сосуд 5 л
Сосуд 3 л
До переливания
8
0
0
Первое переливание
3
5
0
Второе переливание
3
2
3
Третье переливание
6
2
0
Четвертое переливание
6
0
2
Пятое переливание
1
5
2
Шестое переливание
1
4
3
Седьмое переливание
4
4
0
Задача № 10:.
Деление 16 л поровну, имея сосуды 6, 11 и 16 л.
Разделить на две равные части воду, находящуюся в полном 16 литровом сосуде, пользуясь этим и пустыми 11- и 6-литровыми сосудами.
Какое наименьшее количество переливаний потребуется?
Сосуд 16 л
Сосуд 11 л
Сосуд 6 л
До переливания
16
0
0
Первое переливание
10
0
6
Второе переливание
10
6
0
Третье переливание
4
6
6
Четвертое переливание
4
11
1
Пятое переливание
15
0
1
Шестое переливание
15
1
0
Седьмое переливание
9
1
6
Восьмое переливание
9
7
0
Девятое переливание
3
7
6
Десятое переливание
3
11
2
Одиннадцатое переливание
14
0
2
Двенадцатое переливание
14
2
0
Тринадцатое переливание
8
2
6
Четырнадцатое переливание
8
8
0
Задача № 11.
Два сосуда и кран с водой.
Какое наименьшее число переливаний необходимо для того, чтобы с помощью 7- и 11-литровых сосудов и крана с водой отмерить 2 л?
Если сначала наполнить 11-литровый сосуд, то потребуется 18 переливаний, а если 7-литровый, то, как следует из рисунка, - всего 14.

Задачи "на переливание" более чем увлекательные. Один из методов их решения - "от конца к началу". Нужно исходить из того, что надо получить.
Задача № 12. Как, пользуясь банками в 3 л и 5 л, набрать воды ровно 1 л?
Решение:
Сосуды
Переливания
5 литров
-
3
3
5
3 литра
3
-
3
1
Задача № 13 Как отмерить 4 л воды с помощью сосудов в 3 л и 5 л?
Решение:
Сосуды
Переливания
5 литров
-
3
3
5
-
1
1
4
3 литра
3
-
3
1
1
-
3
-
Задача № 14 . Как, имея лишь два сосуда емкостью 5 л и 7 л, отмерить 6 л воды?
Решение:
Сосуды
Переливание
7 литров
7
2
2
-
7
4
4
-
7
6
5 литров
-
5
-
2
2
5
-
4
4
5
Задача № 15 Набрать 7 л воды из речки.
У подножья высокого холма, на берегу тихой речки был небольшой аул. Жили в нем два брата-охотника. Старшего брата звали Каалка, младшего Копчон. Отправляет старший брат младшего за водой и дает ему два бурдюка, вместимостью 8л и 5л и просит принести ровно 7л воды. Сможет ли Копчон выполнить просьбу старшего брата?
Решение:
-
Ходы
1
2
3
4
5
6
7
8л
-
5
5
8
-
2
7
5л
5
-
5
2
2
5
-
Задача № 15. Молоко из Простоквашино.
Дядя Федор собрался ехать к родителям в гости и попросил у кота Матроскина 4 л простоквашинского молока. А у Матроскина только 2 пустых бидона: трехлитровый и пятилитровый. И восьмилитровое ведро, наполненное молоком. Как Матроскину отлить 4 литра молока с помощью имеющихся сосудов?
Решение:
Переливаем из 8-литрового ведра 5 литров молока в 5-литровое. Переливаем из 5-литрового бидона 3 литра в 3-литровый бидон.
Переливаем их теперь в 8-литровое ведро. Итак, теперь 3-литровое ведро пусто, в 8-литровом 6 литров молока, а в 5-литровом - 2 литра молока.
Переливаем 2 литра молока из 5-литрового бидона в 3-литровый, а потом наливаем 5 литров из 8-литрового ведра в 5-литровый бидон. Теперь в 8-литровом 1 литр молока, в 5-литровом - 5, а в 3-литровом - 2 литра молока.
Доливаем дополна 3-литровый бидон из 5-литрового и переливаем эти 3 литра в 8-литровое ведро. В 8-литровом ведре стало 4 литра, так же, как и в 5-литровом бидоне. Задача решена.
сосуд 8 л
сосуд 5 л
сосуд 3 л
До переливания
8
0
0
Первое переливание
3
5
0
Второе переливание
3
2
3
Третье переливание
6
2
0
Четвертое переливание
6
0
2
Пятое переливание
1
5
2
Шестое переливание
1
4
3
Седьмое переливание
4
4
0
После переливания, оказалось, по 4 л молока в 8-литровом и 5-литровом сосудах, а это и требовалось.
Задача № 16 Переливание
Имеется 3 сосуда: 8л 5л 3л.
Первый из них заполнен водой.
Нужно оставить ровно 4л. в первом сосуде.
8л 5л 3л
8л 5л 3л
8 0 0
3 5 0
3 2 3
6 2 0
6 0 2
1 5 2
1 4 3
4 4 0
8 0 0
5 0 3
5 3 0
2 3 3
2 5 1
7 0 1
7 1 0
4 1 3
Задача № 17 : Как отметить 4л воды с помощью сосудов в 3л и 5 л?
-
сосуды
переливания
5 литров
-
3
3
5
-
1
1
4
3 литра
3
-
3
1
1
-
3
-
Задача № 18 : Как, имя лишь два сосуда емкостью 5л и 7 л, отметить6л воды?
-
сосуды
переливания
7 литров
7
2
2
-
7
4
4
-
7
6
5 литра
-
5
-
2
2
5
-
4
4
5
.Задача № 19:
Каким образом из реки можно принести ровно 6л воды, если имеется только два ведра: одно - емкостью 4л. другое - 9л?
-
сосуды
переливания
9 литров
9
5
5
1
1
-
9
6
4 литра
-
4
-
4
-
1
1
4
Задача № 20: Бидон емкостью 10л заполнен молоком. Требуется перелить из этого бидона 5л в семилитровый бидон, используя при этом еще один бидон, вмещающий 3л.
-
сосуды
переливания
10 литров
3
3
6
6
9
9
2
2
7 литров
7
4
4
1
1
-
7
5
3 литра
-
3
-
3
-
1
1
3
Задача № 21: Имея два бидона емкостью 4л и 5л, можно ли налить в ведро 3л воды. Если емкость ведра не менее 3л?
-
сосуды
переливания
5 литров
-
4
4
5
5
4 литров
4
-
4
3
-
3 литра и более
-
-
-
-
3
Задача № 22: (задача Пуассона) Известному французскому математику Симону Пуассону(1981-1840) в юности предложили задачу. Заинтересовавшись ею, Пуассон затем увлекся математикой и посвятил этой науке всю свою жизнь. Вот эта задача. Некто имеет 12 пинт вина и хочет отлить из этого количества половину, но у него нет сосуда в 6 пинт. Зато есть два других сосуда: в 8 пинт и 5 пинт. Спрашивается: каким образом налить 6 пинт в сосуд на 8 пинт?
-
сосуды
переливания
12 пинт
12
4
4
9
9
1
1
6
8 пинт
-
8
3
3
-
8
6
6
5 пинт
-
-
5
-
3
3
5
-
Задача № 23 :
Как, имея два ведра 14 и 15 литров, набрать из реки 7 литров воды?
Убедитесь что с помощью этих ведер можно набрать любое количество литров,
выраженное натуральным числом меньше 14.
Набрали 15 литров и перелили из ведра в 14-литровое.
стало
1
14
осталось
1
вылили всё 0
перелили из 1-го во 2-е
0
1
набрали
15
1
перелили 13л во 2-е
2
1+13=14
2
вылили 0
перелили 2 литра
0
2
набрали в первое
15
2
перелили 12 во 2-е
3
2+12=14 - вылили
3
0
И так далее. В большом ведре получили 1 литр, затем 2, затем 3 литра.
Продолжая дальше наливать и переливать, получим любое целое количество литров от 1 до 15.
Алгоритм такой: сначала оба ведра пустые.
1. В пустое первое набираем из реки 15 литров.
2. Во второе переливаем из первого (сколько поместится).
3. Из второго выливаем в реку.
4. В пустое второе выливаем то, что осталось в первом.
5. Переходим на пункт 1
Задача № 24 : Имеются три бочонка вместимостью 6 вёдер, 3 ведра и 7 вёдер. В первом и третьем содержится соответственно 4 и 6 ведёр кваса. Требуется, пользуясь только этими тремя бочонками, разделить квас поровну.
Ответ: Решение 1:
Бочонки
Шестиведерный
Трехведерный
Семиведерный
До переливания
4
0
6
После 1-го переливания
1
3
6
После 2-го переливания
1
2
7
После 3-го переливания
6
2
2
После 4-го переливания
5
3
2
После 5-го переливания
5
0
5
Решение 2:
Бочонки
Шестиведерный
Трехведерный
Семиведерный
До переливания
4
0
6
После 1-го переливания
4
3
3
После 2-го переливания
6
1
3
После 3-го переливания
2
1
7
После 4-го переливания
2
3
5
После 5-го переливания
5
0
5
Задача № 25:
Двое должны разделить поровну 8 ведер кваса, находящегося в восьмиведерном бочонке. Но у них есть только два пустых бочонка, в один из которых входит 5 ведер, а в другой - 3 ведра. Спрашивается, как они могут разделить этот квас, пользуясь только этими тремя бочонками?
Ответ: Приведем два решения в виде двух таблиц.
Решение 1:
Бочонки
Восьмиведерный
Пятиведерный
Трехведерный
До переливания
8
0
0
После 1-го переливания
3
5
0
После 2-го переливания
3
2
3
После 3-го переливания
6
2
0
После 4-го переливания
6
0
2
После 5-го переливания
1
5
2
После 6-го переливания
1
4
3
После 7-го переливания
4
4
0
Решение 2:
Бочонки
Восьмиведерный
Пятиведерный
Трехведерный
До переливания
8
0
0
После 1-го переливания
5
0
3
После 2-го переливания
5
3
3
После 3-го переливания
2
3
1
После 4-го переливания
2
5
1
После 5-го переливания
7
0
0
После 6-го переливания
7
1
3
После 7-го переливания
4
1
0
После 8-го переливания
4
4
Задача № 26:
Имеются шестилитровая банка сока и две пустые банки: трех- и четырехлитровая. Как налить 1 литр сока в трехлитровую банку?
Ответ: Приведем одно из возможных решений в виде таблицы:
Банки
6 л
4 л
3 л
До переливания
6
0
0
После 1-го переливания
2
4
0
После 2-го переливания
2
1
3
После 3-го переливания
5
1
0
После 4-го переливания
5
0
1
Задача № 27:
Винодел обычно продает свое вино по 30 и по 50 литров и использует для этого кувшины только такого размера. Один из покупателей захотел купить 10 литров. Как винодел отмерил ему 10 литров пользуясь своими кувшинами?
Ответ: Сначала он наполнил 30-литровый кувшин и вылил его содержимое в 50-литровый. Потом опять наполнил 30-литровый и долил до полного заполнения в 50-литровый. В результате у него в кувшине останется 10 литров.
Задача № 28 :
Три человека купили сосуд, полностью заполненный 24 унциями бальзама. Позже они приобрели три пустых сосуда объемом 5, 11 и 13 унций. Как они могли бы поделить бальзам на равные части используя эти четыре сосуда? Постарайтсь решить задачу за наименьшее количество переливаний.
Ответ. Сосуды могут содержать 24, 13, 11, и 5 унций соответственно:
Их начальное состояние 24, 0, 0, 0;
1 - 8, 0, 11, 5;
2 - 8, 11, 0, 5;
3 - 8, 13, 3, 0;
4 - 8, 8, 3, 5;
5 - 8, 8, 8, 0.
Текст задачи
Решение
У нас имеется водопроводный кран и раковина, куда можно сливать воду. Как отмерить 4 литра воды с помощью пустых сосудов в 3л и 5л?
1 сосуд (3л)
2 сосуд (5л)
0 (пустой)
5 (налили из крана)
3 (перелили из 2-го сосуда 3л)
2
0 (вылили в раковину 3л)
2
2 (перелили из 2-го сосуда 2л)
0 (пустой)
2
5 (налили из крана)
3 (долили доверху из 2-го сосуда)
4 (осталось после переливания)
Текст задачи
Решение
У нас имеется водопроводный кран и раковина, куда можно сливать воду. Как отмерить 1 литра воды с помощью пустых сосудов в 3л и 5л?
1 сосуд (3л)
2 сосуд (5л)
3 (налили из крана)
0 (пустой)
0 (пустой)
3 (перелили из 1-го сосуда 3л)
3 (налили из крана)
3
1(осталось после переливания)
5 (перелили из 1-го сосуда 2л)
Текст задачи
Решение
Бидон, емкость которого 10л, наполнен водой. Имеются еще пустые сосуды в 7л и 2л. Как разлить воду в два сосуда поровну (т.е по 5л в каждый)?
1 сосуд (10л)
2 сосуд (7л)
3 сосуд (2л)
10 (полный)
0 (пустой)
0 (пустой)
3
7 (перелили из 1-го
сосуда 7 л)
0 (пустой)
3
5
2 (перелили из 2-го
сосуда 2 л)
5 (перелили из 3-го
сосуда 2 л)
5
0 (пустой)
Еще несколько задач на переливание для самостоятельного решения:
-
Для разведения картофельного пюре быстрого приготовления "Зеленый великан" требуется 1 л воды. Как, имея два сосуда емкостью 5 и 9 литров, налить 1 литр воды из водопроводного крана?
-
Для марш-броска по пустыне путешественнику необходимо иметь 4 литра воды. Больше он взять не может. На базе, где имеется источник воды, выдают только 5-литровые фляги, а также имеются 3-литровые банки. Как с помощью одной фляги и одной банки набрать 4 литра во флягу?
-
В походе приготовили ведро компота. Как, имея банки, вмещающие 500г и 900г воды, отливать компот порциями по 300 г?
-
Нефтяники пробурили скважину нефти. Необходимо доставить в лабораторию на экспертизу 6 литров нефти. В распоряжении имеется 9-литровый и 4-литровый сосуды. Как с помощью этих сосудов набрать 6 литров?
-
Как с помощью двух бидонов емкостью 17 литров и 5 литров отлить из молочной цистерны 13 литров молока?
-
К продавцу, стоящему у бочки с квасом, подходят два веселых приятеля и просят налить им по литру кваса каждому. Продавец замечает, что у него есть лишь две емкости в 3 л и 5 л, и поэтому он не может выполнить их просьбу. Приятели продолжают настаивать и дают продавцу 100 рублей с одним условием, что они получат свои порции одновременно. После некоторого размышления продавец сумел это сделать. Каким образом?
-
Взгляни на берег - там ты увидишь две банки. В одну из них помещается ровно два литра воды, а в другую - три. Как налить в двухлитровую банку точно один литр? Укажи два способа.
-
Располагая двухлитровым и пятилитровыми банками, сделай так, чтобы в одном из них оказался ровно литр воды.
-
Возьми две стеклянные банки. В одну из них, наполненную до краёв, помещается один литр воды, а в другую - два. Как сделать так, чтобы в двухлитровой банке оказался точно один литр? Сделай это различными способами.
-
Задача - шутка. Перед тобой двухлитровый и трёхлитровый банки, а также девятилитровая тяжелая бочка. Как бы ты не старался с помощью банок налить в нее ровно один литр воды, у тебя ничего не получится. Как думаешь, почему? Дай хотя бы один верный ответ.
-
Поставили самовар, а потом 7 раз садились пить чай и каждый раз выпивали половину имеющейся в нем воды. Оказалось, что после этого остался всего стакан воды. Сколько воды было в самоваре перед чаепитием?
-
Поставили самовар, а потом 7 раз садились пить чай и каждый раз выпивали половину имеющейся в нем воды и еще полстакана, после чего воды не осталось. Сколько воды было в самоваре перед чаепитием?
-
Имеются две одинаковые чашки, одна с чаем, а другая - пустая. Из первой переливают половину имеющегося в ней чая во вторую, затем из второй переливают треть имеющегося в ней чая в первую, затем из первой переливают четверть имеющегося в ней чая во вторую и т.д. Сколько чая окажется в каждой из чашек после 100 переливаний?
-
В два достаточно больших бидона как-то разлили 3 л воды. Из первого переливают половину имеющейся в нем воды во второй, затем из второго переливают половину имеющейся в нем воды в первый, затем из первого переливают половину имеющейся в нем воды во второй и т.д. Докажите, что независимо от того, сколько воды было сначала в каждом из сосудов, после 100 переливаний в них будет 2 л и 1 л с точностью до миллилитра.
-
Тому Сойеру нужно покрасить забор. Он имеет 12 л краски и хочет отлить из этого количества половину, но у него нет сосуда вместимостью в 6 л. У него 2 сосуда: один - вместимостью в 8 л, а другой - вместимостью в 5 л. Каким образом налить 6 л краски в сосуд на 8 л? Какое наименьшее число переливаний необходимо при этом сделать?
-
Две группы альпинистов готовятся к восхождению. Для приготовления еды они используют примусы, которые заправляют бензином. В альплагере имеется 10-литровая канистра бензина. Имеются еще пустые сосуды в 7 и 2 литров. Как разлить бензин в два сосуда по 5 литров в каждом?
-
Как разделить поровну между двумя семьями 12 литров хлебного кваса, находящегося в двенадцатилитровом сосуде, воспользовавшись для этого двумя пустыми сосудами: 8-литровым и 3-литровым?
-
Летом Винни Пух сделал запас меда на зиму и решил разделить его пополам, чтобы съесть половину до Нового Года, а другую половину - после Нового года. Весь мед находится в ведре, которое вмещает 6 литров, у него есть 2 пустые банки - 5-литровая и 1-литровая. Может ли он разделить мед так, как задумал?
-
Белоснежка ждет в гости гномов. Зима выдалась морозной и снежной, и Белоснежка не знает наверняка, сколько гномов решатся отправиться в далекое путешествие в гости, однако знает, что их будет не более 12. В ее хозяйстве есть кастрюлька на 12 чашек, она наполнена водой, и две пустых - на 9 чашек и на 5. Можно ли приготовить кофе для любого количества гостей, если угощать каждого одной чашкой напитка?
-
Нефтяники пробурили скважину нефти. Необходимо доставить в лабораторию на экспертизу 6 литров нефти. В распоряжении имеется 9-литровый и 4-литровый сосуды. Как с помощью этих сосудов набрать 6 литров?
-
Бидон ёмкостью 10 л наполнен молоком. Требуется перелить из этого бидона 5 л в семилитровый бидон, используя при этом ещё один бидон, вмещающий 3 л. Как это сделать?
-
Можно ли отмерить 8 л воды, находясь у реки и имея два ведра: одно вместимостью 15 л, другое вместимостью 16 л?
-
Есть три бидона емкостью 14, 9 и 5 литров. В большом бидоне 14 л молока, остальные пусты. Как с помощью этих бидонов разделить молоко пополам?
-
Имея два полных десятилитровых бидона молока и пустые четырехлитровую и пятилитровую кастрюли, отмерьте по два литра молока в каждую кастрюлю.
-
Имеется три сосуда без делений объемами 6 л, 7 л, 8 л, кран с водой, раковина и 6л сиропа в самом маленьком сосуде. Можно ли с помощью переливаний получить 12 л смеси воды с сиропом, так чтобы в каждом сосуде воды и сиропа было поровну?
-
Двое должны разделить поровну 8 вёдер кваса, находящегося в большом бочонке. Но у них есть ещё только два пустых бочонка, в один из которых входит 5 вёдер, а в другой - 3 ведра. Спрашивается, как они могут разделить этот квас, пользуясь только этими тремя бочонками? Решите задачу двумя способами.
-
Как, имея пятилитровое ведро и девятилитровую банку, набрать из реки ровно три литра воды?
ГЛАВА V Задачи на взвешивание
Задачи на взвешивания - достаточно распространенный вид математических задач. В таких задачах от решающего требуется локализовать отличающийся от остальных предмет по весу за ограниченное число взвешиваний. Поиск решения в этом случае осуществляется путем операций сравнения, правда, не только одиночных элементов, но и групп элементов между собой.
Рассмотрим этот метод на примере решения задач:
Задача № 1 У Буратино есть 27 золотых монет. Но известно, что Кот Базилио заменил одну монету на фальшивую, а она по весу тяжелее настоящих. Как за три взвешивания на чашечных весах без гирь Буратино определить фальшивую монету?
Решение:
Ответ: Сумма чисел в каждой строке должна равняться 16. Разделим монеты на 3 кучки по 9 монет. Положим на чаши весов первую и вторую кучки; по результату этого взвешивания мы точно узнаем, в какой из кучек находится фальшивка (если весы покажут равенство, то она - в третьей кучке). Теперь, аналогично, разделим выбранную кучку на три части по три монеты, положим на весы две из этих частей и определим, в какой из частей находится фальшивая монета. Наконец, остается из трех монет определить более тяжелую: кладем на чаши весов по 1 монете - фальшивкой является более тяжелая; если же на весах равенство, то фальшивой является третья монета из части. Задача решена.
Задача № 2 : Среди 101 одинаковых по виду монет одна фальшивая, отличающаяся по весу. Как с помощью чашечных весов без гирь за два взвешивания определить, легче или тяжелее фальшивая монета? Hаходить фальшивую монету не требуется.
Решение:
Взвешиваем 50 и 50 монет: два случая.
1 случай: Равенство. Берем оставшуюся монету и ставим ее в левую кучку вместо одной из имеющихся там:
а) Левая кучка тяжелее => фальшивая монета тяжелее;
б) Левая кучка легче => фальшивая монета легче.
2 случай: Неравенство. Берем более тяжелую кучку и разбиваем ее на две кучки по 25 монет:
а) Вес кучек одинаковый => фальшивая монета легче;
б) Вес кучек неодинаковый => фальшивая монета тяжелее.
Задача № 3 : Фальшивая монета:
Имеется 8 монет. Одна из них фальшивая и легче настоящей монеты. Определите за 3 взвешивания какая из монет фальшивая.
Делим монеты на две равные кучки - по 4 монеты в каждой. Взвешиваем. Ту кучку, которая легче, опять делим на две одинаковых кучки - теперь по две монеты в каждой. Взвешиваем. Определяем, какая из них легче. Кладем на чаши весов по 1 монете из этой кучки. Фальшивая та, которая легче. Задача решена.
Задача № 4 : Фальшивая монета:
Имеется 10 монет. Одна из них фальшивая и легче настоящей монеты. Как, с помощью чашечных весов без гирь, определить какая из монет фальшивая?
Разделим 10 монет на 2 равных кучки - по 5 монет. Положим на чаши весов. Определим, в какой из этих кучек находится фальшивая монета. Теперь эту кучку делим на 3 кучки - в двух из них по две монеты, в третьей одна монета. Взвешиваем кучки, в которых по две монеты. Если весы покажут равенство, то фальшивка в третьей кучке. Если покажут неравенство, то фальшивая монета в кучке, которая легче. Теперь кладем на чаши весов по 1 монете из этой кучки - фальшивкой является более легкая. Задача решена.
Задача № 5 : Лиса Алиса и Кот Базилио:
Лиса Алиса и Кот Базилио - фальшивомонетчики. Базилио делает монеты тяжелее настоящих, а Алиса - легче. У Буратино есть 15 одинаковых по внешнему виду монет, но какая-то одна - фальшивая. Как двумя взвешиваниями на чашечных весах без гирь Буратино может определить, кто сделал фальшивую монету - Кот Базилио или Лиса Алиса?
Буратино может разделить свои монеты на три кучки по 7, 4, 4, или по 5, 5, 5, или по 3, 6, 6, или по 1, 7, 7 монет. При первом взвешивании он положит на весы две кучки монет одинаковой величины. Если при этом весы оказались в равновесии, значит, все монеты на весах настоящие, а бракованная монета в оставшейся кучке. Тогда при втором взвешивании на одну чашку весов Буратино положит кучку с бракованной монетой, а на вторую - столько настоящих монет, сколько всего монет он положил на первую чашку, и тогда он сразу определит, легче фальшивая монета, чем настоящие, или тяжелее. Если же при первом взвешивании весы оказались не в равновесии, значит, все монеты в оставшейся кучке настоящие. Тогда Буратино уберет с весов легкую кучку, а монеты из тяжелой кучки разделит на две равные части и положит на весы (если в кучке было 5 или 7 монет, предварительно добавит к ним одну настоящую монету). Если при втором взвешивании весы оказались в равновесии, значит, фальшивая монета легче настоящих, а если нет, то тяжелее. Задача решена.
Задача № 6 :
Имеются 6 гирь весом 1, 2, 3, 4, 5 и 6 г. На них нанесена соответствующая маркировка. Однако есть основания считать, что при маркировке гирь допущена одна ошибка. Как при помощи двух взвешиваний на чашечных весах, на которых можно сравнить веса любых групп гирь, определить, верна ли имеющаяся на гирях маркировка?
Ответ: На одну чашу весов кладем гири, маркированные 1, 2 и 3 г., а на другую - 6 г. Равновесие означает, что ошибка в маркировке возможна лишь внутри групп 1-2-3 и 4-5. При втором взвешивании на одну чашу кладем гири 3 и 5 г., на другую - 6 и 1 г. Если первая чаша перевесила, то ошибки а маркировке нет.
Задача № 7 :
Имеется 8 с виду одинаковых монет. Одна из них фальшивая и известно, что она легче настоящей. Как с помощью всего лишь двух взвешиваний найти фальшивую монету? В Вашем распоряжении только лабораторные весы, которые показывают только больше-меньше.
Ответ: Делим монеты на две равные кучки. Из каждой кучки берем по 3 монеты, кладем на весы и взвешиваем. Если вес одинаковый то взвешиваем оставшиеся 1и 1 монеты и выявляем фальшивую (более легкую). Если же одна группа из трех монет легче другой, значит там есть фальшивая монета. Оставляем более легкую группу из трех монет и кладем на весы 1и 1 и действуем по предыдущему алгоритму: если вес одинаков, значит фальшива третья, а если нет то та которая легче.
Задача № 8
Как развесить 20 фунтов чая в 10 коробок по 2 фунта в каждой за девять развесов, имея только гири на 5 и на 9 фунтов? Используются обычные весы с двумя чашами - как у статуи Правосудия
Ответ: 1) Hа одну чашу весов положить гирю в 5 фунтов, на другую гирю в 9 фунтов. Затем уравновесить весы, насыпав 4 фунта чая в чашу с гирей на 5 фунтов.
2) Убрать гири с чаш весов, оставить 4 фунта в одной чаше и уравновесить весы, насыпав во вторую еще 4 фунта.
3) Еще раз отвесить 4 фунта.
4) И еще раз 4 фунта. Таким образом, после четырех взвешиваний в остатке будет тоже 4 фунта.
5-9) Разделить 4 фунта пополам, уравновешивая чаши весов.
Задача № 9
У есть 8 внешне одинаковых гирек весом 1 г, 2 г, 3 г, ..., 8 г. Он помнит, какая из гирек сколько весит, но граф Склероз ему не верит. Сможет ли барон провести одно взвешивание на чашечных весах, в результате которого будет однозначно установлен вес хотя бы одной из гирь?
Ответ: Да. 7+8 = 1+2+3+4+5, остается 6.
Задача № 10 :
На столе лежит десять пронумерованных шляп. В каждой шляпе лежит по десять золотых монет. В одной из шляп находятся фальшивые монеты. Настоящая весит 10 граммов, а поддельная только 9. В помощь даны весы со шкалой в граммах. Как определить в какой из шляп находятся фальшивые монеты, используя весы только для одного взвешивания? Весы могут взвешивать не более 750 грамм.
Ответ: Легко! Из первой шляпы берем 1 монету, из второй - 2, из третьей - 3 и т.д. Все это взвешиваем и отнимаем результат от идеального веса (в нашем случае 55*10=550 грамм). Получившееся число будет совпадать с номером шляпы с фальшивыми монетами.
Задача № 11 : У Буратино есть 27 золотых монет. Но известно, что Кот Базилио заменил одну монету на фальшивую, а она по весу тяжелее настоящих. Как за три взвешивания на чашечных весах без гирь Буратино определить фальшивую монету?
Решение: Разделим монеты на 3 кучки по 9 монет. Положим на чаши весов первую и вторую кучки; по результату этого взвешивания мы точно узнаем, в какой из кучек находится фальшивка (если весы покажут равенство, то она - в третьей кучке). Теперь, аналогично, разделим выбранную кучку на три части по три монеты, положим на весы две из этих частей и определим, в какой из частей находится фальшивая монета. Наконец, остается из трех монет определить более тяжелую: кладем на чаши весов по 1 монете - фальшивкой является более тяжелая; если же на весах равенство, то фальшивой является третья монета из части. Задача решена.
ГЛАВА V1 Задания на восстановление записей вычислений
Условие математического ребуса содержит либо целиком зашифрованную запись (цифры заменены буквами), либо только часть записи (стертые цифры заменены точками или звездочками).
Записи восстанавливаются на основании логических рассуждений. При этом нельзя ограничиваться отысканием только одного решения. Испытание нужно доводить до конца, чтобы убедиться, что нет других решений, или найти все решения. Есть математические ребусы, имеющие несколько решений.
Математический ребус - задание на восстановление записей вычислений.
Математические ребусы обычно используются для развития у школьников, поскольку их решение построено на логических рассуждениях.
Математические ребусы бывают нескольких видов, например:
-
Цифры в записи вычисления заменены буквами. В таких ребусах необходимо восстановить всю запись.
-
Некоторые цифры в записи стёрты, вместо них поставлены «звездочки». В таких ребусах необходимо восстановить часть записи.
Некоторые математические ребусы имеют несколько вариантов решения. При разгадывании математических ребусов обычно условием ставится проверка всех возможных вариантов.
№ 1 :Задача
Восстановите поврежденную запись
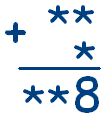
Ответ. 99 + 9 = 108
Задача № 2
Восстановите поврежденную запись

Ответ. 99 + 99 = 198
Задача № 3 :
Решите ребус:

Решение:
Очевидно, Д≤4. В разряде сотен имеем А + А = А, значит, А = 0 (без перехода) или А = 9 (с переходом). Значение А = 0 не подходит, так как в разряде единиц А + А = Р (получаем А = Р = 0). Значит, А = 9, Р = 8, Е = 7. Тогда 2М + 1 = 10 + Т, Т < 9, значит М = 5 или 6 (так как получается переход), а значения 7 и 8 уже заняты буквами Е и Р. При М = 6 получается решение:
18969 + 18969 = 37938.
Ответ:18969 + 18969 = 37938.
Задача № 4 Решите ребус:

Так как КА + КА + КА оканчивается на КА, то КА = 50, а значит, К = 5, А = 0. Так как Ш + Ш + Ш + 1 оканчивается на 0, то Ш = 3.
Так как сумма трех чисел, начинающихся на 5 может начинаться лишь с 1, то С = 1.
Рассматривая варианты для О, получаем, что О = 6 или О = 7, а значит, Б = 9 или Б = 2.
Итак, получаем два варианта решения:
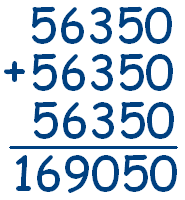 и
и 
-
Задача № 5 Решите ребус:

Ответ: С = 4; П = 3; Т = 2; Р = 7; К = 8; О = 9.

Задача № 6 Решите ребус, если известно, что наибольшая цифра
в числе СИЛЕН равна 5.
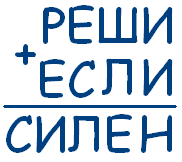
Так как наибольшая цифра в числе «СИЛЕН» равна 5, а С = 1, то остальные 4 цифры в данном числе будут 2, 3, 4, 5.
Так как Н < 6, то И = 2. А значит, Н = 4. Так как Л > Е (в самом деле так как Е + 1 = Л, то Л > Е, ведь Л и Е меньше 5 по условию), то Л = 5, Е = 3.
А тогда уже легко находим остальные цифры: Ш = 8, Р = 9.
В итоге получается: 9382 + 3152 = 12534
Ответ: 9382 + 3152 = 12534
Задача № 7 Решите ребус
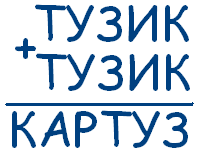
Ответ.54271 + 54271 = 108542
Задача № 8 Решите ребус

-
Ответ.3930 + 3980 = 7910 (начать с А = 0, К < 5, так как О + О = О и О ≠ А, то О = 9. Рассматривая К = 1, 2, 3, 4, получим искомое решение).
ГЛАВА У1 ОЛИМПИАДНЫЕ ЗАДАЧИ:
1. Решите задачу (7 баллов)
На пиратском рынке бочка рома стоит 800 дублонов, или 100 пиастров, а пистолет стоит 100 дублонов, или 250 дукатов. Сколько пиастров нужно заплатить за попугая, если за него просят 100 дукатов?
Ответ: 5 пиастров
2. Решите задачу (7 баллов)
Три синих попугая капитана Флинта съедают 3кг. корма за три дня, пять зеленых попугаев - 5кг. корма за пять дней, а семь оранжевых - 7кг. корма за семь дней. Какие попугаи самые прожорливые?
-
-
За один день три синих съедают - 1кг. корма, пять зеленых и семь оранжевых тоже съедают в день по 1кг корма.
-
Ответ: Синие попугаи самые прожорливые.
3. Решите задачу (7 баллов)
Крепость имеет вид семиугольника, в каждой вершине которого находится сторожевая башня. Каждую из семи стен крепости охраняют стражники в башнях, находящихся в концах этой стены. Какое наименьшее количество стражников нужно разместить в башнях, чтобы каждая стена охранялась не менее чем семью стражниками?
Комментарии по оцениванию: Занумеруем башни подряд 1, 2, 3,…,7.
Тогда в первой башне находится х1 стражник, во второй - х2 стражник, … в седьмой - х7 стражник. Каждая стена охранялась не менее чем семью стражниками, значит,
х1+х2 <7, х2+х3 >7 и т.д. Складывая эти неравенства, получим: 2(х1+х2+…+х7) > 49, отсюда (х1+х2+…+х7) > 49:2, поскольку число стражников целое, то оно не может быть меньше 25.
Ответ: 25.
4. Решите задачу (7 баллов)
Пират испортил карту сокровищ, имеющую форму квадрата. Он вырезал из неё восьмиугольник, а 5 отрезанных многоугольников выбросил. Оставшейся восьмиугольник имеет стороны равной длины, и внутренние углы равной величины.
а) Можно ли по этому восьмиугольнику восстановить размеры карты сокровищ?
б) Определите, какую форму могли иметь 5 отрезанных многоугольников.
-
-
Комментарии по оцениванию:
-
а) Можно ли по этому восьмиугольнику восстановить размеры карты сокровищ? (3 балла)
-
б) Определите, какую форму могли иметь 5 отрезанных многоугольников. (за каждый приведенный пример 2 балла)
-
Так как оставшийся кусок имеет форму правильного восьмиугольника, а отрезанных кусков - 5, то они могут иметь не больше одной общей стороны со стороной восьмиугольника. Значит, минимум три стороны восьмиугольника принадлежат квадрату. Поэтому форма искомой карты сокровищ будет квадрат со стороной, равной расстоянию между противоположными сторонами восьмиугольника. Отрезанные многоугольнику будут: 1) 5 треугольников; 2) 4 треугольника и один четырехугольник.
5. Решите задачу (7 баллов)
Робинзон попал на необитаемый остров. Каждый день (начиная с того дня, когда он попал на остров) он вырезал на доске первую букву в названии дня недели на русском языке. На 2013-й день, вырезав букву, он посчитал вырезанные буквы. Оказалось, что разных букв было вырезано разное количество. В ответ запишите день недели, когда Робинзон попал на остров.
В течение недели Робинзон вырежет на доске по две буквы «п» (понедельник, пятница), «в» (вторник, воскресенье), «с» (среда, суббота) и одну букву «ч» (четверг). Так как 2013=287·7+4=2009+4, то через 2009 дней будет вырезано по 574 буквы «п», «в», «с» и 287букв «ч». Через четыре дня количества букв оказались различными. Для этого нужно, чтобы в эти четыре дня одна из букв «п», «в», «с» появилась дважды, одна - один раз и одна не появлялась. Значит, четвертой появившейся буквой должна быть «ч». Буквы идут в следующем порядке: «п», «в», «с», «ч», «п», «с», «в», «п», «в», «с» …
Таким образом, возможна лишь ситуация: «с», «ч», «п». Это означает, что Робинзон попал на остров в среду.
Ответ: среда
Задачи по математике для 5 - 6 класса с конкурса «Кенгуру» :
Задача № 1 На день рождения пришло двенадцать детей следующих возрастов: 6 лет, 7 лет, 8 лет, 9 лет и 10 лет, причем четырем детям было по 6 лет, а восьмилетних было больше всех. Вычислите их средний возраст.
Решение: Так как число детей младшего возраста равно 4, то число восьмилетних может быть не менее 5. Если их больше 5, то шести и восьмилетних будет больше 9. Тогда на детей возрастов 7 лет, 9 лет и 10 лет останется в сумме только или 1 год или 2 года. Этого быть не может. Значит восьмилетних детей ровно 5 человек. Остаток от 12 составит 3 ребенка. Их надо распределить между возрастами 7 лет, 9 лет и 10 лет. Легко понять, что их ровно по одному человеку.
Получаем следующий расклад: 6 лет - 4 человека; 7 лет - 1 человек; 8 лет - 5 человек; 9 лет - 1 человек;10 лет - 1 человек.
Найдем теперь средний возраст - среднее арифметическое имеющихся возрастов. Напомню, что средним арифметическим нескольких чисел называют результат деления их суммы на их количество. Вычисляем его так: ( 6*4 + 7*1 + 8*5 + 9*1 + 10*1) / 12 = 7,5
Ответ: 7,5 лет.
-
Задача № 2 :
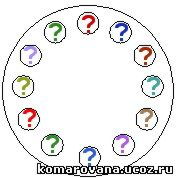
Натуральные числа от 1 до 12 расставлены по кругу. Разность любых двух соседних равна 1 или 2. Укажите числа, которые стоят рядом.
А) 5 и 6
Б) 10 и 9
В) 8 и 10
Г) 6 и 7
Д) 4 и 3
Возьмем старт с единицы: 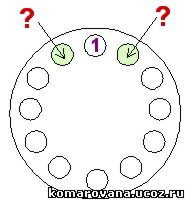
Очевидно, что соседями единички являются числа 2 и 3. Из-за того, что симметричные расклады дают один и тот же ответ, 2 и 3 можно расставить вокруг числа 1 произвольным образом. Запишем, например, слева 2, а справа 3.
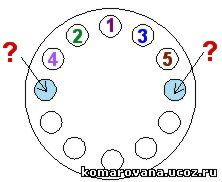 Соседним числом д
Соседним числом д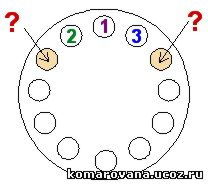 ля 2, расположенным в выделенном кружке слева, может быть только число, большее чем 2 (меньшая единица уже задействована). Это 3 или 4. Так как 3 не должно повториться, имеем единственный вариант продолжения - направить число 4 в выделенный правый кружок.У числа 3 вторым соседом будет или 4 или 5. Число 5 повторно использовать нельзя, поэтому единственной возможностью остается постановка сила 5.
ля 2, расположенным в выделенном кружке слева, может быть только число, большее чем 2 (меньшая единица уже задействована). Это 3 или 4. Так как 3 не должно повториться, имеем единственный вариант продолжения - направить число 4 в выделенный правый кружок.У числа 3 вторым соседом будет или 4 или 5. Число 5 повторно использовать нельзя, поэтому единственной возможностью остается постановка сила 5.
Продолжая таким же образом далее получаем окончательно распределение: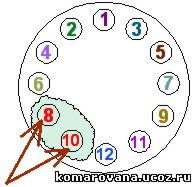
Ответ: 8 и 10.
Задачи по математике для 5 класса с конкурса «МЕЖДУНАРОДНАЯ ДИСТАНЦИОННАЯ МАТЕМАТИЧЕСКАЯ ОЛИМПИАДА «ТРЕТЬЕ ТЫСЯЧЕЛЕТИЕ»»
Задача №1
Расставьте в клетках квадрата ![]() одну единицу, две двойки,
одну единицу, две двойки, ![]() тройки,
тройки, ![]() четверки,
четверки, ![]() пятерок и еще одну любую цифру по своему выбору так, чтобы во всех строках получилась одна и та же сумма цифр.
пятерок и еще одну любую цифру по своему выбору так, чтобы во всех строках получилась одна и та же сумма цифр.
5
4
3
4
5
4
2
5
1
3
9
3
5
5
2
4
.Задача №2
Расположите на плоскости ![]() спичек так, чтобы они образовали как можно больше различных квадратов. Укажите в ответе число этих квадратов.
спичек так, чтобы они образовали как можно больше различных квадратов. Укажите в ответе число этих квадратов.
____________ - размер спички.
-
25 квадратов
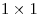 ;
; -
16 квадратов
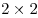 ;
; -
9 квадратов
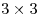 ;
; -
4 квадрата
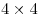 ;
; -
1 квадрат
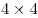 .
.
![]() .
.
Ответ: 55 квадратов.
.Задача №3:
Аня хочет положить в каждую коробку одинаковое число своих игрушек. Сначала она попыталась разложить их по 12 в каждую коробку, но 5 игрушек оказались лишними. Затем она попробовала разложить их по 15 в каждую коробку, но для последней коробки остались только 2 игрушки. Тогда Аня догадалась взять еще одну коробку. Сколько игрушек Аня должна теперь положить в каждую коробку, чтобы добиться своей цели?
Пусть ![]() - количество тугриков у Васи. Тогда,
- количество тугриков у Васи. Тогда, ![]() - стоимость 39 солдатиков;
- стоимость 39 солдатиков; ![]() - стоимость 35 солдатиков. Значит, 4 солдатика стоят
- стоимость 35 солдатиков. Значит, 4 солдатика стоят ![]() тугрика. 1 солдатик стоит
тугрика. 1 солдатик стоит ![]() тугриков. У Васи было
тугриков. У Васи было ![]() тугриков.
тугриков.
Задача №4
Из книги выпал кусок, первая страница которого имеет номер 143, а номер последней состоит из тех же цифр, но записанных в другом порядке. Сколько страниц выпало из книги?
Задача №5
Три яблока, четыре груши и один персик стоят 40 руб. Одно яблоко, четыре груши и персик стоят 32 руб. Сколько стоят одно яблоко, одна груша и один персик, если персик стоит столько, сколько стоят два яблока?
Задача №6
Кенгуру мама прыгает за 1 секунду на 3 метра, а её маленький сынишка прыгает на 1 метр за полсекунды. Они одновременно стартовали от бассейна к эвкалипту по прямой. Сколько секунд мама будет ждать сына под деревом, если расстояние от бассейна до дерева 240 метров? (40 секунд)
Задача №7
Найдите периметр и площадь прямоугольника со сторонами 6 см и 8 см.
Задача №8
Используя переместительное и сочетательное свойства умножения, упростить:
11•х•30
Задача №9
Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть:
А) слагаемое
В) вычитаемое
С) число 10
D) известное частное
E) разность
Задача №10
В три банки с надписями «малиновое», «клубничное» и «малиновое или клубничное» налили смородиновое, малиновое и клубничное варенье. Все надписи оказались неправильными. Какое варенье налили в банку «клубничное»?
Задача №11
Коробку размером 30 х 30 х 50 нужно наполнить одинаковыми кубиками.
Какое минимальное количество кубиков позволит это сделать?
A) 15
B) 30
C) 45
D) 75
E) 150
Задача №12
Задания для школьной олимпиады: примеры и выражения. В записи (88888888) нужно поставить знаки сложения таким образом, чтобы получилась сумма, которая будет равна 1000.
Задача №13
В ящике лежат шары: 5 красных, 7 синих и 1 зелёный. Сколько шаров надо вынуть, чтобы достать два шара одного цвета?
Ответы к задачам
Задача 4
172 страницы
Задача 5 груша стоит 5 рублей, яблоко - 4 рубля, персик - 8 рублей
Задача 6
4 руб.
8 руб.
5 руб.
Задача 7
28 см и 48 см²
В пещере старый пират разложил свои сокровища в 3 цветных сундука, стоящих вдоль стены: в один - драгоценные камни, а в другой - золотые монеты, а в третий - оружие. Он помнит, что :
- красный сундук правее, чем драгоценные камни
- оружие правее, чем красный сундук.
В сундуке какого цвета лежит оружие, если зелёный сундук стоит левее, чем синий?
Решение :
ДК - зелёный
ЗC - красный
330x
Задача 8
вариант E
Задача 9
Так как все надписи неправильные, то в третьей банке не может быть ни малиновое, ни клубничное варенье. Значит, там смородиновое варенье. Тогда клубничное и малиновое должны быть в первых двух банках. А так как надписи неправильные, то в банке «клубничное» на самом деле малиновое варенье.
Задача 10
вариант C
Задача 11
Способ 1: 88+8+8+8+888=1000
Способ 2: 8+8+888+88+8=1000
Задача 12
надо вынуть 4 шара
Задача 13:
О - синий
Задача1 4 :
Девять осликов за 3 дня съедают 27 мешков корма.
Сколько корма надо пяти осликам на 5 дней?
Решение :
1 шаг 9 осликов в 1 день - 27 : 3= 9м.
2 шаг 1 ослик в 1 день - 9 : 9 = 1 м.
3 шаг 5 осликов в 1 день - 5 * 1 = 5 м.
4 шаг 5 осликов за 5 дней - 5 * 5 = 25 м.
Задача 15 :
Кенгуру мама прыгает за 1 секунду на 3 метра, а её маленький сынишка прыгает на 1 метр за 0,5 секунды.
Они одновременно стартовали от бассейна к эвкалипту по прямой.
Сколько секунд мама будет ждать сына под деревом, если расстояние от бассейна до дерева 240 метров
Решение :
1 шаг 240 : 3 = 80 (с) скакала мама Кенгуру
2 шаг сын за 0,5 с - 1 м, за 1 с - 2 м
3 шаг 80 * 2 = 160 (м) проскачет кенгурёнок за 80 с
4 шаг 240 - 160 = 80 (м) осталось проскакать кенгурёнку когда
мама уже под эвкалиптом
5 шаг 80 : 2 = 40 (с)
Ответ: 40 секунд.
Задача 16 :
На скотном дворе гуляли гуси и поросята.
Мальчик сосчитал количество голов, их оказалось 30, а затем он сосчитал количество ног, их оказалось 84.
сколько гусей и сколько поросят было на школьном дворе?
Решение :
1 шаг Представьте, что все поросята подняли по две ноги вверх
2 шаг на земле осталось стоять 30 * 2 = 60 ног
3 шаг подняли вверх 84 - 60 = 24 ноги
4 шаг подняли 24 : 2 = 12 поросят
5 шаг 30 - 12 = 18 гусей
Ответ: 12 поросят и 18 гусей.
Задача 17
Инженер ежедневно приезжал на станцию в одно и то же время, и в то же время за ним подъезжала машина, на которой он ехал на завод.
Однажды инженер приехал на станцию на 55 мин раньше обычного.
Сразу пошел навстречу машине и приехал на завод на 10 мин раньше, чем обычно.
Во сколько раз скорость инженера меньше скорости машины?
Решение:
За 10 мин машина проходит путь, равный двойному расстоянию от станции до места встречи инженера с машиной.
Значит, путь от станции до места встречи машина проходит за 5 мин.
На месте встречи машина была за 5 мин до времени обычного приезда инженера на станцию, значит, путь от станции до места встречи инженер шел 55 мин - 5 мин = 50 мин.
Следовательно, скорость инженера в 50 : 5 = 10 раз меньше скорости машины.
Задача 18
В триседьмом царстве живут драконы.
У каждого дракона одна, две или три головы,
а) Может ли у 40 % драконов быть 60 % голов?
б) Может ли у 40 % драконов быть 70 % голов?
Решение:
а) Покажем, что у 40% драконов может быть 60% голов.
Пусть в этом царстве живет 100 драконов: 40 драконов с одной головой, 20 - с двумя головами и 40 - с тремя.
Тогда число голов у всех драконов равно
40 • 1 + 20 • 2 + 40 • 3 = 200.
При этом все 40 трехглавых драконов, что составляет 40% от общего числа драконов, имеют 40 • 3 = 120 голов, что составляет
120/200 • 100% = 60% от общего числа голов.
б) Пусть число драконов равно х, а общее число голов у них равно у.
Предположим, что какие-то 40% драконов имеют 70% голов.
Тогда, поскольку каждый из этих драконов имеет не более трех голов, то 0,7у = 3 • 0,4х.
С другой стороны, поскольку остальные 60% драконов имеют 30% голов и у каждого из них не менее одной головы, то 0,6х = 0,3y.
Но эти неравенства не могут выполняться одновременно, так как они равносильны соответственно 7у = 12х и 12x = 6у.
Поэтому у 40% драконов не может быть 70% голов.
Задача 19
В пещере старый пират разложил свои сокровища в 3 цветных сундука, стоящих вдоль стены: в один - драгоценные камни, а в другой - золотые монеты, а в третий - оружие. Он помнит, что :
- красный сундук правее, чем драгоценные камни
- оружие правее, чем красный сундук.
В сундуке какого цвета лежит оружие, если зелёный сундук стоит левее, чем синий?
Решение :
ДК - зелёный
ЗC - красный
О - синий
Задача 20
Девять осликов за 3 дня съедают 27 мешков корма.
Сколько корма надо пяти осликам на 5 дней?
Решение :
1 шаг 9 осликов в 1 день - 27 : 3= 9м.
2 шаг 1 ослик в 1 день - 9 : 9 = 1 м.
3 шаг 5 осликов в 1 день - 5 * 1 = 5 м.
4 шаг 5 осликов за 5 дней - 5 * 5 = 25 м.
Задача 21
Кенгуру мама прыгает за 1 секунду на 3 метра, а её маленький сынишка прыгает на 1 метр за 0,5 секунды.
Они одновременно стартовали от бассейна к эвкалипту по прямой.
Сколько секунд мама будет ждать сына под деревом, если расстояние от бассейна до дерева 240 метров
Решение :
1 шаг 240 : 3 = 80 (с) скакала мама Кенгуру
2 шаг сын за 0,5 с - 1 м, за 1 с - 2 м
3 шаг 80 * 2 = 160 (м) проскачет кенгурёнок за 80 с
4 шаг 240 - 160 = 80 (м) осталось проскакать кенгурёнку когда
мама уже под эвкалиптом
5 шаг 80 : 2 = 40 (с)
Ответ: 40 секунд.
Задача 22
На скотном дворе гуляли гуси и поросята.
Мальчик сосчитал количество голов, их оказалось 30, а затем он сосчитал количество ног, их оказалось 84.
сколько гусей и сколько поросят было на школьном дворе?
Решение :
1 шаг Представьте, что все поросята подняли по две ноги вверх
2 шаг на земле осталось стоять 30 * 2 = 60 ног
3 шаг подняли вверх 84 - 60 = 24 ноги
4 шаг подняли 24 : 2 = 12 поросят
5 шаг 30 - 12 = 18 гусей
Ответ: 12 поросят и 18 гусей.
ЗАДАЧА 23
Часы Юры отстают на 8 минут, но он считает, что часы спешат на 2 минуты. Часы Коли спешат на 2 минуты, однако он думает, что они отстают на 8 минут. Друзья договорились, что встретиться в 5 часов вечера. Кто раньше окажется у места встречи и на сколько минут
РЕШЕНИЕ: Отметим, что мальчики приходят в точку встречи по своему «внутреннему» таймеру (который рассчитывают), а не по реальному. Поэтому надо узнать, каково реальное время в момент прихода каждого. Найдем разницу между реальным временем и тем временем, которое представляет себе Юра. Пусть точное время x минут, тогда на часах Юры x-8 минут. Так как он думает, что они спешат, значит считает, что сейчас x-8-2 минут. Поэтому значение реального времени больше того, которое представляет себе Юра на 10 минут. Это означает, что к моменту прихода Юры в точку встречи реальное время составит 17ч 10 мин.
Аналогично рассуждая можно получить расклад по Коле. Пусть y (мин) - реальное время. Тогда часы Коли в этот момент показывают y+2 (мин). Так как он думает, что часы отстают на 8 минут, значит считает, что в этот момент y+2+8 минут.
Поэтому значение реального времени меньше представляемого Колей на 10 минут. Это значит, что к моменту прихода Коли реально 16ч 50 мин. Поэтому Коля пришел раньше Юры на 20 минут.
ЗАДАЧА 24
Петя в трамвае заметил Васю, который поравнялся с трамваем следуя вдоль трамвайных путей в противоположном направлении. Через минуту Петя вышел и побежал вдогонку за Васей вдвое быстрее его, но в 4 раза медленнее трамвая. Через какое время Петя догонит Васю? Помогите.
РЕШЕНИЕ: Прежде всего, нужно понять, что означает «в два раза быстрее». Это значит, что скорость больше в два раза. А поэтому в два раза больше будет пройденное расстояние (не важно, за какое время). Тогда, если Петя идет в два раза быстрее Васи и в 4 раза медленнее трамвая, то Вася проходит за минуту в ![]() раз меньшее расстояние, чем трамвай.
раз меньшее расстояние, чем трамвай.
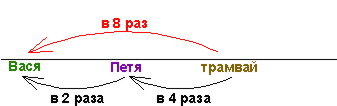 Поэтому если за одну минуту Вася проходит какой-то отрезок пути, то трамвай проезжает 8 таких отрезков. Поэтому расстояние между мальчиками в момент выхода Пети составляет 9 отрезков. За ту же минуту Петя проходит 2 отрезка (раз его скорость в 2 раза больше). Введем единицу измерения длины, равную этому же отрезку. Тогда мы имеем стандартные начальные данные для самой обычной задачи на скорость сближения. Скорости мальчиков известны - это 1 (отрезок/мин) и 2 (отрезка/мин), а расстояние для сближения составляет 9 отрезков.
Поэтому если за одну минуту Вася проходит какой-то отрезок пути, то трамвай проезжает 8 таких отрезков. Поэтому расстояние между мальчиками в момент выхода Пети составляет 9 отрезков. За ту же минуту Петя проходит 2 отрезка (раз его скорость в 2 раза больше). Введем единицу измерения длины, равную этому же отрезку. Тогда мы имеем стандартные начальные данные для самой обычной задачи на скорость сближения. Скорости мальчиков известны - это 1 (отрезок/мин) и 2 (отрезка/мин), а расстояние для сближения составляет 9 отрезков.
За каждую минуту оно сокращается на 2-1=1 отрезок (это и есть скорость сближения). А нам надо узнать, за какое время расстояние в 9 отрезков сократится до нуля, то есть надо узнать время сближения. Его можно найти, разделив путь сближения на скорость сближения. Поэтому 9 делим на 1 и получаем 9 минут. Ответ: 9 мин.
ЗАДАЧА 25
Cвете втрое больше лет, чем было Максиму тогда, когда она была в его нынешнем возрасте. Когда Максим будет в возрасте Светы, то им вместе будет 28лет. Сколько сейчас лет Максиму и сколько сейчас лет Свете?
РЕШЕНИЕ: Запутанные (олимпиадные) задачи на возраст удобно показывать на временной оси, на которой возраста представляются точками. Если у нас 2 человека и их возраста меняются, то изображающие их точки будут просто двигаться по оси. При этом расстояние между ними (разница в возрасте) будет сохраняться. Покажем нынешний возраст Светы и Максима точками С и М (верхний ряд букв на рисунке). В нижнем ряду поставим буквы С и М для того момента, когда «Света была в нынешнем возрасте Максима». Получим равные отрезки, концы которых (нижняя М и верхняя С) согласно условию «в 3 раза» можно обозначить как х и 3х. Тогда нынешний возраст Максима (середина отрезка) будет иметь координату 2х, а значит разница в возрасте составит ровно х (лет). Теперь покажем, какими будут координаты возрастов в тот момент, когда Максим окажется в возрасте Светы. Эти буквы стоят в ряду «будущее». Длина их отрезка тоже равна х (лет) и поэтому возраст Светы в этот момент окажется равным 4х (лет). Так как в будущем им вместе будет 28 лет, то 3х+4х=28, откуда получаем, что х=4. Поэтому Максиму сейчас ![]() лет, а Свете сейчас
лет, а Свете сейчас ![]() лет.
лет.
ЗАДАЧА 26:
решить олимпиадную задачку за 5 - 6 класс. Вася написал в тетради 4 числа. Сложил их по два всеми возможными способами получил шесть таких сумм: 2, 4, 9, 9, 14, 16. Какие числа записал Вася?
РЕШЕНИЕ: Пусть a, b, с, d - искомые числа, расположенные в порядке возрастания. Составим последовательность их суммы также в порядке возрастания используя неравенство a < b < c < d. Получим такой ряд:
1) a+b=2
2) a+c=4
3,4) b+c и a+d
5) b+d=14
6) c+d=16
Первые две суммы явно наименьшие и поэтому равны 2 и 4. Две последние явно наибольшие и равны соответственно 14 и 16. Осталось выяснить судьбу двух оставшихся: b+с и a+d. Но так на них приходятся две девятки, то каждая из них равна 9. По первым двум суммам делаем вывод, что с на 2 больше чем b. Поэтому c=b+2. Подставляя выражение для числа с в равенство b+c=9 получим, что b+b+2=9. Поэтому b=3,5 и значит c=3,5+2=5,5. Из первого равенства вытекает, что a=2-3,5=-1,5, а из последнего, что d=16-5,5=10,5
В итоге ответ оказывается таким: -1,5; 3,5; 5,5 и 10,5
ЗАДАЧА 27
Всего 5555 человек, на 10 солдат приходится 1 капрал, на 5 капралов 1 офицер, на 9 офицеров 1 генерал. Решение: сколько всего было солдат?
РЕШЕНИЕ:
Для начала определим, сколько человек в одном таком «наборе», состоящем из генерала, капралов, офицеров и солдат.
Один генерал и девять офицеров у нас уже есть. Так как на каждого офицера приходится 5 капралов, то на 9 офицеров приходится ![]() капралов.
капралов.
Так как на каждого капрала приходится 10 солдат, то на 45 капралов приходится ![]() солдат.
солдат.
Всего человек в «наборе» ![]()
Так как всего в армии 5555 человек, то количество «наборов» равно
![]() . В одном «наборе»
. В одном «наборе» ![]() солдат, поэтому в 11 «наборах» будет
солдат, поэтому в 11 «наборах» будет ![]() солдат.
солдат.
Ответ: ![]() солдат.
солдат.
Задача 28
. В несколько одинаковых автобусах 115 человек поехали на озеро, 138 - в лес. Все места в автобусах были заняты, и всем хватило места. Сколько было заказано автобусов и сколько мест в каждом автобусе? (1)
Решение:
Поскольку мест в автобусах не осталось, число детей, выехавших в каждом из двух направлений, кратно числу мест в автобусе. Следовательно, число мест в автобусе - общий делитель чисел 115 и 138. Для отыскания общего делителя воспользуемся правилом : общий делитель двух чисел является также общим делителем этих чисел и их разности.
138 - 115 = 23. Всего автобусов с детьми было:
(115 + 138)/23 = 11 автобусов.
Ответ: 11 автобусов
Задача 28
. Как при помощи только пяти цифр 5, знаков арифметических действий и скобок представить каждое из чисел от 0 до 10 включительно?(1)
Решение. Например:
-
0=(5-5)*(5+5+5)
-
1=5:5+(5-5)*5
-
2=(5+5):5+5-5
-
3=(5*5-5-5):5
-
4=5-5:5+5-5
-
5=5+(5-5)*(5+5)
-
6=5+5:5+5-5
-
7=5+5:5+5:5
-
8=5+(5+5+5):5
-
9=(5*5-5):5+5
-
10=5+5+(5-5)*5
Задача 29
. После 7 стирок длина, ширина и высота куска хозяйственного мыла, имеющего форму прямоугольного параллелепипеда, уменьшились вдвое. На сколько стирок хватит оставшегося мыла?(1)
Решение:
Нарисовав кусок мыла и поделив каждую сторону пополам, видим, что получится 8 маленьких кусочков, каждый из которых равен оставшемуся после 7 стирок. То есть на 7 стирок ушло мыла столько, сколько было в остальных 7 кусочках, поэтому остатка хватит ровно на одну стирку.
Ответ. Оставшегося мыла хватит на одну стирку.
Задача 30
. Четыре утёнка и пять гусят весят 4 килограмма 100 грамм, а пять утят и четыре гусенка весят 4 килограмма. Сколько весит 1 утенок? (3)
Решение:
4утенка + 5 гусят=4100грамм
5утят + 4гусят =4000, значит 9 утят и 9 гусят весят 8100 грамм, 1 утенок и 1 гусенок 8100:9=900 грамм, тогда 4 утят и 4 гусят 900*4=3600 грамм, 4000-3600=400 грамм весит 1 утенок
Ответ: 400 грамм
Задача 5. Решите числовой ребус (3)
ОДИН
+
ОДИН
-
МНОГО
Решение: Очевидно, О число чётное, но 2*О больше, чем 10 и поэтому О=6 или О=8, если О =8, то Н=4 и 2*О <15( а должно быть 2*О=16) поэтому, О=6, Н=3, М=1, Д >5 и 2Д=16, значит, Д=8. 2И=Г и И ≤4, но И≠1, так, как М=1; И≠3 или Н=3 И≠4, иначе, Г=Д=8, И≠0, иначе Г=О. тогда И=2, Г=4, получаем
6823
+
6823
________________
13646
Задача 31
. Имеются бревна разной длины. Когда каждое из них распилили на несколько частей, то оказалось, что частей получилось на 25 больше, чем было сделано распилов. Сколько брёвен было первоначально?
Решение: Если бревно распилить на любое число частей , то частей всегда окажется больше, чем распилов. Если частей получилось на 25 больше, чем было распилов, значит, первоначально брёвен было 25.
Ответ: 25
Задача 32
. В день рождения дяди Федора почтальон Печкин хочет выяснить, сколько тому лет. Шарик говорит, что дяде Федору больше 11 лет, а кот Матроскин утверждает, что больше 10 лет. Сколько лет дяде Федору, если известно, что ровно один из них ошибся? Ответ обоснуйте.
Решение: Заметим, что если не ошибся Шарик, то не ошибся и Матроскин, что противоречит условию. Значит, Шарик сказал неправду, в отличие от кота Матроскина. Таким образом, дяде Федору больше 10 лет, но не меньше 11., дяде Федору исполнилось 11 лет.
Ответ: 11 лет.
Задача 33
.Математическая логика .(6)
Когда три подруги - Надя, Валя и Маша - вышли гулять, на них были белое, красное и синее платья. Туфли их были тех же трех цветов, но только у Нади цвета туфель и платья совпадали. При этом у Вали ни платье, ни туфли не были синими, а Маша была в красных туфлях. Определите цвет платьев и туфель каждой из подруг.
Подсказка
У Вали белые туфли - почему?
Решение:
У Вали туфли не синие (по условию) и не красные (красные - у Маши), следовательно, у Вали белые туфли; у Нади, таким образом, оставшиеся синие. Это в свою очередь означает, что у Нади - синее платье (по условию, цвета туфель и платья у Нади совпадают). Тогда у Вали - красное платье, а у Маши - белое (поскольку у них по условию туфли и платья разного цвета, причём не синего, так как всё синее - на Наде). Итак: у Нади туфли и платье синего цвета; у Вали туфли белые, платье красное; у Маши туфли красные, платье белое. 1
Ответ: У Нади туфли и платье синего цвета; у Вали туфли белые, платье красное; у Маши туфли красные, платье белое.
Задача 34
В комнате находятся 85 воздушных шаров - красных и синих. Известно, что: 1) по крайней мере один из шаров красный; 2) из каждой произвольно выбранной пары шаров по крайней мере один синий. Сколько в комнате красных шаров? (6)
Подсказка
Подумайте, может ли в комнате быть два красных шара.
Решение:
Поскольку среди двух любых шаров один синий, то двух красных шаров в комнате быть не может. Значит, в комнате находятся 84 синих воздушных шара и 1 красный.
Ответ 1 шар.
Задача 35
Среди 4-х людей нет трех с одинаковым именем, одинаковым отчеством или одинаковой фамилией, но у любых двух людей совпадают либо имя, либо отчество, либо фамилия. Может ли так быть? .(6)
Подсказка
Попробуйте написать эти имена.
Решение:
Да, так может быть, например: Иван Иванович Иванов, Иван Петрович Петров, Петр Иванович Петров, Петр Петрович Иванов
Ответ: Иван Иванович Иванов, Иван Петрович Петров, Петр Иванович Петров, Петр Петрович Иванов
ЗАДАЧА 36 Сколько трёхзначных чисел можно составить из цифр 2,4,6,8, если цифры в записи числа не повторяются?
Решение: стр. 39 учебника, 4*3*2= 24 трехзначных числа
Задача 37: Сегодня Сереже исполнилось 10 лет, а Вове - 1 год. Каков будет возраст Сережи, когда он станет втрое старше Вовы?
Решение: Серёже-15, Вове 5 через 5 лет
Задача 38: Составьте из цифр 1, 2, 3, 4, 5, 6, 7, 8, 9 магический квадрат, то есть разместите их в таблице 3 × 3 так, чтобы суммы чисел по строкам, столбцам и двум диагоналям были одинаковы.
Решение:
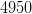
Задача 39: Девочка заменила каждую букву в своем имени ее номером в русском алфавите и получила число 2011533. Как ее зовут? Имеет ли задача однозначный ответ? Почему?
Задача 40: Школьники посадили вдоль дороги (по прямой) 25 деревьев. Расстояние между двумя любыми соседними деревьями одинаковое. Найдите это расстояние, если между крайними деревьями 600 дм.
. Тем более, что подобные задачи мы с детьми решаем на моем .
Решение: 600:24 = 25 дм - расстояние между двумя любыми соседними деревьями
ЗАДАЧА 41
Вася может получить число 100, используя десять двоек, скобки и знаки арифметических действий:
100 = (22 : 2 - 2 : 2) · (22 : 2 - 2 : 2)
Улучшите его результат: используйте меньшее число двоек и получите число 100.
В шестом классе вместо двоек были тройки, в седьмом - семерки. Но на решение задачи это никак не влияло.
Решение задачи
Один из вариантов, не самый короткий, предусматривает использование 8 двоек:
(22 - 2) : 2 · (22 - 2) : 2 = 100
Аналогично для троек и семерок:
(33 - 3) : 3 · (33 - 3) : 3 = 100
(77 - 7) : 7 · (77 - 7) : 7 = 100
На занятиях мои четвероклассники и даже третьеклассники нашли вариант из 6 двоек:
(222 - 22) : 2 = 100
Аналогично: (333 - 33) : 3 = 100, (777 - 77) : 7 = 100
ЗАДАЧА 42
разрежьте фигуру на 3 равные части.
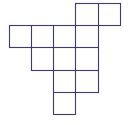
Задача № 43 . Составьте квадрат, используя ровно четыре из пяти изображенных ниже фигур. Каждую из четырех выбранных Вами фигур можно использовать только один раз.
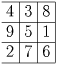
Задача 44 . Без ореха (от дупла до орешника) белка бежит со скоростью 4 м/сек, а с орехом (от орешника до дупла) - со скоростью 2 м/сек. На путь от дупла до орешника и обратно она тратит Шаг 1. Посчитаем, сколько клеточек содержится в фигуре. Их 12.
Шаг 2. Определим, сколько клеточек должна содержать каждая полученная в результате разрезания часть. 12:3 = 4.
Шаг 3. Нарисуем все возможные комбинации из 4 клеточек. Их я насчитал 5 (не рассматриваем фигуры, где клеточки соединяются только «углом»).

Шаг 4. Исследуем все варианты и отбрасываем те, что не подходят. В итоге получаем возможное решение:

ЗАДАЧА 45:
Как отмерить 8 л воды, находясь около реки и имея два ведра вместимостью 10 л и 6 л? (8 л воды должно получиться в одном ведре).
Решение задачи
Запишем последовательность действий в таблицу, указывая в первом столбце действие, а во втором и третьем - результат, т.е. сколько воды остается в каждом ведре после действия.
Действие
Ведро
10 л
Ведро
6 л
Изначально оба ведра пустые
0
0
Наполним большое ведро из речки
10
0
Перельем из большого в маленькое 6 л
4
6
Выльем всю воду из маленького
4
0
Перельем из большого в маленькое всю воду, т.е. 4 л
0
4
Наполним большое ведро из речки
10
4
Отольем из большого ведра столько, чтобы наполнить маленькое до краев, т.е. 2 л.
8
6
В результате в большом ведре останется ровно 8 литров.
ЗАДАЧА 46:
Белоснежка вошла в комнату, где вокруг круглого стола стояло 30 стульев. На некоторых из стульев сидели гномы. Оказалось, что Белоснежка не может сесть так, чтобы рядом с ней никто не сидел. Какое наименьшее число гномов могло быть за столом?
(Объясните, как должны были сидеть гномы и почему, если бы гномов было меньше, Белоснежка нашла бы стул, рядом с которым никто не сидит).
Решение задачи
Каждый гном может сделать недоступными для Белоснежки 3 стула - тот, на котором он сидит, а также стулья справа и слева. Поэтому наименьшее число гномов 30 : 3 = 10. Гномы могут сидеть, например, на стульях с номерами 3, 6, 9, … 30 - через каждые два стула на третьем. При таком расположении любой пустой стул оказывается рядом с занятым (либо справа, либо слева).
Докажем, что при меньшем числе гномов Белоснежка найдет свободный стул без соседей. Пусть гномов за столом 9. Назначим любого гнома старшим и начнем отсчет стульев с него - т.е «старший» гном сидит на стуле №1. При этом Белоснежка уже не сможет занять стулья №30 и №2. Следующий гном должен сесть не дальше, чем на стул № 4, иначе Белоснежка сядет на стул № 3 - и рядом с ней окажутся свободными оба соседних стула - №2 и №4. Рассуждая аналогично, приходим к выводу, что третий гном сядет на стул №7, четвертый - на стул №10 и т.д. Девятому гному достанется стул №25. А это означает, что в распоряжении Белоснежки будут стулья №27, 28 и 29, на любом из которых она сможет расположиться без соседей по бокам.
ЗАДАЧА 47:
Папа, Маша и Яша идут в школу. Пока папа делает 3 шага, Маша делает 5 шагов. Пока Маша делает 3 шага, Яша делает 5 шагов. Маша и Яша посчитали, что вместе они сделали 400 шагов. Сколько шагов сделал папа?
(Напишите решение задачи, а не только ответ).
Решение задачи
Рассмотрим отрезок пути, на котором Маша делает 3 шага, а Яша - 5 шагов. Вместе они делают на таком отрезке 8 шагов. Значит, они прошли 400 : 8 = 50 таких отрезков. И Маша сделала 50 · 3 = 150 шагов.
Теперь рассмотрим другой отрезок - на котором уже папа делает 3 шага, а Маша - 5 шагов. Таких отрезков было 150 : 5 = 30. Отсюда легко вычислить, сколько шагов сделал папа: 30 · 3 = 90 шагов.
Ответ: папа сделал 90 шагов
задача 48: 1. На ступеньках дома сидят рядышком мальчик и девочка.
- Я мальчик, - говорит ребёнок с чёрными волосами.
- А я девочка, - говорит ребёнок с рыжими волосами.
Если по крайней мере один из детей говорит неправду, то кто из них мальчик, а кто девочка?
Решение
Для двух произвольных высказываний существуют четыре возможные комбинации типа «истина - ложь», а именно:
И - И, И - Л, Л - И, Л - Л.
Первая из них исключается, поскольку в условии оговаривается, что по крайней мере одно из высказываний является ложным. Вторая и третья комбинации также исключается, потому что если один ребёнок врал, то и другой не мог говорить правду, иначе мы бы имели дело с двумя мальчиками или с двумя девочками, что противоречит условию. Следовательно, оба говорили неправду.
Итак, у мальчика рыжие волосы, а у девочки чёрные.
Задача 49:
Можно ли расставить по окружности 20 красных и несколько синих фишек так, чтобы в каждой точке, диаметрально противоположной красной фишке, стояла синяя и никакие две синие фишки не стояли рядом?
Решение
Из условия следует, что красные и синие фишки должны чередоваться (на окружности), значит, всего их 40. Фишки по окружности размещаются равномерно в том смысле, что две диаметрально противоположные фишки делят множество оставшихся 38 фишек на две части по 19 фишек, расположенные в одной и другой полуокружностях относительно двух данных фишек. Это так, потому что согласно условию, каждая фишка имеет диаметрально противоположную. Диаметрально противоположные фишки имеют разный цвет, поэтому 19 фишек, расположенные в одной из полуокружностей должны чередоваться по цвету и начинаться и заканчиваться фишками разного цвета, что невозможно при нечётном 19. Следовательно, указанная в задаче расстановка фишек не возможна.
Ответ: нельзя.
Задача 50:
Разбирается дело Брауна, Джонса и Смита. Один из них совершил преступление. В процессе расследования каждый из них сделал по два заявления.
Браун: «Я не делал этого. Джонс не делал этого.»
Джонс: «Браун не делал этого. Смит сделал это.»
Смит: «Я не делал этого. Браун сделал это.»
Было установлено далее, что один из них дважды солгал, другой дважды сказал правду, третий - раз солгал, раз сказал правду. Кто совершил преступление?
Решение
Если вор - Смит, то и Браун, и Джонс оба сказали правду. Если вор - Джонс, то и Браун, и Смит одновременно сказали и правду, и ложь. Итак, Браун - преступник. Джонс оба раза солгал, Смит оба раза сказал правду, Браун один раз солгал, второй раз сказал правду.
Задача 51:
Шурик, Трус, Балбес и Бывалый участвовали в турнире по домино и заняли первые четыре места. Сумма мест, занятых Шуриком, Трусом и Балбесом, равна 6, сумма мест Труса и Бывалого тоже равна 6. Какое место занял каждый из них, если Трус занял более высокое место, чем Шурик? Объясните, как вы получили ответ.
Решение.
Ответ: 1. Балбес; 2. Трус; 3. Шурик; 4. Бывалый. Из первого условия следует, что Шурик, Трус и Балбес заняли первые три места в каком-то порядке, а из второго, - что Трус и Бывалый заняли второе и четвертое места. Значит, Трус - второй, Бывалый - четвертый. Из последнего условия следует, что Балбес - первый, а Шурик - третий.
Задача 52.
В бочке находится не менее 13 литров молока. Как отлить из нее 8 литров молока с помощью пустых пятилитрового и девятилитрового ведер?
Решение.
Наполняем из бочки девятилитровое ведро и отливаем из него 5 л в пятилитровое. Эти 5 л выливаем обратно в бочку, а в пятилитровое ведро выливаем оставшиеся 4 л из девятилитрового. Далее снова наполняем девятилитровое ведро из бочки и отливаем 1 л в пятилитровое. Теперь в девятилитровом ведре находится 8 литров молока.
Задача 53.
Количество цифр, потребовавшихся для нумерации всех страниц энциклопедического словаря, не превосходит 2009 (первая страница имеет номер 1). Если бы в словаре было на одну страницу больше, то это количество превысило бы 2009. Сколько страниц в словаре? Объясните, как вы получили ответ.
Решение. На однозначные номера потрачено 9 цифр, на двузначные - 90×2 = 180 цифр. Поэтому на трехзначные номера остается не более 2009 - 9 - 90×2 = 1820 цифр. Так как 1820 : 3 = 606 (ост. 2), то страниц с трехзначными номерами в словаре 606, а всего страниц - 9 + 90 + 606 = 705.
Ответ: 705 страниц.
Задача 54.
Коля заплатил 115 руб за четыре тетради, два карандаша и резинку, Саша - 140 руб за две тетради, семь карандашей и две резинки. Сколько заплатил Антон за две тетради, три карандаша и резинку? Объясните, как вы получили ответ.
Решение.
Так как покупки Коли и Саши вместе составляют утроенную покупку Антона, то Антон потратил (115 + 140) : 3 = 85 руб.
Ответ: 85 руб.
Задача 55.
Сколько раз к наибольшему однозначному числу надо прибавить наибольшее двузначное число, чтобы получить наибольшее трёхзначное.
Решение.
9 + 99п = 999
99п = 990
п = 10
Значит нужно прибавить 10 раз.
Ответ: 10 раз
Задача № 56 : В примере на сложение двух чисел первое слагаемое меньше суммы на 2000, а сумма больше второго слагаемого на 6. Восстановите пример.
. Ответ: 6+2000 = 2006. Если из суммы двух чисел вычесть одно из слагаемых, то получится другое слагаемое. Из условия следует, что второе слагаемое равно 2000, а первое - равно 6.
Задача № 57 :В день рождения дяди Федора почтальон Печкин хочет выяснить, сколько тому лет. Шарик говорит, что дяде Федору больше 11 лет, а кот Матроскин утверждает, что больше 10 лет. Сколько лет дяде Федору, если известно, что ровно один из них ошибся? Ответ обоснуйте.
Ответ : Федору 11 лет. Заметим, что если не ошибся Шарик, то не ошибся и Матроскин, что противоречит условию. Значит, Шарик сказал неправду, в отличие от кота Матроскина. Таким образом, дяде Федору больше 10 лет, но не меньше 11. Следовательно, дяде Федору исполнилось 11 лет.
Задача № 58 :. В забеге от Воробьевых гор до Красной площади приняли участие три спортсмена. Сначала стартовал Гриша, затем - Саша, и последней - Лена. После финиша выяснилось, что во время забега Гриша обгонял других 10 раз, Лена - 6 раз, Саша - 4 раза, причем все трое ни разу не оказывались в одной точке одновременно. В каком порядке финишировали спортсмены, если известно, что они пришли к финишу в разное время? Ответ обоснуйте.
. Ответ: первым финишировал Гриша, затем - Саша, и последней - Лена.
Гриша стартовал первым. Чтобы он смог совершить 10 обгонов, необходимо чтобы Саша и Лена обогнали его хотя бы 10 раз. Так как общее количество обгонов Саши и Лены равно 6 + 4 = 10, то они обгоняли только Гришу и не обгоняли друг друга. После того, как Гриша совершил все 10 обгонов, он опять оказался первым. Значит, спортсмены финишировали в том же порядке, в котором и стартовали.
Гриша стартовал первым. Чтобы он смог совершить 10 обгонов, необходимо чтобы Саша и Лена обогнали его хотя бы 10 раз. Так как общее количество обгонов Саши и Лены равно 6 + 4 = 10, то они обгоняли только Гришу и не обгоняли друг друга. После того, как Гриша совершил все 10 обгонов, он опять оказался первым. Значит, спортсмены финишировали в том же порядке, в котором и стартовали.
Школьный этап олимпиады по математике в 5-6-х классах
Задача №1. Вычеркните в числе 4000538 пять цифр так, чтобы оставшееся число стало наибольшим.
Задача №2. В записи трёхзначного числа единиц в два раза меньше, чем десятков, а сотен в два раза больше, чем десятков. Найти это число, если в нём четыре десятка.
Задача №3. Расшифруйте два ребуса, в которых одинаковым буквам соответствуют одинаковые цифры, а разным буквам - разные цифры в обоих примерах.
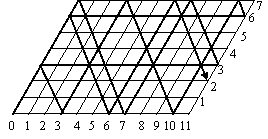
Задача №4. Имеется двое песочных часов: на 3 минуты и 7 минут. Яйцо варится 11 минут. Как отмерить это время при помощи имеющихся часов.
Задача №5. Трое учеников пошли на рыбалку, взяв с собой лодку, выдерживающую нагрузку до 100 кг. Как перебраться ученикам с берега реки на остров, если их массы равны 40 кг, 50 кг, 70 кг?
Ответы 5-6-й классы
Ответ к задаче №1: 58.
Ответ к задаче №2: 842.
Ответ к задаче №3: А=3; Б=2; В=1; Г=5.
Ответ к задаче №4: Перевернуть обои часы, когда пройдёт три минуты, в семиминутных часах останется 4 минуты. Поставить яйцо в данный момент вариться, когда 4 минуты закончатся, перевернуть семиминутные часы обратно. Получим: 4+7=11.
Ответ к задаче № 5: План действий:
-
сначала переправляются два лёгких;
-
один из них перегоняет лодку обратно;
-
самый тяжёлый садится в лодку и переплывает один;
-
второй лёгкий садится в лодку и перегоняет её обратно;
-
двое лёгких садятся в лодку и переправляются на остров.
№ 1: На прямой взяли 4 точки. Сколько всего получилось отрезков, концами которых являются эти точки? (2 балла)
Ответ: Всего получилось 6 отрезков.
№ 2: Винни-Пуху подарили в день рождения бочонок с мёдом массой 7кг. Когда Винни-Пух сьел половину мёда, то бочонок с оставшимся мёдом стал иметь массу 4кг. Сколько килограммов мёда было первоначально в бочонке? (3 балла)
Ответ: В бочонке первоначально было 6кг мёда.
Решение: Оставшаяся половина мёда в бочонке имеет массу
7-4=3(кг). Значит, всего мёда 3*2=6(кг).
№ 3 : Сумма трех чисел равна их произведению. Эти числа различные и однозначные. Найти эти числа. (3 балла)
Ответ: 1,2,3.
Решение: 1+2+3=1*2*3
№ 4 : Турист поднимался в гору 5 часов, проходя каждый час 3 км. На обратном пути он увеличил скорость на 2 км/ч. Сколько часов потребовалось туристу на обратный путь? (3 балла)
Ответ: Туристу на обратный путь понадобилось 3 часа.
Решение: 5*3=15(км) - весь путь
3+2=5(км/ч) - скорость на обратном пути
15:5=3(ч) - время, потраченное на обратный путь
№ 5: С хозяйством попа справляются 10работников. Каждый работник в день съедает каравай хлеба и другие продукты. Поп принял на работу Балду.
Живет Балда в поповом доме,
Спит себе на соломе,
Ест за четверых,
Работает за семерых.
Поп прогнал лишних работников. Сколько караваев хлеба экономил поп ежедневно? (2 балла)
Ответ: Поп ежедневно экономил три каравая.
Решение: Балда работал за семерых, а ел за четверых. Экономия составляет
7- 4=3(каравая)
№ 6: По дереву ползет гусеница. За день она поднимается на 6 метров, а ночью опускается на 4 метра. За сколько дней она доползет до вершины, если высота дерева 14 метров?
Ответ: За 5 дней
Решение: В последний день гусеница поднимется на 6 метров, значит ей надо проползти ещё 14-6=8(м). В день она поднимается на 6-4=2(м). Тогда 8 метров проползет за 8:2=4 (дня). Все время движения составит 1+4=5 (дней)
Требуется распилить бревно на 6 частей. Каждый распил занимает 2 минуты. Сколько времени потребуется на эту работу?
Ответ: 10 минут
Решение: Распилов будет 5. Затраченное время 5*2=10 (мин)