Конспект урока «График и свойства функции y=ax2», 9 класс

Урок математики в 9 классе по теме

«График и свойства функции y=ax²»

Учитель: Сиканкина А.И.

Цели:

1. Закрепить: знания свойств квадратичной функции и общих свойств функций; умения строить график квадратичной функции по точкам и изображать график схематически для а>0, а<0.

2. Развивать познавательный интерес учащихся, навыки сравнения и анализа; развивать монологическую речь в ходе объяснений, обоснований выполняемых действий; коммуникативные навыки; навыки самостоятельной работы; умение работать с бланком ответов при решении тестов.

3. Воспитывать любовь к предмету.

Тип урока: комбинированный урок по теме «График и свойства функции

y=ax² ».

Средства обучения: мультимедийная доска; презентация; листы самоконтроля.

Ход урока.

1. Организационный момент

2. Постановка целей урока

3. Проверка домашнего задания

4. Актуализация

   1. Какая кривая является графиком функции y=ax²? (парабола)

   2. Как зависит направление ветвей параболы от коэффициента а?

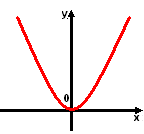
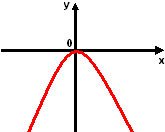
y=ax², а >0 y=ax², а < 0.

3. Какая точка является вершиной параболы y=ax²? (0;0)

4. Что является осью симметрии графика функции y=ax²?

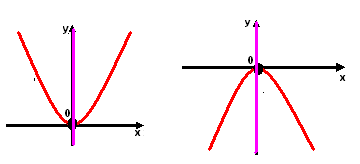
Ось Оy

5. Сформулируйте определение графика функции y=ax²

Графиком функции y=ax² является парабола с вершиной в начале координат; ее ось симметрии служит ось у; при а>0 ветви параболы направлены вверх, при а<0 ветви направлены вниз.

6. Как влияет величина а на «крутизну» параболы?
   При а>0.
   Чем больше коэффициент а, тем больше «крутизна» параболы

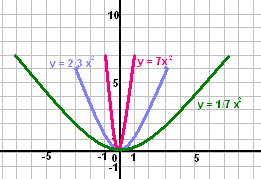
При а<0.
Чем меньше коэффициент а, тем больше «крутизна» параболы

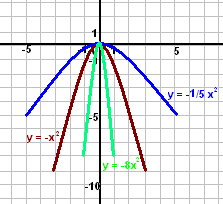
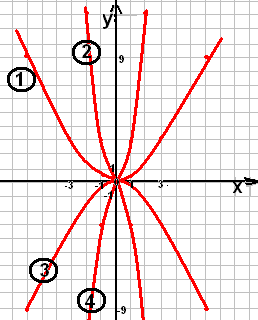
Пример №1

y = -1/3 x² ?
y = 1/3 x² ?
y = -3x² ?
Y = 3x² ?

Самостоятельная работа. Задание №1

Найдите правильный ответ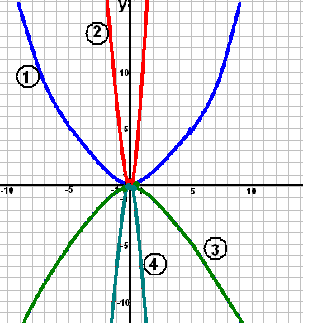

а) 1 - y=5x² ; 2 - y= -5x² ;
3 - y= 1/5 x² ; 4 - y=-1/5 x²
б) 1 - y=-1/5 x² ; 2 - y= -5x² ;
3 - y= 1/5 x² ; 4 - y=5x²
в) 1 - y= 1/5 x² ; 2 - y=5x² ;
3 - y=-1/5 x² ; 4 - y= -5x²
г) 1 - y=5x² ; 2 - y= 1/5 x² ;
3 - y= -5x²; 4 - y=-1/5 x²

Функция y=ax²

а>0 а<0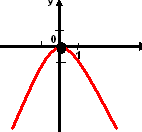

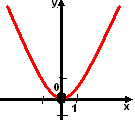
возрастает на [0;+∞) возрастает на (-∞;0]

убывает на (-∞;0] убывает на [0;+∞)

Самостоятельная работа. Задание №2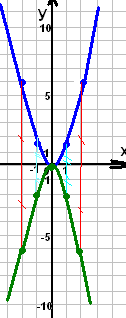

Функция y = -3,6 x² возрастает на промежутке

а) [0;+∞) б) (-∞;0) в) (0;+∞) г) (-∞;0]

Пример №2

Дан график функции y=1,5 x², постройте график функции y=-1,5 x²

Самостоятельная работа. Задание №3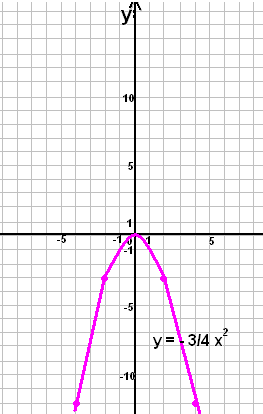

Дан график функции y = -3/4 x², постройте график

функции y = 3/4 x²

Пример №3
Принадлежит ли точка ( -2;-12) графику функции y=-3 x²

Самостоятельная работа. Задание №4

Какая из точек принадлежит графику функции y = -4 x2 ?

а) (1/2; -1) б) (3; -1/2) в) (1;4) г) (-2;8)

Пример №4

Пересечет ли прямая у=4 график функции
а) у= ¼ x²б) у= - ¼ x² Если да, то в каких точках.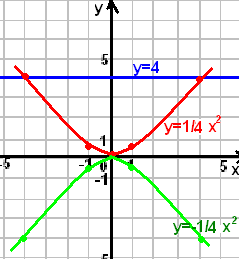

а) у= ¼ х²

¼ х² = 4

х² =16

(-4;4) и (4;4)

б) у= - ¼ х²

-¼ х² = 4

х² =-16

нет корней.

Самостоятельная работа. Задание №5

Какая из прямых не пересечет график функции y = 14 x² ?

а) у = 1 б) у = 90 в) у = -5 г) у = 0

5. Закрепление изученного материала

№ 201 (а,в) , № 202 (б)

6. Подведение итога урока

Заполнение листов самоконтроля и выставление оценок.

7. Домашнее задание

№ 201 (б,г) , № 202 (а,в)

Самостоятельная работа

1. Найдите правильный ответ

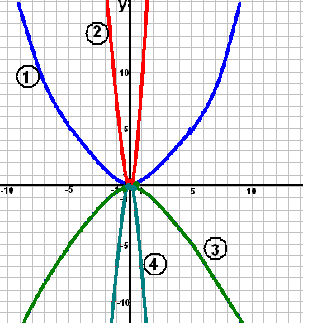
а) 1 - y=5x² ; 2 - y= -5x² ;
3 - y= 1/5 x² ; 4 - y=-1/5 x²
б) 1 - y=-1/5 x² ; 2 - y= -5x² ;
3 - y= 1/5 x² ; 4 - y=5x²
в) 1 - y= 1/5 x² ; 2 - y=5x² ;
3 - y=-1/5 x² ; 4 - y= -5x²
г) 1 - y=5x² ; 2 - y= 1/5 x² ;
3 - y= -5x²; 4 - y=-1/5 x²

2. Функция y = -3,6 x² возрастает на промежутке

а) [0;+∞) б) (-∞;0) в) (0;+∞) г) (-∞;0]

3. Дан график функции y = -3/4 x² , постройте график функции y = 3/4 x² .

4. Какая из точек принадлежит графику функции y = -4 x²?

а) (1/2; -1) б) (3; -1/2) в) (1;4) г) (-2;8)

5. Какая из прямых не пересечет график функции y = 14 x² ?

а) у = 1 б) у = 90 в) у = -5 г) у = 0

Лист самоконтроля

ученика 9 класса МКОУ Чебаклинская СОШ

________________________________.

Урок математики по теме «График и свойства функции y=ax²»

1 балл

2 балла

3 балла

Актуализация знаний

Устная работа

Самостоятельная работа

Задание 1

Задание 2

Задание 3

Задание 4

Задание 5

Решение заданий

№ 201 (а,в) и № 202 (б)

Всего баллов ________________

«5» - 9-11 баллов

«4» - 6-8 баллов

«3» - 4-5 баллов

Оценка за урок______________

Литература:

1. Математика 9 класс. Дорофеев В.Г. 2007г