Разработка урока по алгебре в 8 классе Способы решения квадратных уравнений

Урок по алгебре в 8 классе по теме:

« Десять способов решения квадратных уравнений ».

Цели урока: повторить известные способы решения квадратных уравнений, разобрать новые способы и уметь применять их на практике.

Оборудование: компьютер, проектор, экран.

Ход урока.

I.Орг. момент.

Сообщение темы урока, целей урока. (слайд1)

II. Повторение пройденного материала. ( слайд 2)

1. Дайте определение квадратного уравнения.

2. Виды квадратных уравнений.

3. Теорема Виета.

III. Рассмотрим способы решения квадратных уравнений. (слайд3,4)

Определить вид квадратного уравнения и назвать способ его решения:

1. х² + 2х = 0

2. х² - 81 = 0

1 способ: разложение левой части уравнения на множители.

Слайд 5.

Определить вид квадратного уравнения и назвать способ его решения:

х² + 6х - 7 = 0

2 способ: метод выделения полного квадрата

3 способ: по формулам

4 способ: с использованием теоремы Виета (прямой и обратной)

IV. Изучение нового материала

Слайд 6.

5 способ: «переброска» коэффициентов.

Объяснение материала.

Рассмотрим квадратное уравнение ах² + вх + с =0, где коэффициент а не равен 0. Умножим обе части уравнения на коэффициент а, получаем уравнение а²х² + авх + ас = 0. Пусть ах = у, откуда х = у/а; тогда приходим к уравнению у² +ву +ас = 0, равносильному данному. Его корни найдем с помощью теоремы Виета. Окончательно получаем х_{1 =} у₁/а, х₂ = у₂/а. При этом способе коэффициент а умножается на свободный член, как бы «перебрасывается» к нему, поэтому способ и называют способом «переброски». Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета, и когда дискриминант есть точный квадрат.

Слайд 7

Решить уравнение: 2х² -11х + 15 = 0.

Решение:

1. Коэффициент а=2 умножим на свободный член с=15 («перебросим» коэффициент). Получим уравнение: у² - 11у + 30 = 0, где х = у/а, т.е х = у/2

2. По теореме Виета получаем: у₁=5, у₂=6.

3. х₁=5/2=2,5 х₂=6/2=3.

Ответ. х₁ =2,5; х₂ = 3.

Закрепление материала.

Самостоятельно решить уравнение:

I вариант: 4х² + 12х + 5 = 0 ( у² +12у + 20=0, х = у/4 )

IIвариант: 6х² + 5х - 6 = 0 ( у² + 5х - 36=0, х = у/6 )

Ответ. 1 вариант. х₁= -0,5 ; х₂= -2,5.

2 вариант. х₁= 2/3 ; х₂= -1,5.

Слайд 8.

6 способ: Свойства коэффициентов квадратного уравнения.

Объяснение материала.

Теорема:

если сумма коэффициентов квадратного уравнения

ах² + вх + с = 0 равна нулю (т.е. а+в+с=0), то

х₁ =1,

х₂ =с/а.

Слайд 9

Решить уравнение: 11х² + 25х - 36 = 0.

Решение:

Применим теорему о коэффициентах квадратного уравнения:

11+25+(-36)=0, значит х₁ =1, х₂ =-36/11.

Ответ. х₁ =1, х₂ =-36/11.

Устно решить уравнения:

а) 5х² -7х+2=0

б) 3х² +5х-8=0

Ответ. а) х₁ =1, х₂ =2/5

б) х₁ =1; х₂ = -8/3

Слайд 10

7 способ: Решение квадратных уравнений с помощью номограммы.( для приведенных квадратных уравнений)

Объяснение нового материала.

Это старый и незаслуженно забытый способ решения квадратных уравнений с помощью четырехзначных математических таблиц В.М. Брадиса

( таблица XXII, способ описан на стр.83).

Номограмма для решения уравнения z²+pz+q=0. Эта номограмма позволяет, не решая квадратного уравнения, по его коэффициентам определить корни уравнения.

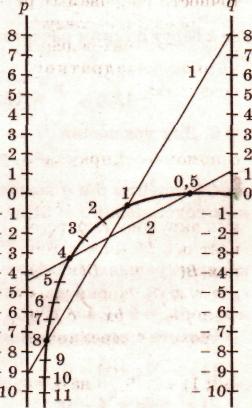
Слайд 11.

Примеры.

1. Для уравнения

z² - 9z + 8 = 0

номограмма дает корни

z₁ = 8,0 и z₂ = 1,0

( см рис. ).

2. Решим с помощью

номограммы уравнение

2z² -9z + 2 = 0.

Разделим коэффициенты этого уравнения на 2, получим уравнение

z² -4,5z+1 = 0.

Номограмма дает корни z₁ = 4 и z₂ =0,5.

С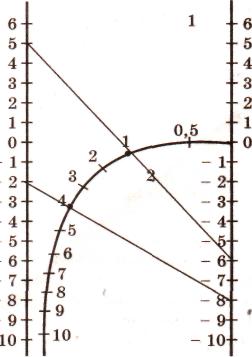лайд 12.

Для уравнения

z² + 5z - 6 = 0

номограмма дает положительный корень z₁ = 1,0, а отрицательный корень находим, вычитая положительный корень из - р, т. е.

z₂ = - р - 1 = = - 5 - 1 = - 6,0 .

С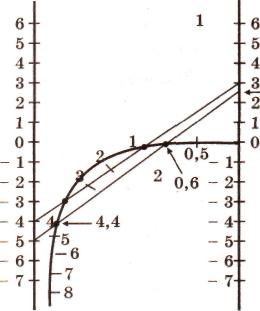лайд 13.

Для уравнения

Z² + 4z + 3 = 0,

оба корня которого отрицательные числа, берем z₁ = - t₁, z₂= - t₂ и находим по номограмме два положительных корня t₁ и t₂

уравнения t₂ - 4t + 3 = 0,

это t₁ = 1 и t₂ = 3,

а затем z₁ = - t₁ = - 1 и

z₂ = - t₂ = - 3.

Если коэффициенты р и q выходят за пределы шкалы, то выполняют подстановку

z = kt и решают с помощью номограммы уравнение

t² +(p/k)k+ q/k² =0,

где k берут с таким расчетом, чтобы имели место неравенства

-12,6 < p/k < 12,6,

- 12,6 < q/k2 < 12,6.

Слайд 14

Решите с помощью номограммы уравнения:

I вариант

1. z² - 4z + 4 = 0

2. z² -z - 6 = 0

3. z² + 5z + 4 = 0

Ответ. a) z₁ =3,5; z₂ =1,0

b) z₁ =3; z₂ = -2

c) z₁ = -4; z₂ = -1.

II вариант

1. z² - 7z + 6 = 0

2. z² + 4z - 5 = 0

3. z² + 5z + 6 = 0

Ответ. a) z₁ =6,5; z₂ =1,5

b) z₁ =1; z₂ = -5

c) z₁ = -3; z₂ = -2.

Слайд 15.

8 способ: Графическое решение квадратного уравнения.

Объяснение материала.

Если в уравнении

х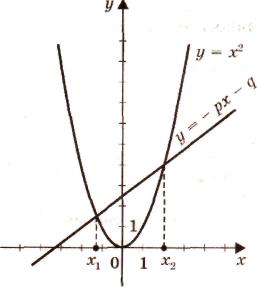² + рх + q = 0

перенести второй и третий члены в правую часть, то получим

х² = - рх - q.

Построим графики зависимостей

у = х² и у= -рх- q

График первой зависимости - называется парабола. Она проходит через начало координат.

График второй зависимости - прямая.

Возможны следующие случаи:

1. прямая и парабола
   
   могут пересекаться в двух
   
   точках, абсциссы точек пе­-
   
   ресечения являются кор­-
   
   нями квадратного уравне­-
   
   ния ( см рис. ).

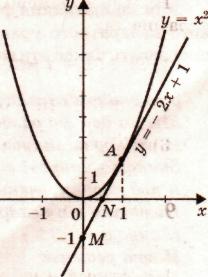
2. прямая и парабола могут касаться (только одна общая точка), т. е. уравнение имеет одно решение.

3. прямая и парабола не
   
   имеют общих точек, т. е.
   
   квадратное уравнение не имеет корней.

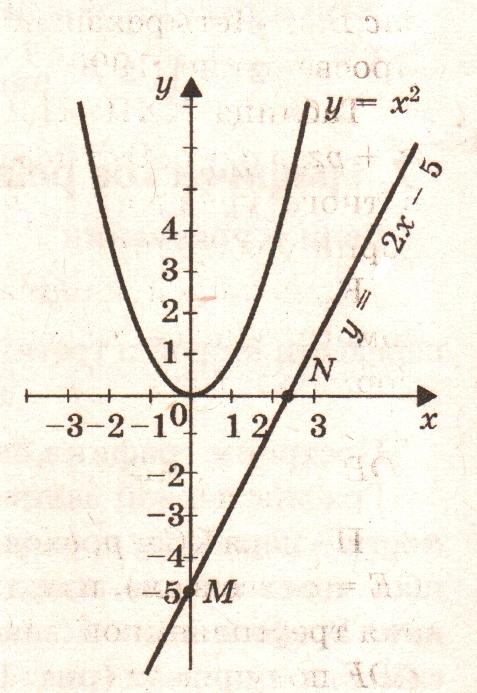
Слайд 16.Определить по рисунку, сколько корней имеет квадратное уравнение (обосновать):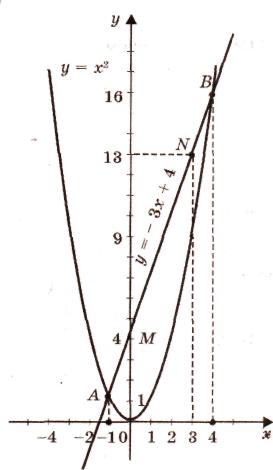

х² - 3х - 4 = 0.

Назовите корни этого уравнения.

Ответ. 2 корня: х = 4; х = -1.

Слайд 17.

Определить, сколько корней имеет квадратное уравнение (обосновать):

х² - 2х + 1 = 0.

Назовите корни этого уравнения.

Ответ. 1 корень: х=1.

Слайд 18.

Определить, сколько корней имеет квадратное уравнение (обосновать):

х² - 2х + 5 = 0.

Назовите корни этого уравнения.

Ответ. Нет корней

Слайд 19.

9 способ: Решение квадратных уравнений с помощью циркуля и линейки.

Объяснение материала.

Графический способ решения квадратных уравнений с помощью параболы неудобен. Если строить параболу по точкам, то требуется много времени, и при этом степень точности получаемых результатов невелика.

Рассмотрим способ нахождения корней квадратного уравнения

ах² + bх + с = 0 c помощью циркуля и линейки.

С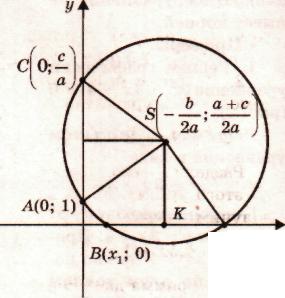лайд 20.

Схема построения:

1) Построим центр окружности S( -b 2a;а+с2а)

и А(0; 1);

2) проведем окружность с радиусом SA;

3) абсциссы точек пересечения этой окружности с осью Ох являются корнями исходного квадратного уравнения.

Слайд 21.

При этом возможны 3 случая:

1) Радиус окружности больше ординаты центра:

о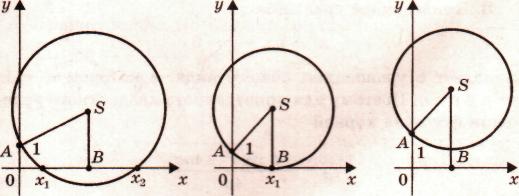кружность пересекает ось Ох в двух точках, т.е. уравнение имеет 2 различных корня.

2) Радиус окружности равен ординате центра

окружность касается оси Ох, т.е. уравнение имеет 2 равных корня

3) Радиус окружности меньше ординаты центра

окружность не имеет общих точек с осью Ох, т.е. уравнение не имеет корней.

С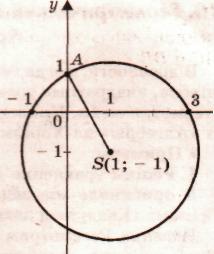лайд 22.

Назовите корни уравнения 1) х² - 2х - 3 = 0

по предложенному рисунку:

Слайд 23.

Н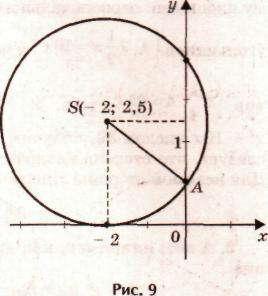азовите корни уравнения 2) х² + 4х + 4 = 0 по предложенному рисунку:

Слайд 24.

Н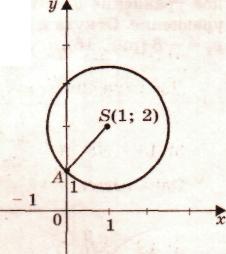азовите корни уравнения 3) х² - 2х + 3 = 0 по предложенному рисунку.

Слайд 25.

10 способ: Геометрический способ решения квадратных уравнений

Объяснение материала.

В древности, когда геометрия была более развита, чем алгебра, квадратные уравнения решали не алгебраически, а геометрически. Приведем ставший знаменитым пример из «Алгебры» ал-Хорезми.

Примеры.

1. Решим уравнение х² + 10х = 39.

В оригинале эта задача формулируется следующим

образом:

«Квадрат и десять корней равны 39» (рис.).

Решение.

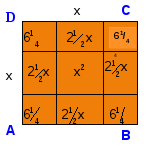
Рассмотрим квадрат со стороной х, на его сторонах

строятся прямоугольники так, что другая сторона каждого

из них равна 2¹ /₂, следовательно, площадь каждого

равна 2¹ / ₂ х. Полученную фигуру дополняют затем до

нового квадрата ABCD, достраивая в углах четыре равных

квадрата, сторона каждого из них 2¹ / ₂ , а площадь 6¹ /₄ .

Слайд 26.

Площадь S квадрата ABCD можно представить как сумму площадей: первоначального квадрата х², четырех прямоугольников (4*2¹/ ₂х=10х)

и четырех пристроенных квадратов (6¹/₄*4=25), т.е. S= х² + 10х + 25.

Заменяя х² + 10 числом 39, получим, что

S = 39 + 25 = 64, откуда следует, что сторона квадрата ABCD, т. е. отрезок АВ = 8. Для искомой стороны х первоначального квадрата получим

Х = 8 - 2¹/₂ - 2¹/₂ = 3.

V. Рефлексия.

Перечислите способы решения квадратных уравнений.

VI. Домашнее задание.

Решить с помощью циркуля и линейки квадратные уравнения:

1) х² - 2х - 3 = 0

2) х² + 4х + 4 = 0

3) х² - 2х + 3 = 0

4) х² - 5х + 4 = 0

VII. Подведение итогов. Выставление оценок.

Всем большое спасибо за урок!