Урок математики «Решение алгебраических уравнений». 10 класс

Лодыгин Владимир Дмитриевич,

заместитель директора по УР, учитель

математики высшей квалификационной

категории МБОУ «СОШ №5»

г.Северодвинска.

Конспект урока.

Класс: 10 (профильный)

Предмет: алгебра и математический анализ.

Тип урока: урок закрепления знаний.

Вид: урок - практикум.

Тема: «Решение алгебраических уравнений».

Цель.

1)закрепить знания видов, основных способов и приемов решения алгебраических уравнений;

продолжить формирование умений и навыков их решения;

2)способствовать развитию научного мышления учащихся (формирование умений анализировать условие задачи, актуализировать знания, сравнивать, сопоставлять данные, обобщать, планировать ход решения, делать выводы);

3)воспитывать настойчивость в достижении цели, волю.

Оборудование.

1.Таблицы:

«Схема Горнера», «Теорема Безу», «Условие равенства многочленов»,

Высказывание Д.Пойа: «Если вы хотите научиться плавать, то смело входите в воду, если хотите научиться решать задачи, то решайте их!».

2.Мультимедиапроектор.

3.Дидактические карточки- задания, материалы ЕГЭ.

План

I Организационный момент.

Вступительное слово учителя.

На предыдущих уроках вы познакомились с понятием алгебраического уравнения, видами алгебраических уравнений, изучили основные способы их решения. Сегодня продолжим работу по теме: «Решение алгебраических уравнений».

Ваша задача на уроке:

уточнить знания, приобрести опыт, то есть научиться по виду алгебраического уравнения определять способ его решения, а также учиться применять свои знания в нестандартной ситуации.

Задача на перспективу: подготовиться к решению нестандартных задач.

Эпиграфом к нашему уроку пусть послужат известные слова американского математика и методиста Д. Пойа: «Если вы хотите научиться плавать, то смело входите в воду, если хотите научиться решать задачи, то решайте их».

II. Обозначение проблемы.

Вашему вниманию предлагается задача:

Задача №1

Найдите наибольшее значение параметра а, при котором уравнение а x +b=0 с целыми коэффициентами имеет три различных корня, один из которых равен -2.

(задача из материалов ЕГЭ)

Прошу высказаться по поводу решения. Какие возникают вопросы.

Учащиеся:

- подставить -2 в уравнение.

Учитель: вы знаете, чтобы решить любую задачу, надо внимательно изучить её условие, (при этом ничего нельзя пропустить), проанализировать, что известно, что надо найти, какие знания ещё потребуются. Выстроить цепочку рассуждений, которая приведет к ответу. Всякий раз сопоставлять достигнутое на данном этапе с требуемым результатом.

Проанализируем условие нашей задачи.

Вопросы к обучающимся:

- к какому виду относится данное уравнение (целое алгебраическое);

- назовите коэффициенты многочлена (1; 5; а; в);

- каким требованиям должно удовлетворять значение параметра а (наибольшее целое число);

- каким требованиям ещё должно удовлетворять значение параметра а ; (при этом значении параметра а уравнение должно иметь три различных корня);

- как обеспечить наличие именно трех различных корней;

- какова роль параметра в;

- вспомните, если один корень многочлена известен, то какие операции с многочленом (преобразования его) можно выполнить.

Таким образом, вопросов много.

Ответы на поставленные вопросы, возможно, придут в ходе необходимого повторения, решения алгебраических уравнений известных видов.

III. Актуализация знаний

1.Проверка домашнего задания (показ видеофайла).

Дома решали уравнение:

.

Решение (комментируют обучающиеся)

Пусть tgz=x, z ≠ 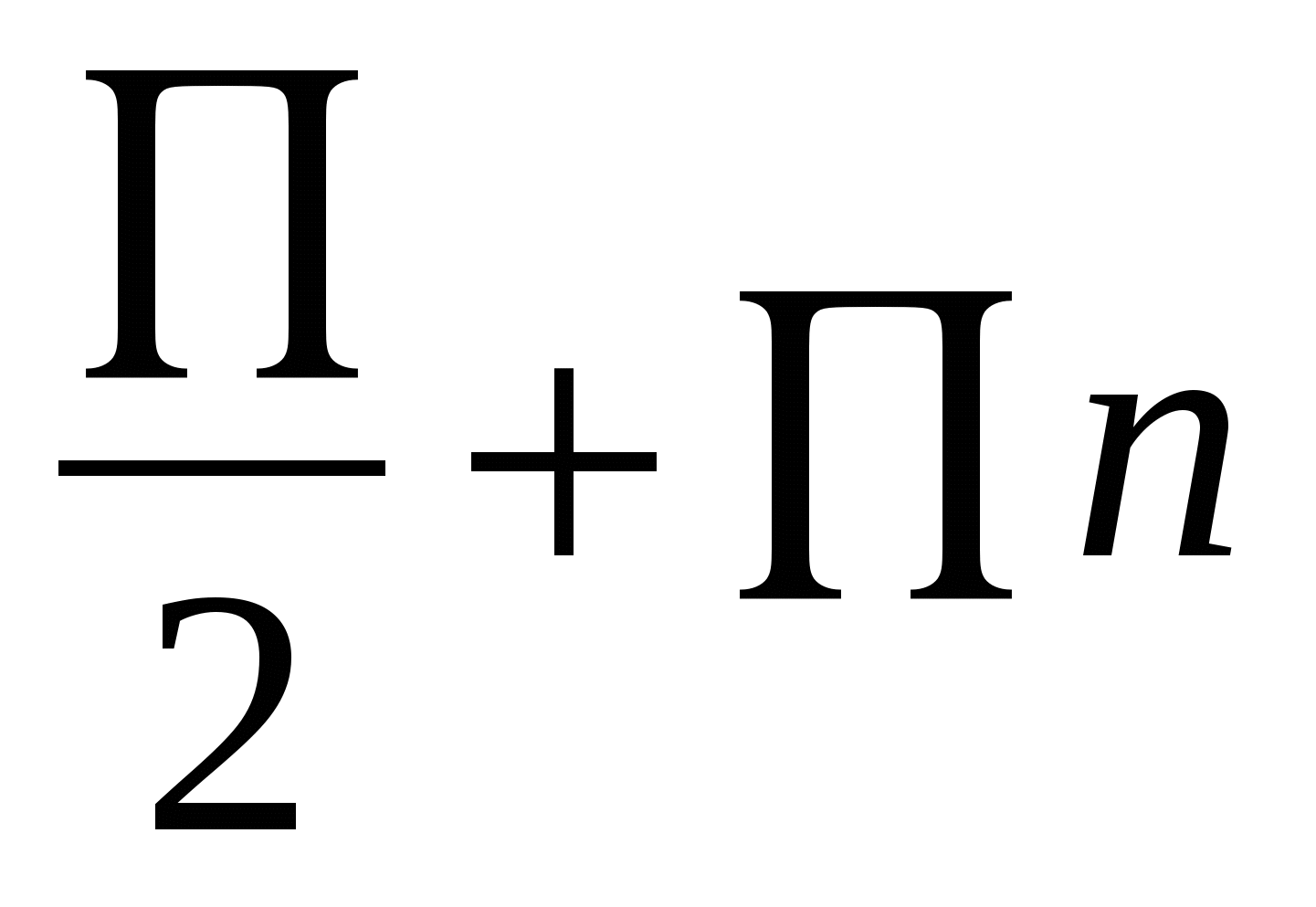, n Z,

получим уравнение - симметрическое.

Х=0 не является корнем (убеждаемся проверкой), делим на , получим равносильное уравнение:

.

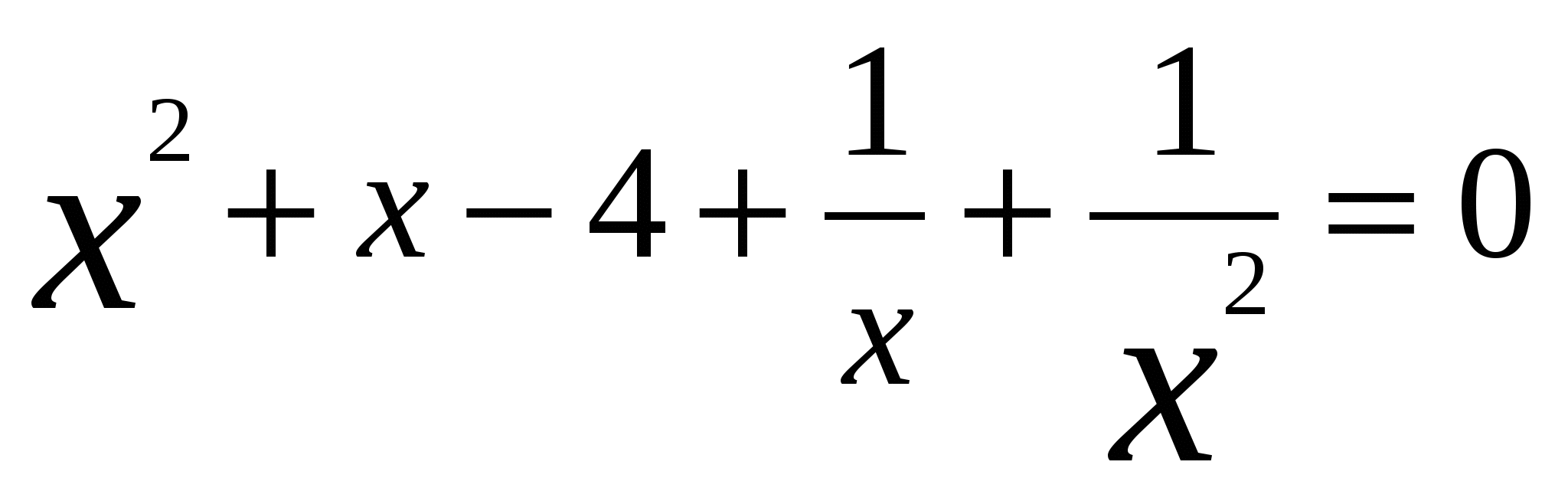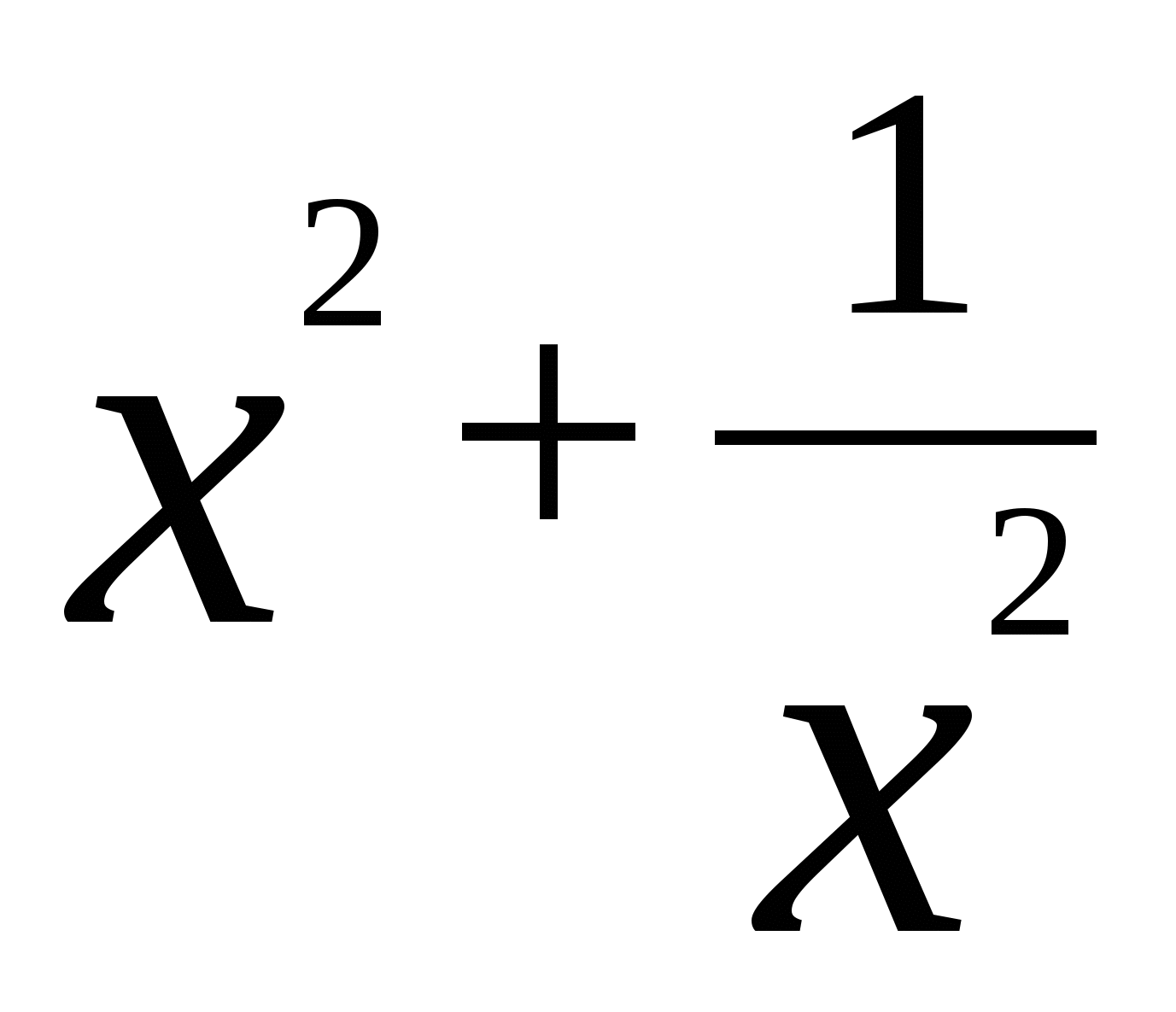()+(x+)-4=0. Новая переменная t = x+, тогда .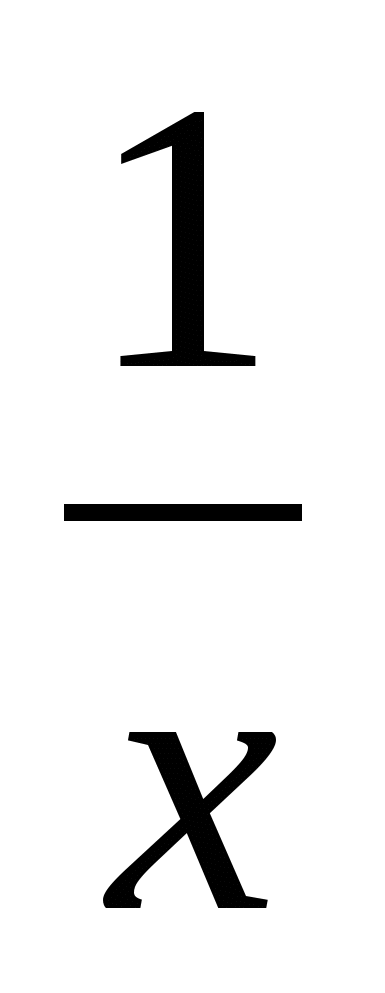

Уравнение с переменной t будет иметь вид:

, , .

Значит,

1) x+=-3, 2) x+= 2.

; =0, х=1.

tgz= , tgz= , tgz=1.

Z=arctg ()+Πk, kZ, z=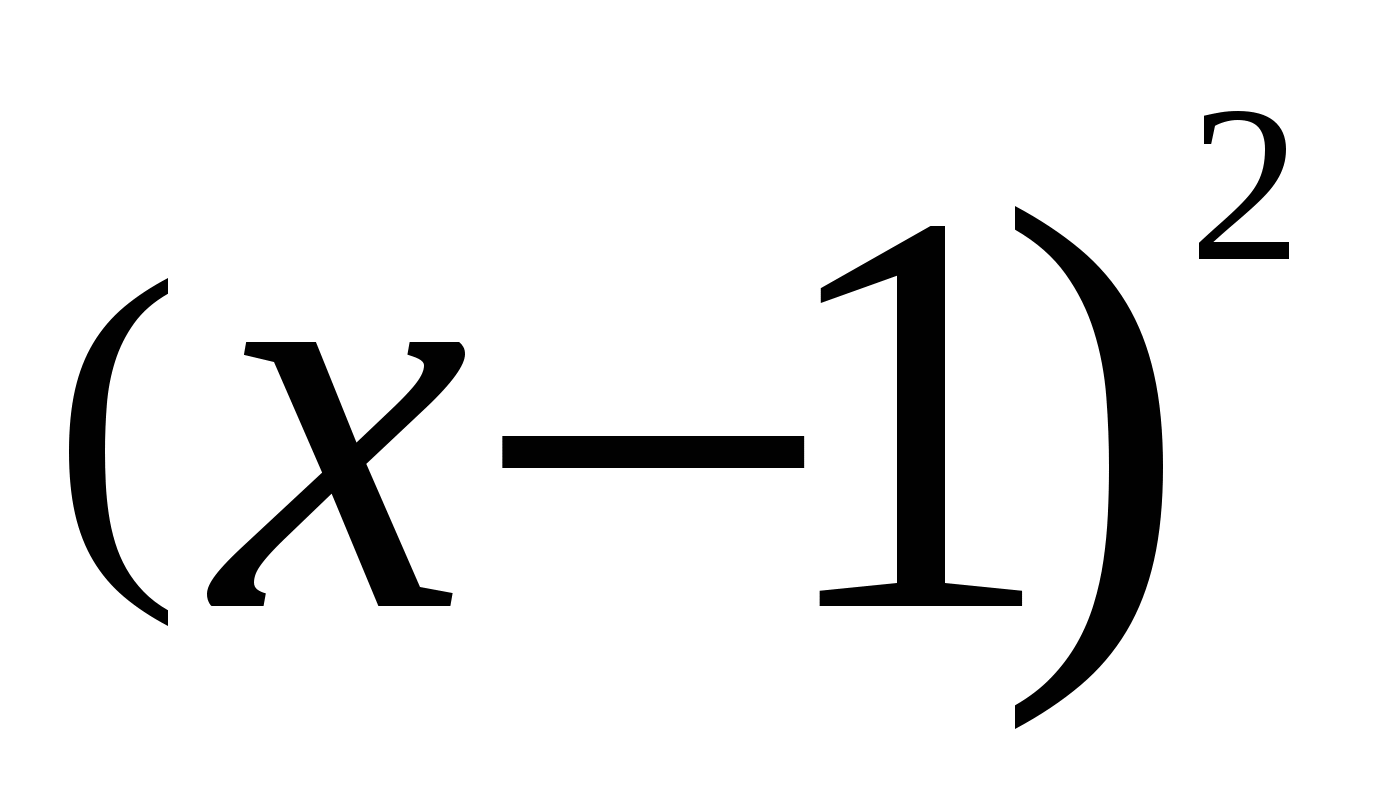

Z=arctg ()+Πm, mZ

Ответ: Z=arctg ()+Πk, kZ, Z=arctg ()+Πm, mZ, z=.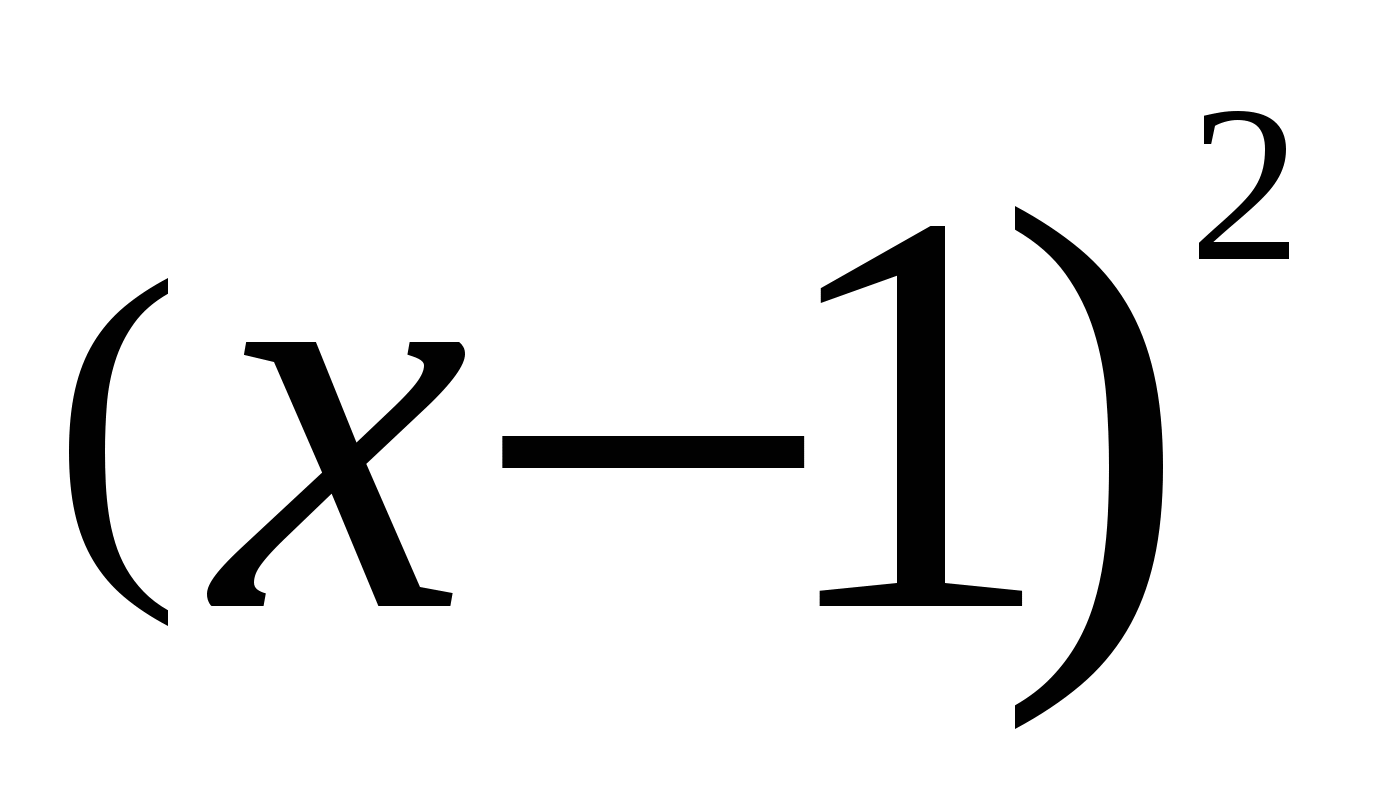

Учитель:

Решая тригонометрическое уравнение, вспомнили способ введения новой переменной, приемы решения симметрического уравнения.

Это пригодится сегодня на уроке.

IV. Актуализация знаний (продолжение), формирование умений (приобретение опыта).

1. Учитель предлагает двум учащимся поработать у доски, задания - на карточках.

Карточка 1.

Разложить многочлен на множители с помощью схемы Горнера.

Примечание.

Ученик подбором находит один корень многочлена (х=1), затем составляя схему Горнера, находит коэффициенты квадратного трехчлена, который является вторым множителем.

1

1

-4

2

1

1

2

-2

0

= (х-1) ()=(х-1)(х+1-) (х+1+).

Карточка 2.

При каких значениях a уравнение имеет два различных корня:

а. Укажите наибольшее целое отрицательное значение.

Примечание.

Ученик анализирует уравнение.

Квадратное уравнение (a≠0) имеет два различных корня при условии D>0.

D=; >0, a(a+4)>0. a(-∞;-4)(0;+ ∞), а = -5.

2.Остальные обучающиеся работают в тетрадях. (Фронтальная работа).

Учащимся ставится задача:

по виду уравнения определить способ (прием) его решения. (В тетрадях записать вид уравнения, указать способы, приемы решения. Подробного решения записывать не надо).

Уравнения - на экране.

1).

Примечание.

Учащиеся подбором находят корень -1.Затем с помощью схемы Горнера - кратный корень 2.

2)118

Примечание.

Учащиеся подбором находят корень 1.Затем с помощью схемы Горнера многочлен в левой части раскладывают на множители и находят второй корень .

3)

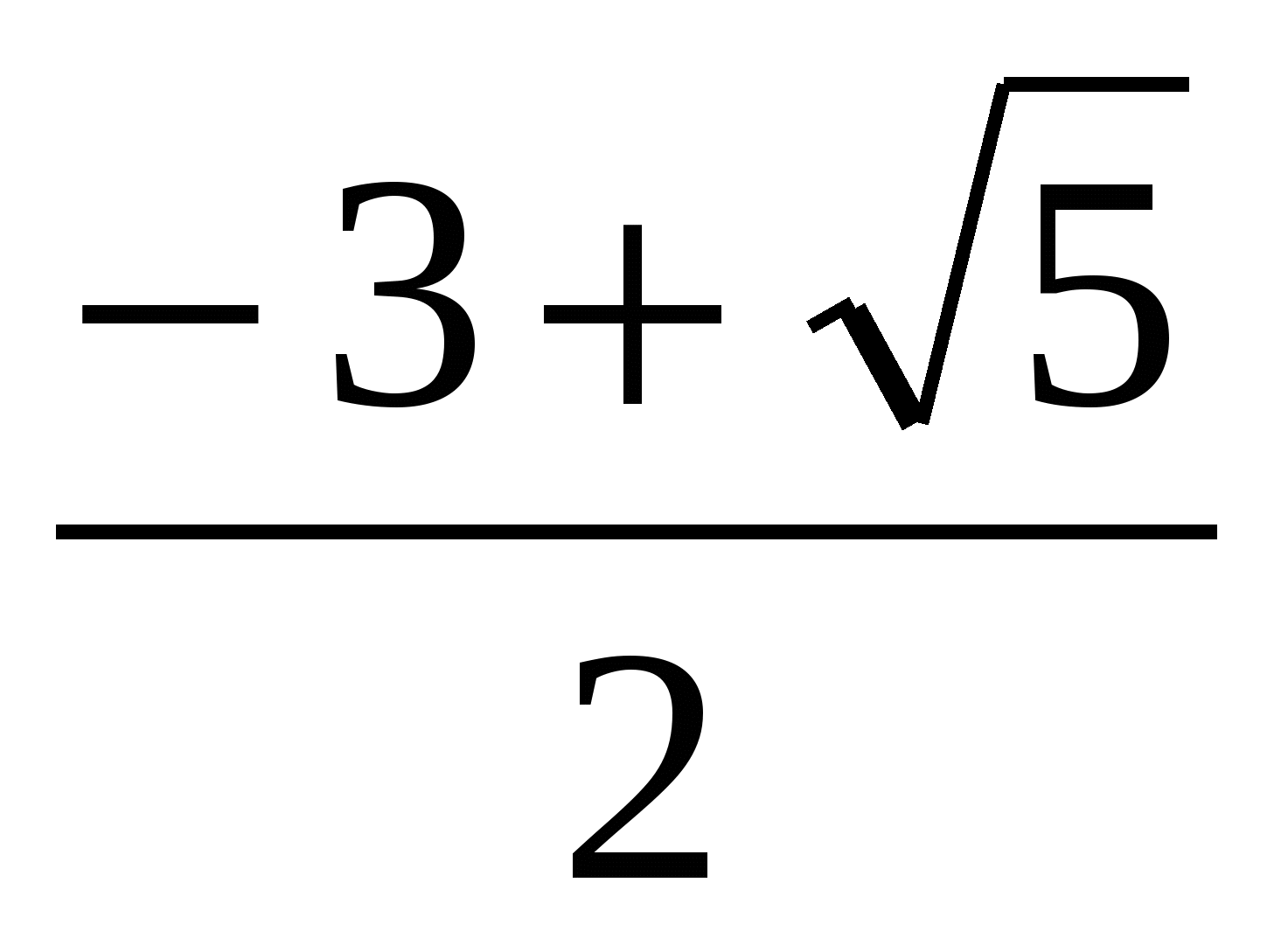
Примечание.

Учащиеся определяют вид уравнения: рациональное алгебраическое.

Вспоминают приемы решения: а)деление числителя и знаменателя на х (х=0 не является корнем); б)введение новой переменной (t = x+).

4)

Примечание.

Учащиеся по виду уравнения вспоминают подстановки:

x = t+m,

x-4=t-m.

5)

Примечание.

Учащиеся называют способ решения: введение новой переменной.

6) .

При каких значениях а уравнение не имеет корней.

Примечание.

Учащиеся, анализируя вид уравнения, устанавливают: при D < 0.

3.Проверка выполнения заданий учащимися на доске. Учащиеся объясняют решение, отвечают на вопросы одноклассников.

Учитель подводит итоги.

Повторили некоторые виды алгебраических уравнений, способы и приемы их решения. Наиболее часто встречается прием: подбор корня, способы: введение новой переменной, разложение многочлена на множители (при этом полезно помнить схему Горнера).

На предыдущих уроках мы еще решали, так называемые, однородные уравнения.

Но вернемся к задаче №1, которая предлагалась в начале урока.

Появились ли предложения по поводу ее решения?

Учащиеся.

- возможно, надо разложить многочлен на множители, используя схему Горнера.

Второй множитель в этом разложении будет квадратным трехчленом, наличие корней которого зависит от дискриминанта.

Учитель.

Задачу №1 попытайтесь решить дома, проверьте свои предположения.

4.Задание на дом.

1)Задача №1;

2)В. №119(3,4) - стр.69;

3)К.№138- стр.284;

4) (Дополнительно) Найти область определения функции: y=arcsin .

V.Продолжаем приобретать опыт, который пригодится при решении нестандартных задач, в том числе и задачи №1.

Работа в группах (6 групп).

Состав групп - прежний. Обсуждаете ход решения. Затем каждый решает сам. Далее сверяете ответы, разбираетесь в ошибках.

После завершения работы над уравнением направляете представителя группы для защиты решения на доске.

Задания для работы в группах.

Решить уравнения.

1) (х>0).

2) (х-4) (х-6) (.

3).

4).

5) .

6) (.

Каждой группе учащихся предложены для решения эти 6 уравнений, указано, решение какого уравнения они должны защитить на доске, (в соответствии с порядковым номером группы, например, группе №1- 1-е уравнение).

Представитель группы выходит готовиться к доске, остальные учащиеся продолжают решать оставшиеся уравнения самостоятельно.

Защита решений.

Представитель у доски кратко комментирует решение своего уравнения, отвечает на вопросы.

VI. Подведение итогов

Учитель

Сегодня на уроке мы повторили основные виды алгебраических уравнений, способы и приемы их решения. (Учитель сообщает отметки учащимся). Вы приобрели дополнительный опыт. Беритесь за любые уравнения. Настойчиво добивайтесь результата. Помните, что говорил Д.Пойа («Если вы хотите научиться плавать, то смело входите в воду, если хотите научиться решать задачи, то решайте их!»).

Приложения.

Приложение 1.

Ответы к заданиям в группах

Уравнение

Ответ

1) (х>0).

(из книги:

Э.О.Зеель. Задачник по алгебре и началам анализа. Архангельск. ПГУ им.М.В.Ломоносова. 2001г.)

0,2; 0,8

2) (х-4) (х-6) (.

-6; 2;

3).

-2,5; -2; 0,5; 1

4).

-3- -3+;

5) .

;

6) (.

-2; 1;

Приложение 2

Решение задачи №1

Найдите наибольшее значение параметра а, при котором уравнение а x +b=0 с целыми коэффициентами имеет три различных корня, один из которых равен -2.

1)Так как -2-корень уравнения, то верно равенство -8+20-2а+в=0, в=2а-12.

2)Разложим многочлен на множители с помощью схемы Горнера.

1

5

а

в=2а-12

-2

1

3

а-6

0

а x +b= (х+2) ().

=0.

D>0 (при этом условии квадратное уравнение имеет два различных корня, значит, данное уравнение а x +b=0, вероятно, будет иметь три различных корня).

D= -4a+33. -4a+33>0; a< < 8.

3) Так как a,b - целые числа, причем значение a- наибольшее, то, возможно, a=8, тогда b = 16-14=4.

Подставим значения a,b в данное уравнение. Решая его, получим корни: -1 и -2 (корень кратности 2). Трех различных корней нет.

Проверим a=7. Получим корни: -2; .

Ответ: a=7.