Урок алгебры в 11 классе по теме «Показательная функция, ее свойства и график».

Урок алгебры в 11 классе по теме «Показательная функция, ее свойства и график».

Учитель: Вакажева Асиет Хазраиловна

Учебник: Мордкович А.Г.

Тема урока: Показательная функция, ее свойства и график (первый урок в теме).

Тип урока: урок формирования новых знаний.

Цель урока:

Образовательная: ввести определение показательной функции, формировать умение строить и преобразовывать графики показательной функции у=а^x (где а>0, a≠1) уметь строить и преобразовывать график показательной функции, рассмотреть ее свойства.

Развивающая: Развитие логического мышления, умения сравнивать и обобщать.

Воспитательная: Воспитание познавательной активности.

Планируемые результаты:

Знать: определение показательной функции, свойства функции в зависимости от основания.

Уметь: строить, читать и преобразовывать графики показательной функции, находить наибольшее и наименьшее значения функции на заданном промежутке.

Используемое оборудование: проектор, компьютер, интерактивная доска

Структура урока:

1. Организационный момент

2. Актуализация опорных знаний

3. Изучение нового материала

4. Закрепление изученного материала

5. Домашнее задание

6. Итог урока

Ход урока.

1. Организационный момент (проверка готовности учащихся к уроку. Организация внимания учащихся.).

2. Актуализация опорных знаний (повторение):

   1. Какие свойства функции вы знаете? (область определения, область значений, монотонность, четность/нечетность, ограниченность, непрерывность, выпуклость, экстремумы)

   2. Какие преобразования графика функции вы знаете?

3. Изучение нового материала:

«Показательная функция, ее свойства и график» (записать в тетрадь).

Построить график функции y=2^x.

Найдем значения функции

при х=0, х=±1, х=±2, х=±3.

x=0, y=2⁰=1; Точка А.

x=1, y=2¹=2; Точка В.

x=2, y=2²=4; Точка С.

x=3, y=2³=8; Точка D.

x=-1, y=2^-1=¹/₂=0,5; Точка K.

x=-2, y=2^-2=¹/₄=0,25; Точка M.

x=-3, y=2^-3=¹/₈=0,125; Точка N

.

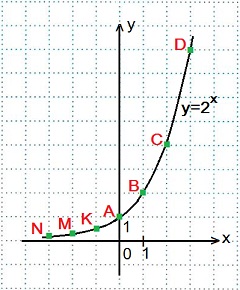
Большему значению аргумента х соответствует большее значение функции у. Функция y=2^x возрастает на всей области определения D (y)=R, так как основание функции 2>1.

2) Построить график функции y=(¹/₂)^x.

Найдем значения функции

при х=0, х=±1, х=±2, х=±3.

x=0, y=(½)⁰=1; Точка A.

x=1, y=(½)¹=½=0,5; Точка B.

x=2, y=(½)²=¼=0,25; Точка C.

x=3, y=(½)³=1/8=0,125; Точка D.

x=-1, y=(½)^-1=2¹=2; Точка K.

x=-2, y=(½)^-2=2²=4; Точка M.

x=-3, y=(½)^-3=2³=8; Точка N.

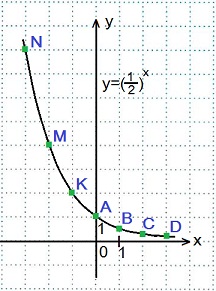
Большему значению аргумента х соответствует меньшее значение функции y. Функция y=(¹/₂)^x убывает на всей своей области определения: D (y)=R, так как основание функции 0<(¹/₂)<1.

.

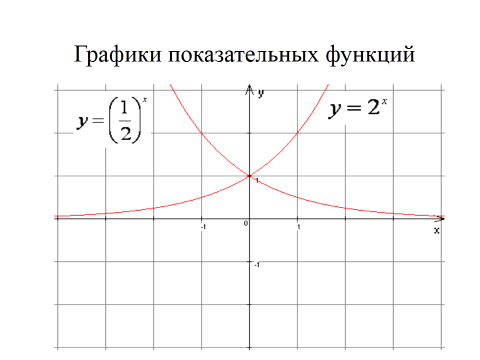
Итак, функция у = а^х, где а>0 и а  1 называется показательной, а ее график - экспонентой.

Почему накладывается условие а > 0 и а  1?

График любой функции у = а^х при а > 1 имеет вид (на рисунке слева), а график любой функции у = а^х при 0 < а < 1 имеет вид (на рисунке справа).).

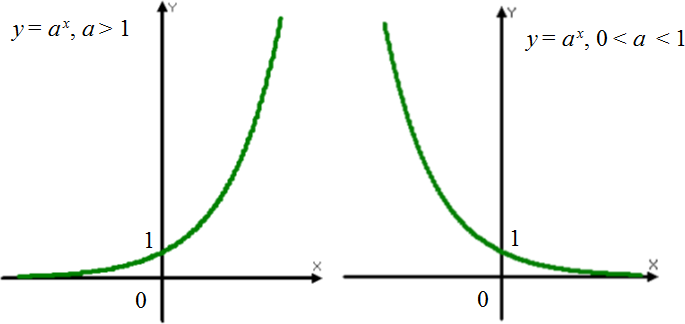
Решить графически уравнения:

1) 3^x=4-x.

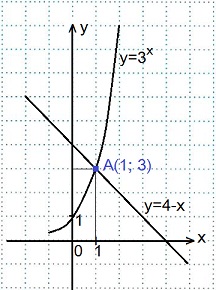
В одной координатной плоскости построим графики функций: у=3^х и у=4-х.

Графики пересеклись в точке А(1; 3). Ответ: 1.

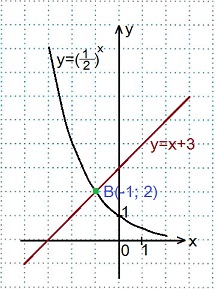
2) 0,5^х=х+3.

</</font>

В одной координатной плоскости строим графики функций: у=0,5^х (y=(¹/₂)^x ) и у=х+3.

Графики пересеклись в точке В(-1; 2). Ответ: -1.

4. Закрепление изученного материала

1. Приведите пример показательной функции.

2. При каком значении а показательная функция возрастает(убывает)?

3. Найти множество значений функции у = 2^х + 3. Почему?

4. Решить по учебнику №39.16(а,б), №39.29(а,б), №39.31(а,б)

5. Домашнее задание п.39, №39.5,39.7,39.7,39.16(в,г), 39.32(а,б).

6. Итоги урока.

4