Иррациональные неравенства (способы решения)

Иррациональные неравенства.

(способы решения)

Определение. Неравенства, содержащие неизвестное под знаком «радикала», называются иррациональными.

( - знак радикала )

Способы решения

1. Графический способ.

2. Алгебраический способ

( использование соответствующих схем )

3. Функциональный способ

(с использованием соответствующих свойств функций).

4. Другие приёмы и методы: замена переменных, метод интервалов, комбинирование способов.

Задача 1. Решите неравенство:

.

Способ 1. Графический.

Построим графики функций:

(1) (2)

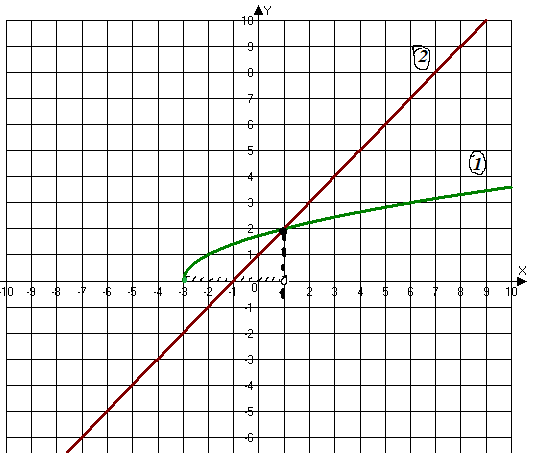
Найдем такие значения x, при которых график функции (1) лежит выше графика функции (2):

Ответ: .

Способ 2. Алгебраический.

1) Если , то неравенство верно на ОДЗ:

2) Если , то возведем обе части неравенства с не отрицательными частями в квадрат, при этом знак неравенства сохраниться.

Получим:

Замечание. В данном случае, условие существования выражения , записывать в систему необязательно, благодаря наличию в ней неравенства .

3) Объединим полученные результаты:

Ответ: .

Краткая запись решения может быть следующей:

или

Объединим полученные результаты:

Ответ: .

Замечание. По аналогичной схеме можно оформлять решение иррациональных неравенств вида:

,

(nнатуральное число)

Способ 3. Замена переменных.

Пусть , тогда , .

Решим систему неравенств:

Тогда:

Ответ: .

Способ 4. (метод интервалов).

Рассмотрим функцию и найдем такие значения х, при которых f(x) > 0.

1) D(f): ;

2) Нули функции:

Решим уравнение

3) (положительное число), значит -3 является решением неравенства.

(так как не является нулём функции, то проверка этого числа на «решение» обязательна)

,

Ответ: [ -3; 1) .

Справочная таблица решения некоторых видов иррациональных неравенствПусть n - натуральное число,

f(x) и g(x) - функции от переменной х.

I. Неравенство вида :

II. Неравенство вида :

III. Неравенство вида :

IY. Неравенство вида :

Y. Неравенство вида :

YI. Неравенство вида :

Замечание. Для решения нестрогих неравенств можно использовать равносильный переход к совокупности, например:

если n=2k, где k - натуральное число, то

Задача 2. Решите неравенство:

.

Решение

Способ 1. (метод интервалов).

Рассмотрим функцию и найдем такие значения х, при которых f(x) ≤ 0.

1) D(f): ;

2) Нули функции:

Решим уравнение

(так как неравенство нестрогое, то нуль функции является решением неравенства)

3) (положительное число), значит -3 не является решением неравенства.

(так как не является нулём функции, то проверка этого числа на «решение» обязательна)

,

Ответ: [1; +)

Способ 2. (по схеме).

Ответ: [1; +)

Задача 3. Решите неравенство:

.

Способ 1. (метод интервалов).

Решение.

Рассмотрим функцию и найдем такие значения х, при которых .

1) D(f):

2) Нули функции: решим уравнение

(так как неравенство нестрогое, то нули функции являются решениями неравенства)

3) ,

Ответ: .

Способ 2. (алгебраический)

1) ОДЗ:

2) Проверим крайнюю точку ОДЗ: решение неравенства (проверка).

3) Если , то .

Учитывая это условие, решим систему:

,

.

4) Объединяем полученные результаты:

.

Ответ: .

Замечание. Обратим внимание на частые рассуждения,

приводящие к потере решений:

т.к. , то , тогда , получаем.

Произошла потеря решения .

Избежать таких ошибок в рассуждениях можно используя равносильный переход к совокупности (см. способ 3).

Один из вариантов оформления предлагается ниже.

Способ 3. (переход к совокупности)

или

или или

нет решений

Ответ: .

Задача 4. Решите неравенство:

.

Способ 1. (метод интервалов).

Рассмотрим функцию и найдем такие значения х, при которых .

1) D(f):

2) Нули функции:

Решим уравнение

(так как неравенство нестрогое, то нули функции являются решениями неравенства)

3) ;

Ответ: .

Способ 2. (алгебраический)

1) ОДЗ:

2) Проверим крайние точки ОДЗ:

а) решение неравенства (проверка);

б) решение неравенства (проверка).

3) Если , то .

Учитывая это условие, решим систему:

,

.

4) Объединяем полученные результаты:

.

Ответ: .

Задача 5. Решите неравенство

.

Способ 1. (метод интервалов).

Решение.

Рассмотрим функцию .

1) D(f):

2) Нули функции:

(посторонний корень уравнения нулем функции не является)

3) ;

Вывод. - решение неравенства

Ответ: .

Способ 2*. ( используeм вспомогательный тригонометрический аргумент).

.

1) ОДЗ:

2) Пусть , тогда , значит .

Решим неравенство:

Учитывая условие , получим

Для решения неравенства воспользуемся методом интервалов, на промежутке

Нули функции:

Функция - возрастающяя на промежутке , поэтому

Ответ: .

Задача 6*.

alexlarin.net/

вариант 130

задача №15

Решите неравенство

.

Способ 1*. (используем вспомогательный тригонометрический аргумент).

1) ОДЗ:

2) Проверим крайние точки ОДЗ:

а) решение неравенства (проверка);

б) не является решением неравенства (проверка).

3) Рассмотрим остальные значения переменной, входящие в ОДЗ, .

Пусть , тогда , значит .

Решим неравенство:

, где ,

Для решения неравенства воспользуемся методом интервалов, на промежутке

Нули функции:

Функция - возрастающяя на интервале , поэтому

4) Объединяем полученные результаты:

Ответ: .

Замечание.

При решении этой задачи можно выполнить и другую замену:

1) ОДЗ:

2) Пусть , тогда , значит .

Решим неравенство:

, где ,

(*)

Для решения неравенства (*) воспользуемся методом интервалов, на промежутке

Нули функции:

нули функции являются решением тригонометрического неравенства (*)

Проверим крайние точки:

- не является решением неравенства (*);

- является решением неравенства (*).

</<font color="#c00000">Вывод:

Функция - убывающая на отрезке , поэтому

Ответ: .

Задача 7*.

Решите неравенство

.

Решение.

Воспользуемся методом, основанным на использовании векторов.

Заметим некоторое сходство каждого из слагаемых данного неравенства с выражением, по которому можно вычислить длину вектора по его координатам

, где .

Пусть и , тогда

и .

Заметим, что , тогда .

Перепишем данное неравенство в виде: , но по свойствам длин векторов .

Вывод: , а такое равенство возможно только в том случае, если вектора и коллинеарные.

Воспользуемся условием коллинеарности двух ненулевых векторов

и , причем ни одна из координат этих векторов в нуль

не обращается:

(единственное решение)

Проверку результата можно выполнить в качестве самоконтроля.

Ответ:

Замечание. Можно увидеть некоторое сходство каждого из слагаемых данного неравенства с выражением, по которому можно вычислить длину отрезка по координатам его концов (расстояние между двумя точками):

.

Тогда возможно введение координат некоторых точек и рассмотрение вопроса о принадлежности этих точек одной прямой.

Такой подход можно применить в некоторых задачах с параметром,

например, связанных с системами уравнений:

№18. Найдите все значения параметра а, при каждом из которых система уравнений

имеет ровно одно решение.

Ответ:

Турков А.Ф.

Заслуженный учитель РФ, учитель математики МАОУ лицей № 38,

г. Нижний Новгород

30.10.2016