Нестандартные задачи по математике с решениями. 7-9 класс. Часть 1.

Интерес к математике и математические способности учащихся проявляются в довольно раннем возрасте. Значительную роль в их развитии играет систематическое решение задач, которые могли бы заинтересовать юных математиков и способствовали бы стремлению к самостоятельным исследованиям.

Именно такие задачи содержит данный сборник. Он предназначен для внеклассных занятий с учащимися 7-9 классов.

В сборнике приведены подробные решения 20 нестандартных задач. Многие из них предлагались на математических олимпиадах.

Данный сборник может служить пособием для подготовки учащихся к олимпиадам по математике.

Задача № 1

Доказать, что если из трехзначного числа вычесть трехзначное число, записанное теми же числами, что и первое, но в обратном порядке, то модуль полученной разности будет делится на 9 и 11.

Решение:

Пусть 100a + 10b + c - трехзначное число, тогда 100с +10b + a - трехзначное число, записанное теми же числами, что и первое, но в обратном порядке.

100a + 10b + c - 100с -10b - a = 99а - 99с = 99(а-с)

|99(а-с)| - делится на 9,

|99(а-с)| - делится на 11,

т.к.очевидно, что 99 будет делиться на 9 и на 11.

Задача № 2

Если между цифрами двузначного числа x вписать это же число, то полученное четырехзначное число будет в 66 раз больше первоначального двузначного. Найти х.

Решение:

Пусть 100a + b = х - данное двузначное число, тогда 1000а +100а + 10b + b - полученное четырехзначное число, что по условию равно (10а + b)/66. Имеем уравнение:

1000а +100а + 10b + b = (10а + b)/66;

1100а + 11b = 660а + 66b;

440а = 55b;

8а = b;

а  0, т.к. а - первая цифра двузначного числа;

а = 1, b = 8, следовательно, x = 18.

а = 2, b = 16, что невозможно, т.к. b - вторая цифра двузначного числа.

Итак, искомое число 18.

Задача № 3

Доказать, что число 333⁵⁵⁵ + 555³³³ делится на 37.

Решение:

. Очевидно, что делится на 37.

Задача № 4

Доказать, что число 11¹¹ + 12¹² + 13¹³ делится на 10.

Решение:

Число 11¹¹ оканчивается единицей. Выясним, какой цифрой оканчивается число 12¹².

12¹ = …2

12² = …4

12³ = …8

12⁴ = …6

12⁵ = …2

12⁶ = …4

…

Отметим, что последняя цифра с возрастанием меняется периодически через 4 последовательных показателя. Т.к. 12 : 4 = 3 раза повторится период, то 12¹² оканчивается цифрой 6. Теперь выясним, какой цифрой оканчивается число 13¹³

13¹ = …3

13² = …9

13³ = …7

13⁴ = …1

13⁵ = …3

13⁶ = …9

…

Аналогично рассуждая, получаем: 13¹³ оканчивается цифрой 3. Складываем последние цифры: 1 + 6 + 3 = 10, значит, число 11¹¹ + 12¹² + 13¹³ оканчивается нулем, следовательно, 11¹¹ + 12¹² + 13¹³ делится на 10.

Задача № 5

Доказать, что число 10¹⁵ + 10¹⁷ - 74 делится на 9.

Решение:

10¹⁵ + 10¹⁷ - 74 = 10¹⁵ - 1¹⁵ + 10¹⁷ - 1¹⁷ + 2 - 74 = (10 - 1) (…) + (10 - 1) (…) - 72 = 9 (…) +

+9 (…) - 98 = 9(… + … - 8) - это число, очевидно, делится на 9.

Задача № 6

Доказать, что при любом целом число делится на 30.

Решение:

. Чтобы произведение делилось на 30, нужно, чтобы оно делилось на 5 и на 6. - произведение трех последовательных чисел, поэтому оно делится на . Итак, чтобы доказать, что делится на 30, осталось доказать, что оно делится на 5.

Если - четное, то его квадрат оканчивается на 4 или 6.

Если оканчивается на 4, то оканчивается на 5.

Если оканчивается на 6, то оканчивается на 5.

Если - нечетное, то оканчивается на 1, или на 9, или на 5.

Если оканчивается на 9, то оканчивается на 0.

Если оканчивается на 1, то оканчивается на 0.

Если оканчивается на 5, то оканчивается на 5.

Значит, делится на 30.

Задача № 7

Доказать, что при любом целом число делится на 120.

Решение:

- произведение пяти последовательных чисел.

120 = . Значит, делится на 120.

Задача № 8

Найти пятизначное число, если известно, что при умножении этого числа на 9 получается пятизначное число, записанное теми же цифрами, но в обратном порядке.

Решение:

- данное пятизначное число.

При умножении на 9 получим: . Т.к. числа пятизначные, то При умножении на 9 число остается пятизначным, поэтому Тогда значит . После умножения на 9 получаем

Т.к. - однозначные числа, то даже если , то правая часть последнего равенства равна поэтому чтобы выполнялось равенство нужно взять . Равенство примет вид:

91 не делится на 8, поэтому делится на 8, значит, . Получаем:

Т.о.

Задача № 9

Доказать, что если - целые числа такие, что число делится на 17, то число также делится на 17.

Решение:

По условию делится на 17, значит делится на 17. делится на 17 очевидно, следовательно, делится на 17, т.е. и также делится на 17.

Задача № 10

Доказать, что сумма квадратов пяти последовательных целых чисел не является квадратом целого числа.

Решение:

Пусть , +1, +2, +3, +4- пять последовательных целых чисел, тогда

Дискриминант этого не равен 0, а значит, что 5 не равно квадрату какого-то целого числа.

Задача № 11

Доказать, что если p простое число, большее трех, то число делится на 24.

Решение:

Пусть p-простое число, . Если делится на 24, то , где k.

По условию р и p - простое число, поэтому р - нечетное. Тогда р1 и р+1 - четные последовательные числа, значит, р1 делится на 2, а р+1 делится на 4, т.е. делится на 8. Так как р простое число , то оно не делится на 3, т.е. р=3k+1 или p=3k+2.

Если p=3k+1, то p1=3k делится на 3 и тогда делится на 3 8=24

Если же p=3k+2, тогда p+1=3k+3 делится на 3 и тогда делится на 3 8=24 , что и требовалось доказать.

Задача № 12

Доказать, что если p простое число и p5, то остаток от деления числа на 12 равен 1.

Решение:

По условию p - простое и p . Чтобы остаток от деления на 12 был равен 1, надо чтобы , где , т.е. - таким образом надо доказать, что делится на 12.

р - простое, не меньше чем 5,поэтому p - нечетное, тогда p - 1 и p + 1 четные последовательные числа, поэтому одно из них делится на 2, другое на 4. Осталось доказать, что делится на 3.

р - простое число, значит на 3 не делится, т.е. оно имеет вид p=3n+1 или p=3n+2, где n. Если p=3n+1, тогда p1=3n - делится на 3, значит и делится на 3.

Если же p=3n+2, то p+1=3n+3 делится на 3. Это значит, что кратно 12: .

, т.е. остаток от деления на 12 равен 1.

Задача № 13

Сколькими нулями оканчивается число, полученное при перемножении всех чисел от 1 до 100?

Решение:

Среди чисел от 1 до 100 содержится десять чисел, оканчивающихся нулями. Это 10, 20, 30, …, 90, 100. Произведение этих чисел оканчивается одиннадцатью нулями. Кроме того, среди чисел от 1 до 100 содержатся числа, оканчивающихся пятеркой это 5, 15, 25, 35,…, 85, 95. Их десять. Каждое из этих чисел при умножении на четное число дает число, оканчивающееся нулем. Итак, еще 10 нулей. Кроме того, числа 25=5, 75=5 и 50=5, имея в разложении еще по пятерке, при умножении на четное число дадут еще три числа, окачивающихся нулями. Значит, произведение всех чисел то 1 до 100 окачиваются 11+10+3=24 нулями.

Задача № 14

Доказать, что если - корни квадратного уравнения , где r0, то выполняется неравенство

Решение:

По теореме

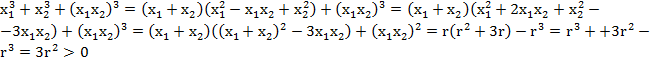при r, что и требовалось доказать.

Задача № 15

Найти все значения r, для которых при действительных значениях x выполняется неравенство

Решение:

Данное неравенство будет выполняться при всех действительных значениях х, если

D=

Решаем систему неравенств:

.

Если же r=1, неравенство принимает вид , т.е. - верно.

Ответ:

Задача № 16

Доказать, что при всех действительных значениях x справедливо неравенство:

Решение:

Данное неравенство равносильно системе неравенств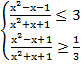

Так как при любом x, то имеем:

Оба неравенства справедливы при всех действительных значениях х. Значит, исходное неравенство справедливо при

Задача № 17

Доказать неравенство

Решение:

=

Задача № 18

Доказать неравенство

Решение:

Задача № 19

Доказать равенство

Решение:

Задача № 20

Доказать равенство

Решение: