Урок математики 8 класс «Квадратное уравнение».

Муниципальное бюджетное общеобразовательное учреждение средняя общеобразовательная школа № 8 поселка им. М. Горького муниципального образования Кавказский район

"… разных детей и учить надо по-разному,
потому что каждый по-своему воспринимает информацию"
Гарднер

Урок по теме «Формула корней квадратного уравнения»

Учитель: Бондарева Т.У., первая квалификационная категория

Класс: 8.

Цель: обеспечить прочное и сознательное овладение учащимися навыками нахождения корней квадратного уравнения по формуле.

Задачи: образовательные: формировать у учащихся умение решать квадратные уравнения (и приводимые к ним уравнения) по формуле; применять теорию (формула дискриминанта, формула корней) в конкретных ситуациях; создать условия контроля (самоконтроля, взаимоконтроля) усвоения знаний и умений; развивающие: развитие логического мышления; развитие устной и письменной речи; формирование навыков владения математическими терминами; воспитательные: формирование личностных качеств: сосредоточенность и внимание; настойчивость и ответственность.

Оборудование и материалы для урока: компьютер, интерактивная доска.

План и ход урока

1. Организационный момент

Приветствие учеников.

Сегодняшний урок мы проведем с использованием рейтинговой системы контроля знаний. У вас имеются оценочные листы, в которых вы выставляете баллы, полученные за каждый этап урока. Каждый правильный ответ оценивается в 1 балл

2. Повторение и закрепление пройденного материала Ответы на вопросы по домашнему заданию (разбор нерешенных задач).

• Контроль усвоения материала (устный опрос).

Задача.

Выполним устно задания, чтобы определить тему и цели урока.

• Дайте определение квадратного уравнения.

• Назовите виды квадратных уравнений.

• Что такое дискриминант? Сколько корней может иметь квадратное уравнение в зависимости от дискриминанта?

• Сколько видов неполных квадратных уравнений существует? Назовите их.

• Из данных уравнений выберите неполные квадратные уравнения: а) х²-6х=0; б) 3х²-11=0; в) х²-х+1=0; г) 8х-х²=0; д) х²=0; е) -х²-5х+2=0 (Ответы записывают в тетрадь и по окончанию работы проверяют на слайдах, за каждый правильный ответ - 1 балл).

• Назовите коэффициенты квадратного уравнения: а) 3x²+7x-6=0; б) 5-3x²-x=0; в) 2y²-11=0; г) x²+7-4x=0; д) 15х-х²=0; е)7c²=0 (Ответы записывают в тетрадь и по окончанию работы проверяют на слайдах, за каждый правильный ответ - 1 балл).

• Замените уравнение равносильным ему приведённым квадратным уравнением: а) 5x²-10x-15=0; б) -x²+2x-2=0 (Ответы записывают в тетрадь и по окончанию работы проверяют на слайдах, за каждый правильный ответ - 1 балл).

• Вычислите дискриминант и определите число корней квадратного уравнения: а) x²+4x-1=0; б) 9x²+6x+1=0; в) x²-3x+5=0 (Ответы записывают в тетрадь и по окончанию работы проверяют на слайдах, за каждый правильный ответ - 1 балл).

Ответы: 1. а, б, г, д. 2. а) а=3, b=7, с=-6; б) а=-3, b=-1, с=5; в) а=2, b=0, с=-11; г) а=1, b=-4, с=7; д) а=-1, b=15, с=0; е) а=7, b=0, с=0. 3. а) x²-2x-3=0; б) x²-2x+2=0. 4. а) D=20, 2 корня; б) D=0, 1 корень; в) D=-11,нет корней.

3. Работа над изученным материалом .

А). Учитель делает анализ выявленных затруднений и предлагает ученикам сформулировать тему и цели урока.

Тема урока: «Формула корней квадратного уравнения»

Цели урока: уметь вычислять дискриминант и сравнивать его с нулем; решать квадратные уравнения с помощью формулы.

Б). Решение задач (у доски).

Задача.

На доске записано уравнение. Назовите коэффициенты. Запишите формулу дискриминанта (D). Вычислите D. Определите: имеет ли уравнение корни. Сколько корней в уравнении? Решите уравнение.

• 5х²-11х+2=0;

Один ученик решает на доске, все остальные самостоятельно в тетради. После того, как уравнение решено, ученик проговаривает решение вслух, а все остальные ребята проверяют записи в тетради.

Задача.

На доске записано следующее уравнение. Сравните. Чем это уравнение отличается от предыдущего? Обратите внимание на коэффициенты. Запишите формулу дискриминанта для четного числа b. Решите уравнение, используя формулу для четного числа b.

• 3х²-14х+16=0;

Один ученик решает на доске, все остальные самостоятельно в тетради. После того, как уравнение решено, ученик проговаривает решение вслух, а все остальные ребята проверяют записи в тетради.

В). Решение разноуровневых задач.

Задача.

На доске записаны уравнения. Я предлагаю в тетради решить их самостоятельно. На решение уравнений дается 4-5 минут. Затем на экран проецирую слайды с правильными ответами (осуществляется взаимопроверка). За каждый правильный ответ - 1 балл. Кто не уложился во времени или выполнил с ошибками, тот остается на том же уровне, а учащиеся, которые справились, получают задания другого уровня.

• Решите уравнение:

а) 2х²-5х-3=0;

б) 3х²-8х+5=0;

в) 5х²=9х+2.

Ответы: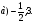

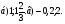
1 группа выполняет работу над ошибками, а 2 группа получает задания:

• Найдите корни уравнения: (2х-3)(5х+1)=2х+.

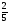• Решите уравнение: 3(х+4)²=10х+32.

• При каких значениях х верно равенство: ?

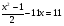Ответы: 1) -0,2; 1,7. 2) 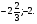3) -1; 23.

Пока учащиеся 2 группы выполняют задания, учитель работает с учащимися 1 группы, разбирая решения уравнений.

Затем проверяются и разбираются задания 2 группы. К рассмотрению решения квадратного уравнения привлекается внимание учащихся 1 группы, чтобы еще раз напомнить алгоритм решения квадратных уравнений по формуле.

С). Разноуровневая самостоятельная работа.

Задача.

Предлагаю в разноуровневой самостоятельной работе проверить умение находить корни квадратных уравнений по формуле.

1 уровень.

• Решите уравнение: у²=52у-576.

• При каких значениях х трехчлен -2х²+5х+6 равен двучлену 4х²+5х?

Ответы: 1) 16; 36. 2) х₁=-1, х₂=1.

2 уровень.

• Решите уравнение: (х-4)(х²+4х+16)+28=х²(х-25).

• Найдите пять последовательных целых чисел, если известно, что сумма квадратов первых трех чисел равна сумме квадратов двух последних.

Ответы: 1) х₁=-1,2; х₂=1,2. 2) -2; -1; 0; 1; 2 или 10; 11; 12; 13; 14.

4. Итог урока .

Определяем вместе: что делали, зачем, к какому результату пришли (считаем количество заработанных баллов). Либо обсуждают в парах: я научился, я узнал нового…, я что-то не понял…. И если при обсуждении в парах кто-то разобрал материал лучше, чем его сосед, он может объяснить своему собеседнику недопонятые моменты еще раз. (Это важный этап, т.к. то, что проговаривает ученик, а если еще и не один раз, лучше запоминается).

5. Домашнее задание

Домашнее задание задается разной сложности, ученик сам выбирает себе задание. Учащиеся со слабыми знаниями по желанию могут тоже выполнять задания повышенной сложности.

1 уровень: № 536(г, д, е), № 537(в), №542(г, е).

2 уровень: №546(в, г), №547(в, г), №662.