- Учителю
- Урок по алгебре для 11 класса по теме «Решение иррациональных уравнений. Подготовка к ЕГЭ»
Урок по алгебре для 11 класса по теме «Решение иррациональных уравнений. Подготовка к ЕГЭ»
Муниципальное Бюджетное Общеобразовательное Учреждение Средняя Общеобразовательная Школа №7 П. Октябрьский Курганинский район
Открытый урок в 11 классе на тему
«Решение иррациональных уравнений. Подготовка к ЕГЭ»
Учитель математики
Тютюнникова
Ирина Николаевна
2013 г
Цели урока:
-
Обобщение и систематизация знаний и умений учащихся по теме «Решение иррациональных уравнений»; формирование умения применять полученные знания при решении задач;
-
Развитие самостоятельности при выполнении конкретных заданий, развитие навыков работы в группе.
Оборудование: презентация «Решение иррациональных уравнений»,
разноуровневые карточки для 1, 2 и 3 групп.
Ход урока
-
Организационный момент.
Учитель сообщает учащимся тему урока, цель и поясняет, что во время урока постепенно будет использоваться тот раздаточный материал, который находится на партах ( в конвертах индивидуальные задания для учащихся распечатаны на цветных карточках согласно уровню их подготовки).
-
Повторение теоретического материала по теме: «Арифметический корень и его свойства. Иррациональные уравнения».
Учитель поясняет учащимся, что прежде чем решать иррациональные уравнения необходимо вспомнить весь теоретический материал на котором базируется решение иррациональных уравнений.
-
Сформулируйте определение арифметического корня натуральной степени?
Ответ: арифметическим корнем n-й степени из числа a называют число, n-я степень которого равна a.
-
Для каких значений а это определение имеет смысл? Как это связано с показателем n?
Ответ: Если n-четное, то а 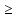 0, в противном случае корень не существует.
0, в противном случае корень не существует.
Если n-нечетное, то а - любое и 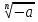 =
= 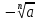 .
.
-
Перечислить основные свойства корня n-ой степени
1.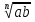 =
=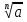

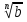
2. 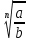 =
=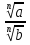 , ( b
, ( b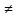 0 )
0 )
-
(
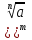 =
= 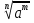 , ( если m
, ( если m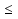 0 , то a
0 , то a 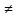 0)
0) -
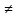 =
= 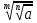
-
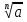 =
= 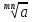 , (k
, (k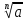 0)
0) -
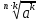 =
=  , если n - четно;
, если n - четно;
a , если n-нечетно.
Если учащиеся не называют какое -либо свойство, то его напоминает учитель.
-
Дайте определение иррационального уравнения?
Ответ: уравнения, в которых под знаком корня содержится переменная, называют иррациональным.
Учитель предлагает рассмотреть примеры иррациональных уравнений.
Примеры: 1) 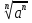 =2, 2)
=2, 2) 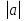 = 3 , 3)
= 3 , 3) 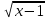 = х - 8,
= х - 8,
4) 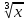 = 2, 5)
= 2, 5) 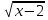 - 6 =
- 6 = 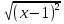 .
.
5. Какие уравнения называются равносильными?
Ответ: 1) уравнения, имеющие одно и то же множество корней, называются равносильными.
2) Два уравнения с одной переменной f (x) = 0 и g (x) = 0 называют равносильными, если множества их корней совпадают.
6. Привести примеры равносильных и не равносильных уравнений?
Учащиеся приводят примеры. Учитель приготовил примеры соответствующих уравнений и после ответов учеников демонстрирует их.
Примеры: 1) уравнения 5х - 6 = 3х + 1 и 2х = 7 - равносильны;
2) уравнения ( х-1) (х + 3) = 0 и  + 2х - 3 = 0 - равносильны;
+ 2х - 3 = 0 - равносильны;
3) уравнения 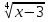 = 0 и
= 0 и  = - 7 - равносильны, т. к. оба не имеют корней;
= - 7 - равносильны, т. к. оба не имеют корней;
4) 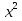 = х - 2 и х =
= х - 2 и х = 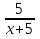 - не равносильны, второе уравнение является следствием первого, т. к. первое имеет один корень х = 4 , а второе два корня х =4 и х = 1.
- не равносильны, второе уравнение является следствием первого, т. к. первое имеет один корень х = 4 , а второе два корня х =4 и х = 1.
5) Учитель обращается к учащимся с вопросом: « Рассмотрим уравнение вида 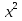 =g(x). Как можно получить из него уравнение, равносильное данному? Какие способы решения уравнений такого типа вы знаете?»
=g(x). Как можно получить из него уравнение, равносильное данному? Какие способы решения уравнений такого типа вы знаете?»
Ответ: учащиеся могут привести два способа решения данного уравнения:
А) Переход к равносильной системе
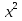 =g(x)
=g(x) 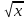 g(x)
g(x) 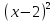
f (x) = 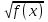 (x)
(x)
Б) Возвести в квадрат данное уравнение, решить уравнение f (x) = 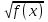 (x).
(x).
Проверить какой из полученных корней удовлетворяет уравнению
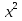 =g(x).
=g(x).
6) Учитель предлагает учащимся рассмотреть уравнение вида 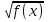 = g(x) и прокомментировать его решение, ссылаясь на соответствующие понятия корня.
= g(x) и прокомментировать его решение, ссылаясь на соответствующие понятия корня.
Ответ: уравнение 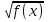 = g(x) равносильно уравнению f (x) =
= g(x) равносильно уравнению f (x) = 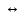 (x) , т. к. корень нечетной степени существует из любого действительного числа.
(x) , т. к. корень нечетной степени существует из любого действительного числа.
Учитель обобщает прозвучавшие ответы на случай произвольного показателя корня.
Для любого натурального значения n справедливы равносильные переходы
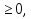 = g(x)
= g(x) 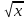 g(x)
g(x) 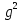 ,
,
f (x) = 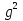 (x)
(x)
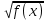 = g(x)
= g(x) 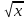 f (x) =
f (x) = 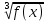 (x)
(x)
Учитель предлагает учащимся воспользоваться рассмотренными теоретическими фактами и решить несколько уравнений устно:
-
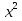 = 5, 2.
= 5, 2. 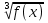 = 2 , 3.
= 2 , 3. 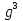 = 3 . 4.
= 3 . 4. 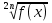 = 2.
= 2.
-
Работа в разноуровневых группах.
Со всеми учащимися класса рассматриваются решения уравнений.
1.Решите уравнение: 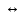 = х - 2
= х - 2
Учащиеся могут привести одно из представленных решений:
а) используя переход к равносильной системе:
4 + 2х -  = (
= ( ,
,  - 6х = 0 , х = 0,
- 6х = 0 , х = 0,
х - 2 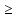 0; х
0; х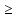 2; х = 3, х = 3.
2; х = 3, х = 3.
х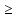 2;
2;
Ответ: 3.
Б) выполняя проверку найденных корней уравнения:
4 + 2х -  = (
= (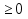 , 4 + 2х -
, 4 + 2х -  =
=  - 4х + 4,
- 4х + 4,
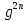 - 6х = 0, 2х( х - 3) = 0, х = 0 или х = 3.
- 6х = 0, 2х( х - 3) = 0, х = 0 или х = 3.
Проверка
-
х = 0,
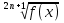 = 0 - 2,
= 0 - 2,  = - 2 неверно.
= - 2 неверно. -
х = 3,
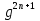 = 3 - 1.
= 3 - 1. 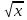 = 1 верно.
= 1 верно.
Значит, 3 - корень уравнения 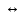 = х - 2
= х - 2
Ответ: 3.
2.Решите уравнение: (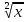 - 3
- 3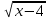 - 10 = 0
- 10 = 0
Решение. Пусть 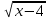 = t , t
= t , t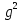 , тогда уравнение имеет вид
, тогда уравнение имеет вид
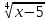 - 3t - 10 = 0, отсюда t = 5 или t = - 2, что не удовлетворяет условию t
- 3t - 10 = 0, отсюда t = 5 или t = - 2, что не удовлетворяет условию t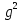 . Тогда
. Тогда 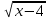 = 5 , х + 3 = 25, х = 22.
= 5 , х + 3 = 25, х = 22.
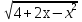 : 22.
: 22.
Далее первая группа учащихся самостоятельно выполняет задания ( зеленая карточка № 1 из индивидуального конверта) , а в это время учитель с учащимися второй и третьей группы рассматривает задания повышенного уровня сложности.
-
Решите уравнение:
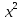 +
+ 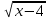 =
= 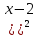
Решение: 1) Найдем ОДЗ: х - 5 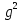
х + 3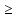 0 ,
0 , 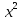 х
х 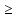 5.
5.
2х + 4 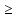 0
0
-
Возведем обе части уравнения в квадрат
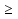 =
= 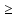 , х - 5 + 2
, х - 5 + 2 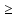
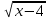 +х + 3 = 2х + 4,
+х + 3 = 2х + 4,
2х - 2 + 2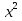 =2х +4, 2
=2х +4, 2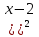 = 6,
= 6,
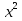 ,
, 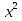 - 24 = 0, отсюда
- 24 = 0, отсюда 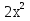 = - 4,
= - 4, 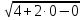 = 6.
= 6.
Так как х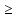 5, то х = - 4 является посторонним корнем.
5, то х = - 4 является посторонним корнем.
Ответ: 6.
Учитель предлагает учащимся второй группы приступить к самостоятельному выполнению заданий ( голубая карточка №1 из индивидуального пакета).
С учащимися третьей группы учитель рассматривает решение уравнения.
4.Решите уравнение: 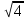 - 1 = 3
- 1 = 3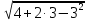
Решение: 1) Преобразуем уравнение 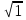 - 1 = 3
- 1 = 3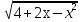 ,
,
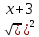 - 1 = 3
- 1 = 3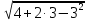 ,
, 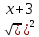 = 3
= 3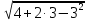 + 1.
+ 1.
ОДЗ: 2х - 10 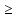 0 , х
0 , х 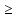 5.
5.
Учитывая ОДЗ, имеем : х - 4 = 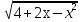 + 1.
+ 1.
2) Решим полученное уравнение: х - 5= 3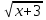 ,
,
(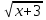 = 3
= 3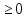
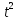 , отсюда х = 5 или
, отсюда х = 5 или 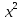 = 3
= 3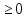 ,
,
х - 5 = 18, х = 23.
Оба корня удовлетворяют ОДЗ.
Ответ: 5; 23.
Далее учащиеся третьей группы выполняют свое задание самостоятельно ( розовая карточка № 1 из индивидуального конверта).
Учитель проверяет правильность выполнения заданий у учащихся первой и второй групп, производится корректировка решений отдельных учащихся ( если появляется необходимость).
Проверка ответов производится с использованием презентации, на слайдах которой записаны верные ответы.
По завершению проверки со всеми учащимися класса рассматривается следующее задание:
-
Решите уравнение: (
 - 9х + 14)
- 9х + 14) 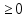 = 0, если уравнение имеет более одного корня , то в ответе указать их произведение.
= 0, если уравнение имеет более одного корня , то в ответе указать их произведение.
Решение: 1) Поскольку произведение нескольких выражений равно нулю, если хотя бы одно из выражений равно нулю, а другое при этом имеет смысл, то
а) ( - 9х + 14)
- 9х + 14) 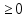 = 0,
= 0, 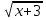 - 9х + 14 = 0 ,
- 9х + 14 = 0 ,
 - 9
- 9 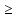 0
0
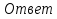 (х - 2) (х -7) = 0
(х - 2) (х -7) = 0  х = 7;
х = 7;
х 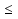 - 3
- 3
х 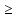 3,
3,
б)  - 9 = 0, отсюда х =
- 9 = 0, отсюда х = 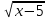 3
3
в) (-3)  3
3  7 =- 63
7 =- 63
Ответ: - 63.
Учитель предлагает учащимся первой группы приступить к самостоятельному выполнению заданий (зеленая карточка №2 из индивидуального конверта).
С учащимися второй и третьей группы учитель рассматривает решение уравнения.
-
Решите уравнение: (
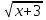 +
+  =
= 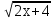
Решение: 1) Преобразуем уравнение к виду:
( 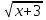 +
+  =
= 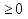 , (
, ( 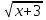 +
+  =
= 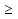 .
.
Учитывая , что 2х - 7 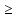 0, х
0, х 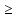
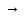 , имеем: 2х - 7 +
, имеем: 2х - 7 +  = 5х - 3,
= 5х - 3,
 - 3х - 4 = 0.
- 3х - 4 = 0.
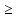 Решим полученное уравнение:
Решим полученное уравнение:  - 3х - 4 = 0, по теореме, обратной теореме Виета, имеем
- 3х - 4 = 0, по теореме, обратной теореме Виета, имеем 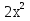 = -1,
= -1, 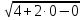 = 4
= 4
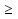 х
х 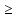
 , имеем х = 4.
, имеем х = 4.
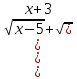
Далее вторая и третья группы учащихся самостоятельно выполняют задания (голубая карточка №2 и розовая карточка №2 из индивидуального конверта).
Пока учащиеся второй и третьей группы выполняют задания, учитель проверяет решения учащихся первой группы, комментирует их при необходимости. После чего проверяются ответы у учащихся второй и третьей групп. Все верные ответы на слайде.
-
Разноуровневая самостоятельная работа
Учитель предлагает учащимся вынуть из конверта карточки с номером 3 для выполнения самостоятельной работы
( см.приложение).
Зеленая карточка №3 (1 вариант)
-
Решить уравнение А)
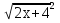 =
=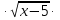 ;
;
Б)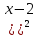 = х-2; В)
= х-2; В) 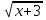 =11.
=11.
2. Решить уравнение (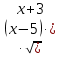 )
)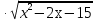 =0, если уравнение имеет более одного корня, то в ответе указать их произведение.
=0, если уравнение имеет более одного корня, то в ответе указать их произведение.
Зеленая карточка №3 (2 вариант)
-
Решить уравнения: А)
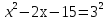 = 4;
= 4;
Б) 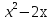 = -3х; В)
= -3х; В)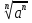 = х - 3.
= х - 3.
2. Решить уравнение (х + 1,5)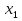 )=0, если уравнение имеет более одного корня, то в ответе указать их произведение.
)=0, если уравнение имеет более одного корня, то в ответе указать их произведение.
Голубая карточка №3 (1 вариант)
1.Решите уравнения: А) 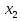 = х - 5;
= х - 5;
Б)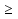 -
- 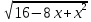 = 2
= 2
2.Решите уравнение (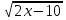 -х) (
-х) ( - 9) = 0, если уравнение имеет более одного корня, то в ответе указать их сумму.
- 9) = 0, если уравнение имеет более одного корня, то в ответе указать их сумму.
3.(С) Решите уравнение (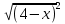 +
+ =
=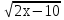 .
.
Голубая карточка №3 (2 вариант)
1. Решите уравнения: А) 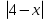 = х - 2
= х - 2
Б) 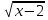 = 1 +
= 1 + 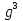
2. Решите уравнение (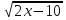 - х) (
- х) ( - 4 ) = 0, если уравнение имеет более одного корня, то в ответе укажите их произведение.
- 4 ) = 0, если уравнение имеет более одного корня, то в ответе укажите их произведение.
3. (С) Решите уравнение (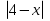 +
+ 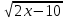 =
=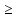 .
.
Розовая карточка № 3 (1 вариант)
-
Решите уравнение (
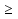 - х - 1)
- х - 1) (4 -
(4 -  ) = 0, если уравнение имеет более одного корня, то в ответе указать их сумму.
) = 0, если уравнение имеет более одного корня, то в ответе указать их сумму. -
(С) Решите уравнение
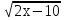 - 2 -
- 2 - 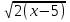 = 0
= 0 -
(С) Решите уравнение (
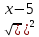 +
+  =
= 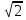
Розовая карточка № 3 (2 вариант)
-
Решите уравнение (
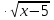 -х + 1)
-х + 1)  (
( - 9 ) = 0, если уравнение имеет более одного корня, то в ответе указать их произведение.
- 9 ) = 0, если уравнение имеет более одного корня, то в ответе указать их произведение. -
(С) Решите уравнение
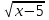 - 1 =
- 1 = 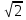
-
(С) Решите уравнение (
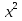 +
+ 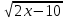 = 7
= 7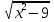
Ответы на задания самостоятельной работы:
Зеленая карточка №3
Номер задания
Вариант №1
Вариант №2
-
А)
2
- 2
1.Б)
0; 6
- 0,4
-
В)
18
2; 5
2.
- 33
7,5
Голубая карточка №3
Номер задания
Вариант №1
Вариант№2
-
А)
3; 8
1; 5
-
Б)
7
4
2.
5
-28
3.
5
1
Розовая карточка № 3
Номер задания
Вариант №1
Вариант№2
1.
3
-7
2.
5; 7
3; 4,5
3.
-2; 3
1
-
Итоги урока.
Учитель обращает внимание учащихся на те теоретические факты и типы уравнений, которые вспомнили на уроке, говорит о необходимости их выучить.
Отмечает наиболее успешную работу на уроке отдельных учащихся, выставляет оценки.
В качестве Д\З учащиеся обмениваются вариантами самостоятельной работы и каждый ученик получает индивидуальное задание.