План урока по геометрии на тему Площади плоских фигур подготовка к ЕГЭ (10 класс)

Муниципальное бюджетное образовательное учреждение

Средняя общеобразовательная школа селения Ир

УРОК ПО ГЕОМЕТРИИ

10 класс

Тема «Подготовка к ЕГЭ.

Нахождение площадей плоских фигур».

Разработала

Разработала учитель математики

МБОУ СОШ с.Ир

Тигиева Тамара Георгиевна

Тема урока:

Подготовка к ЕГЭ. Нахождение площадей плоских фигур.

Решение заданий В4,В8 (обобщающий урок)

Цели урока:

-подготовка учащихся к успешной сдаче егэ;

-систематизация знаний, умений и навыков по нахождению площадей

различных фигур.

Задача урока:

1. Образовательные:

-совершенствовать навыки вычисления площадей фигур ;

-углублять и систематизировать знания учащихся по этой теме.

2.Развивающие :

-способствовать развитию мышления, умения применять полученные

знания при решении задач различной направленности.

3.Воспитательные:

-воспитывать ответственность, коллективизм, взаимопомощь;

Ход урока.

1. Организационная часть урока

а) Приветствие

б) Объявление темы урока и цели

в) Эпиграф к уроку: не мыслям надобно учиться, а мыслить. Кант

2. Повторение. Устный счет.

a)Log 9 81=х(2)

б)Найти 15% от 20000(3000)

в)5log

5

7=x(7)

г)2,7*10-5 / 9*10-4 (0,03)

3. Проверка домашнего задания:

Проектная работа « Моя комната»

Проектная работа « Спортивная площадка»

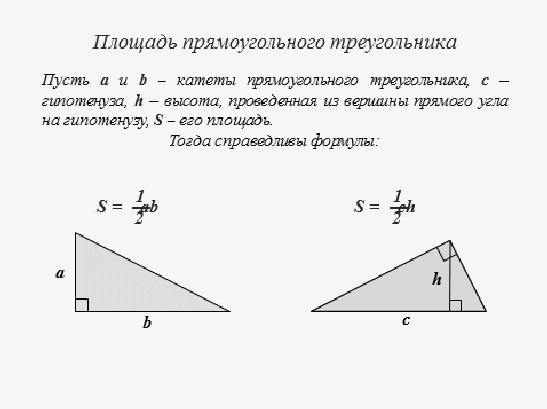
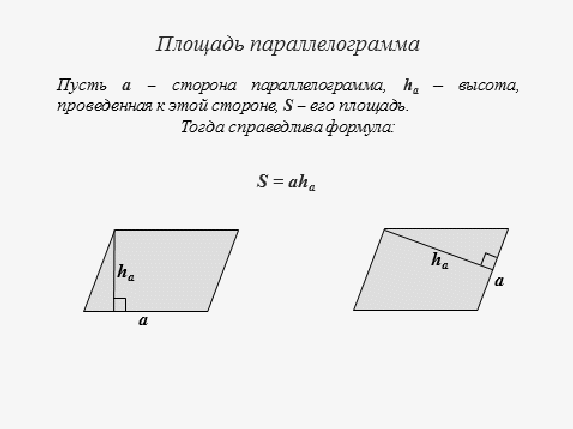
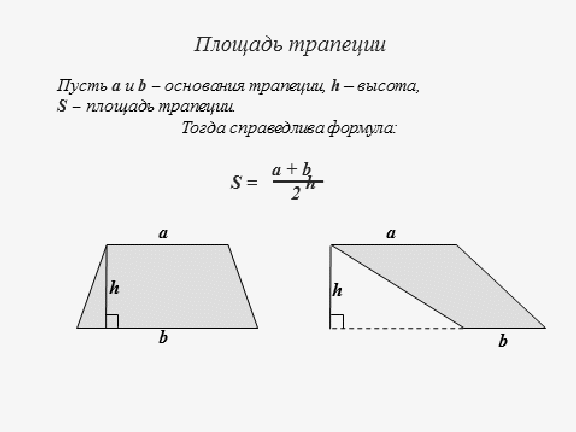
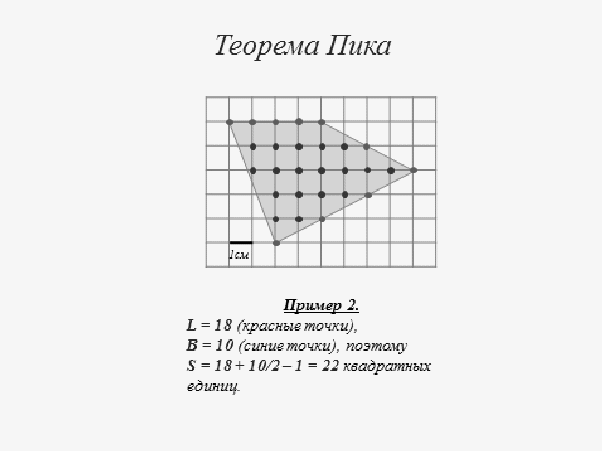
4. Повторение теории: Формулы для вычисления площадей различных фигур.

5. Реферат « Лейбниц».

Интеграл, интеграция, интегрирование…Однокоренные слова, к тому же

вышедшие за пределы математики и ставшие почти обиходными. В газетах

читаем об интеграции наук, культур, в политике и экономике ведут речь об

интегральных процессах. Любопытно, что идеи интегрального исчисления

возникли задолго до появления идей дифференциального исчисления.

Греческие математики Эвдокс и Архимед(4-3 вв. до н.э.) для решения задач

вычисления площадей и объемов придумали разбивать фигуру на бесконечно

большое число бесконечно малых частей и искомую площадь или объем

вычислили как сумму площадей или объемов полученных элементарных

объемов.

Во второй половине 17-го века идеи подготовленные всем

предшествующим развитиям математики были гениально осознанны,

обобщены и приведены в систему английским физиком и математиком

И.Ньютоном и немецким математикам Лейбницем.

Готфрид Вильгельм Лейбниц родился в 1646 году, умер в 1716 году. Он

один из самых многосторонних ученных и глубоких философов Запада.

Юрист, историк, дипломат, физик, математик, филосов, теолог и филолог. Во

всех этих областях Лейбниц был не только глубоким знатоком, но и сам

содействовал дальнейшему развитию науки, внося в неё оригинальные

мысли и планы.

Именно по плану Лейбница была открыта академия наук в Санкт-

Петербурге и в Берлине. А математикой он серьёзно начал заниматься в 26

лет. Он писал: «Я понял, что познать законы мира и бытия можно только с

помощью математики». Лейбниц был уверен, что всё в мире подчинено

определённым математическим законам, а так как человек-частица мира, то

он не исключение. Он хотел найти математический закон взаимоотношений

между людьми, с помощью которого люди бы лучше понимали друг друга.

Может придёт когда-нибудь гений, найдёт эту формулу и на земле

воцарится мир и не будет воин, подобных войнам на Украине, Ливане,

Сирии.

6. Физминутка.

7. Решение задач в тетрадях.

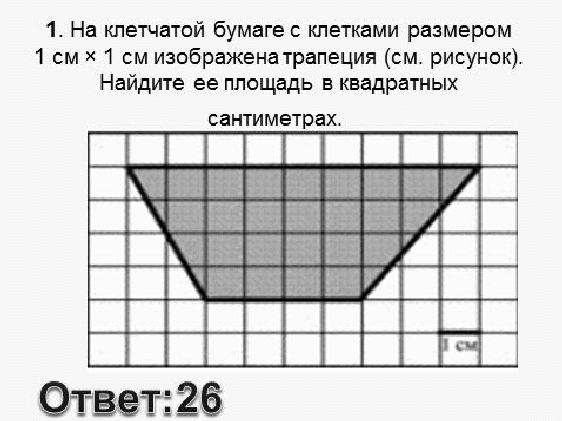
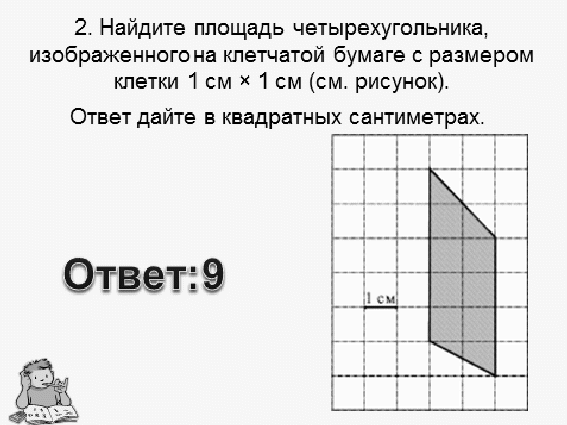
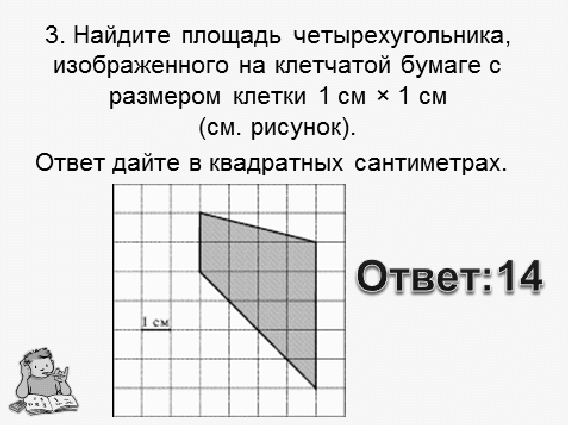
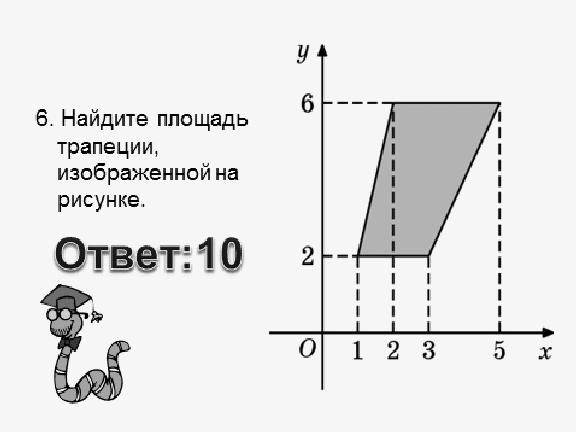
8. Итог урока.

Что мы нового узнали на этом уроке?

Огласить оценки учащихся за урок

9. Домашнее задание.

Профильный уровень: Тест №30

Базовый уровень: Тест №7 В1-

2016 год.