Урок по теме Метод математической индукции

Урок № 50

Тема урока: Метод математической индукции.

Цель урока: Познакомиться с сущностью метода математической индукции, научитесь применять этот метод при решении задач на доказательство, продолжить развитие вычислительных навыков, продолжить формирование математической грамотности.

Ход урока.

1. Организационный момент. Постановка целей урока

2. Активизация опорных знаний.

- Определение геометрической прогрессии, формулы n-го члена геометрической прогрессии.

- Повторить формулу суммы n первых членов арифметической прогрессии.

- Повторить формулу суммы бесконечно убывающей геометрической прогрессии

3. Изучение нового материала

При решении многих задач, при доказательстве справедливости математических предложений, а также при выводе формулы часто используется рассуждение, которое называется методом математической индукции.

Такое рассуждение вы, например, использовали при выводе формулы n-го члена, а также при выводе формулы суммы первых n членов арифметической и геометрической прогрессий.

Сущность этого метода заключается в следующем: если надо установить справедливость некоторого утверждения, в которой фигурирует натуральное число n, то:

1) проверяется, что предполагаемое утверждение имеет место для конкретного значения n (например для n=1).

2) предполагается, что утверждение справедливо при каком-нибудь произвольном значении n = k, и доказывается, что в таком случае оно справедливо и при n = k + 1. Отсюда делается вывод, что утверждение справедливо при любом значении n, ибо справедливость его была обнаружена при n=1, а по доказанному оно верно и при n = 2, а раз справедливо при n = 2, то справедливо и при n = 3 и т.д.

Теперь рассмотрим примеры использования данного метода.

Пример 1. Докажем, что при всяком натуральном n имеет место равенство

Формула верна для n = 1, так как:

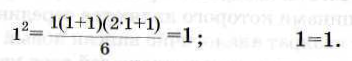
Допустим, что формула верна при п = k.

Докажем, что в таком случае она верна и при n = k + 1, т.е.

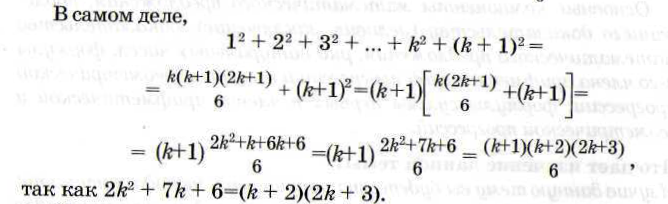
Непосредственная проверка показала, что формула верна при n=1; следовательно, она будет справедлива также при n = 2, а потому и при n = 3, следовательно, и при п = 4 и вообще при любом натуральном n.

4.Решение задач

№249 (а)

В данной задаче требуется доказать формулу n -го члена арифметической прогрессии методом математической индукции

1. При n=1 имеем а₁=а_1.

2. Допустим, что данная формула верна для k-го члена, т.е имеет место равенство а_k=a₁+d(k-1)

3. Докажем, что в данном случае эта формула верна и для (k+1)-го члена. Действительно,

а_k+1=a₁+d(k+1-1) = а₁+dk

С другой стороны, по определению ариф. прогр. а_{k+1 =} а_k+d

Так как левые части двух последних выражений равны = и правые равны:

а_k+d = а₁+dk или а_k = a₁+d(k-1)

Полученное верное равенство позволяет утверждать, что формула n-го члена арифметической прогрессии подходит для любого натурального n

№ 255

Докажем, что число 11ⁿ⁺¹+12^2n-1 при всех натуральных значениях n делиться на 133

1. При n=1 имеем 11¹⁺¹+12^2*1-1=133, 133 делиться на 133

2. Допустим, что при n=k сумма 11^k+1+12^2k-1 делиться на 133

3. Докажем, что эта сумма делиться на 133 при n=k+1, т.е. 11^k+2+12^2k+1 делиться на 133

11^k+2+12^2k+1=11*11^k+1+144*12^k-1=11*11^k+1+11*12^2k-1+133*12^2k-1=11(11^k+1+12^2k-1)+133*12^2k-1

Каждое слагаемое полученной суммы делиться на 133. Следовательно, 11^k+2+12^2k+1 тоже делить на 133.

5. Рефлексия

6. Постановка Д/з

§15 решить №251