Рабочая программа по алгебре , учебник А .Г. Мордкович

Структура рабочей программы

1. Пояснительная записка.

2. Содержание рабочей программы.

3. Учебно-тематический план.

4. Требование к уровню подготовки обучающихся по окончании учебного года.

5. Литература и средства обучения.

6. Тематическое планирование.

1.Пояснительная записка/

Рабочая программа составлена с учётом примерной программы основного общего образования по математике и авторской программы А.Г. Мордковича для общеобразовательных учреждений.(Программы. Математика. 5-6 кл. Алгебра 7 - 9 классы. Алгебра и начала мат анализа 10 - 11 классы. / авт -сост. И.И. Зубарева, А.Г. Мордкович.. 24-е изд., -М.: Мнемозина, 2009. - 63 с.

Основным учебным пособием для обучающихся является:

• Мордкович А.Г. Алгебра. 8 кл.: В двух частях. Ч.1: Учебник для общеобразоват. учреждений. - 16-е изд. -М.: Мнемозина, 2013. - 215 с.: ил.

• Мордкович А.Г. и др. Алгебра. 8 кл.: В двух частях. Ч.2: Задачник для общеобразоват. Учреждений/А.Г.Мордкович, Т.Н.Мишустина, Е.Е. Тульчинчкая. -16-е изд.,доп. -М.: Мнемозина, 2013. - 280 с.: ил

Выбранный учебник входит в логически завершенную линию алгебры А.Г.Мордковича и является логическим продолжением курса алгебры в 7 классе.

Для обучения в 7-9 классах выбрана содержательная линия А.Г.Мордковича, рассчитанная на 3 года. В восьмом классе реализуется второй год обучения. Учебным планом школы на 2016-17 учебный год выделено 102 часа (3 часа в неделю). Автором учебника, А.Г.Мордкович, разработано тематическое планирование, рассчитанное на 3 часа в неделю.

Отличительных особенностей рабочей программы по сравнению с примерной нет.

Срок реализации рабочей учебной программы - один учебный год.

В данном классе ведущими методами обучения предмету являются: поисковый, объяснительно-иллюстративный и репродуктивный. На уроках используются элементы следующих технологий: личностно ориентированное обучение, обучение с применением опорных схем, ИКТ.

Уровень обучения: базовый.

Формы промежуточной и итоговой аттестации.

Промежуточная аттестация проводится в форме контрольных, самостоятельных работ. Итоговая аттестация предусмотрена в виде переводного экзамена.

Для жизни в современном обществе важным является формирование математического стиля общения, проявляющегося в определенных умственных навыках. В процессе математической деятельности в арсенал приемов и методов человеческого мышления естественным образом включаются индукция и дедукция, обобщение и конкретизация, анализ и синтез, классификация и систематизация, абстрагирование и аналогия. Объекты математических умозаключений и правила их конструирования вскрывают механизм логических построений, вырабатывают умения формулировать, обосновывать и доказывать суждения, тем самым развивают логическое мышление. Ведущая роль принадлежит математике в формировании алгоритмического мышления, воспитании умений действовать по заданному алгоритму и конструировать новые. В ходе решения задач - развиваются творческая и прикладная стороны мышления.

Основная идея

Курс изложен в доступном стиле, расцвечен непривычными для математической рутинной лексики оборотами. Выделяются основные этапы рассуждений с фиксацией внимания на выделенных этапах. Сочетание литературного языка с предметным языком. Программа создает условия для реализации проблемного подхода. Простейшие понятия даются сразу, остальные вводятся постепенно, с уточнениями и корректировкой. А некоторые остаются на интуитивном уровне восприятия до тех пор, пока не наступит благоприятный момент для их точного определения. Приоритетным является развивающее поле курса, реализован принцип развивающего обучения. Обучение на высоком уровне трудности, прохождение тем программы достаточно быстрым темпом; ведущая роль теоретических знаний; осмысление процесса обучения (ученик видит, как он умнеет в процессе изучения материала - это достигается проблемным обучением); развитие учащихся.

Целью изучения курса алгебры в 8 классе является изучение квадратичной функции и её свойств, моделирующей равноускоренные процессы.

Задачи

• Выработать умение выполнять тождественные преобразования рациональных выражений.

• Расширить класс функций, свойства и графики которых известны учащимся; продолжить формирование представлений о таких фундаментальных понятиях математики, какими являются понятия функции, её области определения, ограниченности. Непрерывности, наибольшего и наименьшего значений на заданном промежутке.

• Выработать умение выполнять несложные преобразования выражений, содержащих квадратный корень, изучить новую функцию .

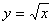• Навести определённый порядок в представлениях учащихся о действительных (рациональных и иррациональных) числах

• Выработать умение выполнять действия над степенями с любыми целыми показателями.

• Выработать умения решать квадратные уравнения и уравнения, сводящиеся к квадратным, и применять их при решении задач.

• Выработать умения решать линейные и квадратные неравенства с одной переменной; познакомиться со свойствами монотонности функции.

Особенностью курса является то, что он является продолжением курса алгебры, который базируется на функционально- графическом подходе. Это выражается в том, что какой бы класс функций, уравнений и выражений не изучался, построение материала практически всегда осуществляется по жёсткой схеме:

Функция - уравнения - преобразования.

Для оценки учебных достижений обучающихся используется:

• текущий контроль в виде проверочных работ и тестов;

• тематический контроль в виде контрольных работ;

• итоговый контроль в виде контрольной работы и теста.

2.Содержание тем учебного курса:

Повторениекурса 7 класса (4 ч.)

Числовые и алгебраические выражения. Графики функций. Линейные уравнения и системы уравнений.

Алгебраические дроби. (20 ч.)

Понятие алгебраической дроби. Основное свойство алгебраической дроби. Сокращение алгебраических дробей.

Сложение и вычитание алгебраических дробей.

Умножение и деление алгебраических дробей. Возведение алгебраической дроби в степень.

Рациональное выражение. Рациональное уравнение. Решение рациональных уравнений (первые представления).

Степень с отрицательным целым показателем.

Функция . Свойства квадратного корня. (17 ч.)

Рациональные числа. Понятие квадратного корня из неотрицательного числа. Иррациональные числа. Множество действительных чисел.

Функция , её свойства и график. Выпуклость функции. Область значений функции.

Свойства квадратных корней. Преобразование выражений, содержащих операцию извлечения квадратного корня. Освобождение от иррациональности в знаменателе дроби модуль действительного числа. График функции . Формула .

Квадратичная функция. Функция . (16 ч.)

Функция , её график, свойства.

Функция , её свойства, график. Гипербола. Асимптота.

Построение графиков функций , , , по известному графику функции .

Квадратный трёхчлен. Квадратичная функция, её свойства и график. Понятие ограниченной функции. Построение и чтение графиков кусочных функций, составленных из функций, , , , , .

Графическое решение квадратных уравнений.

Квадратные уравнения. (20 ч.)

Квадратное уравнение. Приведённое (неприведённое) квадратное уравнение. Полное (неполное) квадратное уравнение. Корень квадратного уравнения. Решение квадратного уравнения методом разложения на множители, методом выделения полного квадрата.

Дискриминант. Формулы корней квадратного уравнения. Параметр. Уравнение с параметром (начальные представления).

Алгоритм решения рационального уравнения. Биквадратное уравнение. Метод введения новой переменной.

Рациональные уравнения как математические модели реальных ситуаций.

Частные случаи формулы корней квадратного уравнения.

Теорема Виета. Разложение квадратного трёхчлена на линейные множители.

Иррациональное уравнение. Метод возведения в квадрат.

Неравенства. (15 ч.)

Свойства числовых неравенств.

Неравенство с переменной. Решение неравенств с переменной. Линейное неравенство. Равносильные неравенства. Равносильное преобразование неравенства.

Квадратное неравенство. Алгоритм решения квадратного неравенства.

Возрастающая функция. Убывающая функция. Исследование функций на монотонность (с использованием свойств числовых неравенств).

Приближённые значения действительных чисел, погрешность приближения, приближение по недостатку и избытку. Стандартный вид числа.

Обобщающее повторение. (10 ч)

3. Учебно-тематический план

Занятий по курсу «алгебра» в 8б классе

Повторение (4 часа).

Числовые и алгебраические выражения.

1

Графики функций.

1

Линейные уравнения и системы уравнений.

1

Обобщающий урок.

1

Входная работа

Глава I. Алгебраические дроби.(20 часов)

Основное свойство алгебраической дроби

3

С.р.

Сложение и вычитание алгебраических дробей с одинаковыми знаменателями

7

С.р.-2

К.р.№1

Умножение и деление алгебраических дробей. Возведение алгебраической дроби в степень.

2

Преобразование рациональных выражений.

3

С.р.

Решение рациональных уравнений.

2

Степень с отрицательным показателем.

3

С.р.

К.р.№2

Глава II. Функция. Свойства квадратного корня

(17 часов).

Рациональные числа

1

Понятие квадратного корня из неотрицательного числа.

2

Иррациональные числа

1

Множество действительных чисел

1

Функция . Её свойства и график.

3

О.с.р.

Свойства квадратных корней.

2

Преобразование выражений, содержащих операцию извлечения квадратного корня.

4

С.р.

К.р.№3

Модуль действительного числа. Изучение нового

3

Д.к.р.

Глава III. Квадратичная функция. Функция . (16 часов)

Функция у= kx², её свойства и график.

3

Функция , её свойства и график.

3

С.р.

К.р. №4

Как построить график функции y=f(x+l), если известен график функции y=f(x).

1

Как построить график функции y=f(x)+m, если известен график функции y=f(x).

1

Как построить график функции y=f(x+l)+m, если известен график функции y=f(x).

2

О.с.р.

Функция y = ax²+bx+c , её свойства и график.

2

Графическое решение квадратных уравнений.

4

С.р.

К.р.№5

Глава IV. Квадратные уравнения. (20 часов)

.

Основные понятия квадратного уравнения.

2

Формулы корней квадратного уравнения.

3

С.р.

Рациональные уравнения.

3

С.р.

К.р.№6

Рациональные уравнения как математические модели реальных ситуаций.

3

О.с.р.

С.р.

Еще одна формула корней квадратного уравнения.

2

Теорема Виета.

2

Иррациональные уравнения.

5

О.с.р.

С.р.

К.р.№7

Глава VI. Неравенства. (15 часов)

Свойства числовых неравенств. Введение темы

3

С.р.

Исследование функций на монотонность.

3

С.р.

Решение линейных неравенств.

6

С.р.

К.р. №8

Приближённые значение действительного числа

2

Стандартный вид положительного числа

1

С.р.

Итоговое повторение 10 ч

10

С.р.-2

Итоговая к.р.

ИТОГО

102 часа

К.Р.-9

С.Р.-23

4.Требования к уровню подготовки учащихся:

В результате изучения данного курса учащиеся должны уметь:

• Выполнять основные действия со степенями с целыми показателями, с многочленами и с алгебраическими дробями; выполнять разложение многочленов на множители; выполнять тождественные преобразования рациональных выражений;

• Применять свойства арифметических квадратных корней для вычисления значений и преобразований числовых выражений, содержащих квадратные корни;

• Решать квадратные уравнения и рациональные уравнения, сводящиеся к ним; решать несложные иррациональные уравнения;

• Решать линейные и квадратные неравенства с одной переменной;

• решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи;

• находить значения функции, заданной формулой, таблицей, графиком по ее аргументу; находить значение аргумента по значению функции, заданной графиком или таблицей;

• определять свойства функции по её графику; применять графические представления при решении уравнений, неравенств;

• описывать свойства изученных функций, строить их графики;

Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

• выполнения расчетов по формулам, для составления формул, выражающих зависимости между реальными величинами; для нахождения нужной формулы в справочных материалах;

• моделирования практических ситуаций и исследовании построенных моделей с использованием аппарата алгебры;

• описания зависимостей между физическими величинами соответствующими формулами, при исследовании несложных практических ситуаций;

• интерпретации графиков реальных зависимостей между величинами.

5.Литература и оборудование:

Организация учебного процесса предполагает наличие минимального набора учебного оборудования, как для демонстрационных целей в классе, так и для индивидуального использования.

Минимальный набор демонстрационного учебного оборудования включает:

• демонстрационные плакаты, содержащие основные математические формулы, соотношения, законы, таблицы метрических мер, графики основных функций;

• классные линейки, угольники, транспортир, циркуль;

• мультимедийный проектор, компьютер.

• разработанные презентации по отдельным темам.

• карточки, раздаточный материал

В наборах для индивидуального использования имеется: линейка, угольник, транспортир, циркуль.

Литература:

• Государственный стандарт основного общего образования по математике.

• Программы. Математика. 5-11 классы / авт.-сост. И.И. Зубарева, А.Г. Мордкович. - М. Мнемозина, 2011

• А.Г. Мордкович. Алгебра. 7-9кл.: Методическое пособие для учителя. - М.: Мнемозина, 2011

• Мордкович А.Г. Алгебра. 8 кл.: В двух частях. Ч.1: Учебник для общеобразоват. учреждений. - 16-е изд. -М.: Мнемозина, 2013. - 215 с.: ил.

• Мордкович А.Г. и др. Алгебра. 8 кл.: В двух частях. Ч.2: Задачник для общеобразоват. Учреждений/А.Г.Мордкович, Т.Н.Мишустина, Е.Е. Тульчинчкая. -16-е изд.,доп. -М.: Мнемозина, 2013. - 280 с.: ил

• А.Г. Мордкович, Е.Е. Тульчинская. Тесты по алгебре для 7-9 классов. - М.: Мнемозина, 2011

• Ю. П. Дудницын, Е.Е. Тульчинская. Алгебра. 7-9кл. : Контрольные работы - М.:

Мнемозина, 2011

• Л.А. Александрова. Алгебра.8 класс. Самостоятельные работы для учащихся общеобразовательных учреждений.- М: «Мнемозина», 2011

Дополнительная:

• Математика. Еженедельное учебно-методическое приложение к газете «Первое сентября».

• Л.Ф. Пичурин. За страницами учебника алгебры. - М.,1990г.

• Математика в школе. Научно-теоретический и методический журнал.

7