Рабочая программа по внеурочной деятельности «За страницами уроков математики» для 5 класса

5. Вычислите:

</ +5 +9 -5 -9

а) X XV, б) XXII , в) XIX , г) L .

6. Угадайте закономерность и заполните пропуски:

а) II, IV, VI, … , X, …, … .

б) I, III, V, …, IX, …, … .

в) V, X, …, XX, …, … .

г) III, VI, XII, …, XLVIII, … .

ЗАНЯТИЕ № 8. «Роль Л.Эйлера в развитии математики. Круги Эйлера»

1. Из 52 школьников 23 собирают значки, 36 - марки, 16 - и значки и марки. Остальные ученики не увлекаются коллекционированием. Сколько школьников не увлекаются коллекционированием?

2. В классе 15 мальчиков. Из них 10 занимаются волейболом, а 9 - баскетболом. Сколько мальчиков занимаются и волейболом, и баскетболом?.

3. В классе 35 учеников; 20 из них занимаются в математическом кружке, 11 - в биологическом, а 10 ничем не занимаются. Сколько ребят занимаются и математикой, и биологией?

4. Из 40 учащихся нашего класса 32 любят молоко, 21 - лимонад, а 15 - и молоко, и лимонад. Сколько ребят в нашем классе не любят ни молоко, ни лимонад?

5. Из 100 человек 85 знают английский язык, 80 - испанский, 75 - немецкий. Сколько человек заведомо знают все три языка?

6. 12 моих одноклассников любят читать детективы, 18 - фантастику, трое с удовольствием читают и то и другое, а один вообще ничего не читает. Сколько учеников в нашем классе?

7. Недавно мы с одноклассниками ходили на пикник. 12 человек привезли с собой бутерброды с колбасой, 5 - с сыром и 9 - с маслом. Трое сделали бутерброды двух видов: и с колбасой, и с маслом, а я захватил с собой бутерброды с маслом и сыром. Но не оказалось ни одного ученика, который привёз бы бутерброды с колбасой и с сыром. Сколько учеников было в нашей компании?

ЗАНЯТИЕ № 11. «Числа. Чётность и нечётность»

1. Ученик вычислил пример, но забыл расставить скобки. Где в этом выражении они должны стоять?

6 ∙ 8 + 20 : 4 - 2 = 58.

2. Из четырёх двоек составьте выражения, значения которых равнялись бы данным числам: 0, 1, 2, 3, 4, 6, 8, 10.

3. Числовые ребусы.

а) 95 б) УДАР

** УДАР

*5 ДРАКА

1**

****

4. Можно заплатить за товар без сдачи:

а) 20 р. семью монетами достоинством 1, 5 и 10р.;

б) 20р. семью монетами достоинством 1 и 5р.;

в) 25р. восемью монетами достоинством 1 и 5р.

5. Фокус.

Если в одной руке кто - нибудь спрячет пятирублёвую монету, а в другой - десятирублёвую монету, то я могу легко определить, в какой руке спрятана десятирублёвая монета. Для этого я попрошу умножить число рублей в правой руке на 4, в левой - на 5, результаты сложить, а мне сообщить лишь, является ли сумма чётной или нечётной. Если полученная сумма чётная, то десятирублёвая монета в левой руке, если нечётная, то в правой. Разгадайте секрет фокуса.

6. На плоскости расположены 11 шестерёнок, соединённых по цепочке. Могут ли шестерёнки вращаться одновременно?

7. Можно ли доску размером 5 * 5 заполнить косточками домино размером 1 * 2 ?

8. Все косточки домино выложили в цепь. На одном конце оказалось 5 очков. Сколько очков на другом конце?

ЗАНЯТИЕ № 12. «Интересные свойства чисел»

1. Выберите числа, которые делятся на 4: 720; 3221; 544; 7002; 334; 2080. Сформулируйте признак делимости на 4.

2. Признак делимости на 7.

Чтобы узнать, делится ли число на 7, необходимо от этого числа без трёх последних цифр отнять число из трёх последних цифр. Если эта разность делится на 7, то и число делится на 7.

Например, 348285 : 7

348 - 285 = 63.

3. Из чисел 873 656; 4436; 234 122; 3200; 567 123 выберите те, которые делятся на 7; на 4; на 7 и на 4.

4. Присмотритесь к отдельным столбцам чисел:

1 ∙ 9 = 09 90 = 9 ∙ 10

2 ∙ 9 = 18 81 = 9 ∙ 9

3 ∙ 9 = 27 72 = 9 ∙ 8

4 ∙ 9 = 36 63 = 9 ∙ 7

5 ∙ 9 = 45 54 = 9 ∙ 6

Выделенные числа являются зеркальным отражением соседних.

Рассмотрим примеры:

12 345 679 ∙ 9 = 1 111 111 111

12 345 679 ∙ 18 = 2 222 222 222

12 345 679 ∙ 27 = 3 333 333 333

12 345 679 ∙ 36 = 4 444 444 444

12 345 679 ∙ 45 = 5 555 555 555

12 345 679 ∙ 54 = 6 666 666 666

5. Умножив одно и то же число 142 857 на 2, 3, 4, 5 и 6 вы получите произведения, в которых легко заметите одну интересную особенность. В чём состоит эта особенность?

142 857 ∙ 2 = 285 714

142 857 ∙ ∙3 = 428 571

142 857 ∙ 4 = 571 428

142 857 ∙ 5 = 714 285

142 857 ∙ 6 = 857 142

6. а) Запишите максимальное число из трёх троек;

б) запишите максимальное число из трёх четвёрок без использовании математических знаков;

в) запишите максимальное число из трёх единиц без использовании математических знаков;

г) запишите максимальное число из четырёх единиц без использовании математических знаков;

д) запишите максимальное число из трёх цифр без использовании математических знаков.

ЗАНЯТИЕ № 12. «Числовые неравенства»

1. Яблоко тяжелее банана, а банан тяжелее киви. Что тяжелее: киви или яблоко?

2. Мандарин легче груши, а апельсин тяжелее мандарина. Что тяжелее: груша или апельсин?

3. Один сапфир и два топаза

ценней, чем изумруд, в три раза,

А семь сапфиров и топаз

его ценнее в восемь раз.

Определить мы просим вас,

сапфир ценнее иль топаз?

4. Стоимость 7 одинаковых книг не превышает 12 рублей, а 10 таких книг стоят 17 рублей и несколько копеек.

найдите стоимость одной книги.

5. Известно, что 9 стаканов чая стоят дешевле 10р., а 10 стаканов чая - дороже 11р. Сколько стоит стакан чая?

ЗАНЯТИЕ № 14. «Делимость и остатки»

1. Найдите последнюю цифру числа 100! = 1 ∙ 2 ∙ 3 ∙ …. ∙ 100.

2. Какова последняя цифра числа 3 542 645 ∙ 345 603 + 56 404 ∙ 4 398 718?

3. Числа 100 и 90 разделили на одно и то же число. В первом случае в остатке получили 4, во втором - 18. Назовите делитель.

4. Маша начала считать свои пальцы от большого к мизинцу. Досчитав до пяти, она продолжила счёт в обратном направлении. Таким способом Маша досчитала до числа 2003, при этом большой палец стал девятым. На каком пальце она остановилась?

5. Докажите, что среди произвольных 25 целых чисел существует два числа, разность которых делится на 24.

6. Найдите наименьшее натуральное число, которое даёт остаток 1 при делении на любое из чисел 2, 4, 6, 8.

ЗАНЯТИЕ № 16. «Задачи на взвешивание»

1. У хозяйки есть рычажные весы и гиря в 100 г. Как за 3 взвешивания она может отмерить 700 г. крупы?

2. На одной чашке весов лежат 6 одинаковых яблок и 3 одинаковые груши, на другой чашке - 3 таких же яблока и 5 таких же груш. Весы находятся в равновесии. Что легче яблоко или груша?

3. Из 9 монет одна фальшивая - она легче остальных. Как за два взвешивания на чашечных весах без гирь определить фальшивую монету?

4. Есть 27 монет. Известно, что одна из них фальшивая (она тяжелее настоящих). Как за три взвешивания на чашечных весах без гирь определить фальшивую монету?

5. В корзине лежат 13 яблок. Имеются весы, с помощью которых можно узнать общую массу любых двух яблок. Придумайте способ выяснить за 8 взвешиваний общую массу всех яблок.

6. Имеются чашечные весы без гирь и 4 одинаковые по внешнему виду монеты. Одна из монет фальшивая, причём неизвестно, легче она настоящих или тяжелее (настоящие монеты одной массы). Сколько надо сделать взвешиваний, чтобы найти фальшивую монету?

7. Известно, что среди ста монет имеется одна фальшивая. с помощью двух взвешиваний на чашечных весах без гирь определите, легче или тяжелее фальшивая монета по сравнению с настоящей.

ЗАНЯТИЕ № 17. «Задачи на переливание»

1. Имеются два сосуда вместимостью 3 л и 5 л. Как с помощью этих сосудов налить 4 л воды?

2. Имеются два сосуда вместимостью 8 л и 5 л. Как с помощью этих сосудов налить 7 л воды?

3. Однажды Винни - Пух захотел полакомиться мёдом и пошёл к пчёлам в гости. По дороге нарвал букет цветов, чтобы подарить труженицам - пчёлкам. Пчёлки очень обрадовались, увидив мишку с букетом цветов и сказали: «У нас есть большая бочка с мёдом. Мы дадим тебе мёда, если ты сможешь с помощью трёхлитровой банки и сосуда вместимостью 7 л налить себе 5 л». Винни - Пух долго думал, но всё - таки смог решить эту задачу. Как он это сделал?

4. В шестилитровом ведре содержится 4 л кваса, а в семилитровом - 6 литров. Разделите квас пополам, пользуясь этими вёдрами и пустой трёхлитровой банкой.

5. Имеются 2 типа песочных часов. Одни отмеряют 7 мин, а другие - 11 минут. Как с их помощью отмерить 15 мин?

6. Можно ли отмерить 15 литров воды, находясь у реки и имея два ведра: одно вместимостью 11 литров, другое - вместимостью 7 литров?

7. Можно ли разлить 50 л бензина в три бака так, чтобы в первом баке было на 10 л больше, чем во втором, а после переливания 26 л из первого бака в третий в третьем баке стало столько же бензина, сколько во втором?

8. Есть три бидона ёмкостью 14 л, 9 л, 5 л. В большем бидоне 14 л молока, остальные бидоны пусты. Как с помощью этих сосудов разделить молоко пополам?

ЗАНЯТИЕ № 18. «Задачи на разрезание»

1. Начертите прямоугольник размером 4 ˟ 6 клеток. Покажите, как его замостить трёхклеточными уголками так, чтобы никакие два из них не образовывали прямоугольник. (Замостить - покрыть без образования наложений и свободных клеток).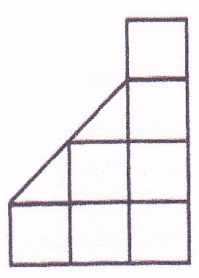

2. Разрежьте прямоугольник 3 ˟ 9 на восемь квадратов.

3. Фермер оставил двум сыновьям в наследство участок земли, имеющий форму фигуры, изображённый на рисунке 1. Как его разделить на два равных по форме и размеру участка?

рис. 1

4. Незнайка разрезал фигуру (рис. 2) на уголки и трёх и четырёх клеток. Сколько трёхклеточных уголков могло получиться?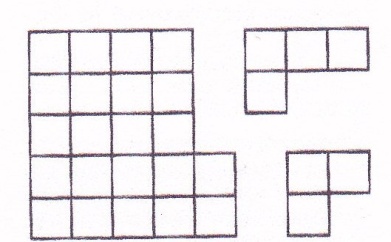

рис. 2

ЗАНЯТИЕ № 19. «Задачи со спичками».

1. 12 спичек выложены так, как показано на рисунке 3. Сколько получилось квадратов?

а) Уберите две спички так, чтобы образовалось 2 неравных квадрата.

б) Переложите 3 спички так, чтобы образовалось 3 равных квадрата.

в) Переложите 4 спички так, чтобы образовалось 10 квадратов.

рис.3

2. Сложите из 6 одинаковых спичек геометрическую фигуру, состоящую из 4 равных треугольников. Спички при этом ломать нельзя.

3. Как из двух спичек сделать пять?

4. Как с помощью трёх спичек получить три равных квадрата?

Как с помощью трёх спичек получить четыре равных квадрата?

5. На рисунке 4 переложите 3 спички так, чтобы стрела поменяла своё направление на противоположное.

рис.4

6. Из спичек составлено неверное равенство (рис. 5). Переставьте одну спичку так, чтобы равенство было верным.

рис.5

7. В трёх кучках лежат спички, по 10 спичек в каждой. Играют Аня и Вова. Ход состоит в том, что игрок забирает несколько спичек из одной кучки. Игру начинает Аня. Побеждает тот, кому достанется последняя спичка. Может ли кто - нибудь из игроков играть так, чтобы наверняка выиграть, как бы ни старался другой?

8. Расположите 6 спичек так, чтобы получилось 4 треугольника.

ЗАНЯТИЕ № 20. «Составление выражений»

1. Между цифрами 1 2 3 4 5 6 7 8 9 расставьте знаки арифметических действий и скобки так, чтобы получилось выражение, равное 100.

2. Как нужно расставить скобки, чтобы получилось верное равенство?

а) 3248 : 16 - 3 ∙ 315 - 156 ∙ 2 = 600;

б) 350 - 15 ∙ 104 - 1428 : 14 = 320.

3. По какому правилу записаны числа? Запишите следующие 2 числа: 2 7 4 9 6 11 8.

4. Цифрами 0, 1, 2, 3 запишите наибольшее и наименьшее шестизначное число. Каждую цифру нужно использовать не менее одного раза.

5. Запишите в строчку три числа так, чтобы сумма любых двух соседних чисел была чётная, а сумма всех чисел - нечётная.

6. К числу 10 припишите слева и справа по одной цифре так, чтобы получившееся число делилось на 72.

7. В записи 52*2* замените * цифрами так, чтобы полученное число делилось на 36. Укажите все возможные решения.

8. Из карточек сложили неверное равенство (рис. 6):

Как, передвинув лишь одну карточку, сделать его верным?

рис.6

ЗАНЯТИЕ № 21. «Путь и движение»

1. Два поезда вышли навстречу друг другу из двух городов, расстояние между которыми 782 км. Скорость первого поезда 52 км/ч, а второго - 61 км/ч. Пройдя 416 км, первый поезд встретился со вторым. На сколько один из поездов вышел раньше второго?

2. Моторная лодка плыла 3 ч по озеру. Пройденный путь составил 96 км. Найдите собственную скорость лодки, если скорость течения реки 2 км/ч.

3. Два человека бегут по ступенькам эскалатора метро (эскалатор и люди двигаются в одном направлении). Один бежит быстрее другого. Кто насчитает больше ступенек?

4. Крестьянину нужно переправить через реку волка, козу и капусту. Но лодка такова. что в ней может поместиться только крестьянин, а с ним - или только волк, или только коза, или только капуста. Но если оставить волка с козой без крестьянина, то волк съст козу, а если оставить козу с капустой, то коза съст капусту. Как быть?

5. Если Серёжа поедет в школу автобусом, а обратно пешком, то он затратит на весь путь 1 ч 30 мин. Если же в оба конца он поедет на автобусе, то затратит всего 30 мин. Сколько времени потратит Серёжа на дорогу если он пойдёт пешком и в школу. и обратно?

6. Собака. находясь в точке А, погналась за лисицей, которая была на расстоянии 30 м от собаки. Прыжок собаки равен 2 м, а прыжок лисицы - 1 м. Собака делает два прыжка в то время, когда лисица делает три прыжка. На каком расстоянии от точки А собака догонит лисицу?

7. От потолка комнаты вертикально вниз по стене ползли две мухи. спустившись до пола, они поползли обратно. Первая муха ползла в оба конца с одной и той же скоростью, а вторая хотя и поднималась двое медленнее первой, но зато спускалась вдвое быстрее. Какая из мух раньше приползёт обратно?

8. Поезд проходит мост длиной 250 м за 1ё минуту, а мимо телеграфного столба проходит за полминуты. Какова длина моста?

ЗАНЯТИЕ № 22. «Логические задачи»

1. Встретились три подруги6 Белова, Краснова, Чернова. На одной из них было чёрное платье, на другой - красное, на третьей - белое. Девочка в белом платье говорит Черновой: «Нам надо поменяться платьями. а то цвет наших платьев не соответствует фамилиям». кто в каком платье был одет?

2. Коля. Вова, Боря и Юра заняли первые места в соревновании. На вопрос, какое место они заняли, трое из них ответили:

1) Коля ни первое, ни четвёртое;

2) Боря - второе;

3) Вова не был последним.

Какое место занял каждый мальчик?

3. Три друга: Коля, Олег и Петя - играли во дворе, и один из них случайно разбил стекло мячом. Коля сказал: «Это не я разбил стекло». Олег сказал: «Это Петя разбил». Позднее выяснилось, что одно из этих утверждений верное, а другое - нет. Кто из мальчиков разбил стекло?

4. Митя, Толя, Сеня и Костя пришли в музей и встали в очередь. Если бы Митя встал посередине очереди, то он оказался бы между сеней и Костей, а если бы Митя встал в конце очереди, то рядом с ним мог бы быть Юра, но Митя встал впереди всех своих товарищей. Кто за кем стоит?

5. На столе лежат четыре фигуры: треугольник, ромб, квадрат и круг. Цвета этих фигур - зелёный, жёлтый, синий, красный. В каком порядке лежат фигуры и каков цвет каждой из них, если:

• фигура красного цвета лежит между зелёной и синий;

• справа от жёлтой фигуры лежит ромб;

• круг лежит не с краю;

• и, наконец, фигура синего цвета не лежит рядом с фигурой жёлтого цвета?

6. Клоуны Бам, Бим и Бом вышли на арену в красной, синей и зелёной рубашках. Их туфли тоже были тех же разных цветов. Туфли и рубашка Бима были одного цвета. На Боме не было ничего красного. Туфли Бама были зелёными, а рубашка - нет. Каких цветов были туфли и рубашки у Бома и Бима?

7. У мальчиков столько же сестёр, сколько братьев, а у его сестры вдвое меньше сестёр, чем братьев. Сколько в этой семье сестёр и сколько братьев?

8. На острове живут рыцари, которые всегда говорят правду, и лжецы, которые всегда лгут. Каждый из собравшихся на площади жителей заявил остальным: «Все вы - лжецы». Сколько рыцарей среди них?

ЗАНЯТИЕ № 23. «Принцип Дирихле»

1. В школе учатся 370 человек. Докажите, что среди всех учащихся найдутся 2 человека, празднующие свой день рождения в один и тот же день.

2. В классе 40 учеников. Найдётся ли такой месяц в году, в котором отмечают свой день рождения не меньше чем 4 ученика этого класса?

3. В классе 30 учеников. В диктанте Вова сделал 13 ошибок, а остальные ученики допустили ошибок меньше. Докажите, что по крайней мере три ученика сделали ошибок поровну.

4. В магазин привезли 25 ящиков с яблоками трёх сортов, причём в каждом ящике лежат яблоки какого - то одного сорта. Можно ли найти 9 ящиков с яблоками одного сорта?

5. В ящике лежат цветные карандаши: 10 красных, 8 синих и 4 жёлтых. В темноте берём из ящика карандаши. какое наименьшее число карандашей надо взять, чтобы среди них заведомо было:

а) не менее 4 карандашей одного цвета;

б) не менее 6 карандашей одного цвета;

в) хотя бы один карандаш каждого цвета;

г) не менее 6 синих карандашей.

6. Пять мальчиков собрали 14 грибов, каждый нашёл хотя бы один гриб. Докажите, что хотя бы два мальчика нашли одинаковое число грибов.

ЗАНЯТИЕ № 24. «Комбинаторные задачи»

1. Сколько различных чисел можно получит, переставляя цифры чисел:

а) 133: б) 9854; в) 3213; г) 98 561?

2. На почте продают 5 видов конвертов и 4 вида марок. Сколькими способами можно купить конверт и марку?

3. В футбольной команде 911 человек) нужно выбрать капитана и его заместителя. сколькими способами это можно сделать?

4. Сколько существует трёхзначных чисел, в запись которого входит ровно одна цифра 5?

5. Имеется пять одинаковых стульев и обивочная ткани трёх разных цветов. Сколько существует вариантов обивки всех стульев, если каждый стул можно обить тканью любого цвета?

6. Сколько существует девятизначных чисел, цифры которых расположены в порядке убывания (то есть каждая следующая меньше предыдущей)?

7. Начальник транспортного цеха пригласил несколько человек на совещание. Каждый участник совещания, входя в кабинет, пожимал руки всем присутствующим. сколько человек участвовали в совещании, если было всего 78 рукопожатий7

ЗАНЯТИЕ № 25. «Задачи на уравнивание»

1. С двух яблонь собрали 67 кг яблок, причём с одной из них собрали на 19 кг больше, чем с другой. Сколько килограмм яблок собрали с каждой из яблонь?

2. На трёх полках лежат 44 книги. на первой - на 3 книги больше. чем на второй, а на третьей - на 8 книг больше, чем на первой. Сколько книг лежало на каждой полке?

3. Периметр прямоугольника равен 44 см. Его длина на 6 см больше ширины. Найдите все стороны прямоугольника.

4. Два автомобиля одновременно выехали из одного пункта в противоположных направлениях. Скорость одного автомобиля на 15 км/ч больше другого. Найдите скорости каждого автомобиля, если известно, что через три часа расстояние между ними будет 330 км.

5. Масса бидона с молоком 32 кг, без молока - 2 кг. какова масса бидона, заполненного молоком наполовину?

ЗАНЯТИЕ № 26. «Задачи на части»

1. Мороженое содержит 7 частей воды, 2 части молочного жира и 2 части сахара. Сколько потребуется сахара для приготовления 2200 г мороженого?

2. Чтобы сделать клей, берут 11 частей воды, 5 частей нашатырного спирта, 4 части казеина. Сколько получиться казеиного клея, если на него будет израсходовано нашатырного спирта на 60 г. меньше, чем воды?

3. При изготовлении кофейного напитка «Ячменный» на 4 части ячменя берут 1 часть цикория. Сколько пачек напитка изготовлено, если каждая пачка весит 250 г. и на изготовление партии напитка израсходовано ячменя на 36 кг. больше, чем цикория?

4. Мальчик разрезал провод на три части так, что первая часть оказалась в 2 раза длиннее второй части, а третья часть в 4 раза больше первой. Какова длина провода, если меньшая часть на 35 см. короче большей?

5. За три часа велосипедист проехал 36 км. За 1 час он проехал в 2 раза больше, чем во второй час, а в третий - в 3 раза больше, чем в первый. Сколько километров проезжал велосипедист за каждый час?

6. Дочери в настоящее время 8 лет, а матери - 38 лет. Через сколько лет мать будет втрое старше дочери?

ЗАНЯТИЕ № 27. «Старинные русские занимательные задачи»

1. Лодочник, плывя против течения, уронил под мостом шляпу. Через час он обнаружил пропажу, погнался за шляпой и догнал её в 4 км от моста. какова скорость течения реки?

2. Двое мальчиков катались на лодке. к берегу подошёл отряд солдат. Лодка мала, что на ней могли переправиться двое мальчиков или только один солдат. Смогли ли солдаты переправиться через реку?

3. Женщина несла на продажу корзину яиц. Встретившийся прохожий по неосторожности так толкнул её, что корзина упала на землю и все яйца разбились. Прохожий захотел заплатить женщине стоимость разбитых яиц и спросил, сколько их всего было. «Я не помню этого, = сказала женщина, - знаю только хорошо, что когда я перекладывала яйца по 2, то оставалось одно яйцо. Точно так же всегда оставалось по одному яйцу, когда я перекладывала по 3, по 4, по 5 и по 6. Когда же я перекладывала их по 7, то не оставалось ни одного яйца».

Спрашивается, сколько было яиц?

4. Пруд зарастает лилиями, причём за неделю площадь, занятая лилиями, удваивается. За сколько недель пруд покрылся лилиями наполовину, если полностью он покрывается лилиями за 8 недель?

5. Старик, имевший трёх сыновей, распорядился, чтобы они после его смерти поделили принадлежащее ему стадо верблюдов так, чтобы старший взял половину всех верблюдов, средний - треть и младший - девятую часть всех верблюдов. Старик умер и оставил 17 верблюдов. Сыновья начали делёж, но оказалось, что число 17 не делится ни на 2, ни на 3, ни на 9. В недоумении, как им быть, братья обратились к мудрецу. Тот приехал к ним на собственном верблюде и разделил по завещанию. Как он это сделал?

ЗАНЯТИЕ № 29. «Части и проценты»

1. В школе 800 учащихся. Из них 46% приняли участие в математической олимпиаде. Сколько человек приняли участие в олимпиаде?

2. Товар стоил 10000 рублей. Продавец поднял цену на 10%, а через месяц снизил её на 10%. Сколько стал стоить товар после этого снижения?

3. В городе N живёт 44100 человек. Известно, что каждые три года население увеличивалось на 5%. Сколько жителей было в городе N два года назад?

4. В двух бочках было воды поровну. В первой бочке количество воды сначала увеличилось на 10%, а затем уменьшилось на 10%. Во второй вначале уменьшилось на 10%, а затем увеличилось на 10%. В какой бочке воды сало больше?

5. Цену товара уменьшили на 10%, а затем ещё на 10%. Стоит ли товар дешевле, если его цену сразу снизить на 20%?

6. Содержание сахара в одном соке - 10%, а в другом - 15%. смешали 2 л первого и 3 л второго соков. Каково содержание сахара в смеси?

ЗАНЯТИЕ № 30. «Головоломки и числовые ребусы»

1. Вася записывает последовательность чисел, так что каждое следующее число определяется по некоторому правилу. Определите это правило для каждого ряда чисел и запишите следующее число.

а) 3; 13; 23; 33; …

б) 1; 2; 3; 5; 8; …

в) 1; 1; 2; 3; 5; …

г) 11; 101; 1001; 10001; …

д) 2; 5; 11; 23; 47; …

2. Решите ребусы.

а) УРАН б) ТУЗИК

УРАН ТУЗИК

НАУКА КАРТУЗ

3. Магические квадраты. Расставьте в квадрате числа 1, 2. … , 9 так, чтобы сумма цифр в каждой строке, столбце и по диагонали была одинаковой.

4. У вас имеется 16 одинаковых квадратов четырёх цветов - по 4 квадрата каждого цвета. сложите из них квадрат 4 ˟ 4 так, чтобы одинаковые цвета не повторялись ни в строчках, ни в столбцах.

5. Выписали все натуральные числа от 1 до 99 без промежутков. Получилось огромное число:

12345678910111213141516171819202122 … 9596979899

а) Сколько раз в записи этого числа встречается цифра 1?

б) Делится ли это число на 9?

6. Некоторое шестизначное число начинается цифрой 7. Откинув эту цифру слева и приписав её справа, получим число, в пять раз меньшее первоначального. Найдите первоначальное число.

ЗАНЯТИЕ № 33. Задания для «Соревнование. Математическая регата»

1 ТУР

1. В школе 30 классов и 1000 учеников. Докажите, что есть класс, в котором не менее 34 учеников.(2 балла)

2. Можно ли отмерить 8 литров воды, находясь у реки и имея два ведра: одно вместимостью 15 литров, другое - вместимостью 16 литров? (2 балла)

3. Найдите значение выражения (В∙А∙Р∙Е∙Н∙Ь∙Е) : (К∙А∙Р∙Л∙С∙О∙Н).(3балла)

2 ТУР

1. В магазин привезли 25 ящиков с яблоками трех сортов, причем в каждом ящике лежали яблоки одного сорта. Найдутся ли 9 ящиков одного сорта?

(2 балла)

2. Один сапфир и три топаза ценней, чем изумруд, в три раза. А семь сапфиров и топаз его ценнее в восемь раз. Определить прошу я вас,

сапфир ценнее иль топаз? (3 балла)

3. Таня пошла покупать ручки и карандаши. На все деньги, которые у нее были, она могла купить 6 ручек. На те же деньги она могла

купить 12 карандашей. Но она решила купить одинаковое количество ручек и карандашей. Сколько?(4 балла)

3 ТУР

1. В школе 400 учеников. Докажите, что хотя бы двое из них родились в один день года.(2 балла)

2. Бутылка и стакан весят столько же, сколько кувшин. Бутылка весит столько же, сколько стакан и тарелка. Два кувшина весят столько же,

сколько три тарелки. Сколько стаканов уравновешивают одну бутылку?(4 балла)

3. Используя ровно пять раз цифру 5, представьте любое число от 0 до 10.(5 баллов)

ЗАНЯТИЕ № 34. Задания для «Соревнование. Математическая карусель»

1. До царя дошла весть, что кто-то из трех богатырей убил Змея Горыныча. Приказал царь им явиться ко двору. Молвили богатыри:

Илья Муромец: Змея убил Добрыня Никитич.

Добрыня Никитич: Змея убил Алеша Попович.

Алеша Попович: Я убил Змея.

Известно, что только один богатырь сказал правду, а двое слукавили. Кто убил змея.

2. На улице, став в кружок, беседуют четыре девочки: Аня, Валя, Галя и Надя. Девочка в зеленом платье (не Аня и не Валя) стоит

между девочкой в голубом платье и Надей. Девочка в белом платье стоит между девочкой в розовом и Валей. Кто какое платье носит?

3. Из числа 382818 вычеркните две цифры так, чтобы получилось наибольшее возможное число.

4. Расставьте знаки арифметических действий и скобки, чтобы получились верные равенства: а) 4 4 4 4=5; б) 4 4 4 4=17; в) 4 4 4 4=20;

г) 4 4 4 4=32; д) 4 4 4 4=64.

5. Разделите 7 полных, 7 пустых и 7 полупустых бочек меда между тремя купцами, чтобы всем досталось поровну и бочек, и меда.

(Мед из бочки в бочку не переливать!)

6. Продолжите последовательность чисел: 1, 11, 21, 1112, 3112, 211213, 312213, 212223, 114213, …

7. Отлейте из цистерны 13 литров молока, пользуясь бидонами емкостью 17 и 5 литров.

8. Решите ребус: КНИГА + КНИГА + КНИГА = НАУКА.