Конспект урока геометрии в 8 классе 'Теорема Пифагора'

Муниципальное автономное общеобразовательное учреждение

«Средняя общеобразовательная школа №141 с углубленным изучением отдельных предметов»

Советского района города Казани РТ

Конспект урока по математике
в 8 классе
«Теорема Пифагора»

подготовила

учитель математики

высшей квалификационной категории

Бухарова Лидия Николаевна

г. Казань

2015

Список использованной литературы

1. Геометрия 7-9 под редакцией Руденко В.Н.
2. Геометрия 7-9 под редакцией Атанасян Л.С.
3. Приложение к газете «Математика» №13 за 1996год, «Поговорим о теореме Пифагора»

Тема урока: «Теорема Пифагора»

Урок№1.

Цели урока:

1. Используя исторические сведения, раскрыть смысл и содержание известнейшей теоремы геометрии - теоремы, носящей имя древнегреческого математика Пифагора.

2. Показать учащимся эстетику наглядности геометрических доказательств.

3. Научить учащихся применять теорему Пифагора в решении геометрических и алгебраических задач.

4. Показать практическое применение теоремы и теоремы, обратной теоремы Пифагора.

5. Привить интерес к предмету, показав множество доказательств теоремы и предложив принять участие в самостоятельном доказательстве по готовым рисункам.

ХОД УРОКА.

1. Теоретическая часть.

Еще в глубокой древности возникла необходимость вычислять стороны прямоугольных треугольников по двум известным сторонам. Такие задачи решаются при проектировании любых строительных объектов. Приведем пример из нашей повседневной жизни:

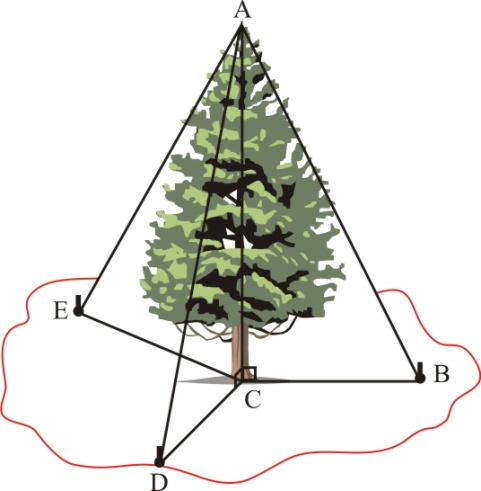
На площади устанавливается елка высотой 8м. Для закрепления ее в вертикальном положении от вершины елки делают проволочные натяжки АВ, АЕ, AD одинаковой длины и закрепляют на земле на расстоянии 6м от основания елки. Какой длины должна быть натягивающая проволока, чтобы елка занимала вертикальное положение? Эта задача решается просто с помощью теоремы Пифагора.

Теорема Пифагора:

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

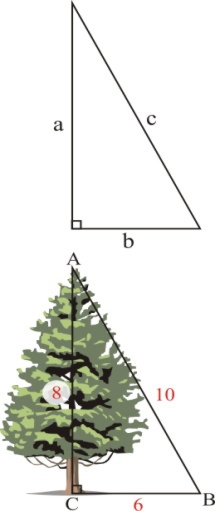
Если а и b катеты, с - гипотенуза, то

с² = а²+b²

или в нашей задаче - АС и СВ - катеты, АВ - гипотенуза, т.е. по теореме Пифагора

АВ² = АС² + СВ²

АВ² =8² + 6² =100,

Тогда АВ = √100 = 10 (м)

Мы докажем теорему чуть позже, а пока немного о Пифагоре - именем которого названа теорема.

Итак, Пифагор Самосский жил ≈ 2,5 тысячи лет тому назад. Это был знаменитый греческий философ и математик. Дошедшие до нас биографические сведения о Пифагоре отрывочны и, вероятно, далеко недостоверны. С его именем связано много легенд. Известно, что Пифагор много путешествовал по странам Востока, посещал Египет и Вавилон. В одной из греческих колоний Южной Италии им была основана знаменитая «Пифагорова школа». Именно Пифагору приписывают доказательство известной геометрической теоремы. Длительное время считалось, что до Пифагора эта теорема не была известна. Так Прокл в комментарии к «Началам» Евклида пишет:

«Если слушать тех, кто любит повторять древние легенды, то придется сказать, что эта теорема восходит к Пифагору. Рассказывают, что в честь этого открытия он принес в жертву быка»

Однако не подлежит сомнению и то, что эту теорему знали за много лет до Пифагора. Так, за 1500 лет до Пифагора древние египтяне знали о том, что треугольник со сторонами 3,4 и 5 единиц является прямоугольным и пользовались этим свойством (т. е теоремой, обратной теореме Пифагора). И сейчас сельские строители, и плотники, закладывая фундамент какой-либо постройки, вычерчивают этот треугольник, чтобы получить прямой угол. Это делали и тысячи лет при строительстве великолепных храмов в Египте, Вавилоне, Китае. Сейчас треугольник со сторонами 3,4 и 5 часто называют египетским треугольником

Таким образом, Пифагор не открыл свойство прямоугольного треугольника, он сумел обобщить и доказать его. Доподлинно известно - как именно он сумел это сделать. В настоящее время доказательств теоремы Пифагора - более и менее строгих - известно более 150. Некоторые историки математики предполагают, что доказательство Пифагора было не принципиальным, а лишь подтверждением, проверкой этого свойства на ряде частных видов треугольников, начиная с равнобедренного прямоугольного треугольника, для которого оно, очевидно, следует из следующего рисунка:

.

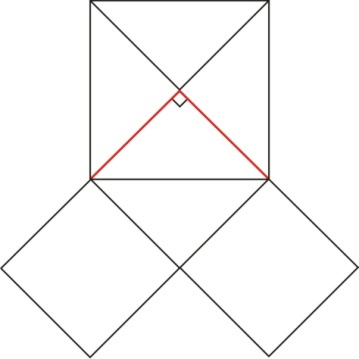
Приведем пример доказательства теоремы Пифагора, принадлежащее древним индусам; это доказательство основано на использовании понятия равновеликости фигур. Это простое и наглядное доказательство. На рисунке изображено два равных квадрата. Длина стороны каждого квадрата, а + b. Каждый квадрат разбит на части, состоящие из квадратов прямоугольных треугольников. Ясно, что если от площади квадрата отнять учетверенную площадь прямоугольного треугольника с катетами а, b, то останутся площади, равные между собой, т.е. с² = а² + b². Впрочем, древние индусы не записывали доказательство, а сопровождали только одним словом «смотри!»

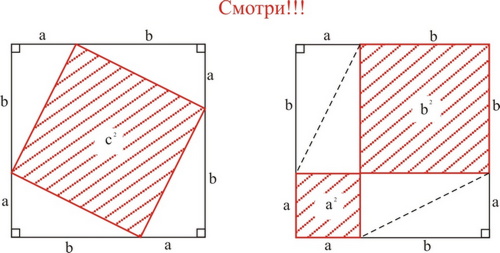
Следующий рисунок - иллюстрация доказательства великого индийского математика Бхсари (XII век). Его тоже сопровождало одно слово «смотри!»

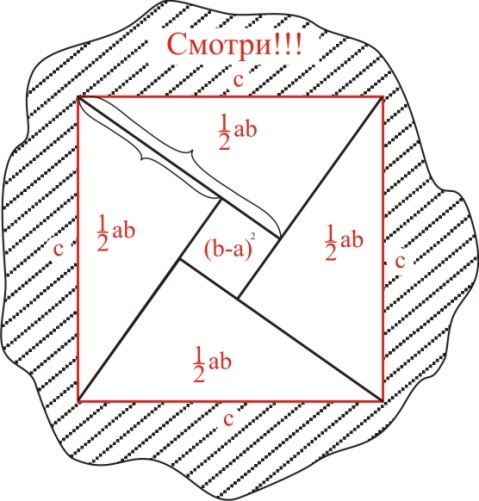
Очевидно, что:

(b-a)² + 4•½•ab = c² или

b² - 2ab + a² +2ab =c² т.е.

b² + a² = c² что и требовалось доказать.

Итак, давайте еще раз запишем и докажем теорему Пифагора.

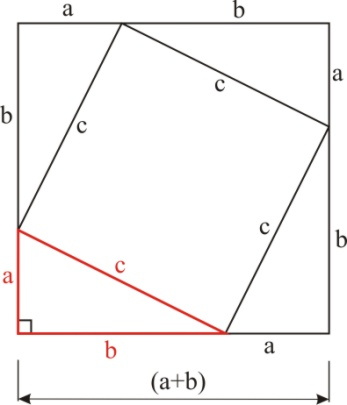
Дано: прямоугольный треугольник, а,b катеты, с - гипотенуза

Доказать: a² + b² = c²

Доказательство:

1. Достроим данный треугольник до квадрата со стороной (а + b)

2. S - Площадь получившегося квадрата равна (а + b)², т.е. S =(a +b)²

3. С другой стороны: S = ½ ab • 4 + c² , или

a² + 2ab + b² = 2ab + c ² ; a² + b² = c² ч.т.д.

2. Рассмотрим примеры:

Задача: найти неизвестный элемент прямоугольного треугольника с катетами а, b и гипотенузой с.

а) Дано: а = 3см, b = 4см. Найти: с

По теореме Пифагора с² = а² + b² = 3² + 4² = 25

с² =25, с =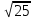 =5 (см)

или с =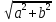 = = 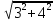=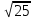5 (см)

б) Дано: а = 2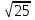 см; b = 3 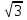см. Найти: с

с = 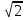= = 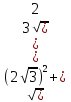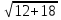(см)

в) Дано: а = 6см; с =10 см. Найти b

= -

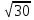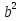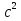
b = 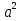= = 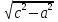= = 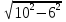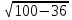8 (см)

г) Дано: b = 15дм; с = 20 дм. Найти: а

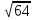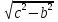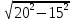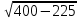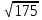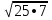а = = = = = =7 (см)

Рассмотрим теорему, обратную теореме Пифагора:

Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный.

(Доказательство рассмотрите самостоятельно в учебнике)

Пример: Докажите, что треугольник со сторонами 15, 20 и 25 см является прямоугольным

Решение: если 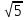= 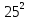+ 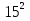, то по теореме обратной теореме Пифагора этот треугольник будет прямоугольным. Действительно

625 = 125 +400; 625=625;

Т.е. равенство 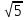= 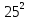+ 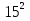верное, треугольник прямоугольный.

3. Итоги урока, домашняя работа.

Итак, мы изучили и доказали теорему Пифагора, раскрыли смысл теоремы, обратной теореме Пифагора, рассмотрели конкретные примеры, попробуйте доказать теорему самостоятельно, используя любой из готовых рисунков.

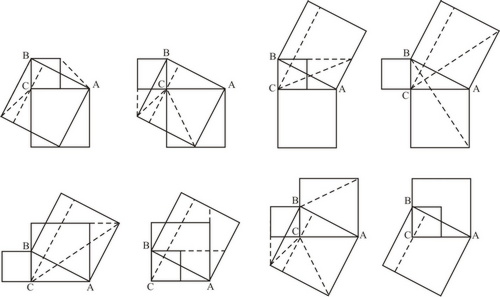
Доказательство теоремы обратной теореме Пифагора.

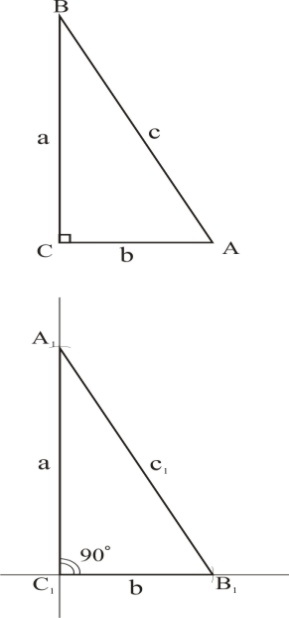
Пусть стороны ∆АВС связаны соотношением

с² = а² + b² (1)

Построим прямоугольный треугольник 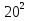по двум катетам, длины которых равны а и b катетов данного треугольника. Пусть гипотенуза построенного треугольника равна 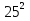. Так как построенный треугольник прямоугольный, то по теореме Пифагора имеем:

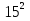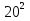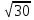= + (2)

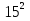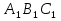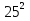Сравнивая (1) и (2) получаем, что = или = с

Таким образом, ∆АВС= ∆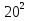, по трем сторонам, следовательно, 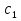=∠С как соответственные углы в равных треугольниках,

т.е. ∠С = 90°