Разработка урока по геометрии 'Практическое применение подобных треугольников' (8 класс)

Муниципальное бюджетное образовательное учреждение «Качалинская СОШ №2»

Иловлинского района Волгоградской области

Разработка урока с использованием интерактивной доски

по ГЕОМЕТРИИ для учащихся 8 класса

по теме «Практическое применение подобия треугольников»

Учитель математики

высшей категории

Постоева Жанна Васильевна

Станица Качалинская

2015 г.

Урок по теме «Практическое применение подобия треугольников» разработан для учащихся 8 класса на основе учебника «Геометрия» Л.С.Атанасяна

Тип урока: изучение нового материала.

Оборудование:

Интерактивная доска и мультимедиапроектор

Цели:

Личностные:

- формировать у учащихся умение работать самостоятельно и в группах;

- развивать логическое и критическое мышление;

- воспитывать коммуникативные качества личности, настойчивость в достижении цели.

Метапредметные:

- формировать умение переводить словесную запись задачи в символическую;

- формировать умения и навыки умственного труда - планирование своей работы, поиск рациональных путей ее выполнения, критическая оценка результатов;

- формировать умение абстрагировать условие задачи и обобщать способы решения;

- развивать умение в применении знаний в конкретной ситуации;

- развивать логическое мышления, умение сравнивать, обобщать, правильно формулировать задачи и излагать мысли.

Цели:

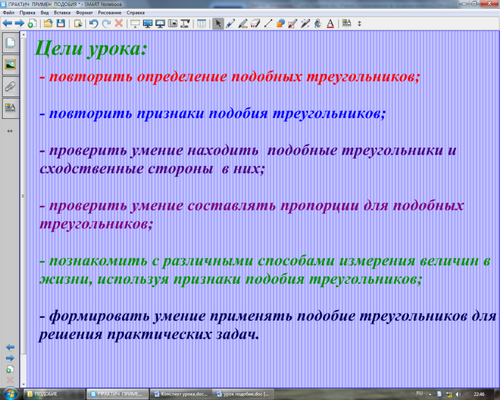
предметные:

- повторить определение подобных треугольников;

- повторить признаки подобия треугольников;

- проверить умение находить подобные треугольники и сходственные стороны в них;

- проверить умение составлять пропорции для подобных треугольников;

- познакомить с различными способами измерения величин в жизни, используя признаки подобия треугольников;

- формировать умение применять подобие треугольников для решения практических задач.

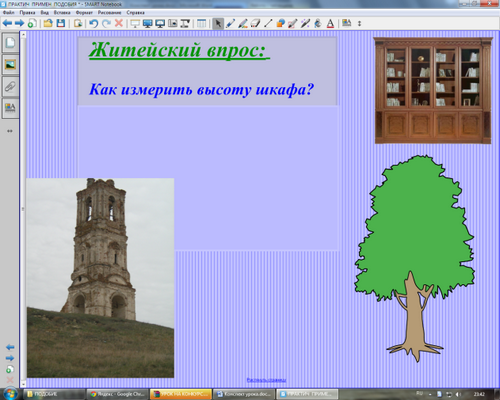
Учитель: Приветствие. Хочу начать урок с житейского вопроса:

Как измерить высоту шкафа? (с помощью линейки или метра)

А как измерить высоту дерева?

Или как измерить высоту нашей колокольни? (выслушать предлагаемые варианты)

Учитель:

Подобные вопросы возникали и у людей в давние времена. И они могли справляться с такими задачами. Как? Сегодня и вы сможете ответить на эти вопросы.

А для начала давайте повторим материал, пройденный на прошлых уроках.

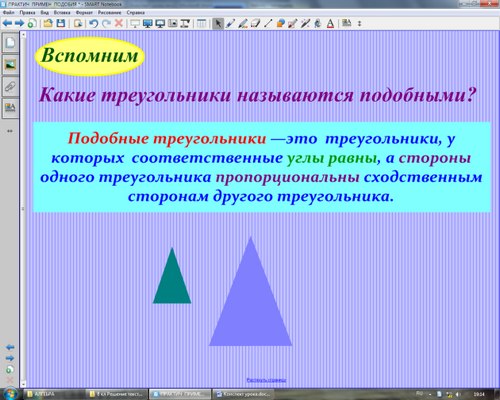
Какие треугольники называются подобными?

(После ответа учащихся учитель показывает определение.)

Учитель: Назовите признаки подобия треугольников.

(После ответов учащихся учитель показывает признаки подобия треугольников в краткой записи)

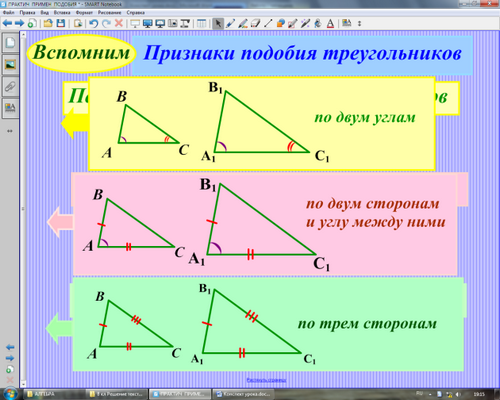
(Для решения задач необходимо уметь находить подобные треугольники, сходственные стороны в них и составлять пропорции. Для этой цели учащимся предлагаются следующие задачи.)

(Первую задачу учащиеся решают устно.)

Учитель: Назовите подобные треугольники (признак), сходственные стороны этих треугольников, составьте пропорцию, найдите неизвестные величины.

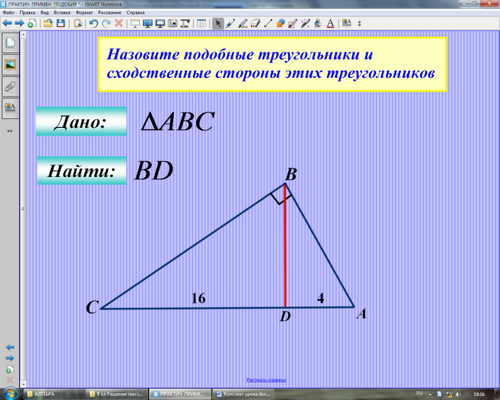
(Вторую задачу решают в тетрадях с комментариями.)

Учитель: Назовите подобные треугольники (признак), сходственные стороны этих треугольников, составьте пропорцию, выразите неизвестную величину и найдите ее.

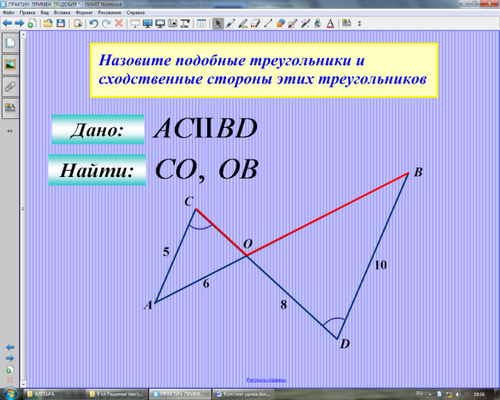
(Третью задачу решают фронтально, записи ведут и на доске, и в тетрадях.)

Учитель: Назовите подобные треугольники (признак), сходственные стороны этих треугольников, составьте пропорцию, выразите неизвестные величины и найдите их.

Учитель: Вернемся к вопросу об измерении высоты дерева.

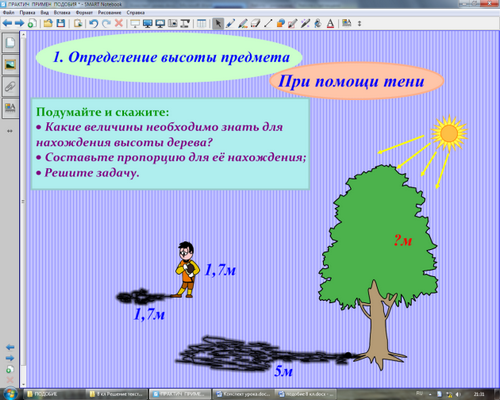
Подумайте и скажите:

- Можно ли с помощью тени измерить высоту дерева?

- На чем основан способ измерения высоты дерева?

- Назовите признак подобия треугольников.

- Какие величины для этого нужно знать?

- Составьте пропорцию.

- Решите задачу.

(учащиеся на доске маркером подписывают необходимые обозначения, составляют пропорцию, выражают высоту дерева через остальные компоненты)

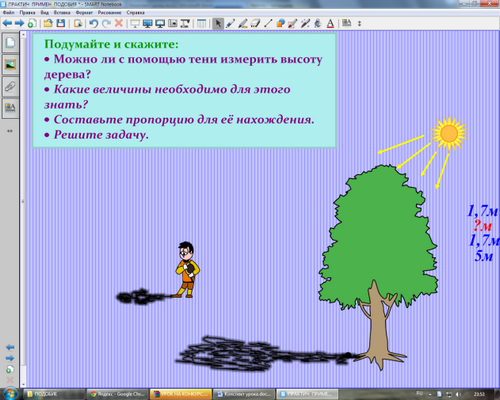
Устно. Определить высоту дерева с приведенными данными.

Учитель: С помощью тени еще в 6 веке до нашей эры смог определить высоту огромной пирамиды греческий ученый Фалес Милетский. Послушайте притчу.

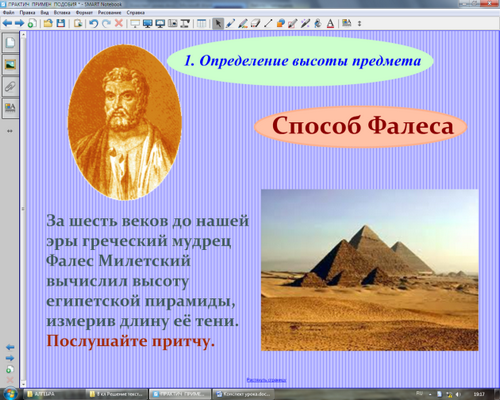
Притчу рассказывает ученик, подготовившийся заранее.

«Усталый чужеземец пришёл в страну Великого Хапи. Солнце уже садилось, когда он подошёл к великолепному дворцу фараона. Он что-то сказал слугам. По мановению руки распахнулись перед ним двери и провели его в приёмную залу. И вот он стоит в запылённом походном плаще, а перед ним на золоченом троне сидит фараон. Рядом стоят высокомерные жрецы, хранители великих тайн природы.

- Кто ты? - спросил верховный жрец.

- Зовут меня Фалес. Родом я из Милета.

Жрец надменно продолжал:

- Так это ты похвалялся, что сможешь измерить высоту пирамиды, не взбираясь на неё? - Жрецы согнулись от хохота.

- Будет хорошо, - насмешливо продолжал жрец, - если ты ошибёшься не более чем на 100 локтей.

- Я могу измерить высоту пирамиды и ошибусь не более чем на пол-локтя. Я сделаю это завтра.

Лица жрецов потемнели. Какая наглость! Этот чужеземец утверждает, что может вычислить то, чего не могут они - жрецы великого Египта.

- Хорошо, - сказал фараон. - Около дворца стоит пирамида, мы знаем её высоту. Завтра проверим твоё искусство».

На следующий день Фалес нашёл длинную палку, воткнул её в землю чуть поодаль пирамиды. Дождался определённого момента. Провёл некоторые измерения, сказал способ определения высоты пирамиды и назвал её высоту.

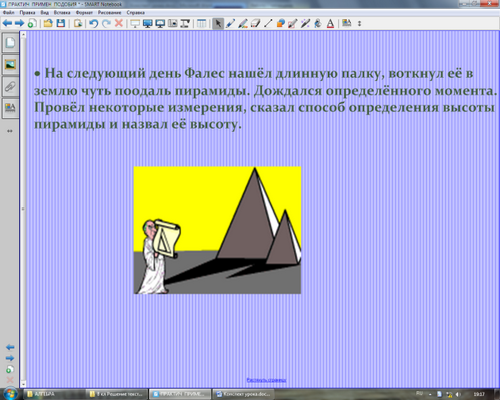
(Далее ученик рассказывает, как Фалес вычислил высоту пирамиды, используя подобные треугольники по представленному на экране рисунку.)

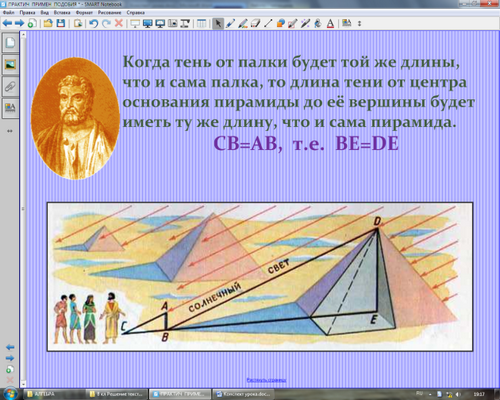
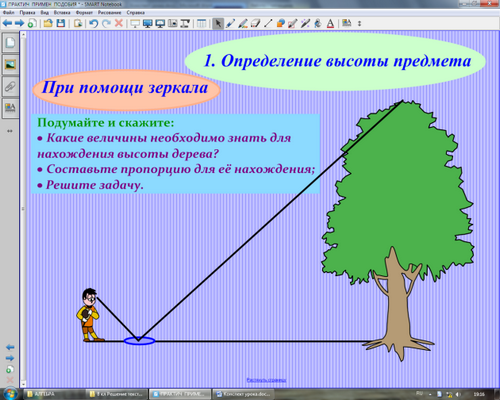
Учитель: оказывается, для определения высоты предмета существуют и другие способы. Например, можно воспользоваться зеркалом (лужей) так, как показано на рисунке.

Подумайте и скажите:

- на чем основан способ измерения высоты дерева?

- назвать признак подобия треугольников;

- какие величины надо знать для нахождения высоты дерева?

- составьте пропорцию для ее нахождения;

- выразите неизвестную величину.

(учащиеся на доске маркером подписывают необходимые обозначения, составляют пропорцию, выражают высоту дерева через остальные компоненты)

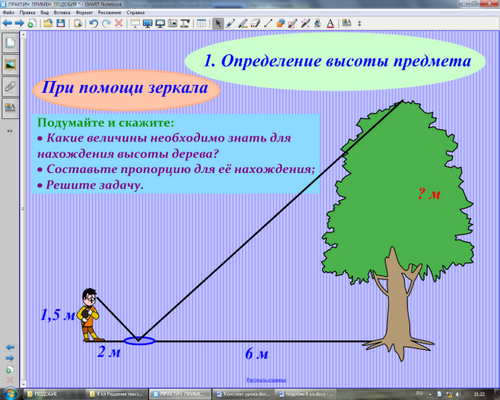
(Далее предлагается вычислить высоту дерева с приведенными данными.)

Учитель: интересный способ вычисления высоты скалы приводит французский писатель Жуль Верн в своей книге «Таинственный остров»

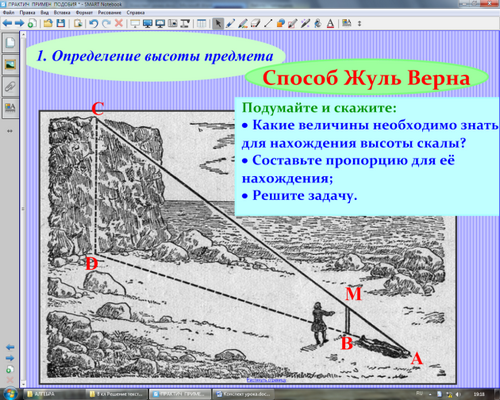
Посмотрите на рисунок и скажите, как люди, попавшие на необитаемый остров, измерили высоту скалы?

Подумайте и скажите:

- на чем основан способ измерения высоты скалы?

- назвать признак подобия треугольников;

- какие величины надо знать и легко измерить на практике для нахождения высоты скалы?

- составьте пропорцию для ее нахождения;

- выразите высоту скалы через остальные величины.

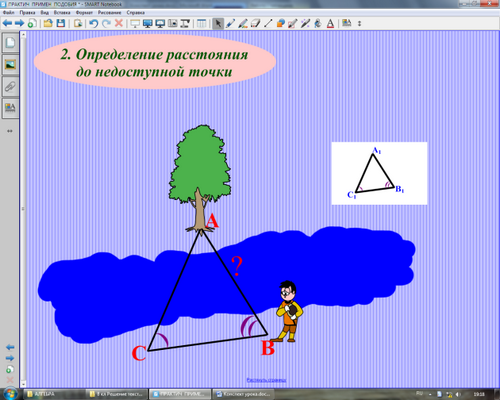
Учитель: С помощью подобных треугольников, можно измерить не только высоту предмета, но и расстояние до недоступной точки, как в случае, показанном на рисунке. Кто может объяснить способ нахождения расстояния от мальчика до дерева на противоположном берегу реки? (Выслушать ответы учащихся, помочь, если возникнут затруднения)

Учитель: А вот где еще смогло пригодиться знание подобных треугольников и о русской смекалке расскажет…

Рассказ ученика, заранее подготовившегося к уроку.

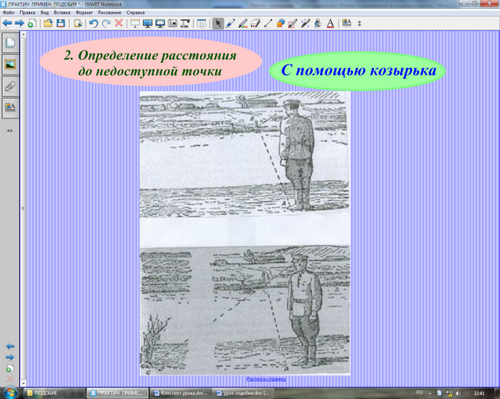
Вот как этот способ пригодился старшему сержанту Куприянову во фронтовой обстановке. Его отделению было приказано измерить ширину реки, через которую предстояло организовать переправу…

Подобравшись к кустарнику вблизи реки, отделение Куприянова залегло, а сам Куприянов вместе с солдатом Карповым выдвинулся ближе к реке, откуда был хорошо виден занятый фашистами берег. В таких условиях измерять ширину реки нужно было на глаз.

─ Ну-ка, Карпов, сколько? - спросил Куприянов.

─ По-моему, не больше 100 - 110 м, − ответил Карпов. Куприянов был согласен со своим разведчиком, но для контроля решил измерить ширину реки при помощи «козырька». Способ этот состоит в следующем. Надо стать лицом к реке и надвинуть фуражку на глаза так, чтобы нижний обрез козырька точно совпал с линией противоположного берега. Козырёк можно заменить ладонью руки или записной книжкой, плотно приложенной ребром ко лбу. Затем, не изменяя положения головы, надо повернуться направо или налево, или даже назад (в ту сторону, где поровней площадка, доступная для измерения расстояния) и заметить самую дальнюю точку, видимую из-под козырька (ладони, записной книжки).

Расстояние до этой точки и будет примерно равно ширине реки.

Этим способом и воспользовался Куприянов. Он быстро встал в кустах, приложил ко лбу записную книжку, также быстро повернулся и завизировал дальнюю точку. Затем вместе с Карповым он ползком добрался до этой точки, измеряя расстояние шнуром. Получилось 105 м.

Куприянов доложил командованию полученные им данные.

Учитель:

- на чем основан способ измерения?

- назвать признак подобия треугольников;

- какие величины надо для этого знать?

Подведем итог:

- Могут ли нам пригодиться знания подобных треугольников в жизни? (Да)

- Где можно применить эти знания? (для нахождения высоты предмета и определение расстояния до недоступной точки)

- Чему вы научились сегодня на уроке? (находить высоту предмета при помощи тени, при помощи зеркала, способом Ж.Верна, и определять расстояние до недоступной точки)

- Какие теоретические знания нам пригодились? (Признаки подобия треугольников)

Учитель: Многие разделы геометрии имеют практическое значение. Например, тема «Подобные треугольники». С помощью подобных треугольников можно вычислить высоту предмета или найти расстояние до недоступной точки. Эти знания могут пригодиться при строительстве различных дорог (железных, шоссейных и т.д.), плотин, гидроэлектростанций, мостов, сооружений линий электропередач, строительстве городов, сёл, и многое-многое другое требует проведение измерительных работ на местности.

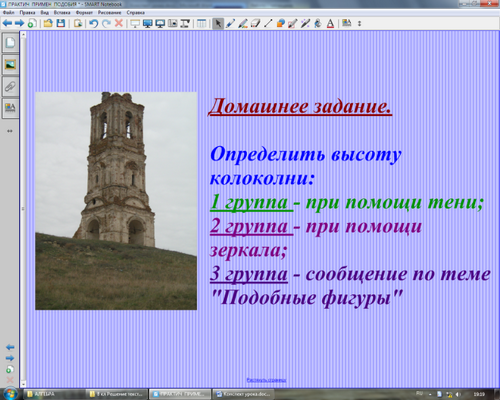
Домашнее задание.

Определить высоту колокольни (местной достопримечательности - середина 18 в)

1 группа - при помощи тени (сделать несколько замеров)

2 группа - при помощи зеркала (сделать несколько замеров)

3 группа - сообщение на тему «Подобные фигуры»

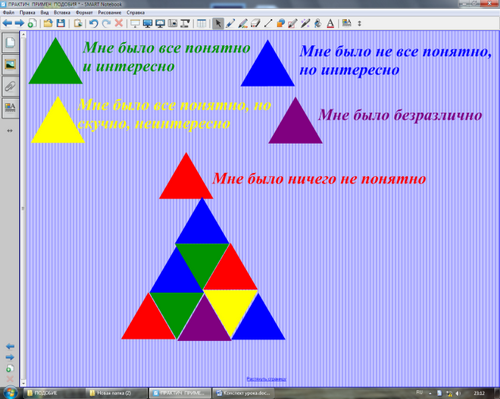
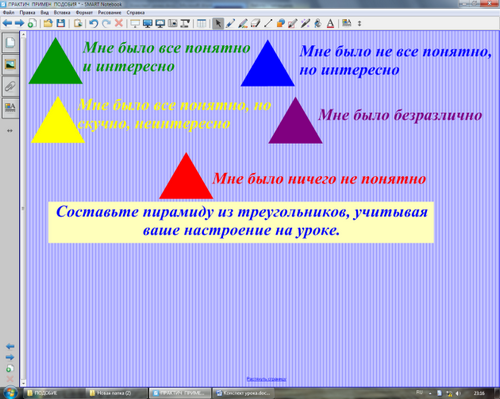
Рефлексия

Составить пирамиду, учитывая настроение на уроке:

Зеленый - мне было все понятно и интересно

Синий - мне было не все понятно, но интересно

Желтый - мне было все понятно, но не интересно

Фиолетовый - мне было безразлично

Красный - мне было ничего не понятно

Например, может получиться такая пирамида.