- Учителю
- Урок алгебры в 10 классе
Урок алгебры в 10 классе
Конспект - сценарий урока
Тема: Преобразование графиков тригонометрических функций
Цель: Развитие логического и алгоритмического мышления учащихся.
Учебные задачи, направленные на достижение личностных результатов обучения: Развивать представление о математике как форме описания и методе познания действительности, формировать коммуникативные компетентности.
Учебные задачи, направленные на достижение метапредметных результатов обучения: Формировать умение преобразовывать модели для решения задач, умение действовать по предложенному алгоритму, умение строить причинно-следственные связи, умение применять ИКТ-технологии; формировать умение ставить цель, умение осуществлять контроль по результату и способу действия, проводить самооценку уровня понимания, оценивать собственные возможности решения задачи; формировать умение устраивать эффективные групповые обсуждения для принятия совместных решений, умение формулировать и аргументировать.
Учебные задачи, направленные на достижение предметных результатов обучения: Осуществить коррекцию и обобщение знаний о видах преобразований графиков на примере тригонометрических функций.
Оборудование урока: компьютер, мультимедийный проектор, интерактивная доска, презентация к уроку, видеоролик, раздаточный материал (алгоритмы).
Технологическая карта урока
№ п/п
Этапы урока
Деятельность учителя
Деятельность ученика
Формируемые УУД
I.Мотивационно-ориентировочный блок
1.
Этап актуализации
-А Вы когда-нибудь задумывались над тем, что большинство Ваших действий повторяется изо дня в день? Для того чтобы прийти к определенному результату, нужно выполнить определенную последовательность действий. Вся наша жизнь состоит из последовательности действий, нарушение которой может привести к разным последствиям, как к хорошим, так и к плохим. Помните сказку «Репка»? По-моему, яркий пример действий, который привел к положительному результату.
Конечная последовательность строго определенных действий, приводящих к однозначному решению поставленной задачи…Что это?
Приведите пожалуйста примеры алгоритмов из жизни или с Ваших уроков. , слайды 1-2
- Предлагаю Вам выполнить действия по следующему алгоритму.
Организует работу по повторению преобразований графиков в форме «Математического диктанта», графики функций изображены на экране. , слайды 3-6. №1-№3. По графику запишите формулу. №4. Восстановите коэффициенты в формуле
y=A sin( x+
x+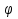 ), для этого:
), для этого: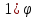 возьмите из третьей формулы в №1, увеличив это число в 3 раза; 2) А возьмите из первой формулы в №2, умножив это число на 4; 3)
возьмите из третьей формулы в №1, увеличив это число в 3 раза; 2) А возьмите из первой формулы в №2, умножив это число на 4; 3)  возьмите из второй формулы в №3, увеличив это число в 6 раз.
возьмите из второй формулы в №3, увеличив это число в 6 раз.
Ответы (на закрытой доске):
№1. 1) y=sinx, 2) y=sin(x+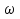 ),3) y=sin(x-
),3) y=sin(x- 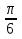 ), 4)y=sinx+1, 5)y=sinx-1,5;
), 4)y=sinx+1, 5)y=sinx-1,5;
№2.1)y=0,5sinx, 2)y=2,5cosx;
№3.1) y=sin2x, 2) y=cos0,5x; №4. 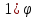 =-
=-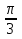 , 2)А=2, 3)
, 2)А=2, 3)  =3.
=3.
При необходимости организует коррекцию и обсуждение.
- Алгоритм.
- Рецепты блюд, режим дня, алгоритмы в информатике, разбор слова по составу в русском языке, выполнение лабораторной работы на уроках физики или химии, надевание противогаза на ОБЖ, решение неравенств методом интервалов на алгебре…
Индивидуально выполняют шаги предложенного алгоритма. Записывают ответы в тетрадях.
Ученик, быстрее всех справившийся с заданием, записывает формулу на доске:
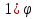 y=2sin(
y=2sin(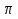 x -
x - 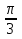 ).
).
Сравнивают свои ответы с ответами на доске, исправляют ошибки, отвечают на вопросы.
Умение преобразовывать модели для решения задач.
Умение действовать по предложенному алгоритму.
Умение осуществлять контроль и проводить самооценку уровня понимания.
Умение формулировать и аргументировать.
2.
Этап проблематизации
Включает видеоролик.
Задает вопросы:
- Как связано видео и полученная формула?
- Запишите формулы гармонических колебаний (1 ученик на доске).
- Давайте вспомним из физики, как называются коэффициенты в формулах гармонических колебаний
y=A sin( x+
x+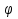 ) и y=A cos(
) и y=A cos( x+
x+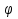 ).
).
, слайд 7
- Сможете ли Вы без осциллографа создать картинку данного гармонического колебания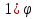
y=2sin(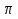 x -
x - 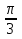 )?
)?
- Какие затруднения могут у Вас возникнуть?
Возможные ответы:
- Мы видим осциллограф, на экране которого - синусоида. Эта картинка дает нам представление о переменном токе. А формула описывает этот процесс. Процесс называется гармонические колебания.
Записывают в тетрадь формулы гармонических колебаний.
- A - амплитуда колебания,  - частота колебания,
- частота колебания, 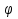 - начальная фаза колебания.
- начальная фаза колебания.
- Задачи на построение графика, где присутствуют одновременно все коэффициенты не встречались.
Умение строить причинно-следственные связи, строить логическое рассуждение.
Умение формулировать и аргументировать.
Умение оценивать собственные возможности решения задачи.
3.
Этап целеполагания
Подводит учащихся к формулированию цели урока:
- Какую цель можно поставить на этот урок? , слайд 8
Принимают учебные задачи, формулируют цель предстоящей деятельности:
- Построить график гармонического колебания y=2sin(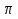 x -
x - 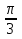 ).
).
Умение ставить цель учебной деятельности.
II.Организационно-деятельностный блок
1.
Этап моделирования
Проводит актуализацию опорных знаний и способов действий.
- Какие знания Вам необходимы для построения графика гармонического колебания?
- За какое преобразование графика отвечает каждый коэффициент?
- Каков период данной функции?
Ученики отвечают, что умеют строить график функции y=sinx, знают ее свойства, умеют выполнять преобразования графиков (сдвиги и отдельно сжатия - растяжения), умеют вычислять период.
Умение формулировать и аргументировать.
Умение оценивать собственные возможности решения задачи.
2.
Этап конструирования
- Предлагаю Вам в качестве помощи в решении поставленной задачи готовые алгоритмы построения графиков гармонических колебаний.
Организует работу в группах по построению графика гармонического колебания y=2sin(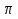 x -
x - 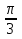 ) по трем разным алгоритмам (по две группы на один алгоритм). , слайды 9-11. , раздаточный материал. Алгоритм 1
) по трем разным алгоритмам (по две группы на один алгоритм). , слайды 9-11. , раздаточный материал. Алгоритм 1
Построим график функции y=Asin( x+
x+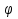 ) , y=Acos(
) , y=Acos( x+
x+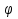 ).
).
1.Строим график основной функции y=sin x, y=cos x.
2.Сдвигаем этот график на 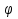 единиц по оси х.
единиц по оси х.
3. Сжимаем предыдущий график в  раз к оси у или растягиваем его в 1/
раз к оси у или растягиваем его в 1/ раз от оси у.
раз от оси у.
4. Растягиваем последний график в А раз от оси х или сжимаем в 1/А раз к оси х.
Совет: Все преобразования можно производить с полуволной, а затем построить весь график.
Алгоритм 2
Построим график функции y=Asin( x+
x+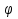 ) , y=Acos(
) , y=Acos( x+
x+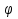 ).
).
1. Преобразуем формулу y=Asin( x+
x+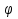 ) к виду y=Asin
) к виду y=Asin (x+
(x+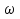 ), формулу y=Acos(
), формулу y=Acos( x+
x+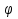 ) к виду y=Acos
) к виду y=Acos (x+
(x+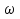 ).
).
2. Построим график основной функции y=sin x, y=cos x.
3. Сжимаем этот график в  раз к оси у или растягиваем в 1/
раз к оси у или растягиваем в 1/ раз от оси у.
раз от оси у.
4. Растягиваем последний график в А раз от оси х или сжимаем в 1/А раз к оси х.
5. Сдвигаем предыдущий график на 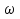 единиц по оси х.
единиц по оси х.
Совет: Все преобразования можно производить с полуволной, а затем построить весь график.
Алгоритм 3
Построим график функции y=Asin( x+
x+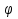 ) , y=Acos(
) , y=Acos( x+
x+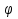 ).
).
1. Найдем точки пересечения графика с осью х, для чего составим уравнение Asin( x+
x+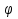 )=0 ( Acos(
)=0 ( Acos( x+
x+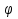 )=0)
)=0)
2. Решим уравнение:  x+
x+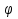 =
= (
(  x+
x+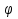 =
=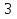 )
)
x=-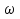 +
+ /
/ ( x=
( x=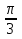 /
/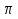 -
- 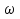 +
+ /
/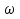
3. Дадим параметру k два соседних значения (например, 0 и 1) и вычислим соответствующие значения х1 и х2.
4. Точки А(х1; 0) и В(х2; 0) являются концами одной полуволны.
5. Вычислим координату середины отрезка АВ: х3=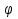 .
.
6. Вычислим f(х3). Точка С(х3; f(х3)) является верхней или нижней точкой искомой полуволны.
7. По трем точкам А, В, С строим полуволну, а затем строим весь график.
Изменяет состав групп, объединяя группы с одинаковыми алгоритмами с целью принятия общего решения по построению графика. Дает задание: записать этапы построения графика в соответствии с алгоритмом и выбрать 2-х учеников для презентации.
Возвращает учащихся на места.
Работают в группах. Изучают предложенный алгоритм и строят графики в тетрадях.
Собираются по две группы. Обсуждают построение, исправляют ошибки, записывают этапы построения и выбирают 2-х учеников для презентации.
Рассаживаются по местам.
Умение преобразовывать модели для решения задач,
умение действовать по предложенному алгоритму.
Умение осуществлять контроль по результату и способу действия.
Умение устраивать эффективные групповые обсуждения для принятия совместных решений.
3.
Этап презентации
Вызывает по 2 ученика для объяснения построения по каждому из трех алгоритмов.
При необходимости организует коррекцию и обсуждение.
Сохраняет все построенные графики на интерактивной доске.
Обращает внимание, что применение любого из алгоритмов привело к одинаковому решению.
- Какие свойства алгоритмов Вам известны?
- Обладают ли предложенные алгоритмы этими свойствами? , слайд 12
Один ученик записывает этапы построения на доске и комментирует записи. Второй ученик одновременно строит график на интерактивной доске.
Алгоритм 1. 1) y=sinx;
2) y=sin(x-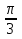 ); 3) y=sin(3x-
); 3) y=sin(3x-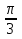 );
);
4) y=2sin(3x-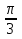 ).
).
Алгоритм 2. 1)2sin(3x-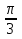 )=2sin3(x-
)=2sin3(x- 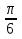 ); 2) y=sinx;
); 2) y=sinx;
3) y=sin3x; 4) y=2sin3x;
5) y=2sin3(x- 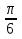 ).
).
Алгоритм 3.1) 2sin(3x-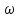 =0;
=0;
2) 3x-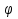 x=
x= 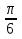 +
+  ;
;
3) k=-1, x1=0; k=0, x2=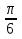 ; 4)
; 4)
А (0; 0), В(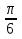 ; 0); 5) x3=
; 0); 5) x3=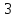 ;
;
6) f(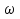 )=-2; С(
)=-2; С(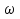 ; -2).
; -2).
Остальным ученикам предлагается записать этапы построения по «чужим» алгоритмам в тетрадь.
Задают вопросы, корректируют ответы.
- Дискретность, результативность, массовость,
детерминированность, понятность.
Умение формулировать и аргументировать.
Умение применять ИКТ-технологии.
Умение осуществлять контроль и проводить самооценку уровня понимания.
Умение строить причинно-следственные связи, строить логическое рассуждение.
III.Рефлексивно-оценочный блок
Выставляет оценки отвечавшим ученикам.
Предлагает задание, контролирующее уровень понимания (фронтально): По построенному графику определить способ построения и записать формулу: ,слайды 13-15
1.
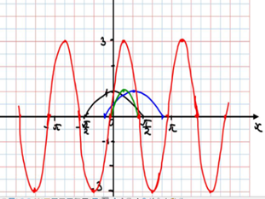
2.
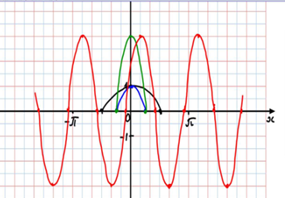
3.
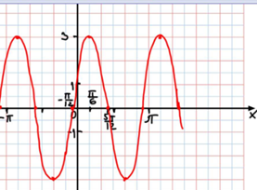
Домашнее задание: Придумать формулу гармонического колебания и построить его график по трем алгоритмам.
Предлагает высказаться о достижении поставленной цели, о необходимости алгоритмов в нашей жизни и заполнить «Лист самооценки».
Лист самооценки
(оценить по 3-бальной шкале: 3 - умею хорошо, 2 - умею, но есть чему поучиться; 1 - не умею)
задание
критерии
1.«Математический диктант»
2.Построение графика
y=2sin(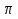 x -
x - 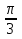 )
)
1.Умею действовать по предложенному алгоритму
2.Умею преобразовывать модели:
а) по графику записывать формулу (для 1);
б) по формуле строить график (для 2).
3.Умею осуществлять контроль и коррекцию результата (находить и исправлять ошибки)
4.Умею применять различные виды преобразования графиков.
5.Умею работать в группе (для 2):
а) степень активности;
б) умение прислушиваться к мнению других.
-Ну, вот и время пролетело,
Подходит наш урок к концу.
Работали вы все умело
По алгоритму моему.
Была поставлена задача
С которой справились вы все.
Пусть вам сопутствует и дальше
Удача и в учебе, и в труде!
, слайд16
Высказывают свое мнение.
Выполняют задание устно, обсуждают данные ответы.
Записывают в тетрадь.
Отвечают на вопросы и заполняют «Лист самооценки».
Умение формулировать и аргументировать.
Умение преобразовывать модели для решения задач.
Умение строить причинно-следственные связи, строить логическое рассуждение.
Умение осуществлять контроль по результату и способу действия.
Умение проводить самооценку.