Опорные задачи по теме Перпендикулярность прямой и плоскости (10 класс)

Опорные задачи

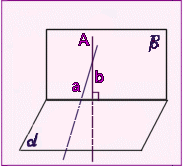
Тема «Перпендикулярность прямой и плоскости»Докажите, что через любую точку прямой в пространстве можно провести перпендикулярную ей прямую.

Решение: пусть а - прямая и А - точка на ней. Возьмем любую точку Х вне прямой а и проведем через эту точку и прямую а плоскость . В плоскости через точку А можно провести прямую b, перпендикулярную а.

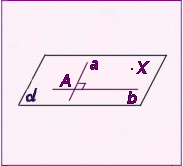
Докажите, что через любую точку А можно прoвести прямую, перпендикулярную данной плоскости .

Решение: Проведем в плоскости две пересекающиеся прямые с и b. Через точку их пересечения проведем плоскости и перпендикулярные прямым b и с соответственно. Они пересекаются по некоторой прямой а. Прямая а перпендикулярна прямым b и с, значит и плоскости . Проведем теперь через точку А прямую d, параллельную а. По теореме (Если плоскость перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой) она перпендикулярна плоскости .

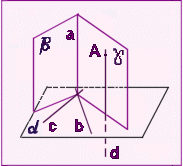
Докажите, что если прямая параллельна плоскости, то все ее точки находятся на одинаковом расстоянии от плоскости.

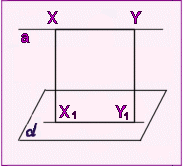
Решение: Пусть а - данная прямая и - данная плоскость. Возьмем на прямой а две произвольные точки Х и Y. Их расстояния до плоскости - это длины перпендикуляров ХХ₁ и YY₁, опущенных на эту плоскость. По теореме (Две прямые, перпендикулярные одной и той же плоскости, параллельны) прямые ХХ₁ и YY₁ параллельны, следовательно, лежат в одной плоскости. Эта плоскость пересекает плоскость по прямой Х₁Y₁.Прямая а параллельна прямой Х₁Y₁, так как не пересекает содержащую её плоскость . Итак у четырехугольника ХХ₁YY₁ противолежащие стороны параллельны. Следовательно, он параллелограмм, а значит ХХ₁=YY₁.

Через центр вписанной в треугольник окружности проведена прямая, перпендикулярная плоскости треугольника. Докажите, что каждая точка этой прямой равноудалена от сторон треугольника.

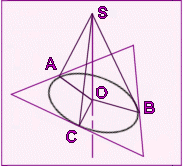
Решение: Пусть А, В, С - точки касания сторон треугольника с окружностью, О - центр окружности и S - точка на перпендикуляре. Так как радиус ОА перпендикулярен стороне треугольника, то по теореме о ТРЕХ ПЕРПЕНДИКУЛЯРАХ Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна ее проекции, то она перпендикулярна наклонной.

И обратно: Если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна и проекции наклонной) отрезок SА есть перпендикуляр к этой стороне, а его длина - расстояние от точки S до стороны треугольника. по теореме Пифагора SА²=OА²+SO²=r²+SO², где r - радиус вписанной окружности. Аналогично получаем SВ²=r²+SO² и SС²=r²+SO², т.е. все расстояния от точки S до сторон треугольника равны.

Даны прямая а и плоскость . Проведите через прямую а плоскость, перпендикулярную плоскости .

Решение: Через произвольную точку прямой а проводим прямую b, перпендикулярную плоскости . Через прямые а и b проводим плоскость . Плоскость перпендикулярна плоскости по теореме (Если плоскость проходит через прямую перпендикулярную другой плоскости</<font face="Times New Roman, serif">, то эти плоскости перпендикулярны).