- Учителю
- Рабочая программ по алгебре 7 класс
Рабочая программ по алгебре 7 класс
Пояснительная записка
Рабочая программа по алгебре для 7 класса, разработана в соответствии с основными положениями Федерального государственного образовательного стандарта начального общего образования, требованиями Примерной основной образовательной программы общего образования, Основной образовательной программы начального общего образования школы, на основе авторской программы Алимова Ш.А., приказ Министерства образования и науки Российской Федерации от 31.03.2014 № 253 «Об утверждении федеральных перечней учебников, рекомендованных к использованию в образовательном процессе в образовательных учреждений, реализующих образовательные программы общего образования и имеющих государственную аккредитацию на 2009/2010 учебный год»;
Целью изучения курса алгебры 7 класса является развитие вычислительных и формально-оперативных алгебраических умений до уровня, позволяющего уверенно использовать их при решении задач математики и смежных предметов, усвоение аппарата уравнений и неравенств как основного средства математического моделирования прикладных задач, осуществление функциональной подготовки школьников.
Курс характеризуется повышением теоретического уровня обучения, постепенным усилением роли теории обобщений и дедуктивных заключений.
Изучение математики на ступени основного общего образования направлено на достижение следующих целей:
-
Овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
-
Интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясность и точность мысли, критичность мышления, интуиция, логическое мышление, элементы алгоритмической культуры, пространственных представлений, способность к преодолению трудностей;
-
Формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
-
Воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса.
Цели обучения математики в общеобразовательной школе определяются ее ролью в развитии общества в целом и формировании личности каждого отдельного человека
Математика играет важную роль в общей системе образования. Но математика в школе не наука и даже не основа науки, а учебный предмет. Математика в школе - предмет не естественно научный, а гуманитарный.
В учебном предмете, в отличие от науки, мы не обязаны все доказывать. Более того, в ряде случаев правдоподобные рассуждения или толкования, опирающиеся на графические модели, на интуицию, имеют для школьников более весомую общекультурную ценность, чем формальные доказательства.
Сложные математические понятия вводятся:
- когда у учащихся накоплен достаточный опыт для адекватного восприятия вводимого понятия опыт, содействующий пониманию всех слов, содержащихся в определении (вербальный опыт), и опыт использования понятия на наглядно-интуитивном и рабочем уровнях (генетический опыт);
- когда у учащихся появилась потребность в формальном определении понятия.
Гуманитарный потенциал школьного курса алгебры состоит в том, что владение математическим языком и математическим моделированием позволяет ученику лучше ориентироваться в природе и обществе, способствует развитию речи не в меньшей степени, чем уроки русского языка и литературы. Математика гуманитарный предмет, который позволяет ученику правильно ориентироваться в окружающей действительности и ум в порядок приводит.
Изучение математики способствует эстетическому воспитанию человека, пониманию красоты и изящества математических рассуждений, восприятию геометрических форм, развивает воображение, пространственные представления. История развития математического знания дает возможность пополнить запас историко-научных знаний учащихся, сформировать у них представления о математике как части общечеловеческой культуры. Знакомство с основными историческими вехами возникновения и развития математической науки, судьбами великих открытий, именами людей, творивших науку, должно войти в интеллектуальный багаж каждого культурного человека.
Алгебра нацелена на формирование математического аппарата для решения задач из математики, смежных предметов, окружающей реальности. Язык алгебры подчеркивает значение математики как языка для построения математических моделей, процессов и явлений реального мира.
Одной из основных задач изучения алгебры является развитие алгоритмического мышления, необходимого, в частности, для освоения курса информатики; овладения навыками дедуктивных рассуждений. Преобразование символических форм вносит свой специфический вклад в развитие воображения, способностей к математическому творчеству.
Другой важной задачей изучения алгебры является получение школьниками конкретных знаний о функциях как важнейшей математической модели для описания и исследования разнообразных процессов (равномерных, равноускоренных, периодических и др.) для формирования у школьников представления о роли математики в развитии цивилизации и культуры.
Элементы логики, комбинаторики, статистики и теории вероятностей становятся обязательным компонентом школьного образования, усиливающим его прикладное и практическое значение.
При изучении этого компонента обогащаются представления о современной картине мира и методов его исследования, развиваются представления о числе и роли вычислений в человеческой практике, используются функционально-графические представления для описания и анализа реальных зависимостей.
Важной задачей этого компонента является формирование функциональной грамотности умений воспринимать и анализировать информацию, представленную в различных формах, понимать вероятностный характер многих реальных зависимостей, производить простейшие вероятностные расчеты.
Образовательные и воспитательные задачи обучения алгебре должны решаться комплексно с учетом возрастных особенностей обучающихся, специфики алгебры как учебного предмета, определяющего её роль и место в общей системе школьного обучения и воспитания. Учителю предоставляется право самостоятельного выбора методических путей и приемов решения этих задач. В организации учебно-воспитательного процесса важную роль играют задачи. Они являются и целью, и средством обучения и математического развития учащихся. При планировании уроков следует иметь в виду, что теоретический материал осознается и усваивается преимущественно в процессе решения задач. Организуя решение задач, целесообразно шире использовать дифференцированный подход к учащимся. Дифференциация требований к учащимся на основе достижения всеми обязательного уровня подготовки способствует разгрузке школьников, обеспечивает их посильной работой и формирует у них положительное отношение к учебе. Важным условием правильной организации учебно-воспитательного процесса является выбор учителем рациональной системы методов и приемов обучения, сбалансированное сочетание традиционных и новых методов обучения, оптимизированное применение объяснительно-иллюстрированных и эвристических методов, использование технических средств. Учебный процесс необходимо ориентировать на рациональное сочетание устных и письменных видов работы, как при изучении теории, так и при решении задач. Внимание учителя должно быть направлено на развитие речи учащихся, формирование у них навыков умственного труда планирование своей работы, поиск рациональных путей её выполнения, критическую оценку результатов.
Требования к уровню подготовки ученика 7 класса
В результате изучения алгебры ученик должен
знать/понимать
-
существо понятия математического доказательства; приводить примеры доказательств;
-
существо понятия алгоритма; приводить примеры алгоритмов;
-
как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;
-
как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;
-
как потребности практики привели математическую науку к необходимости расширения понятия числа;
-
вероятностный характер многих закономерностей окружающего мира; примеры статистических закономерностей и выводов.
Арифметика
уметь
-
выполнять устно арифметические действия: сложение и вычитание двузначных чисел и десятичных дробей с двумя знаками, умножение однозначных чисел, арифметические операции с обыкновенными дробями с однозначным знаменателем и числителем;
-
записывать большие и малые числа с использованием целых степеней десятки;
-
выполнять арифметические действия с рациональными числами, сравнивать рациональные и действительные числа; находить в несложных случаях значения степеней с натуральными показателями; находить значения числовых выражений;
использовать приобретенные знания и умения в практической деятельности и повседневной жизнидля:
-
решения несложных практических расчетных задач, в том числе c использованием при необходимости справочных материалов, калькулятора, компьютера;
-
устной прикидки и оценки результата вычислений; проверки результата вычисления, с использованием различных приемов;
-
интерпретации результатов решения задач с учетом ограничений, связанных с реальными свойствами рассматриваемых процессов и явлений.
Алгебра
уметь
-
составлять буквенные выражения и формулы по условиям задач; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, осуществлять подстановку одного выражения в другое; выражать из формул одну переменную через остальные;
-
выполнять основные действия со степенями с натуральными показателями, с многочленами; выполнять разложение многочленов на множители; выполнять тождественные преобразования рациональных выражений;
-
решать линейные уравнения и системы двух линейных уравнений;
-
решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи;
-
определять координаты точки плоскости, строить точки с заданными координатами;
-
находить значения функции, заданной формулой, таблицей, графиком по ее аргументу; находить значение аргумента по значению функции, заданной графиком или таблицей;
-
определять свойства функции по ее графику; применять графические представления при решении уравнений, систем;
-
описывать свойства изученных функций, строить их графики;
использовать приобретенные знания и умения в практической деятельности и повседневной жизнидля:
-
выполнения расчетов по формулам, для составления формул, выражающих зависимости между реальными величинами; для нахождения нужной формулы в справочных материалах;
-
моделирования практических ситуаций и исследования построенных моделей с использованием аппарата алгебры;
-
описания зависимостей между физическими величинами соответствующими формулами, при исследовании несложных практических ситуаций;
-
интерпретации графиков реальных зависимостей между величинами.
Элементы логики, комбинаторики, статистики и теории вероятностей
уметь
-
извлекать информацию, представленную в таблицах, на диаграммах, графиках; составлять таблицы, строить диаграммы и графики;
-
вычислять средние значения результатов измерений;
-
находить частоту события, используя собственные наблюдения и готовые статистические данные;
-
решать комбинаторные задачи путем систематического перебора возможных вариантов и с использованием правила умножения;
использовать приобретенные знания и умения в практической деятельности и повседневной жизнидля:
-
выстраивания аргументации при доказательстве и в диалоге;
-
распознавания логически некорректных рассуждений;
-
записи математических утверждений, доказательств;
-
анализа реальных числовых данных, представленных в виде диаграмм, графиков, таблиц;
-
решения практических задач в повседневной и профессиональной деятельности с использованием действий с числами, процентов, длин, площадей, объемов, времени, скорости;
-
понимания статистических утверждений.
II. Содержание учебного предмета.
1. Повторение материала 6 класса
Цель - повторение пройденного материала, обобщение и систематизация.
2. Алгебраические выражения
Числовые и алгебраические выражения.Формулы. Свойства арифметических действий. Правила раскрытия скобок.
Цель - систематизировать и обобщить сведения о преобразовании выражений, полученные учащимися в курсе математики 5,6 классов.
Знать какие числа являются целыми, дробными, рациональными, положительными, отрицательными и др.; свойства действий над числами; знать и понимать термины: числовое выражение, выражение с переменными, значение выражения, среднее арифметическое, размах, мода и медиана ряда данных.
Уметь осуществлять в буквенных выражениях числовые подстановки и выполнять соответствующие вычисления; сравнивать значения буквенных выражений при заданных значениях входящих в них переменных; применять свойства действий над числами при нахождении значений числовых выражений.
3. Уравнения с одним неизвестным
Уравнение и его корни. Уравнения, сводящиеся к линейным. Решение задач с помощью уравнений.
Цель -совершенствовать умения решения линейных уравнений и текстовых задач, решаемых с помощью уравнений.
Знатьопределение линейного уравнения, корня уравнения, области определения уравнения.
Уметь решать линейные уравнения и уравнения, сводящиеся к ним; составлять уравнение по тексту задачи.
4. Одночлены и многочлены
Степень с натуральным показателем. Свойства степени. Одночлен. Стандартный вид одночлена. Многочлены. Сложение, вычитание и умножение многочленов.
Цель - выработать умение выполнять сложение, вычитание, умножение одночленов и многочленов.
Знать определение одночлена и многочлена, понимать формулировку заданий: «упростить выражение».
Уметь приводить многочлен к стандартному виду, выполнять действия с многочленами.
5. Разложение многочленов на множители
Вынесение общего множителя за скобки. Способ группировки. Формулы 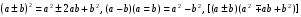 , куб суммы и куб разности, формула суммы кубов и разности кубов. Применение формул сокращённого умножения к разложению на множители.
, куб суммы и куб разности, формула суммы кубов и разности кубов. Применение формул сокращённого умножения к разложению на множители.
Цель - выработать умение выполнять разложение многочлена на множители, применять полученные навыки при решении уравнений, доказательстве тождеств.Знать способы разложения многочлена на множители, формулы сокращенного умножения. Уметьразложить многочлен на множители.
6. Алгебраические дроби
Цель - выработать умение применять в несложных случаях формулы сокращённого умножения для преобразования алгебраических дробей.
Знатьправила сокращения дроби, приведение дробей к общему знаменателю, арифметических действий над алгебраическими дробями.
Уметьпреобразовать алгебраическую дробь.
7. Функции
Функция, область определения функции, способы задания функции. График функции. Функция y=kx и её график. Линейная функция и ее график.
Цель - познакомить учащихся с основными функциональными понятиями и с графиками функций y=kx+b, y=kx.
Знатьопределения функции, области определения функции, области значений, что такое аргумент, какая переменная называется зависимой, какая независимой; понимать, что такое функция.
Уметьправильно употреблять функциональную терминологию (значение функции, аргумент, график функции, область определения, область значений); находить значения функций, заданных формулой, таблицей, графиком; решать обратную задачу; строить графики линейной функции, прямой и обратной пропорциональности; интерпретировать в несложных случаях графики реальных зависимостей между величинами, отвечая на поставленные вопросы.
8. Системы двух уравнений с двумя неизвестными
Системы уравнений с двумя переменными. Решение систем двух линейных уравнений с двумя переменными, графический способ. Решение задач методом составления систем уравнений.
Цель - познакомить учащихся со способами решения систем линейных уравнений с двумя переменными, выработать умение решать системы уравнений и применять их при решении текстовых задач.
Знать, что такое линейное уравнение с двумя переменными, система уравнений, знать различные способы решения систем уравнений с двумя переменными: способ подстановки, способ сложения; понимать, что уравнение - это математический аппарат решения разнообразных задач из математики, смежных областей знаний, практики.
Уметьправильно употреблять термины: «уравнение с двумя переменными», «система»; понимать их в тексте, в речи учителя, понимать формулировку задачи «решить систему уравнений с двумя переменными»; строить некоторые графики уравнения с двумя переменными; решать системы уравнений с двумя переменными различными способами.
9. Ведение в комбинаторику
Различные комбинации из трех элементов. Правило произведения. Подсчет вариантов.
10. Итоговое повторение
Закрепление знаний, умений и навыков, полученных на уроках по данным темам (курс алгебры 7 класса).
Шкала оценивания:
Критерии оценивания знаний, умений и навыковобучающихся по математике.
(Согласно Методическому письму «Направления работы учителей математики по исполнению единых требований преподавания предмета на современном этапе развития школы»)
Для оценки достижений учащихся применяется пятибалльная система оценивания. Нормы оценки:
1. Оценка письменных контрольных работ обучающихся по математике.
Ответ оценивается отметкой «5», если:
1) работа выполнена полностью;
2) в логических рассуждениях и обосновании решения нет пробелов и ошибок;
3) в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).
Отметка «4» ставится, если:
1) работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);
2)допущены одна ошибка или есть два - три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).
Отметка «3» ставится, если:
1) допущено более одной ошибки или более двух - трех недочетов в выкладках, чертежах или графиках, но обучающийся обладает обязательными умениями по проверяемой теме.
Отметка «2» ставится, если:
1) допущены существенные ошибки, показавшие, что обучающийся не обладает обязательными умениями по данной теме в полной мере.
Отметка «1» ставится, если:
1)работа показала полное отсутствие у обучающегося обязательных знаний и умений по проверяемой теме или значительная часть работы выполнена не самостоятельно.
Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии обучающегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные обучающемуся дополнительно после выполнения им каких-либо других заданий.
2.Оценка устных ответов обучающихся по математике
Ответ оценивается отметкой «5», если ученик:
-
полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;
-
изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;
-
правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;
-
показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;
-
продемонстрировал знание теории ранее изученных сопутствующих тем, сформированность и устойчивость используемых при ответе умений и навыков;
-
отвечал самостоятельно, без наводящих вопросов учителя;
-
возможны одна - две неточности при освещение второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя.
Ответ оценивается отметкой «4», если удовлетворяет в основном требованиям на оценку «5»,
но при этом имеет один из недостатков:
-
в изложении допущены небольшие пробелы, не исказившее математическое содержание ответа;
-
допущены один - два недочета при освещении основного содержания ответа, исправленные после замечания учителя;
-
допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.
Отметка «3» ставится в следующих случаях:
-
неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для усвоения программного материала (определены «Требованиями к математической подготовке учащихся» в настоящей программе по математике);
-
имелись затруднения или допущены ошибки в определении математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;
-
ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;
-
при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.
Отметка «2» ставится в следующих случаях:
-
не раскрыто основное содержание учебного материала;
-
обнаружено незнание учеником большей или наиболее важной части учебного материала;
-
допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.
Отметка «1» ставится, если:
-
ученик обнаружил полное незнание и непонимание изучаемого учебного материала или не смог ответить ни на один из поставленных вопросов по изученному материалу.
Итоговая оценка знаний, умений и навыков
1. За учебную четверть и за год знания, умения и навыки учащихся по математике оцениваются одним баллом.
2. Основанием для выставления итоговой оценки знаний служат результаты наблюдений учителя за повседневной работой учеников, устного опроса, текущих и итоговых контрольных работ. Однако последним придается наибольшее значение.
3. При выставлении итоговой оценки учитывается как уровень теоретических знаний ученика, так и овладение им практическими умениями и навыками. Однако ученику не может быть выставлена положительная итоговая оценка по математике, если все или большинство его текущих обучающих и контрольных работ, а также итоговая контрольная работа оценены как неудовлетворительные, хотя его устные ответы оценивались положительно.
№ урока
Учебно-тематическое планирование
Сроки
Требования федерального стандарта
НРК Государственного стандарта
Педагогические условия и условия их реализации (методы, формы)
Программное и учебное методическое обеспечение
Контрольный материал
Составляющие образованности
Предметно-информационная
Деятельностно-коммуникативная
Ценностно-ориентированная
-
Повторение 6 часов
-
Алгебраические выражения.
Понятие выражения, числового выражения, алгебраического выражения, значение выражения числовое равенство.
Знать какие равенства называются верные, порядок действий в числовом и алгебраическом выражении.
Понятие формула, четное, нечётное число, алгебраическая сумма.
Знать законы сложения и умножения.
Знать правила раскрытия скобок.
Уметь находить рациональное решение.
Уметь составить несложное буквенное выражение и формулы, осуществлять в выражении и формулах числовые подстановки, выражать в формулах одни переменные через другие.
Уметь решать текстовые задачи с использованием свойств действий алгебраического выражения.
Уметь применять правила раскрытие скобок.
Интеллектуальное мышление,
активность, любознательность, сообразительность, требовательность к себе. Формирование самостоятельных учебно-познавательных качеств.
Объяснение, иллюстрация, Работа с таблицами, по учебнику, устный опрос. Работа по индивидуальным карточкам.
Разбор формул, вывод обратных. Обработка правил, разбор схем решения, тест.
Таблицы: «Алгебраические и числовые выражения»,
«Формулы четного и нечетного числа», «Законы сложения и умножения», «Правила раскрытия скобок и заключения в скобки»
Презентация «Раскрытие скобок», электронный тест.
Работа по карточкам
Самостоятельная работа
1-2
Числовые выражения
2
Систематизировать и обобщить сведения о числовых выражениях, полученные учащимися в курсе математике 5-6 кл., сформировать понятие алгебраического выражения, систематизировать сведения о преобразовании алгебраического выражения.
Формировать алгебраические представления через запись законов и свойств арифметических действий с помощью букв, запись формул четного и нечётного чисел.
Сформировать понятие алгебраической суммы, обосновать правила раскрытия скобок свойствами сложения и вычитания, используя свойства действия, упростить алгебраическое выражение, найти числовое значение.
3
Алгебраические выражения
1
4-5
Алгебраические равенства. Формулы.
2
6-7
Свойства арифметических действий
2
8-10
Правила раскрытия скобок
2
11
Контрольная работа
II. Уравнения с одним неизвестным.
Понятие уравнения, корня уравнения, решения уравнения. Знать свойства уравнения.
Уметь применять свойства уравнения при решении. Уметь решать уравнения с одной переменной; решать несложные текстовые задачи с помощью составления уравнений.
Развитие познавательного интереса.
Самостоятельность
Объяснение, работа с книгой, работа по индивидуальным карточкам, устный опрос, тест
Таблица «Свойства уравнений».
Презентация, электронный тест.
Работа по карточкам
Самостоятельная работа
1-2
Уравнения и его корни
1
Систематизировать сведения о решении уравнений с одним неизвестным; сформировать умение решать уравнения, сводящиеся к линейным.
Сформировать представление об уравнениях как математическом аппарате решения разнообразных задач из математики, смежных областей знаний и практики.
Выработать умение решать текстовые задачи с помощью уравнений; решать линейные уравнения с одним неизвестным.
3-5
Решение линейных уравнений с одним неизвестным
3
6-8
Решение задач с помощью уравнений
4
9
Контрольная работа
III. Одночлены и многочлены.
Понятие степени, показателя степени, основания степени, одночлена, стандартного вида одночлена. Знать свойства степени с натуральным показателем, способ записи одночлена в стандартном виде, правило умножения одночленов.
Уметь находить значение степени, применять свойства степени с натуральным показателем для преобразования числовых и алгебраических выражений.
Уметь приводить одночлен к стандартному виду, выполнять умножение одночленов. Уметь объяснять действия и работать по алгоритму.
Понимать необходимость введения степени.
Значение одночлена в алгебре.
Умение самостоятельно выбирать способ решения.
Объяснение, работа с книгой, работа по карточкам, устный опрос.
Таблица «Свойства степени с натуральным показателем».
Презентация «Свойства степени с натуральным показателем»
Работа по карточкам
Самостоятельная работа
1-2
Степень с натуральным показателем
2
Освоить свойства степени с натуральным показателем. Сформировать понятие одночлена, стандартного вида одночлена.
Уметь применять свойства степени в действиях над одночленами.
3-4
Свойство степени с натуральным показателем
3
5
Одночлен. Стандартный вид одночлена
1
6-7
Умножение одночленов
3
8
Контрольная работа
9
Многочлен
2
Сформировать понятие многочлена, стандартного вида многочлена.
Выработать навыки приводить подобные слагаемые.
Выработать навыки сложения, вычитания многочленов.
Выработать умение проводить преобразование многочленов, умножение многочлена на одночлен и многочлен, а также деление многочлена на одночлен и многочлен, умение выполнять действия в комбинации.
Понятие подобных слагаемых, одночлена, многочлена, их стандартного вида, степень многочлена, суммы и разности многочленов. Знать правило умножения многочлена на одночлен и многочлен, правило деления многочлена на одночлен и многочлен.
Уметь называть члены многочлена, записывать многочлен в стандартном виде, находить сумму и разность многочлена, выполнят умножение, деление многочлена на одночлен и многочлен
Умение добиваться результата, формирование вычислительных навыков. Развивать сообразительность, активность, самостоятельность.
Объяснение, работа с книгой, работа по карточкам, устный опрос.
Схемы: «Приведение подобных слагаемых», «Сложение и вычитание многочленов» «Умножение многочлена на одночлен, многочлен», «Деление многочлена на одночлен, многочлен».
Презентация.
Работа по карточкам
Самостоятельная работа
10-11
Приведение подобных
1
12-13
Сложение и вычитание многочленов
2
14
Умножение многочлена на одночлен
2
15-16
Умножение многочлена на многочлен
3
17-18
Деление одночлена и многочлена на одночлен
2
19
Контрольная работа
IV. Разложение многочлена на множители.
Знать понятие разложение многочлена на множители, алгоритм разложения многочлена на множители способом группировки, знать формулу разности квадратов.
Знать устные формулировки формул квадрат суммы и квадрат разности.
Знать алгоритм поиска способов разложения многочлена на множители
Уметь выносить общий множитель за скобки, применять алгоритм разложения многочлена на множители группировки при решении упражнений, применять формулу разности квадратов при выполнении упражнений.
Уметь применять формулы
(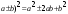
Уметь раскладывать многочлен на множители различными способами.
Понимать необходимость разложения многочлена на множители. Умение добиваться результата. Развивать сообразительность, активность, самостоятельность
Объяснение, работа с книгой, работа по карточкам, фронтальный опрос, устный опрос. Тест.
Схемы: «Вынесения общего множителя», «Способ группировки».
Таблица «Формулы сокращённого умножения» (квадрат разности, квадрат суммы, разность квадратов).
Презентация.
Работа по карточкам
Самостоятельная работа
1-2
Вынесение общего множителя за скобки
4
Выработать умение выполнять разложение многочлена на множители, уметь находить общий множитель, выносить общий множитель за скобки. Выработать умение применять формулы сокращённого умножения для преобразования алгебраический выражений. Усвоить формулы сокращенного умножения.
3-5
Способ группировки
3
6-8
Формула разности квадратов
3
9
Контрольная работа
10-11
12-13
Квадрат суммы
Квадрат разности
5
14-17
Способы разложения многочлена на множители
3
18
Контрольная работа №6
V. Алгебраические дроби.
Понятие алгебраической дроби, правило сокращения алгебраических дробей, приведение дробей к общему знаменателю, сложение и вычитание дробей, допустимое значение дроби. Алгоритм нахождения общего знаменателя, алгоритм сложения и вычитания дробей с разными знаменателями.
Формирование вычислительных навыков, умение работать по алгоритму. Уметь правильно выполнять сокращение дробей, приводить дроби к общему знаменателю, находить сумму и разность алгебраических дробей с разными знаменателями.
Развитие ценностных ориентаций, интеллектуального мышления.. Развивать умение самостоятельно выбирать способ решения.
Объяснение, работа с книгой, работа по карточкам, фронтальный опрос, устный опрос. Тест.
Таблица «Алгебраическая дробь». Схемы: «Сокращение дробей», «Приведение дробей к общему знаменателю», «сложение и вычитание дробей».
Работа по карточкам
Самостоятельная работа
1-4
Алгебраическая дробь. Сокращение дробей.
3
Сформировать понятие алгебраической дроби. Выработать умение преобразования алгебраических дробей, умение сокращать дроби, приводить к общему знаменателю, складывать и вычитать дроби. Сформировать умение пользоваться основным свойством дроби для решения упражнений.
5-7
Приведение дробей к общему знаменателю
3
8-11
Сложение и вычитание алгебраических дробей
5
12
Контрольная работа
13-16
Умножение и деление алгебраических дробей
4
Выработать умение умножать и делить дроби, проводить простейшие преобразования и выполнять совместные действия над алгебраическими дробями. Сформировать понятие допустимые значения алгебраической дроби.
Понятие произведения, частного. Знать правила выполнения действий умножения, деления и возведения в степень алгебраических дробей. Знать алгоритмы и правила по выполнению арифметических действий над алгебраическими дробями.
Уметь применять правила выполнения действий умножения, деления и возведения в степень алгебраических дробей, выполнять совместные арифметические действия над алгебраическими дробями. Выработать умение аргументировать действия, выполняемые над алгебраическими дробями.
Поиск рациональных путей решения, сообразительность. Умение добиваться результата.
Объяснение, работа с книгой, работа по карточкам, фронтальный опрос, устный опрос. Тест.
Схема «Умножение и деление алгебраических дробей»
Работа по карточкам
Самостоятельная работа
17-20
Совместные действия над алгебраическими дробями
5
21
Контрольная работа
VI. Линейная функция и её график.
Понятия прямоугольная система координат, абсцисса, ордината, координатные углы, графика функции, функция, функциональная зависимость, прямая пропорциональность, обратная пропорциональность, Знать различные способы задания функции, определение функции y=kx, её график и способы построения, определение линейной функции.
Уметь строить точку по её координатам и находить координаты любой точки координатной плоскости, находить значение функции заданной формулой, читать график функции, строить график функции y=kx, y=kx+b, при любых значениях k, b.
Умение оценивать и аргументировать. Сформировать мышление. Умение пользоваться чертежом для его исследования, найти нужную информацию. Правильное оформление результатов в работах.
Творческое, наглядное, рациональное мышление. Формирование интеллектуальных качеств: аккуратность, самостоятельность, логичность. Признание ценностей знаний.
Объяснение, работа с книгой, работа по карточкам, фронтальный опрос, устный опрос. Тест. Исследовательские задания, творческие задания.
Таблицы задания функции, график функции y=kx, y=kx+b.
Электронная презентация «Графики функции»
Практическая работа.
Самостоятельная работа
1-2
Прямоугольная система координат на плоскости
1
Сформировать представление о числовой функции на примере линейной функции. Сформировать понятие функции как математическая модель, позволяющая описывать и изучать разнообразные зависимости между реальными величинами. Сформировать умение переходить от одного языка функции к другому. Овладеть свойствами элементарной функции (линейная, прямая пропорциональность, обратная пропорциональность). Выработать умение строить их графики, исследовать расположение графиков на плоскости в зависимости от значений параметров, входящих в формулу.
3-4
Функция
2
5-7
Функция y=kx и его график
3
8-10
Линейная функция и её график
3
11
Контрольная работа
VII. Система двух линейных уравнений с двумя неизвестными.
1
Система уравнений
2
Научить учащихся решать системы двух линейных уравнений с двумя неизвестными аналитическими способами. Усвоить основную идею решения способом подстановки и сложения. Уметь применять на практике. Сформировать представление о графическом способе решения систем двух уравнений с двумя неизвестными. Выработать использовать данный метод. Выработать умение решать задачи с помощью систем уравнений известными способами. Научить учащихся видеть в условии две зависимые переменные для составления системы.
Понятие линейного уравнения с двумя неизвестными, систему двух линейных уравнений с двумя неизвестными, решение системы уравнения, график уравнения. Знать алгоритм решения системы линейных уравнений с двумя неизвестными способом подстановки, способом алгебраического сложения. Знать графический способ решения систему линейных уравнений, алгоритм составления системы уравнений по условию задачи с последующим соотнесением найденного решения системы с условием задачи.
Уметь находить пару чисел, удовлетворяющих системе уравнений, решать системы линейных уравнений с двумя неизвестными способом подстановки, алгебраического сложения. Уметь графически решать системы линейных уравнений, решать текстовые задачи с помощью систем уравнений с двумя неизвестными. Формирование вычислительных навыков, умение аргументировать и доказывать правильность суждения, умение работать по алгоритму. Находить рациональный способ решения. Формирование наглядно-образного мышления. Умение строить чертежи и читать их. Умение творчески и рационально подходить к решению поставленной задачи.
Формирование интеллектуальных качеств: аккуратность, самостоятельность, логичность. Поиск рациональных решений. Творческий подход к работе. Признание ценностей знаний.
Объяснение, иллюстрации, работа с книгой, работа по карточкам, фронтальный опрос, устный опрос. Индивидуальные разноуровневые задания.
Таблица «система двух линейных уравнений с двумя неизвестными», схемы решения систем различными способами. Презентация «Решение систем линейных уравнений»
Работа по карточкам
Самостоятельная работа
2-4
Способ подстановки
3+1 к.р
5-6
Способ сложения
3+1 к.р
7-8
Графический способ решения систем уравнений
2
9-11
Решение задач с помощью систем уравнений.
4
1
Самостоятельная работа
Комбинаторика
7
Итоговое повторение.