- Учителю
- Самостоятельные работы по алгебре 7 класс по учебнику Алимова
Самостоятельные работы по алгебре 7 класс по учебнику Алимова
Самостоятельная работа по теме «Алгебраические выражения»
Найдите значение данного выражения:
а) 8а - 11b, при а = -7, b = -3
б) 8m + 3n + 1, при m = - 6,5 и n = ![]()
в) (a + b)(a - b) , при а =1,7, b = -1,3
г) ![]() ,
при а = 2,8, b = 0
,
при а = 2,8, b = 0
Вариант II
Найдите значение данного выражения:
а) 3а - 15b, при а = -3 b = -7
б) 2m + 6n - 11, при m = - 3,5 и n = ![]()
в) (х - у)(х + у) , при х = - 1,3, у = 1,8
г) ![]() ,
при а = 0, b = 2,3
,
при а = 0, b = 2,3
Проверочная работа по теме «Формулы»
Стоимость междугородного разговора вычисляется по формуле А = аn, где А - общая стоимость разговора, а - стоимость 1минуты, n-количество минут.
а) Подсчитайте стоимость междугородного разговора, если a = 8,5 руб.,n = 4 мин.
б) Сколько минут длиться разговор, если
А = 84 руб., а = 7руб.?
в) Запищите формулу, по которой можно вычислить продолжительность разговора n.
Вариант II
Стоимость покупки вычисляется по формуле
С = cm, где С - стоимость покупки, с - цена 1 кг товара, m - масса товара.
а) Вычислите стоимость купленного сахара, если с = 30 руб., m = 3 кг.
б) Сколько килограммов сахара купили, если
С = 70 руб., с =14 руб.?
в) Запишите формулу, по которой можно вычислить массу покупки m.
Самостоятельная работа по теме «Раскрытие скобок»
Раскройте скобки и приведите подобные слагаемые:
1) 5х + (11 - 7х);
2) - (8с - 4) + 4;
3) (5 - 3b) + (3b - 11);
4) (5а - 36) - (2 + 5а -3b);
5) (1 - 9у) - (22у - 4) - 5;
6) (6х - 8) - 5х - (4 - 9х);
7) 5b - (6b + а) - (а - 6b);
8) 3 - 17а - 11(2а - 3);
9) а - (а - (2а - 4));
10)13b - (9b -((c - b) - 9b))
Вариант 2.
Раскройте скобки и приведите подобные слагаемые:
1) 6х + (7 - 3х);
2) - (4х - 18) + 18;
3) (2а - 7у) - (5а - 7у);
4) (11р + 9с) - (12 + 11р + 9с);
5) (2 - 4b) - (31b - 6) - 11;
6) (3а - 21) - 2а - (17 - 8а);
7) 14 b - (15b + у) - (у + 10 b);
8) 21х - 7 - 4 (9х + 3);
9) х - (х - (3х - 1)
10) 5с - (2с - ((b - с) - 2 b)).
Вариант 3
Раскройте скобки и приведите подобные слагаемые:
1) - 3q - (8p - 3q);
2) (2 + 3a) + (7a - 2);
3) - (11а + b) - (12а - 3b);
4) a + (a - 10) - (12 + a);
5) 3(8a - 4) + 6a;
6) 7p - 2(3p - 1);
7) - 4(3a + 2) + 8;
8) 7х - ((y - x) +3y);
9) 4y - (3y - (2y - (y + 1)))
10) 5с - (2с - ((b - с) - 2 b)).
Вариант 4
Раскройте скобки и приведите подобные слагаемые:
1) - 5b - (8a - 5b);
2) (5 - 2b) - (5 + 10b);
3) - (3c + 5x) - (9c - 6x);
4) x + (x - 15) + (13 + x);
5) 7(5a + 8) - 11a;
6) 33a - 8(4a - 1);
7) - 2(2p + 2) + 4;
8) 12y - ((x - y) + 12x);
9) 5a - (6a - (7a - (8a - 9)))
10) 13b - (9b -((c - b) - 9b))
Контрольная работа по теме «Алгебраические выражения»
1. Вычислить:
43 ∙ 0,12 - ![]() ∙
32 + 2,5
∙
32 + 2,5
2. Найти значение алгебраического выражения:
5(3х - 7) - 4(21 + 7х); если х = ![]()
3. Упростить выражение:
а) 35х - (16у - 17х) + 27у
б) 56а - 27k + (12a - 15k)
в) 15а - 3(14,5а - 27) + 15,2
4. Решите задачу:
Турист шел пешком 9 км., ехал на автобусе t ч. со скоростью 43 км/ч, плыл по озеру на лодке
2 ч, скорость которой V км/ч. Найдите путь, проделанный туристом, если t =3,2 ч, V=21,4км/ч
Вариант 2.
1. Вычислить:
![]() ∙
81 - 2,4 ∙ 0,65 - 7,9
∙
81 - 2,4 ∙ 0,65 - 7,9
2. Найти значение алгебраического выражения:
6(8а + 12) + 4(25 - 3а); если а = - ![]()
3. Упростить выражение:
а) 18а + (24b - 13a) - 43b
б) 16x - 85b - (42x - 24b)
в) 13,7 +4(- 2,8x - 32,4) - 18x
4. Решите задачу:
Турист ехал на автобусе 2,7 ч. со скоростью
V км/ч., шел пешком 8 км., а затем t ч. плыл по озеру на катере, скорость которого 19,6 км/ч. Найдите путь, проделанный туристом, если
V = 52 км/ч., t = 3,4 ч.
Вариант 3.
1. Вычислите:
![]() ;
;
2. Упростите выражение 5(3 - х) + 7 (2х - 3) и найдите его числовое значение при х = - 0,6.
3. Раскройте скобки и упростите:
а) 18а + (24b - 13a) - 43b
б) 16x - 85b - (42x - 24b)
в) 3а - (6а - (2а - 1))
4. Турист планировал пройти расстояние S км
за t ч, но преодолел его на 2 ч быстрее. Запишите формулу скорости, с которой шел турист. Вычисли скорость туриста, если S=32 км, t = 10ч.
Вариант 4.
1. Вычислите:
![]()
2. Упростите выражение 3(5х - 7) + 8 (2 - х) и найдите числовое значение при х = - 0,7.
3. Раскройте скобки и упростите:
а) 35х - (16у - 17х) + 27у
б) 56а - 27k + (12a - 15k)
в) - (5b - (2 - 3b)) + 7b.
4. Турист планировал пройти расстояние S км
за t ч, но преодолел его на 1 ч быстрее. Запишите формулу скорости, с которой шел турист. Вычисли скорость туриста, если S = 35 км, t = 9ч.
Самостоятельная работа по теме «Решение уравнений»
Решите уравнение
-
7х - 4 = х - 16;
-
13 - 5х = 8 - 2х;
-
5х + (3х - 7) = 9;
-
(7х + 1) - (6х + 3) = 5;
-
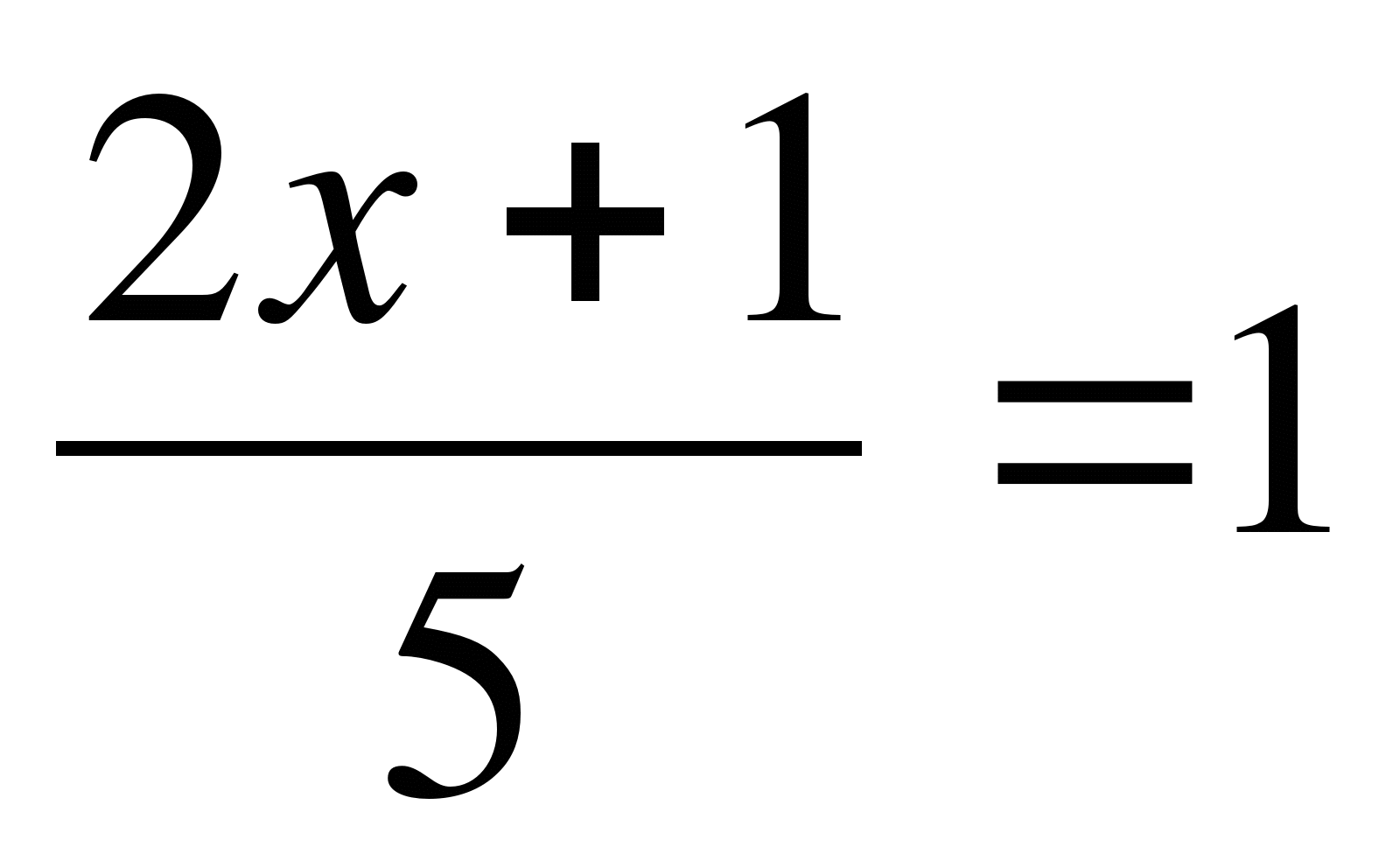
Вариант I
Решите уравнение
-
7х - 4 = х - 16;
-
13 - 5х = 8 - 2х;
-
5х + (3х - 7) = 9;
-
(7х + 1) - (6х + 3) = 5;
-
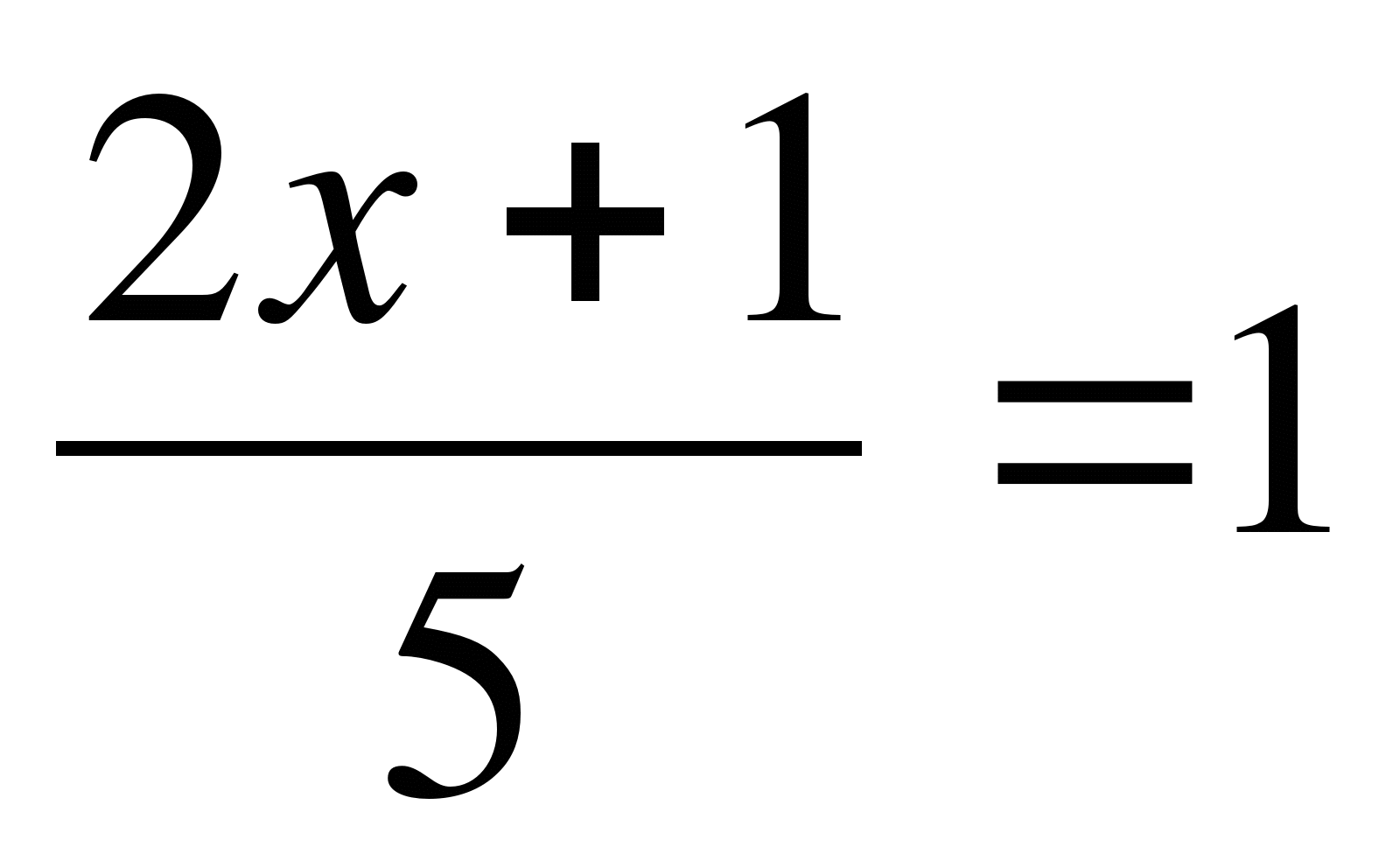
Вариант II
Решите уравнение
-
19 - 5 (3х - 1) = 9;
-
(4х + 3) - (10х + 11) = 7 + (13 - 4х);
-
30 + 5 (3х - 1) = 35х - 25;
-
6х - 5 (3х + 2) = 5 (х - 1) - 8;
-
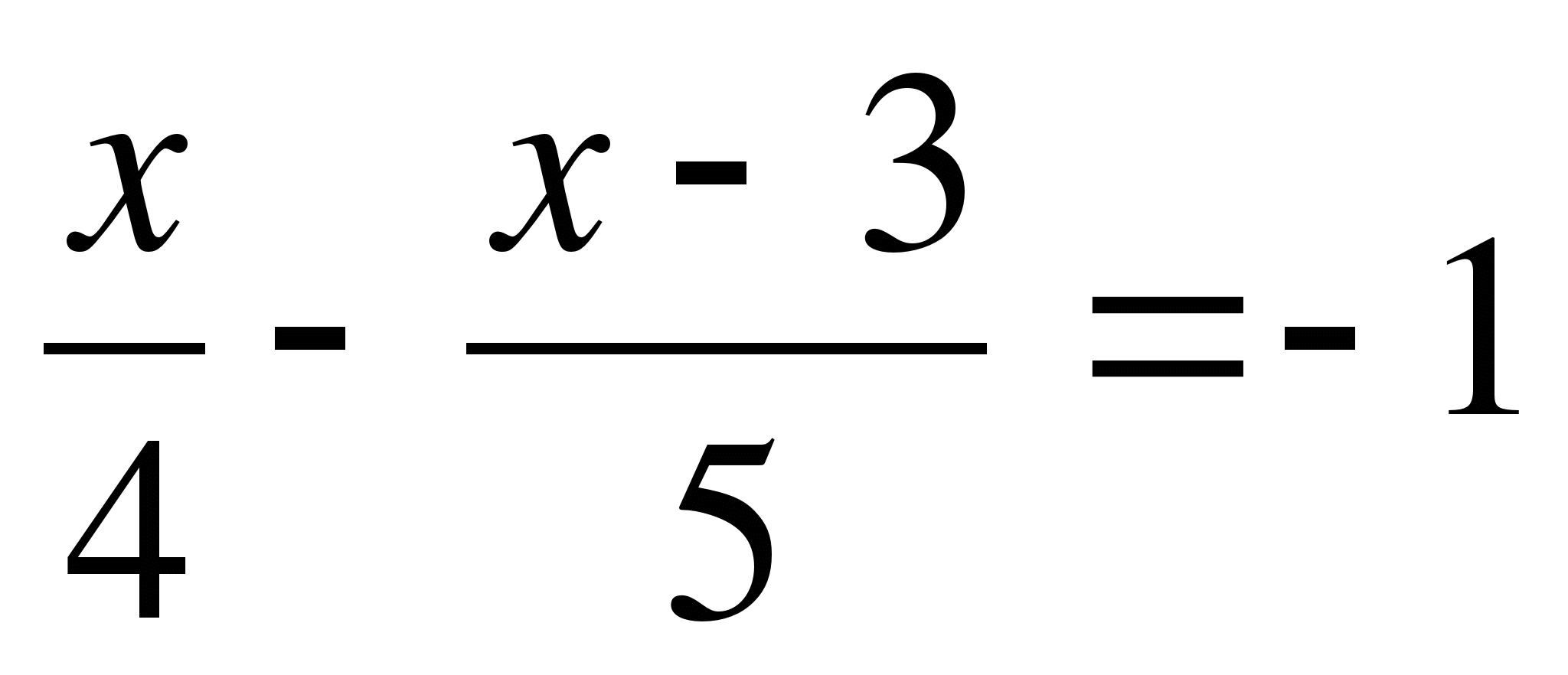
Вариант II
Решите уравнение
-
19 - 5 (3х - 1) = 9;
-
(4х + 3) - (10х + 11) = 7 + (13 - 4х);
-
30 + 5 (3х - 1) = 35х - 25;
-
6х - 5 (3х + 2) = 5 (х - 1) - 8;
-
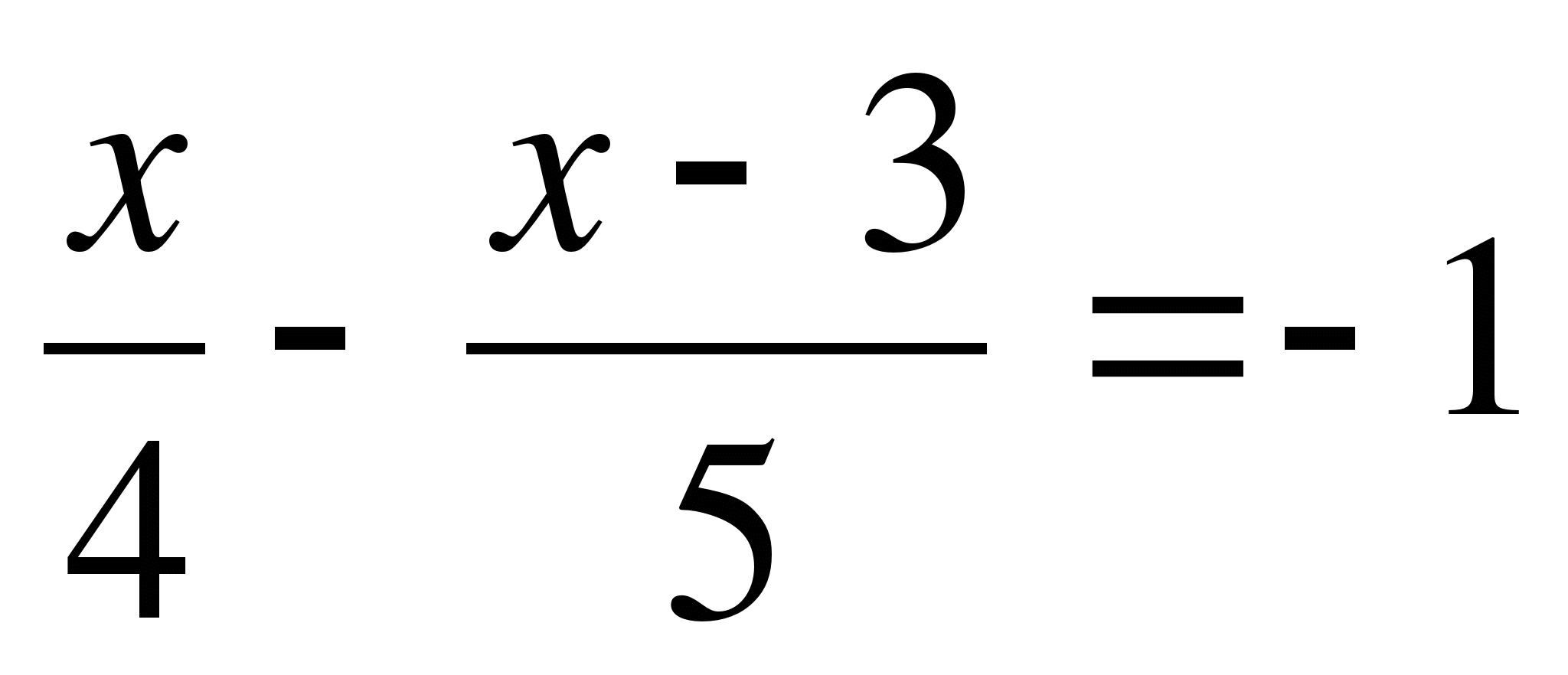
Вариант III
Решите уравнение
-
(7 - 5х) - (8 - 4х) + (5х + 6) = 8;
-
20 + 4 (2х - 5) = 14х + 12;
-
4 (2 - 3х) + 7 (6х + 1) - 9 (9х + 4) = 30;
-
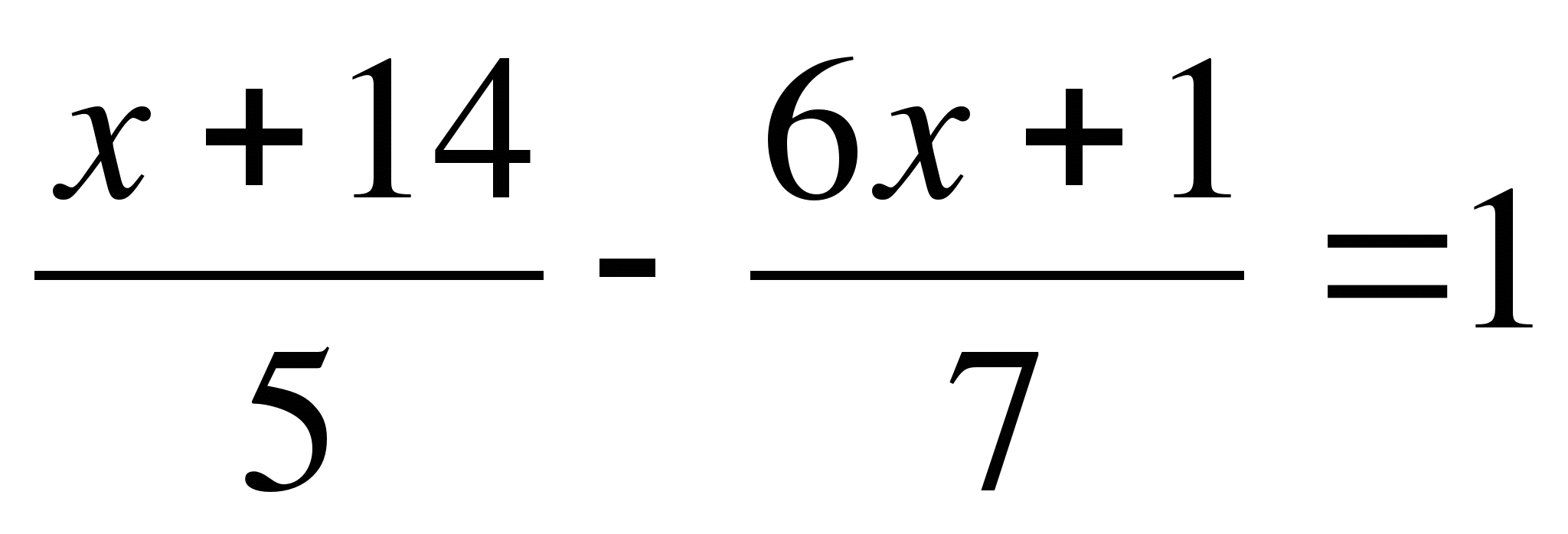 ;
;
-
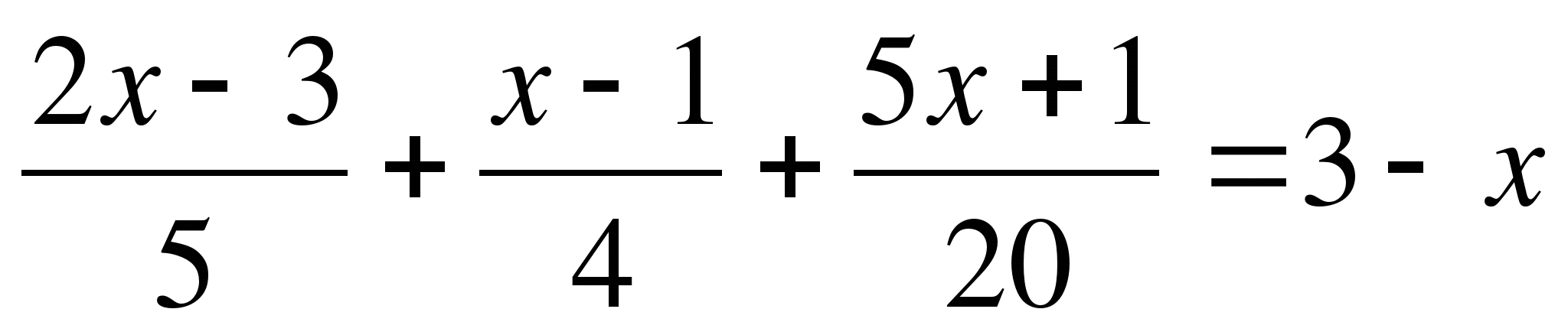
Вариант III
Решите уравнение
-
(7 - 5х) - (8 - 4х) + (5х + 6) = 8;
-
20 + 4 (2х - 5) = 14х + 12;
-
4 (2 - 3х) + 7 (6х + 1) - 9 (9х + 4) = 30;
-
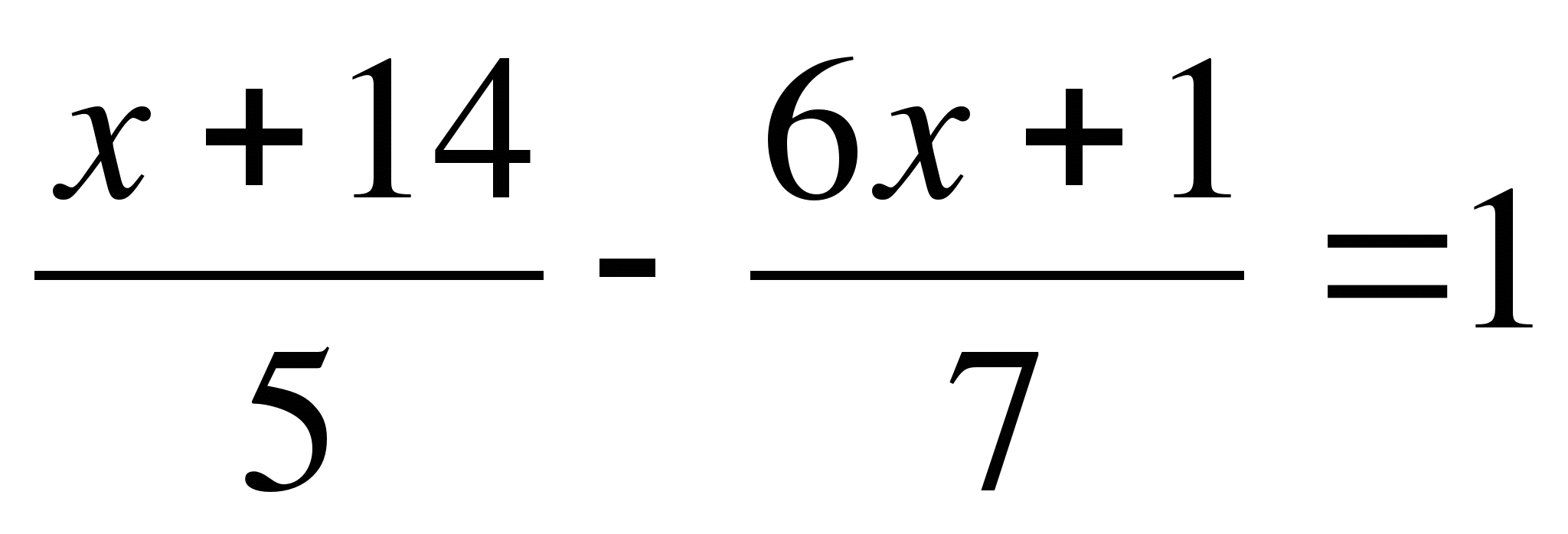 ;
;
-
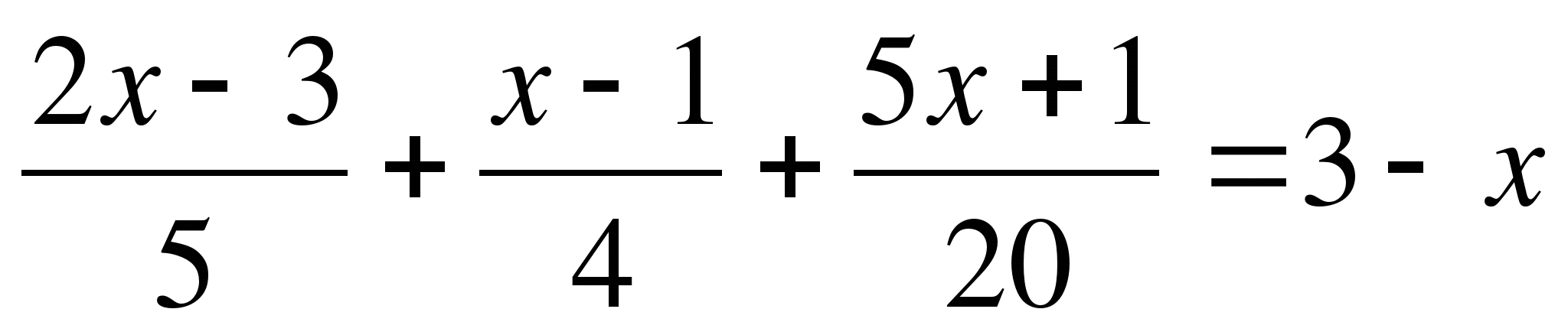
Решите уравнение
1) 7х - 4 = х - 16;
2) 13 - 5х = 8 - 2х;
3) 5х + (3х - 7) = 9;
4) (7х + 1) - (6х + 3) = 5;
5) ![]()
Вариант I
Решите уравнение
-
7х - 4 = х - 16;
-
13 - 5х = 8 - 2х;
-
5х + (3х - 7) = 9;
-
(7х + 1) - (6х + 3) = 5;
-
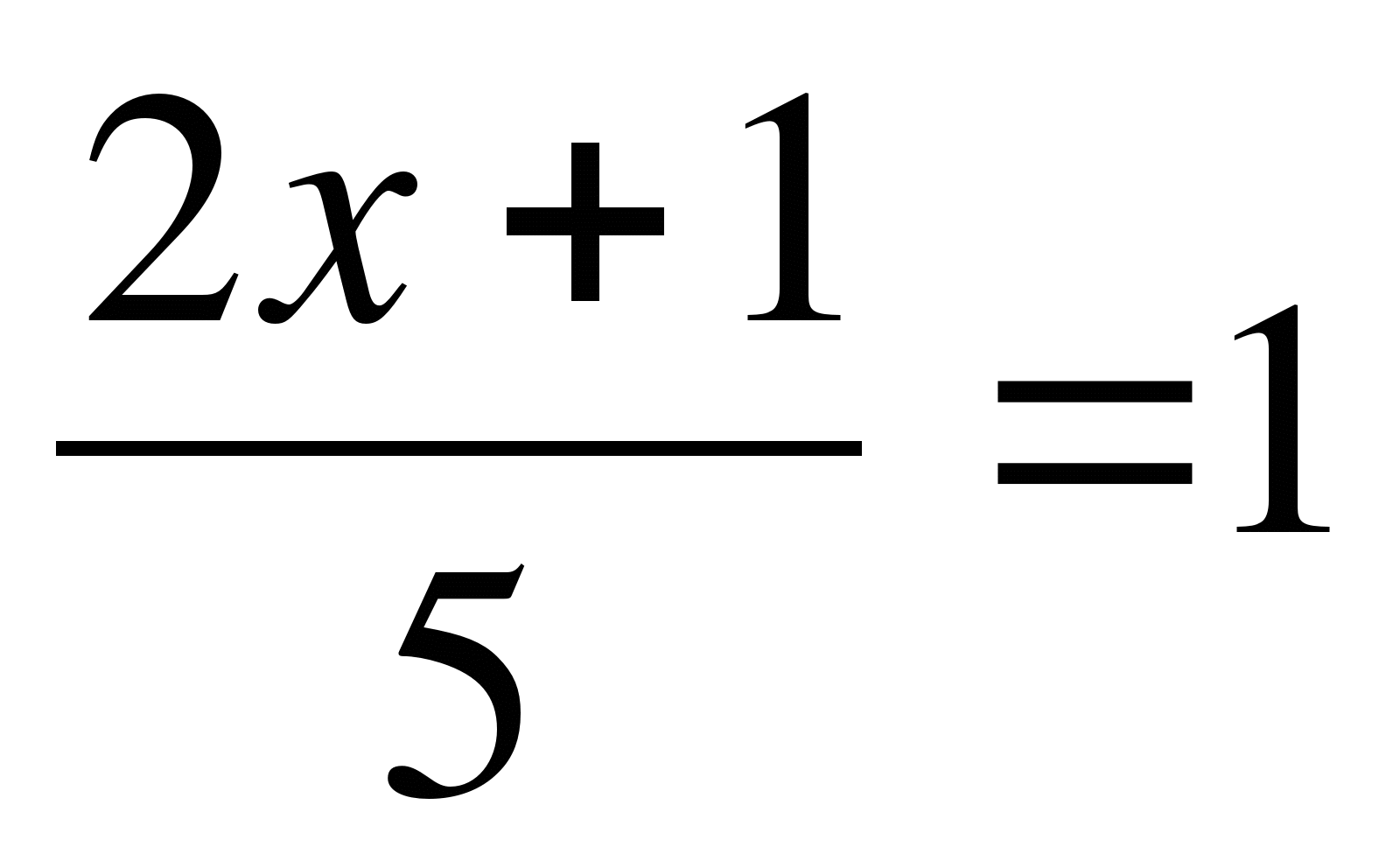
Вариант II
Решите уравнение
1) 19 - 5 (3х - 1) = 9;
2) (4х + 3) - (10х + 11) = 7 + (13 - 4х);
3) 30 + 5 (3х - 1) = 35х - 25;
4) 6х - 5 (3х + 2) = 5 (х - 1) - 8;
5) ![]()
Вариант II
Решите уравнение
-
19 - 5 (3х - 1) = 9;
-
(4х + 3) - (10х + 11) = 7 + (13 - 4х);
-
30 + 5 (3х - 1) = 35х - 25;
-
6х - 5 (3х + 2) = 5 (х - 1) - 8;
-
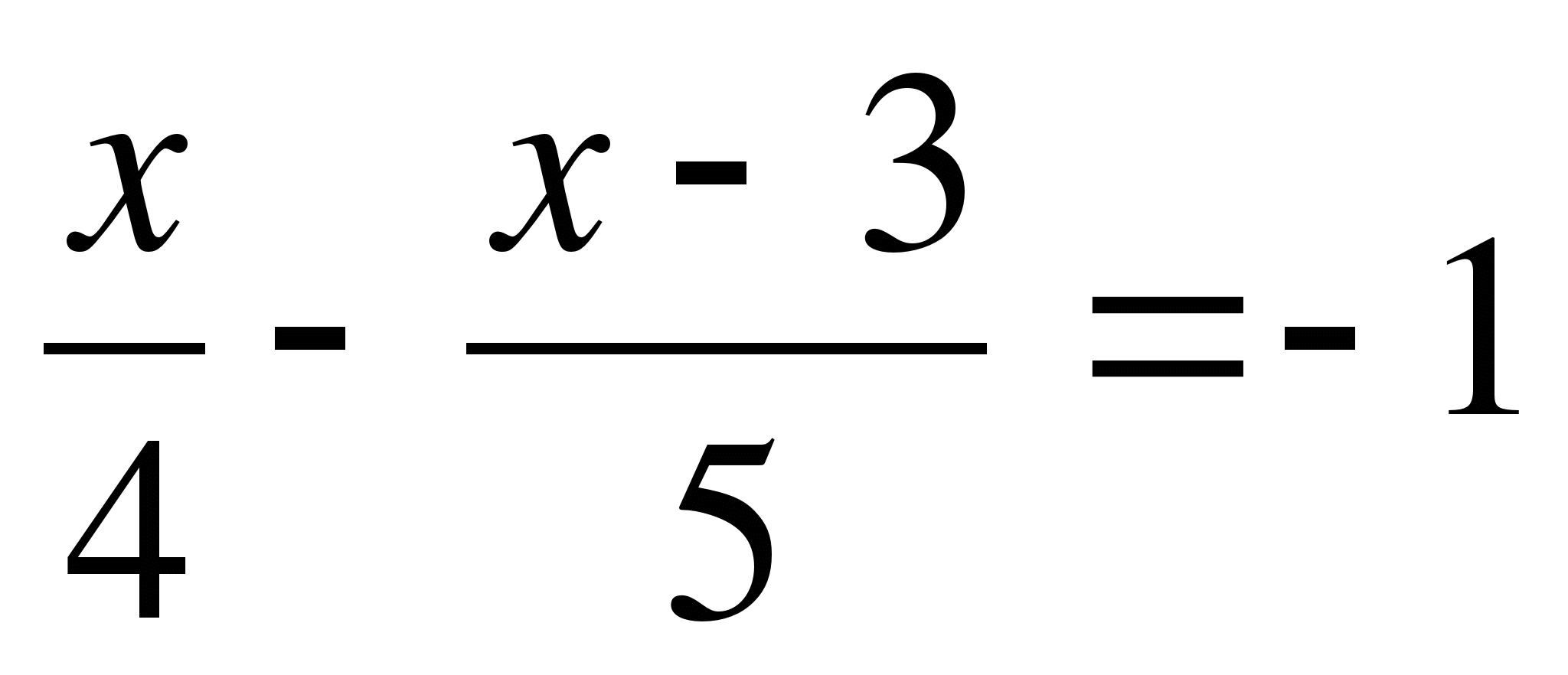
Вариант III
Решите уравнение
1) (7 - 5х) - (8 - 4х) + (5х + 6) = 8;
2) 20 + 4 (2х - 5) = 14х + 12;
3) 4 (2 - 3х) + 7 (6х + 1) - 9 (9х + 4) = 30;
4) ![]() ;
;
5) ![]()
Вариант III
Решите уравнение
-
(7 - 5х) - (8 - 4х) + (5х + 6) = 8;
-
20 + 4 (2х - 5) = 14х + 12;
-
4 (2 - 3х) + 7 (6х + 1) - 9 (9х + 4) = 30;
-
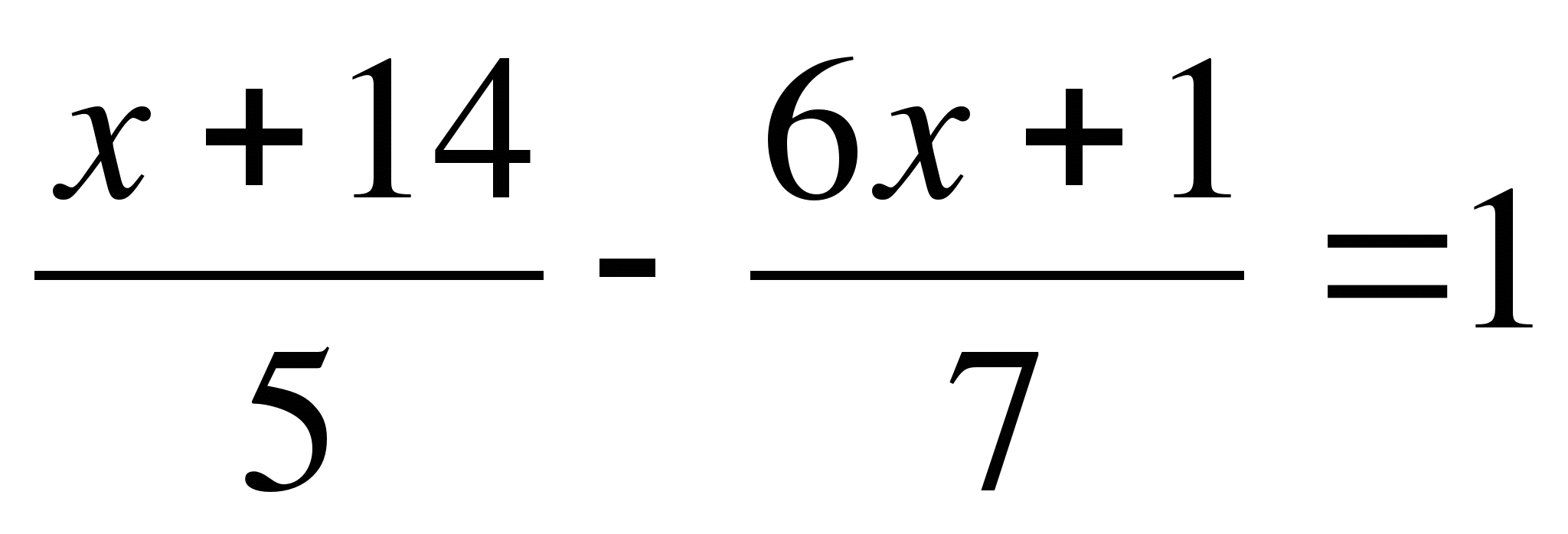 ;
;
-
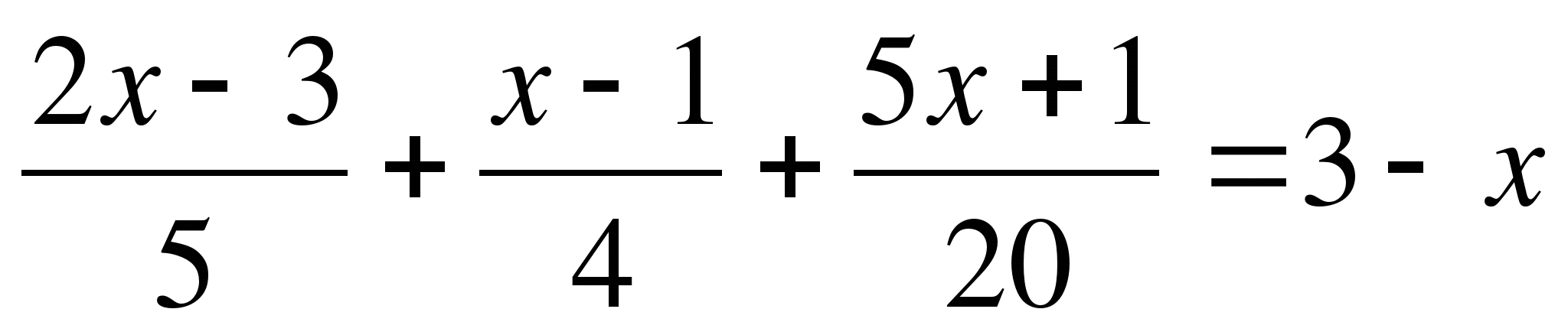
Самостоятельная работа по теме «Решение задач с помощью уравнений»
1) Папе и дедушке вместе 111 лет. Сколько лет каждому, если папа в 2 раза моложе дедушки?
2) За 3 ч мотоциклист проезжает то же расстояние, что велосипедист за 5 ч. Скорость мотоциклиста на 12 км/ч больше скорости велосипедист. Определите скорость каждого.
Вариант 2
1) Двое рабочих изготовили 657 деталей, причем первый изготовил на 63 детали больше второго. Сколько деталей изготовил каждый?
2) Стоимость изделия третьего сорта в 3 раза меньше стоимости первого сорта. Сколько стоит каждое изделие, если изделие первого сорта стоит на 50 р. дороже изделия третьего сорта?
Вариант 3
1) В двух седьмых классах 67 учеников, причем в одном на 3 ученика больше, чем в другом. Сколько учеников в каждом классе?
2) За 2 ч грузовик проезжает на 20 км больше, чем легковой автомобиль за 1 ч. Скорость легкового автомобиля в 1,5 раза больше скорости грузовика. Определите скорость каждого.
Вариант 4
1) У Коли и Пете вместе 98 марок, причем у Коли в 6 раз больше марок, чем у Пети. Сколько марок у каждого?
2) Мама весит в 5 раз больше дочери, а дочь весит на 40 кг меньше мамы. Сколько весят мама и дочь в отдельности?
Вариант 5.
1) Мастер изготовляет на 8 деталей в час больше, чем ученик. Ученик работал 6 ч, а мастер 8 ч, и вместе они изготовили 232 детали. Сколько деталей в час изготовлял ученик?
2) На путь от поселка до станции автомобиль потратил на 1 ч меньше, чем велосипедист. Найдите расстояние от поселка до станции, если автомобиль проехал его со скоростью 60 км/ч, а велосипедист 20 км/ч.
Вариант 6.
1) Из двух пунктов, расстояние между которыми 240 км, навстречу друг другу выехали автомобиль и мотоциклист. Скорость автомобиля на 30 км/ч больше скорости мотоцикла. Найдите скорость автомобиля и скорость мотоцикла, если известно, что автомобиль был в пути 3 ч, а мотоцикл 2 ч.
2) В столовую привезли картофель, упакованный в пакеты по 3 кг. Если бы он был упакован в пакеты по 5 кг, то понадобилось бы на 8 пакетов меньше. Сколько килограммов картофеля привезли в столовую?
Контрольная работа по теме «Уравнения и его корни»
1. Решите уравнение:
а) 3х + 2,7 = 0; б) 2х + 7 = 3х - 2(3х - 1);
в) ![]()
2. Решите задачу:
В трех седьмых классах 103 ученика. В VII Б на 4 ученика больше, чем в VII А, и на 2 ученика меньше, чем в VII В. Сколько учеников в каждом классе?
3. При каком значении х значения выражений
![]() равны?
равны?
4. Решите задачу:
Лодка шла по течению реки 2,4 часа, а против течения реки 4,5 часа. Найти собственную скорость лодки, если она прошла всего 78,57 км., а скорость течения реки 3 км/ч.
Вариант 2.
1. Решите уравнение:
а) 4,8 - 2х = 0; б) 4 - 2(х + 3) = 4(х - 5);
в) ![]()
2. Решите задачу:
В магазин привезли 309 тетрадей. В клетку на 13 тетрадей меньше, чем общих тетрадей и в 6 раз меньше, чем в линейку. Сколько тетрадей каждого сорта привезли в магазин?
3. При каком значении х значения выражений
![]() равны?
равны?
4. Решите задачу:
Лодка шла по течению реки 2,4 часа, а против течения реки 4,5 часа. Найти собственную скорость лодки, если она прошла всего 78,57 км., а скорость течения реки 3 км/ч.
1. Вычислить:
25 + 17 - 364
2. Упростить:
а ∙ а ∙ а + а ∙ а ∙ а - b ∙ b ∙ b ∙ b
3. Записать число в виде суммы разрядных слагаемых: 57891
4. Записать число в стандартном виде: 35890; 542,16
Вариант 2
1. Вычислить:
43 - 50 + 428 - 54
2. Упростить:
а ∙ а ∙ а ∙ а + с ∙ с ∙ с ∙ с ∙ с + с ∙ с ∙ с ∙ с ∙ с - а ∙ а ∙ а ∙ а + а ∙ а ∙ а ∙ а
3. Записать число в виде суммы разрядных слагаемых: 5007920
4. Записать число в стандартном виде:
478900; 3621,37
Вариант 3
1. Вычислить:
![]()
2. Упростить:
![]()
3.Записать число в виде суммы разрядных слагаемых:
800700639000
4. Записать число в стандартном виде:
5890372,105; 254,6 миллиона
Самостоятельная работа по теме «Свойства степеней»
1. Упростите выражение:
а) с7∙с4; б) b ∙ b2 ∙ b3 в) х8 : х4;
г) с6 : с; д) (аb)9; е) (2ас)4;
ж) ![]() ;
з) х15 : х5 ∙ х; и) а4 ∙
(а7)5; к)(у ∙ у2)3 : (у
∙ у3)2.
;
з) х15 : х5 ∙ х; и) а4 ∙
(а7)5; к)(у ∙ у2)3 : (у
∙ у3)2.
2. Вычислите:
а) 211 : 25; б) ![]() ;
в) 37 ∙ (32)3 : 310;
;
в) 37 ∙ (32)3 : 310;
г) ![]() ;
д)
;
д) ![]() .
.
3. Замените * таким выражением, чтобы выполнялось равенство:
а) (а ∙ а4)2 : * = а2; б) (а3)2 ∙ * = - а24; в) а6 ∙ (а ∙ а2)2 = * ∙( - а4)
Вариант 2.
1. Упростите выражение:
а) х8∙х3; б) а3 ∙ а2 ∙ а; в) у10 : у4;
г) с6 : с5; д) (bс)6; е) (3ху)3;
ж) ![]() ;
з) х8 ∙ х3 : х5; и)
(х3)2 ∙ х4; к)( у3 ∙
у)3 ∙ (у3 ∙ у)2.
;
з) х8 ∙ х3 : х5; и)
(х3)2 ∙ х4; к)( у3 ∙
у)3 ∙ (у3 ∙ у)2.
2. Вычислите:
а) 617 : 614; б) ![]() ;
в) 28 ∙ (23)2 : 212;
;
в) 28 ∙ (23)2 : 212;
г) ![]() ;
д)
;
д) ![]() .
.
3. Замените * таким выражением, чтобы выполнялось равенство:
а) (х3 ∙ х)3 : * = х6; б) (х4)3 ∙ * = - х15; в) (х3∙ х2)2 = * ∙( - х) 3
Самостоятельная работа по теме «Одночлены»
1. Приведите одночлен к стандартному виду:
а) 4ab3a2bc; б) ![]() cdb46c2d3;
в)-
cdb46c2d3;
в)-![]() a3k2
a3k2![]() a2k8b
a2k8b
2. Запишите одночлен в стандартном виде и найдите его числовое значение:
36ас![]() а,
если а = -
а,
если а = - ![]() , с
= 12;
, с
= 12;
а = - ![]() , с
= - 50.
, с
= - 50.
Вариант 2.
1. Приведите одночлен к стандартному виду:
а)![]() ak24b3a6;
б)5ab416a3bc2;
ak24b3a6;
б)5ab416a3bc2;
в)![]() c2b3
t
c2b3
t![]() c4b5
c4b5
2. Запишите одночлен в стандартном виде и найдите его числовое значение:
45bс![]() b,
если b = -
b,
если b = - ![]() , с
= 36;
, с
= 36;
b = - ![]() , с
= - 96.
, с
= - 96.
Самостоятельная работа
«СЛОЖЕНИЕ И ВЫЧИТАНИЕ МНОГОЧЛЕНОВ» (1)
Вариант 1
1. (7х2 - 5х + 3) - (7х2 - 5)
2. (3х + 1) + ( - 3х2 - 3х + 1)
3. (а + 3b) + (3a - 3b)
4. a2 - 5ab - b2 - (a2 + b2)
5. (x + y - z) - (x - y) + (x - y + z)
Вариант 2
1. (3a2+ 7a - 5) - (3a2+ 1)
2. (5a + 3) + ( - 2a2 - 5a + 7)
3. x2 - 3xy + y2 - (x2 - y2)
4. (x + 6y) + (3x - 6y)
5. (a - b + c) + (a - c) - (a - b - c)
Контрольная работа по теме «Одночлены и многочлены»
Вариант 1.
1. Представьте выражение в виде степени:
а) 64 · 65; б) 312 : 34; в) (78)2;
г) 43 · 23; д) (35)2 · (42)5.
2. Упростите выражение:
а) (16b + k2 - 4d) - (k2 + 6d);
б) a + b - (a - 2b) + (a + 3b) + (a + 4b) - (a - 5b).
3. Выполните действия:
а) (- 2u2 + 3u + 1) (- 4u);
б) (32c2d5+ 60c6d2 - 44d4c3) : (4с2d2);
в) (y2 + 2y + 2)(y2 - 2y + 2);
г) (a + b)(a - b)(a2 + b2).
4. Упростите и найдите значение выражения: 4m2(m - 2) - (2m2 - 6)(2m + 6) + 12m2;
если m = - 1,5
5. Решите уравнение:
а) (- 5)2х + (0,5)2 = (- 1)9 - (3 - 15х).
Вариант 2.
1. Представьте выражение в виде степени:
а) 72 · 73; б) 510 : 53; в) (62)4;
г) 52 · 72; д) (83)4 · (24)3.
2. Упростите выражение:
а) (15с + а2 - 3k) - (a2 - 6c);
б) a + k - (a - 2k) + (a + 3k) - (a + 6k) + (a - 7k).
3. Выполните действия:
а) (- 4x3 - 3x2 + 12x) (- 6x);
б) (45a3b8+ 60a7b3 - 75b4a5) : (15a3b3);
в) (3z2 - 2z + 1)(3z2 + 2z + 1);
г) (c + d)(c2 + d2)(c - d).
4. Упростите и найдите значение выражения: 6m2(m - 4) - (3m2 - 5)(2m + 5) + 24m2;
если m = - 2,5
5. Решите уравнение:
а) (- 4)2х + (0,7)2 = (- 1)7 - (8 - 6х).
Вариант 3.
1. Представьте выражение в виде степени:
а) 43 · 45; б) 726 : 714; в) (55)3;
г) 94 · 24; д) (82)3 · (42)2.
2. Упростите выражение:
а) (2у2 + 8у - 11) - (3у2 - 6у + 3);
б) (8с2 + 3с) + ( - 7с2 - 11с + 3) - (- 3с2 - 4).
3. Выполните действия:
а) 2a(2а2 - 8аb + b2);
б) (20c3d8+ 50c6d4 - 55d7c5) : (5с3d4);
в) (y + 2y2 + 3)(y2 - 2y + 2);
4. Упростите и найдите значение выражения:
(2x - y)(2x + y) + (y - 0,5x)(y + 0,5x)
если x = 0,4, y = 1,7
5. Решите уравнение:
а) 3a(a - 7) - a(4 + 3a) = 5
Вариант 3.
1. Представьте выражение в виде степени:
а) 43 · 45; б) 726 : 714; в) (55)3;
г) 94 · 24; д) (82)3 · (42)2.
2. Упростите выражение:
а) (2у2 + 8у - 11) - (3у2 - 6у + 3);
б) (8с2 + 3с) + ( - 7с2 - 11с + 3) - (- 3с2 - 4).
3. Выполните действия:
а) 2a(2а2 - 8аb + b2);
б) (20c3d8+ 50c6d4 - 55d7c5) : (5с3d4);
в) (y + 2y2 + 3)(y2 - 2y + 2);
4. Упростите и найдите значение выражения:
(2x - y)(2x + y) + (y - 0,5x)(y + 0,5x)
если x = 0,4, y = 1,7
5. Решите уравнение:
а) 3a(a - 7) - a(4 + 3a) = 5
ВЫНЕСЕНИЕ ОБЩЕГО МНОЖИТЕЛЯ ЗА СКОБКИ
1. Вынесите общий множитель за скобки:
а) 2х + 3хy; б) 5ab+10a2;
в) ху3 + 5х2у2 - 3х2у .
2. Разложите на множители:
а) у(а + с) + х (а + с);
б) х(а + с) - х(а + с);
в) a(b - c) + c(c - b);
г) (х - 2)(8b + 1) - (7b - 3)(2 - х).
Вариант 3.
1. Вынесите общий множитель за скобки:
а) 2аb - 10b; б) 3а3b - 6а2b2;
в) 14х3 у5 + 21х6у2 - 7х3у2.
2.Разложите на множители:
а) хd(аg + сb) + хd(аf -bс);
б) 2х(m - n) - (n - m);
в) (у + x)(а + с)2 + (х + m)(а + с)2;
г) (3х - 1)(8b + 1) + (7b - 3)(1 - 3х).
Вариант 2.
1. Вынесите общий множитель за скобки:
а) 3ху - 5у; б) 7аb - 14а2;
в) 3 а3с2 +6а2с3 - 9а3с3.
2. Разложите на множители:
а) a(b + c) + x(b + c);
б) а(х + у) + a(b - x);
в) k(x - y) + c(y - x);
г) (а - b)(5а + 11) - (3а - 11)(b - а).
Вариант 4.
1. Вынесите общий множитель за скобки:
а) 8р + 2рс; б)8х4у2 - 12x2у2;
в) 12а4с5 + 36а8с5 - 48а4с15.
2. Разложите на множители:
а) аk(fх + mу) + ak(yb - xf);
б) 3p (a - c) - (c - a);
в) (n - a)(b + c)3 + (n + x)(b + c)3;
г) (2а - b)(3а + 11) + (5а - 18)(b - 2а).
Самостоятельная работа по теме «Разложение на множители способом группировки»
1. Разложите на множители
1) p(x + y) - x - y +7px + 7py
2) 6ma - 12m - 3a + 6
3) x3 + x - 3xy +2 + 2x2 - 6y
4) m3n2 - 4mn2 + 4m - m3
5) (x - 2)2 - 4(2 - x)(x + 3)
6) ba - 4a - 2b - 8
7) 2mx + m - 6x - 3
2. Вычислите:
0,1 · 15,3 + 0,1 · 10,7 + 9,9 · 15,3 + 9,9 · 10,7
Вариант 1.
1. Разложите на множители
1) ac + ad + 2bc + 2bd
2) x2 + xy - xz - yz
3) 5x - 10x2 - 4 + 8x
4) a(6 - a) - (6 - a)
5) b(a + b) + a + b
6) ba - 4a - 2b - 8
7) 2mx + m - 6x - 3
2. Вычислите:
127 · 64 + 173 · 64 + 127 · 36 + 173 · 36
Вариант 1.
1. Разложите на множители
1) ac + ad + 2bc + 2bd
2) x2 + xy - xz - yz
3) 5x - 10x2 - 4 + 8x
4) a(6 - a) - (6 - a)
5) b(a + b) + a + b
6) ba - 4a - 2b - 8
7) 2mx + m - 6x - 3
2. Вычислите:
127 · 64 + 173 · 64 + 127 · 36 + 173 · 36
Вариант 2.
1. Разложите на множители
1) x2у - z2x + y2x - z2y
2) y4 + 3 - y2 - 3y2
3) p(a + b) - a - b
4) 2ax2 - 6a + x2 - 3
5) c(x + y) + 7cx + 7cy
6) 64x3 - 8x2 - 2 + 16х
7) a2 (a - 5) - 2a + 10
2. Вычислите:
10,7 · 34 - 11,3 · 24 + 11,3 · 34 - 10,7 · 24
Самостоятельная работа по теме «Формула разности квадратов»
1. Разложите на множители
1) m2 - a2; 2) 4х2 - 9;
3) ![]() -
х2; 4) 81х2 -
25у2.
-
х2; 4) 81х2 -
25у2.
2. Выполни умножение:
1) (а + 2)(а - 2); 2) (c - p)(c + p);
3) (5b + 6)(5b - 6); 4) (7 -![]() а)
(7 +
а)
(7 +![]() а).
а).
Вариант 2.
1. Разложите на множители
1) 16х2 - 25; 2) k6 - 1;
3) ![]() c2
-
c2
- ![]() ;
4) 144a6 - 121b4.
;
4) 144a6 - 121b4.
2. Выполни умножение:
1) (3x + y)(3x - y); 2) (5c - 2a)(5c + 2a);
3) (6x2 + 2y3)(6x2 - 2y3);
4) (![]() )(
)(![]() ).
).
Вариант 3.
1. Разложите на множители
1)0,09х4у2 - 0,36z2; 2) 36х18 - 25у4;
3) ![]() ;
4) (2а + b)2 - 4a2.
;
4) (2а + b)2 - 4a2.
2. Выполни умножение:
1) 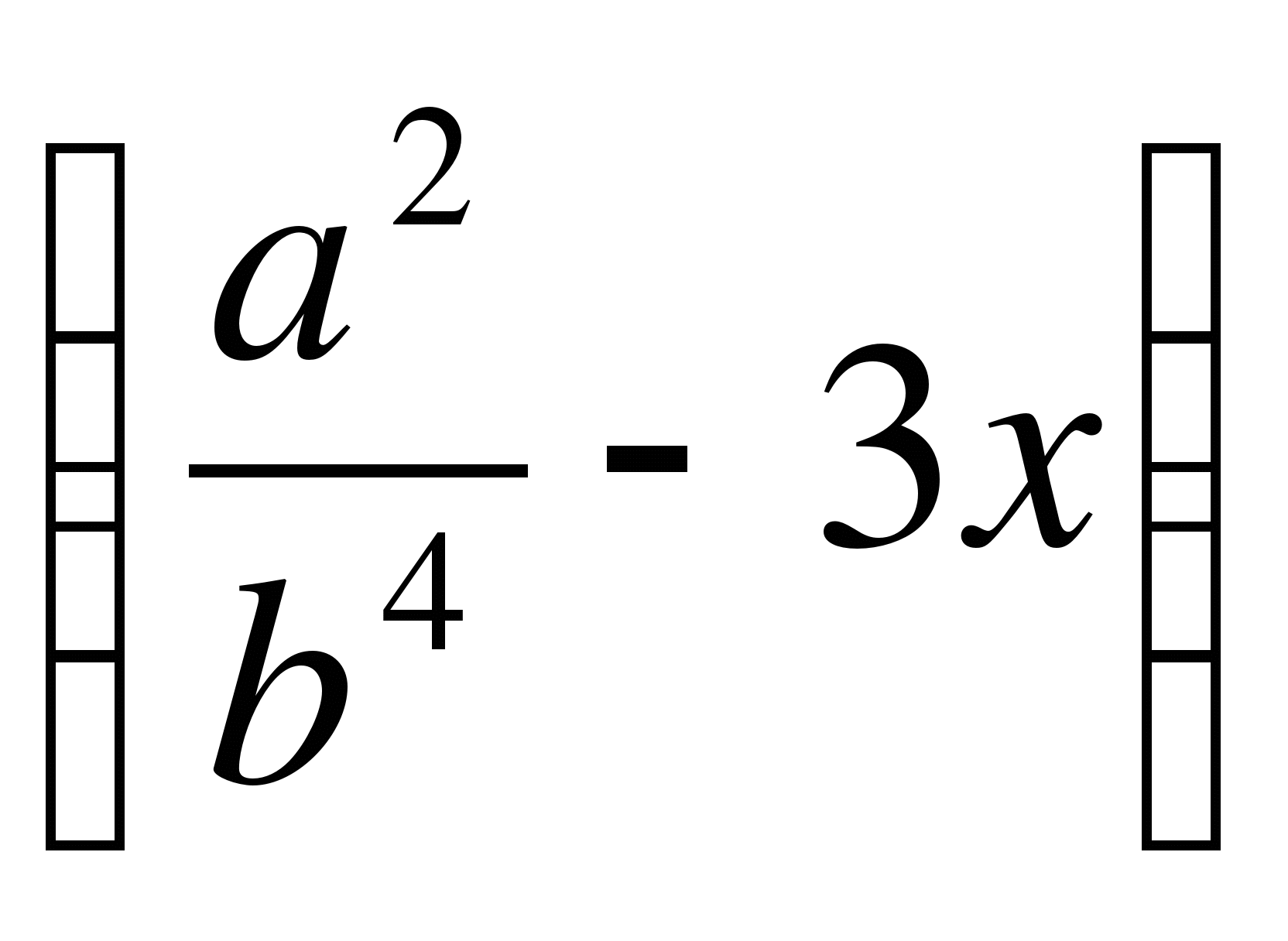
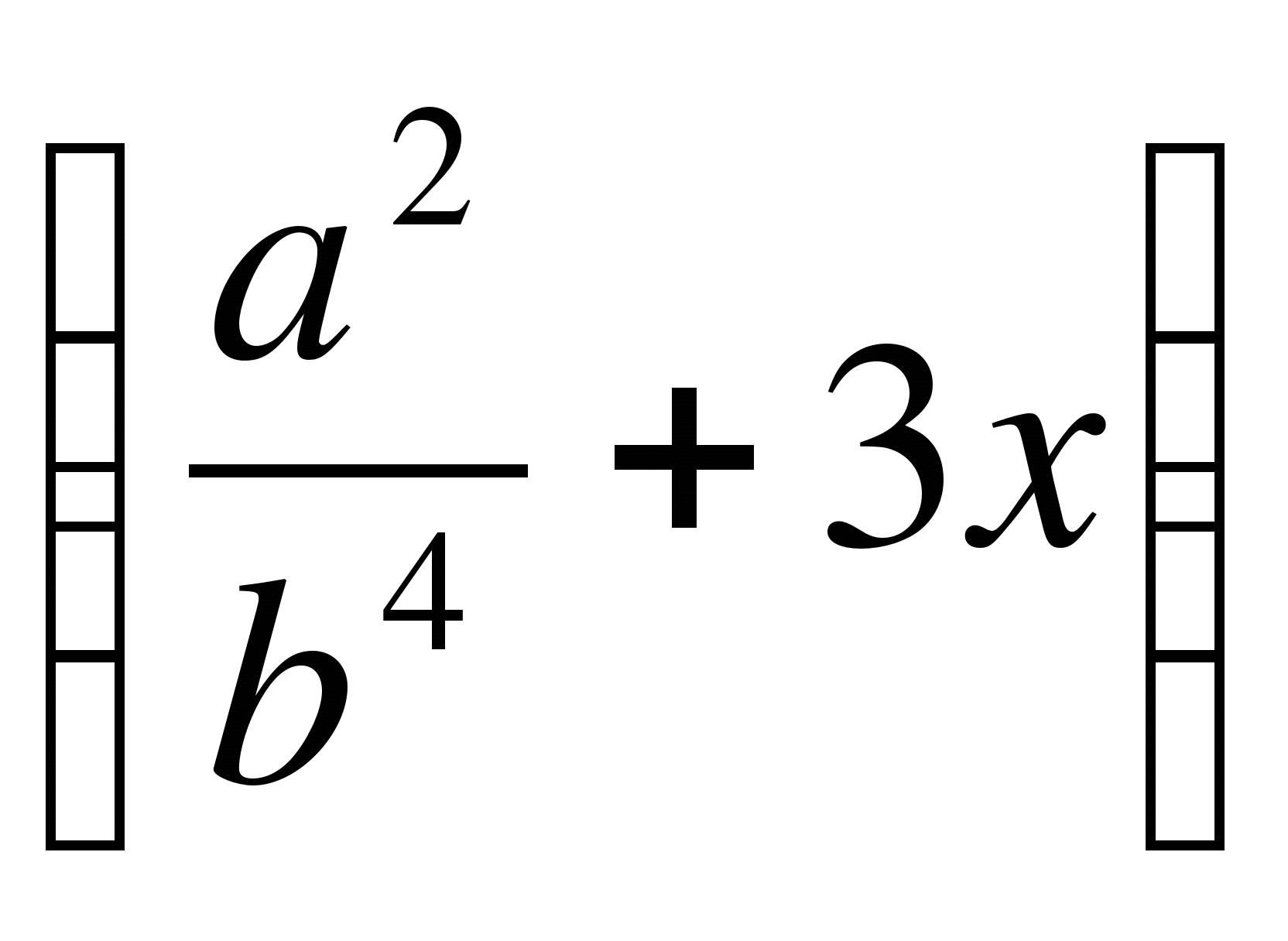 ;
;
2) (0,6 а2b + 0,8cу2)(0,6 а2b - 0,8 cу2);
3) (хn - 2)(хn + 2);
4) 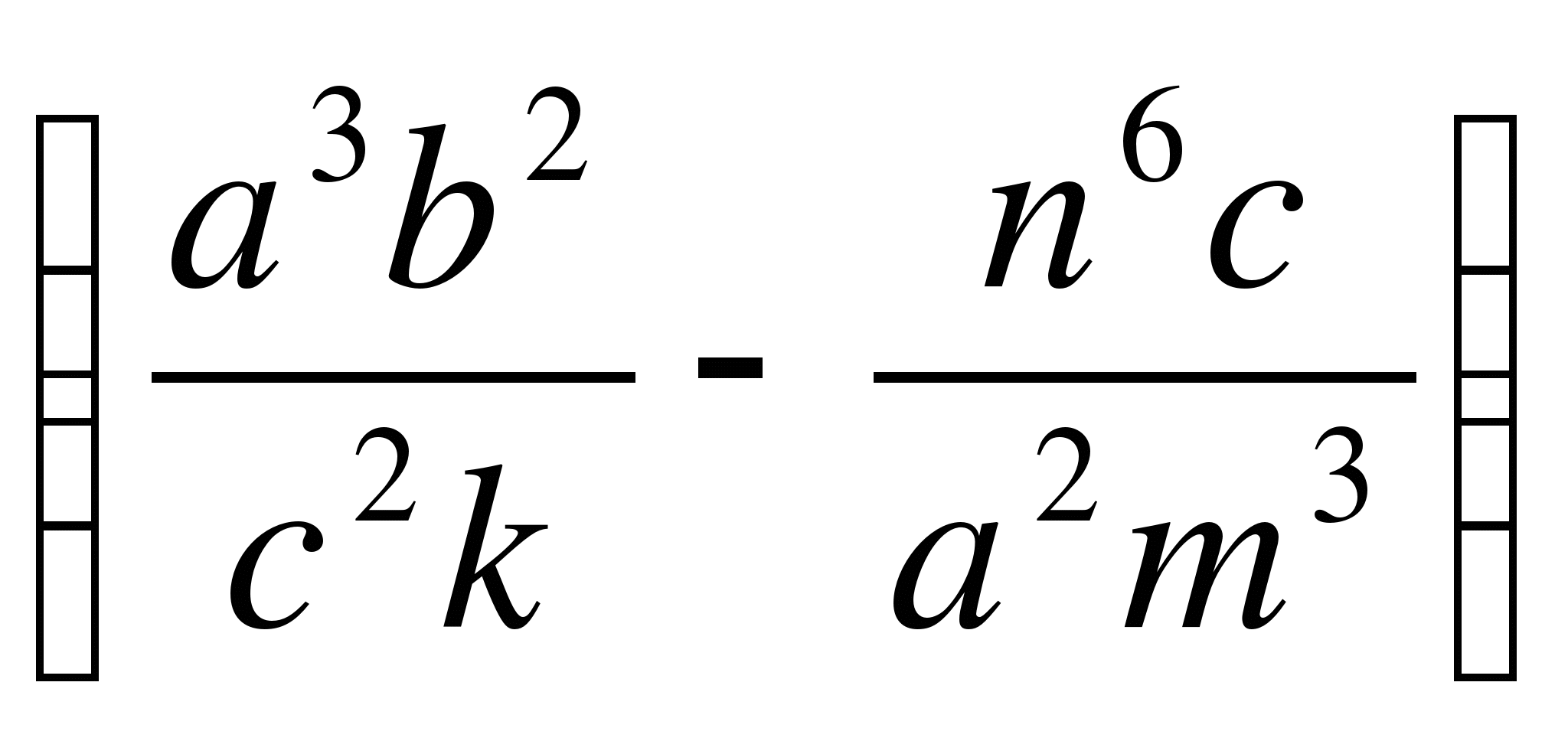
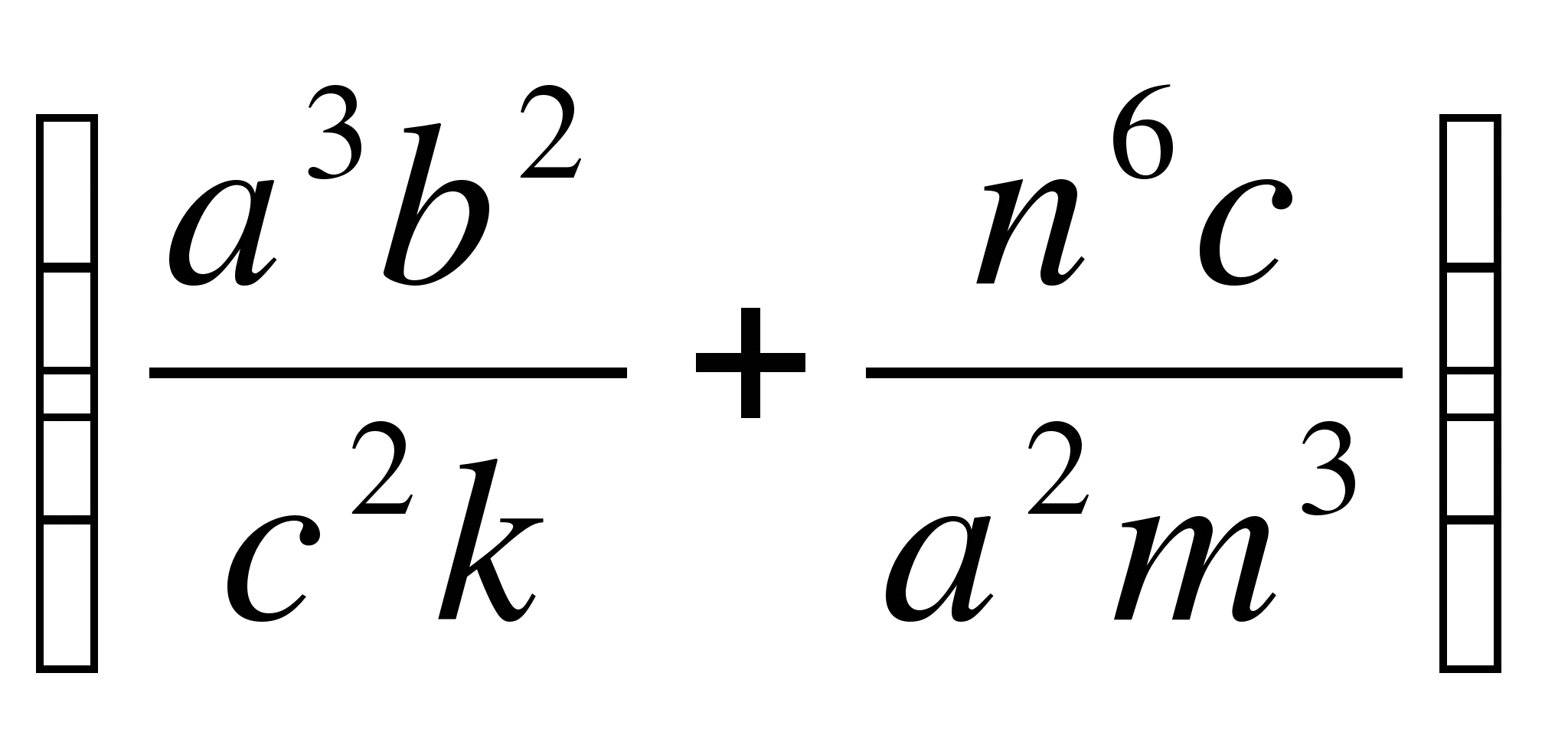 .
.
Вариант 3.
1. Разложите на множители
1)0,09х4у2 - 0,36z2; 2) 36х18 - 25у4;
3) ![]() ;
4) (2а + b)2 - 4a2.
;
4) (2а + b)2 - 4a2.
2. Выполни умножение:
1) 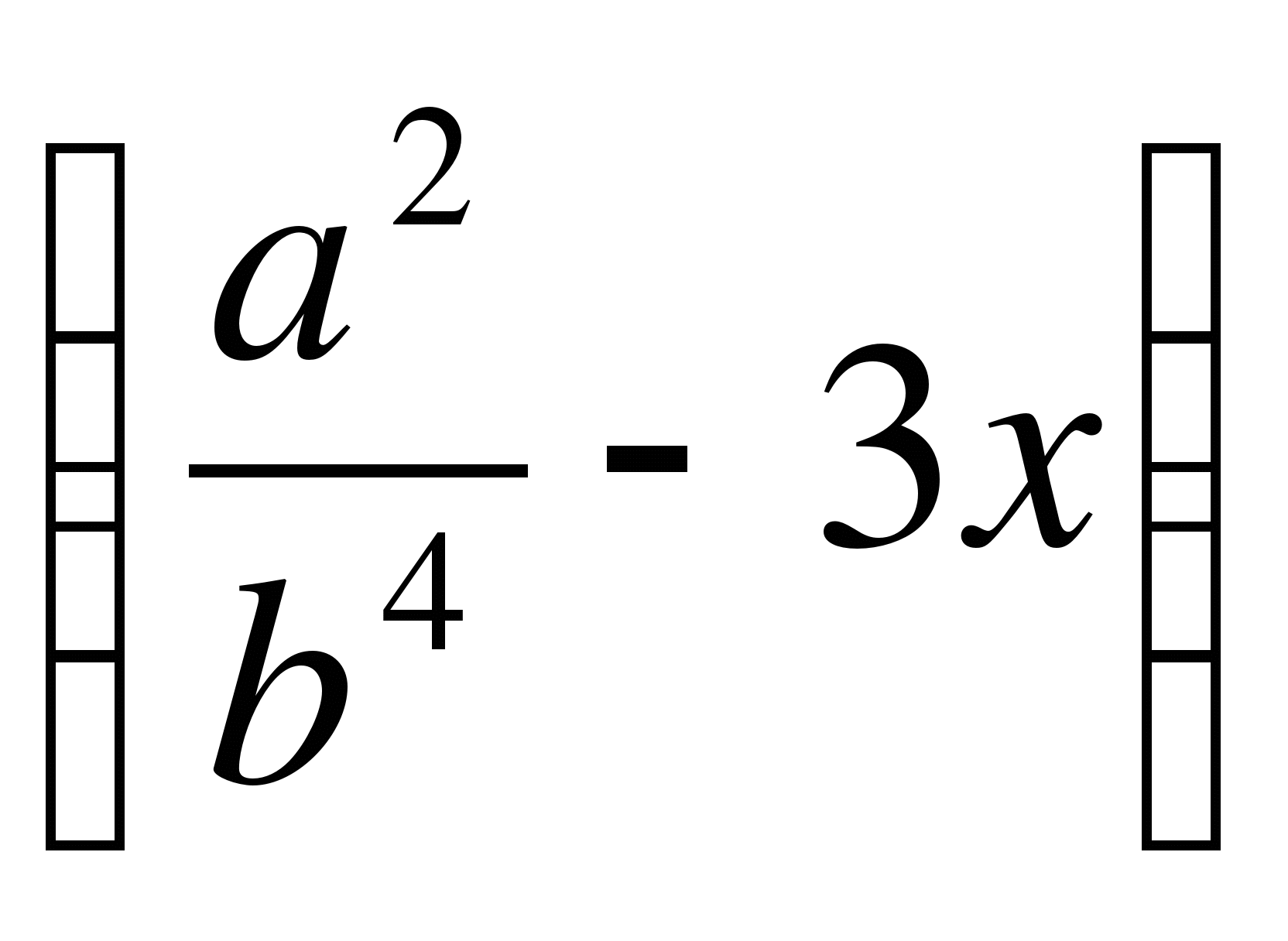
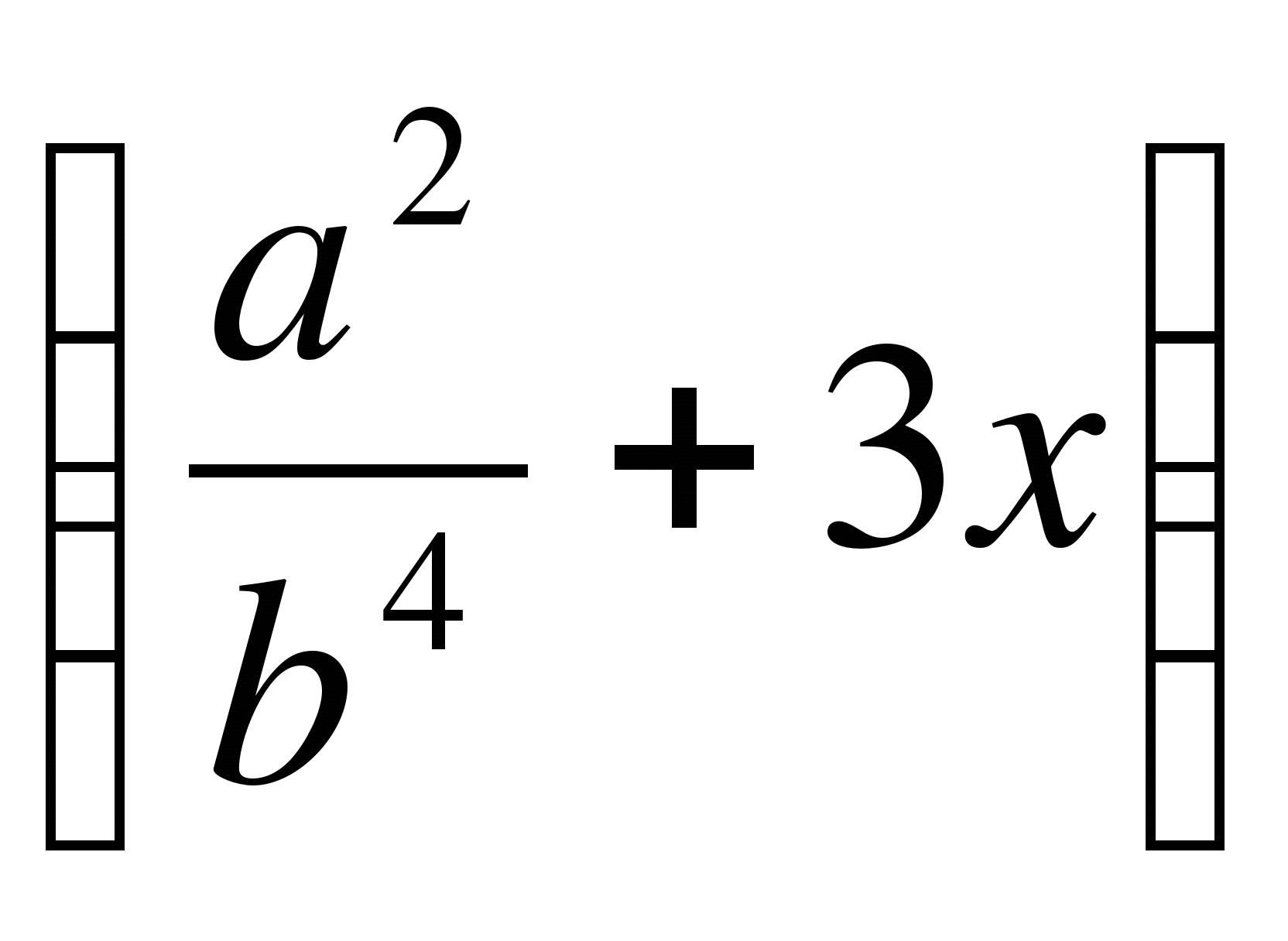 ;
;
2) (0,6 а2b + 0,8cу2)(0,6 а2b - 0,8 cу2);
3) (хn - 2)(хn + 2);
4) 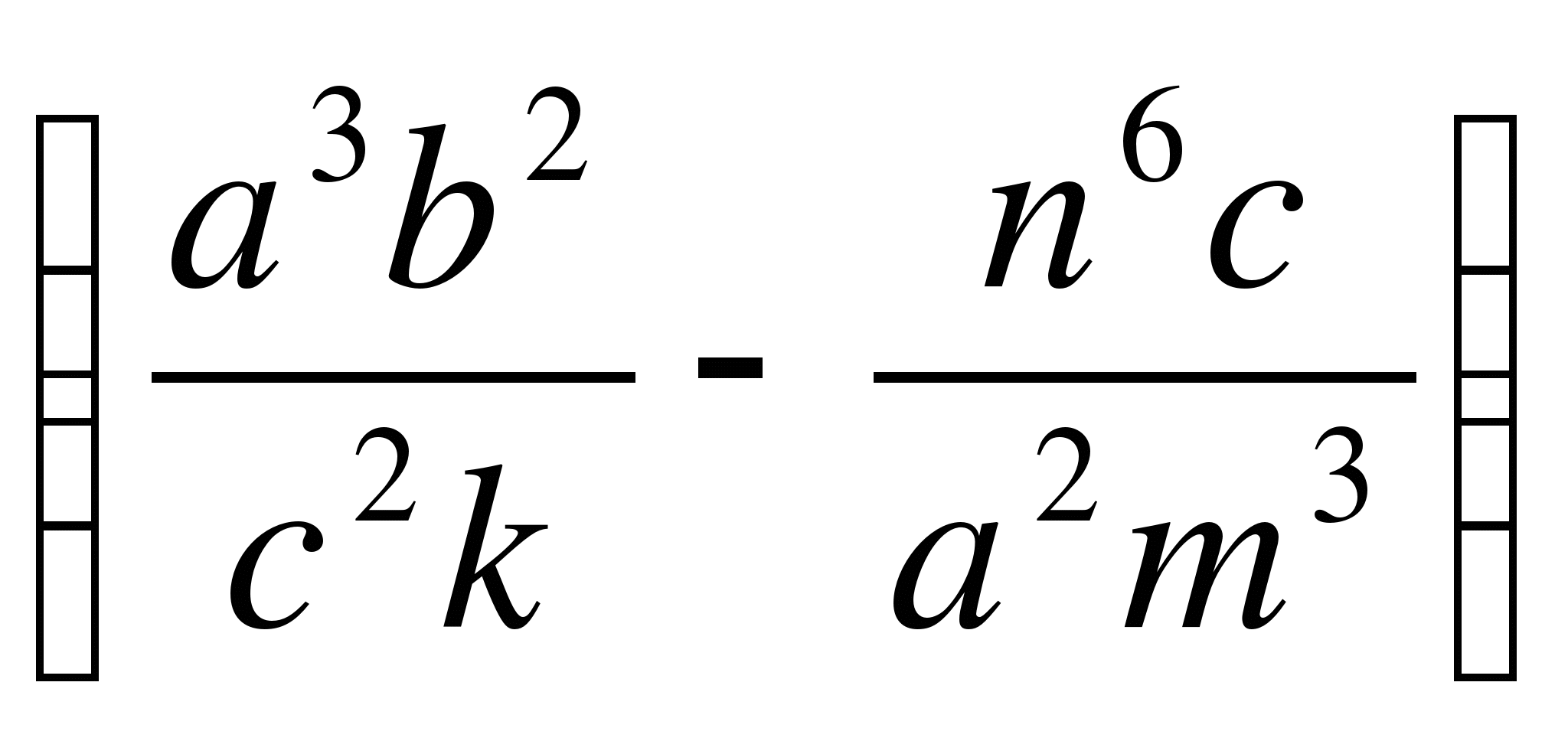
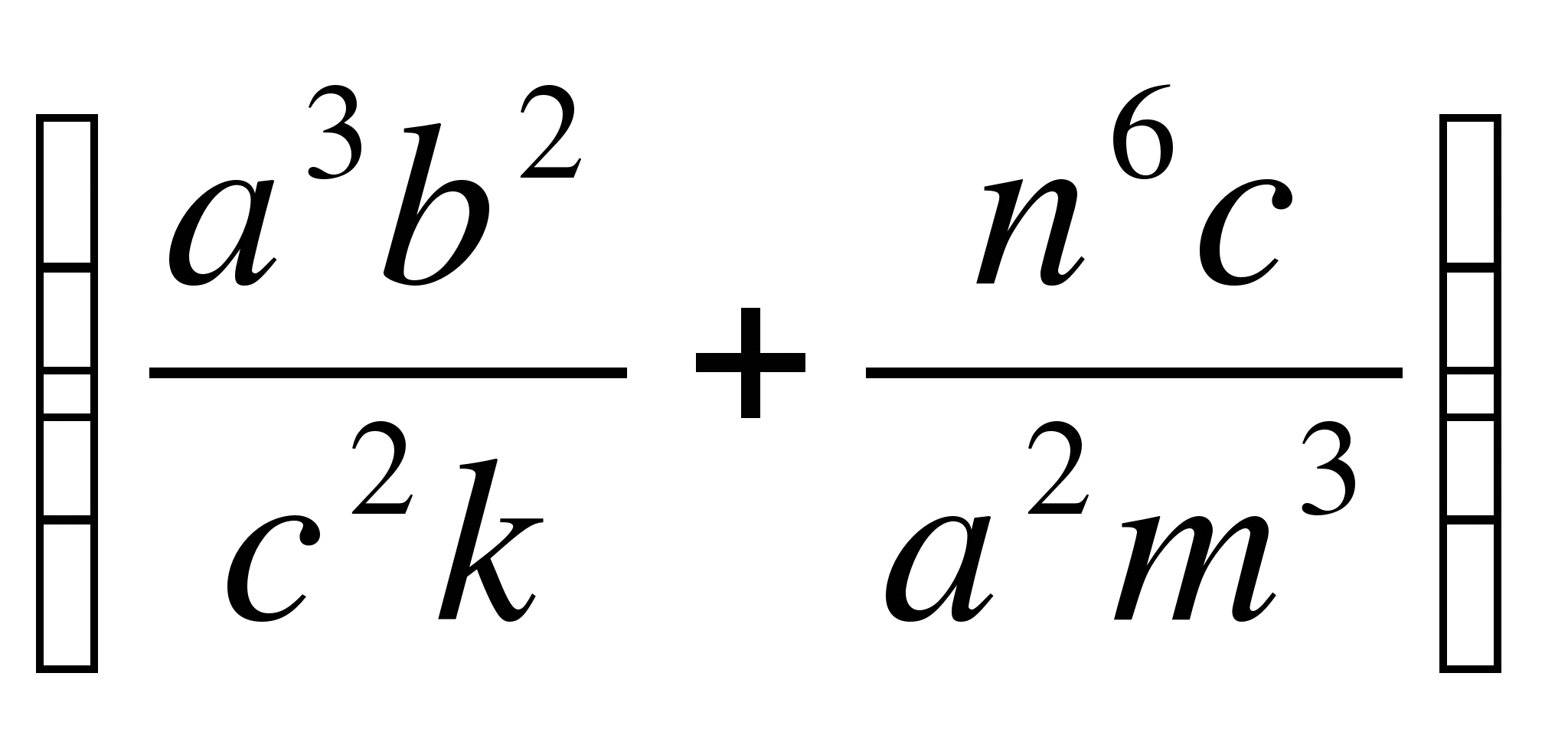 .
.
Самостоятельная работа по теме «Квадрат суммы. Квадрат разности.»
1. Возведите в квадрат:
1) (2а + 3b)2; 2) (7a - 3b)2; 3) (а2 + 1)2.
2. Разложите на множители:
1) х2 - 4ху + 4у2; 2) 9а2 + 24аb + 16b2.
Вариант 1.
1. Возведите в квадрат:
1) (2а + 3b)2; 2) (7a - 3b)2; 3) (а2 + 1)2.
2. Разложите на множители:
1) х2 - 4ху + 4у2; 2) 9а2 + 24аb + 16b2.
Вариант 2.
1. Возведите в квадрат:
1) (4a2 - 3b)2; 2) (5х
- 0,2у)2; 3) ![]()
2. Разложите на множители:
1) 36а8 + 84а4с3 + 49с6; 2) m2 + 25n2 - 10mn.
Вариант 2.
1. Возведите в квадрат:
1) (4a2 - 3b)2; 2) (5х
- 0,2у)2; 3) ![]()
2. Разложите на множители:
1) 36а8 + 84а4с3 + 49с6; 2) m2 + 25n2 - 10mn.
Вариант 3.
1. Возведите в квадрат:
1) ![]() ;
2)
;
2) ![]() ;
;
3) ![]() .
.
2. Разложите на множители:
1) - 121а2 + 66ab3 - 9b6; 2) 0,5k2 - km + 0,5m2.
Вариант 3.
1. Возведите в квадрат:
1) ![]() ;
2)
;
2) ![]() ;
;
3) ![]() .
.
2. Разложите на множители:
1) - 121а2 + 66ab3 - 9b6; 2) 0,5k2 - km + 0,5m2.
Разложите на множители
1) 3 x2 - 12
2) bx2 - 9b
3) 3a2 - 6ab + 3b2
4) -5a2 - 10ab - 5b2
5) x2(x - 3) - 2x(x - 3) + (x - 3)
6) ax + bx + ac + bc
7) 2a + 3a2 - b - ab
Вариант 2.
Разложите на множители
1) 5 x2 - 20
2) bx2 - 16b
3) 5a2 - 10ab + 5b2
4) -4a2 - 8ab - 4b2
5) (x + 7)c2 - (x + 7)2c + (x + 7)
6) ax - ay + bx - by
7) 3c + 3c2 - a - ac
Контрольная работа по теме «Разложение многочлена на множители»
Вариант 1.
1. Запишите выражение
25 - 12х + (х - 5)(х + 5) - (5 - х)2
в виде многочлена стандартного вида.
2. Разложите многочлен на множители:
а) 2ab - 3а; б) 6х6 +
8х2;
в) ![]() -
81; г) х2 - 12х + 36.
-
81; г) х2 - 12х + 36.
3. Представьте в виде произведения выражение
у(х + 0,2) - 2,7 (х + 0,2) найдите его числовое значение при х = 1,8; у = 16,7.
4. Разложите на множители:
а) 3х2 + 12xу + 12у2; б) 8a(b - 3) + с(3 - b);
в) х2 + 3х - 2ху - 6у.
5. Решите уравнение:
(х - 1)(х2 + х + 1)
- х2(х - 1) = 0.
Вариант 2.
1. Запишите выражение
(3 - х)2 - (х - 3)(х + 3) + 5х + 22
в виде многочлена стандартного вида.
2. Разложите многочлен на множители:
а) 3m - 3mn; б) 8x3 - 12х6;
в) 49 - ![]() ;
г) 64 + 16у + у2.
;
г) 64 + 16у + у2.
3. Представьте в виде произведения выражение
у(1,7 - х) - 4,3(1,7 - х) и найдите его числовое значение при х = 0,2, у = 12,3.
4. Разложите на множители:
а) 18а2 - 12аb + 2b2; б) 3а(b - 4) + 2с(4 - b); в) х2 + 2ху - 4х - 8y.
5. Решите уравнение:
х2(х + 2) - (х + 2)(х2 - х + 3) = 0.
Самостоятельная работа по теме «Алгебраические дроби приведение к новому знаменателю.»1 вариант
Приведите дроби к общему знаменателю
1) ![]() 2)
2)
![]()
3) ![]() 1)
1)
![]()
5) ![]()
2 вариант
Приведите дроби к общему знаменателю
1) ![]() 2)
2)
![]()
3) ![]() 1)
1)
![]()
5) ![]()
Самостоятельная работа по теме «Сложение и вычитание алгебраических дробей.»
1. Выполни сложение и вычитание дробей:
1) ![]() ;
2)
;
2) ![]() ;
;
3) ![]() ;
4)
;
4) ![]()
5) ![]() ;
6)
;
6) ![]() ;
;
7) ![]() ;
;
8) ![]()
9) ![]()
Вариант 2.
1. Выполни сложение и вычитание дробей:
1) ![]() ;
2)
;
2) ![]() ;
;
3) ![]() ;
4)
;
4) ![]()
5) ![]() ;
6)
;
6) ![]() ;
;
7) ![]() ;
;
8) ![]()
9)![]()
Самостоятельная работа по теме «Умножение и деление алгебраических дробей.»
1. Выполните умножение:
1) ![]() ;
2)
;
2) ![]() ;
;
3) ![]() ;
4)
;
4) ![]() ;
;
5) ![]() .
.
2. Выполните деление:
1) ![]() :
:
![]() ;
2)
;
2) ![]() :
:
![]() ;
;
3) ![]() :
:![]() ;
4)
;
4) ![]() :
:![]() ;
;
5) ![]() :
:
![]() .
.
Вариант 2.
1. Выполните умножение:
1) ![]() ;
2)
;
2) ![]() ;
;
3) ![]() ;
4)
;
4) ![]() ;
;
5) ![]() .
.
2. Выполните деление:
1) ![]() :
:
![]() ;
2)
;
2) ![]() :
:
![]() ;
;
3) ![]() :
:![]() ;
4)
;
4) ![]() :
:![]() ;
;
5) ![]() :
:
![]() .
.
Контрольная работа по теме «Алгебраические дроби»
Вариант 1.
1. Сократите дробь:
![]() .
.
2. Выполните действия:
а) ![]() ;
б)
;
б) ![]() ;
в)
;
в)![]() :
:
![]() .
.
3. Упростите выражение:
![]() .
.
4. Найти значение выражения:
![]() :
:
![]() ,
если x = 3
,
если x = 3
5. Решите уравнение:
![]()
Вариант 2.
1. Сократите дробь:
![]() .
.
2. Выполните действия:
а) ![]() ;
б)
;
б) ![]() ;
;
в) ![]() :
:
![]() .
.
3. Упростите выражение: ![]() .
.
4. Найти значение выражения:
![]() :
:
![]() ,
если b = 4
,
если b = 4
5. Решите уравнение:
![]()
Самостоятельная работа по теме «Функция»
1. Функция, задана формулой у = 4х - 8. Найдите у(- 3); у(0); у(1); у(6).
2. Найдите значение аргумента, при котором
функция у = - 2,5х принимает значение, равное 12; 7,5; - 4.
3. Заполните таблицу:
0
у = 0,8 - 0,4х
0,4
0
Вариант 2.
1. Функция, задана формулой у = 3х - 2. Найдите у(- 4); у(0); у(-1); у(10).
2. Найдите значение аргумента, при котором
функция у = - 1,4х принимает значение, равное 28; - 4,2; 7.
3. Заполните таблицу:
0
у = -0,6 - 0,3х
0,9
0
Самостоятельная работа по теме «Функция y = kx»
Вариант 1.
1. Для каждого графика функции заполните таблицу:
1) у = - 3х; 2) у = ![]() .
.
2
у
2. Постройте графики функций;
а) у = 5х; б) у = 1,2х; в) у = -
4х; г) у = -![]() .
.
3. Используя график функции у = 1,2х определите:
а) чему равно значение функции, если значение аргумента равно 4; 1; - 2,5; - 1.
б) при каком значении аргумента значение
функции равно 0; 1; - 3; - 5.
4. Функции заданы формулами у = - 2х, у
=![]() ,
,
у = ![]() , у
= 2х - 7. Укажите те из них, графиком которых является
прямая проходящая через начало координат, и постройте эти графики.
, у
= 2х - 7. Укажите те из них, графиком которых является
прямая проходящая через начало координат, и постройте эти графики.
Вариант 2.
1. Для каждого графика функции заполните таблицу:
1) у = 2,5х; 2) у = - 2х.
2
у
2. Постройте графики функций;
а) у = 4х; б) у = 1,5х; в) у = -
3х; г) у = -![]() х.
х.
3. Используя график функции у = 1,5х определите:
а) чему равно значение функции, если значение аргумента равно 1; 2; - 1,5; - 1.
б) при каком значении аргумента значение
функции равно 0; 2; - 2; - 3.
4. Функции заданы формулами у = 3х, у
=![]() ,
,
у = -![]() , у
= 3х + 2. Укажите те из них, графиком которых является
прямая проходящая через начало координат, и постройте эти графики.
, у
= 3х + 2. Укажите те из них, графиком которых является
прямая проходящая через начало координат, и постройте эти графики.
Контрольная работа по теме «Линейная функция и ее график»
Вариант 1.
1. Функция задана формулой y = 5x - 7. Определите:
а) значение функции при заданном значении аргумента 2; -1.
б) значение аргумента при заданном значении функции равном 8.
в) проходит ли график функции через точку
А(-7; -25)
2. В одной системе координат постройте графики функций: y = 3x; y = -2x + 2; y = - 4.
3. Дана функция y = 4x - 4. Найдите координаты точек пересечения графика функций с осями координат.
4. Найдите координаты точек пересечения графиков функций
y = -14x + 32 и y = 26x - 8
5. График функций y = kx + b пресекает ось ординат в точке А(0; -3) и проходит через точку В(4; 13). Найдите значения k и b, запишите получившуюся функцию.
Вариант 2.
1. Функция задана формулой y = 10x - 3. Определите:
а) значение функции при заданном значении аргумента -2; 3.
б) значение аргумента при заданном значении функции равном 7.
в) проходит ли график функции через точку
А(-3; -22)
2. В одной системе координат постройте графики функций: y = -2x; y = 3x + 1; y = 3.
3. Дана функция y = 5x - 10. Найдите координаты точек пересечения графика функций с осями координат.
4. Найдите координаты точек пересечения графиков функций
y = -10x - 9 и y = -24x + 19
5. График функций y = kx + b пресекает ось ординат в точке А(0; 4) и проходит через точку В(1; - 2). Найдите значения k и b, запишите получившуюся функцию.
Контрольная работа по теме «Система двух уравнений с двумя неизвестными»
Вариант 1.
1. Решите систему уравнений:
![]()
2. Решите задачу:
На ремонт 3 однокомнатных и 5 двухкомнатных квартир ушло 290 кусков обоев, а на ремонт 1 однокомнатной и 7 двухкомнатных квартир ушло 310 кусков обоев. Сколько кусков обоев требуется на ремонт однокомнатной и двухкомнатной квартиры?
3. Решите систему уравнений:
![]()
4. Прямая y = kx + b проходит через точку
А(2; 1) и точку В(- 4; 10). Найдите k и b, запишите уравнение этой прямой.
5. Выяснить, имеет ли решение система:
![]()
Вариант 2.
1. Решите систему уравнений:
![]()
2. Решите задачу:
Отряд туристов вышел на 9 байдарках, часть из которых двухместные, а часть - трехместные. Сколько двухместных, и сколько трехместных байдарок было в походе, если отряд туристов состоит из 23 человек?
3. Решите систему уравнений:
![]()
4. Прямая y = kx + b проходит через точку
А(6; 7) и точку В(- 2; 11). Найдите k и b, запишите уравнение этой прямой.
5. Выяснить, имеет ли решение система:
![]()
Итоговая контрольная работа
1. Упростите выражение:
а) (х - 2)2 - (х - 1)(х + 2);
б) ![]() .
.
2. Решите систему уравнений:
а)![]() ;
;
б) ![]() .
.
3. Постройте график функции
а) у = 2х + 2; проходит ли график функции через точку А(-10; - 18);
б) у = - 2х; укажите при каком значении аргумента значение функции равно -5.
4. Решите уравнение:
а) ![]() ;
б) 4(1 - 5х) = 9 - 3(6х - 5).
;
б) 4(1 - 5х) = 9 - 3(6х - 5).
5. Решите задачу:
Из пункта А в пункт В, расстояние между которыми 17 км вышел пешеход. Через 0,5 ч. навстречу ему из пункта В вышел второй пешеход и встретился с первым через 1,5 ч. после своего выхода. Найдите скорость каждого пешехода, если известно, что скорость первого на 2 км/ч меньше скорости второго.
Вариант 2.
1. Упростите выражение:
а) (у - 4)(у + 2) - (у - 2)2;
б) 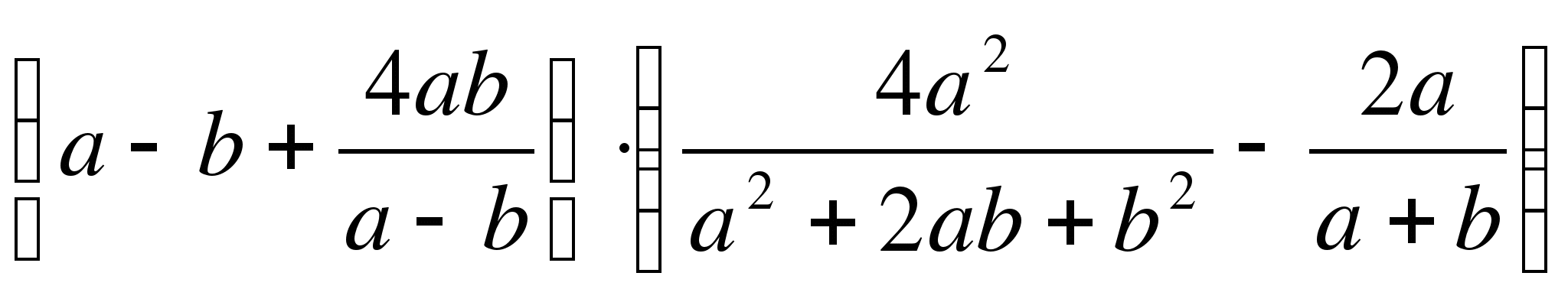 .
.
2. Решите систему уравнений:
а)![]() ;
;
б) ![]() .
.
3. Постройте график функции
а) у = -2х - 2; проходит ли график функции через точку А(10; - 22);
б) у = 2х; укажите при каком значении аргумента значение функции равно 5.
4. Решите уравнение:
а) ![]() ;
б) 3 - 4(1 - 6х) = 2(3х + 4).
;
б) 3 - 4(1 - 6х) = 2(3х + 4).
5. Решите задачу:
Из поселка на станцию, расстояние между которыми 32 км выехал велосипедист. Через 0,5 ч. навстречу ему со станции выехал мотоциклист и встретил велосипедиста через 0,5 ч. после своего выезда. Известно, что скорость мотоциклиста на
28 км/ч больше скорости велосипедиста. Найдите скорость каждого из них.
Самостоятельная работа
по теме «Свойства степени»
алгебра 7 класс
Самостоятельная работа по теме
«Решение уравнений»
алгебра 7 класс
Итоговая контрольная работа
7 класс
Самостоятельные работы по алгебре 7 класс
-
Самостоятельная работа по теме «Раскрытие скобок»
-
Самостоятельная работа по теме «Решение задач с помощью уравнений»
-
Самостоятельная работа по теме «Одночлены»
-
Самостоятельная работа по теме «Вынесение общего множителя за скобки »
-
Самостоятельная работа по теме «Разложение на множители способом группировки»
-
Самостоятельная работа по теме «Формула разности квадратов»
-
Самостоятельная работа по теме «Квадрат суммы. Квадрат разности.»
-
Самостоятельная работа по теме «Сложение и вычитание алгебраических дробей.»
-
Самостоятельная работа по теме «Умножение и деление алгебраических дробей.»
-
Самостоятельная работа по теме «Функция»
-
Самостоятельная работа по теме «Функция y = kx»
Самостоятельные работы по геометрии 7 класс
-
Самостоятельная работа по теме «Луч и угол»
-
Самостоятельная работа по теме «Первый признак равенства треугольников»
-
Самостоятельная работа по теме «Параллельные прямые»
-
Самостоятельная работа по теме «Луч и угол»
Контрольные работы по алгебре 7 класс
-
Контрольная работа по теме «Алгебраические выражения»
-
Контрольная работа по теме «Уравнения и его корни»
-
Контрольная работа по теме «Одночлены и многочлены»
-
Контрольная работа по теме «Разложение многочлена на множители»
-
Контрольная работа по теме «Алгебраические дроби»
-
Контрольная работа по теме «Линейная функция и ее график»
-
Контрольная работа по теме «Система двух уравнений с двумя неизвестными»
-
Итоговая контрольная работа
Контрольные работы по геометрии 7 класс
-
Контрольная работа по теме «Основные свойства простейших геометрических фигур»
-
Контрольная работа по теме «Треугольники»
-
Контрольная работа по теме «Параллельные прямые»
-
Контрольная работа по теме «Сумма углов треугольника. Неравенство треугольников»
-
Контрольная работа по теме «Соотношения между сторонами и углами треугольника»
Самостоятельная работа по теме
«Решение задач с
помощью уравнений»
алгебра 7 класс
Стоимость междугородного разговора вычисляется по формуле А = аn, где А - общая стоимость разговора, а - стоимость 1минуты, n-количество минут.
а) Подсчитайте стоимость междугородного разговора, если a = 8,5 руб.,n = 4 мин.
б) Сколько минут длиться разговор, если
А = 84 руб., а = 7руб.?
в) Запищите формулу, по которой можно вычислить продолжительность разговора n.
Вариант II
Стоимость покупки вычисляется по формуле
С = cm, где С - стоимость покупки, с - цена 1 кг товара, m - масса товара.
а) Вычислите стоимость купленного сахара, если с = 30 руб., m = 3 кг.
б) Сколько килограммов сахара купили, если
С = 70 руб., с =14 руб.?
в) Запишите формулу, по которой можно вычислить массу покупки m.
Вариант I
Стоимость междугородного разговора вычисляется по формуле А = аn, где А - общая стоимость разговора, а - стоимость 1минуты, n-количество минут.
а) Подсчитайте стоимость междугородного разговора, если a = 8,5 руб.,n = 4 мин.
б) Сколько минут длиться разговор, если
А = 84 руб., а = 7руб.?
в) Запищите формулу, по которой можно вычислить продолжительность разговора n.
Вариант II
Стоимость покупки вычисляется по формуле
С = cm, где С - стоимость покупки, с - цена 1 кг товара, m - масса товара.
а) Вычислите стоимость купленного сахара, если с = 30 руб., m = 3 кг.
б) Сколько килограммов сахара купили, если
С = 70 руб., с =14 руб.?
в) Запишите формулу, по которой можно вычислить массу покупки m.
Вариант I
Стоимость междугородного разговора вычисляется по формуле А = аn, где А - общая стоимость разговора, а - стоимость 1минуты, n-количество минут.
а) Подсчитайте стоимость междугородного разговора, если a = 8,5 руб.,n = 4 мин.
б) Сколько минут длиться разговор, если
А = 84 руб., а = 7руб.?
в) Запищите формулу, по которой можно вычислить продолжительность разговора n.
Вариант II
Стоимость покупки вычисляется по формуле
С = cm, где С - стоимость покупки, с - цена 1 кг товара, m - масса товара.
а) Вычислите стоимость купленного сахара, если с = 30 руб., m = 3 кг.
б) Сколько килограммов сахара купили, если
С = 70 руб., с =14 руб.?
в) Запишите формулу, по которой можно вычислить массу покупки m.
Вариант I
Стоимость междугородного разговора вычисляется по формуле А = аn, где А - общая стоимость разговора, а - стоимость 1минуты, n-количество минут.
а) Подсчитайте стоимость междугородного разговора, если a = 8,5 руб.,n = 4 мин.
б) Сколько минут длиться разговор, если
А = 84 руб., а = 7руб.?
в) Запищите формулу, по которой можно вычислить продолжительность разговора n.
Вариант II
Стоимость покупки вычисляется по формуле
С = cm, где С - стоимость покупки, с - цена 1 кг товара, m - масса товара.
а) Вычислите стоимость купленного сахара, если с = 30 руб., m = 3 кг.
б) Сколько килограммов сахара купили, если
С = 70 руб., с =14 руб.?
в) Запишите формулу, по которой можно вычислить массу покупки m.
Вариант I
Стоимость междугородного разговора вычисляется по формуле А = аn, где А - общая стоимость разговора, а - стоимость 1минуты, n-количество минут.
а) Подсчитайте стоимость междугородного разговора, если a = 8,5 руб.,n = 4 мин.
б) Сколько минут длиться разговор, если
А = 84 руб., а = 7руб.?
в) Запищите формулу, по которой можно вычислить продолжительность разговора n.
Вариант II
Стоимость покупки вычисляется по формуле
С = cm, где С - стоимость покупки, с - цена 1 кг товара, m - масса товара.
а) Вычислите стоимость купленного сахара, если с = 30 руб., m = 3 кг.
б) Сколько килограммов сахара купили, если
С = 70 руб., с =14 руб.?
в) Запишите формулу, по которой можно вычислить массу покупки m.