- Учителю
- Панорамный урок по алгебре в 8 классе на тему «Решение алгебраических уравнений степени выше второй»
Панорамный урок по алгебре в 8 классе на тему «Решение алгебраических уравнений степени выше второй»
Панорамный урок по алгебре в 8 классе
Учитель: Истляуп А.А., учитель математики школы-гимназии №17 г.Актобе
Тема урока: Решение алгебраических уравнений степени выше второй. Схема Горнера. Теорема Безу.
Цель урока:
Образовательная: ознакомить учащихся с приемами и методами решения уравнений высших степеней, схемой Горнера, теоремой Безу.
Развивающая: уметь решать уравнения высших степеней, уметь делить многочлен на двучлен, используя схему Горнера, теорему Безу.
Воспитательная: воспитать у учащихся интерес к предмету.
Ход урока:
-
Организационный момент.
-
Актуализация знаний.
-
Введение знаний.
-
Воспроизведение знаний.
-
Итог урока.
Одним из способов решения уравнений высших степеней является способ разложения на множители многочлена, стоящего в левой части уравнения. Этот способ основан на следующем применении теоремы Безу.
![]() - многочлен n-ой степени
- многочлен n-ой степени ![]() - старший коэффициент,
- старший коэффициент, ![]() - свободный член.
- свободный член.
Если ![]() , то получим уравнение n-ой степени, короче
, то получим уравнение n-ой степени, короче ![]() .
.
Если известен хотя бы один корень ![]() алгебраического уравнения, то нахождение остальных корней этого уравнения сводится к решению уравнения, имеющего на единицу меньшую степень, чем исходное уравнение.
алгебраического уравнения, то нахождение остальных корней этого уравнения сводится к решению уравнения, имеющего на единицу меньшую степень, чем исходное уравнение.
При решении алгебраических уравнений ![]()
![]() можно использовать метод понижения степени уравнения, основанный на теореме Безу и делении многочлена
можно использовать метод понижения степени уравнения, основанный на теореме Безу и делении многочлена ![]() на одночлен
на одночлен ![]() , где
, где ![]() - корень уравнения
- корень уравнения ![]() .
.
Определение. Значение ![]() , при котором многочлен
, при котором многочлен ![]() обращается в нуль называется корнем этого многочлена.
обращается в нуль называется корнем этого многочлена.
Если алгебраическое уравнение с целыми коэффициентами имеет целее корни, то каждый из этих корней является делителем свободного члена.
Решить уравнение ![]()
1 способ: ![]()
Группируем 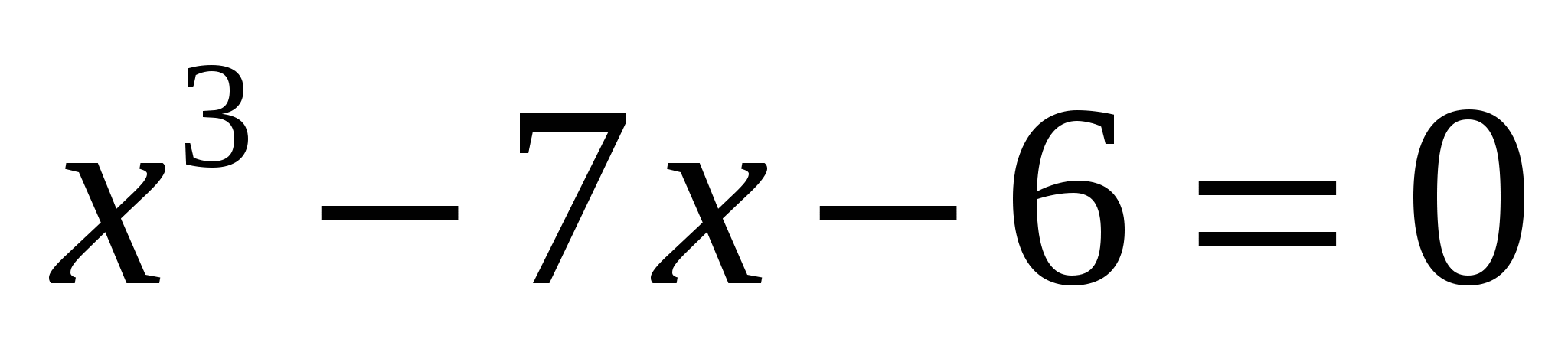
![]() или
или ![]()
2 способ: выпишем делители свободного члена ![]()
А) найдем хотя бы один корень данного уравнения, нетрудно догадаться, что корнем этого уравнения является ![]() .
.
По следствию теорем Безу, если ![]() - корень многочлена
- корень многочлена ![]() , то этот многочлен делится на двучлен
, то этот многочлен делится на двучлен ![]() , т.е. на
, т.е. на ![]() , т.е. снизили степень данного уравнения на единицу.
, т.е. снизили степень данного уравнения на единицу.
Б) Для этого по схеме Горнера разделили этот многочлен на двучлен ![]() .
.
-
1
0
-7
-6
-1
1
-1
-6
0
тогда получим уравнение ![]() , корни которого
, корни которого ![]() ,
, ![]() ,
, ![]() .
.
Ответ: -2; -1; 3
Решить уравнение ![]()
А) находим делитель свободного члена: ![]() .
.
Б) найдем хотя бы один корень данного уравнения. Очевидно, что при ![]() значение многочлена равно 0.
значение многочлена равно 0. ![]() . Следовательно,
. Следовательно, ![]() является корнем уравнения третьей степени.
является корнем уравнения третьей степени.
В) применяя теорему Безу, снизим степень уравнения на единицу, деля данный многочлен на двучлен ![]() , где
, где ![]() , т.е. имеем
, т.е. имеем ![]() .
.
Г) деление произведем по схеме Горнера:
-
1
-2
-5
6
1
1
-1
-6
0
Получим уравнение: ![]()
Д) приравнивая каждый многочлен к нулю: (произведение равно нулю, если один из множителей равен 0)
![]() или
или ![]()
Ответ: -2; 1; 3
Решить уравнение ![]()
А) находим делитель свободного члена: ![]() .
.
Б) найдем хотя бы один корень данного уравнения. Для этого находим значение многочлена ![]() в этих точках.
в этих точках.
![]() .
.
![]()
![]()
![]()
Следовательно, данное уравнение имеет один корень ![]() , а числа
, а числа ![]() не являются корнями.
не являются корнями.
В) если известен хотя бы один корень ![]() алгебраического уравнения, то нахождение остальных корней сводится к решению уравнения, имеющего на единицу меньшую степень, чем исходное уравнение, т.е.снизим степень уравнения на единицу, т.е.
алгебраического уравнения, то нахождение остальных корней сводится к решению уравнения, имеющего на единицу меньшую степень, чем исходное уравнение, т.е.снизим степень уравнения на единицу, т.е.![]() .
.
Г) найдем коэффициенты уравнения ![]() , произведя деление данного многочлена
, произведя деление данного многочлена ![]() на двучлен
на двучлен ![]() по схеме Горнера:
по схеме Горнера:
-
1
2
-2
-6
5
1
1
3
1
5
0
Получим уравнение: ![]()
Д) снизим степень уравнения ![]() на единицу.
на единицу.
1) найдем делители свободного члена ![]() ;
;
2) числа ![]() не являются корнями исходного уравнения;
не являются корнями исходного уравнения;
3) произведем деление многочлена ![]() на двучлен
на двучлен ![]() по схеме Горнера:
по схеме Горнера:
-
1
3
1
-5
1
1
4
5
0
4) получим уравнение ![]()
![]() или
или 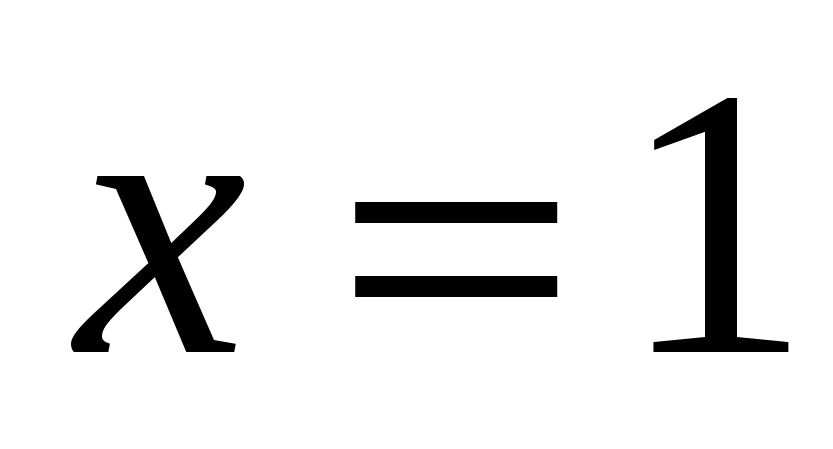 уравнение корней не имеет
уравнение корней не имеет
Ответ: 1
Итог: Вопросы:
1) При решении уравнений третьей степени какой способ решения уравнений вам проще применять?
Ответ: второй, а именно теорему Безу и схему Горнера
2) Как будете решать уравнение степени выше третьей?
Ответ: находим среди делителей свободного члена хотя бы один корень, а затем по теореме Безу будем понижать степень уравнения, раскладывая многочлен на множители до тех пор пока не получим уравнение, которое мы можем решать.