Урок по алгебре для 8 класса «ПОСТРОЕНИЕ ГРАФИКОВ ФУНКЦИЙ, СОДЕРЖАЩИХ АБСОЛЮТНЫЕ ВЕЛИЧИНЫ»

Открытый урок по алгебре 8 класс

Учитель МБОУ СОШ №8 ЛАСТОВЫРЯ Т.Г.

Комбинированный урок по теме:

«ПОСТРОЕНИЕ ГРАФИКОВ ФУНКЦИЙ, СОДЕРЖАЩИХ АБСОЛЮТНЫЕ ВЕЛИЧИНЫ »

Цели урока:

• образовательная: научить учащихся строить графики, содержащие модуль; закрепить изученный материал в ходе выполнения упражнений; провести диагностику усвоения знаний и умений применения их при выполнении практических заданий стандартного и более высокого уровня сложности.

• развивающая: развитие умений строить графики функций; развитие осмысленного отношения к своей деятельности; развитие самостоятельности мышления: видеть общую закономерность, делать обобщения и выводы.

• воспитательная: воспитание аккуратности.

Задачи урока:

• закрепление основ знаний о функциях и их графиках;

• формирование умений «читать» графики и преобразовывать их;

• вовлечение учащихся в игровую, коммуникативную, практическую деятельность как фактор личностного развития.

Форма организации урока: лекция, самостоятельная работа.

Оборудование: презентация, включающая примеры заданий и тестовый материал.

Продолжительность: 40 мин.

Структура урока:

1.Сообщение темы и цели урока (1 мин).

2.Повторение изученного материала (5 мин).

3. Изучение новой темы (10 мин).

4.Закрепление изученного материала (15 мин).

5.Подведение итогов урока (7 мин).

6.Постановка домашнего задания (2 мин).

7.Резервные задания.

Ход урока.

1.Сообщение темы и цели урока

После проверки подготовленности классного помещения и готовности, учащихся к уроку, отмечается, что сегодня проводится урок, посвященный построению графика функции, содержащей модуль, двумя способами: по определению и с помощью преобразования.

Ставится задача: научиться строить графики функций, содержащие модуль.

2.Повторение изученного материала

• Повторить определение модуля неотрицательного и отрицательного числа.

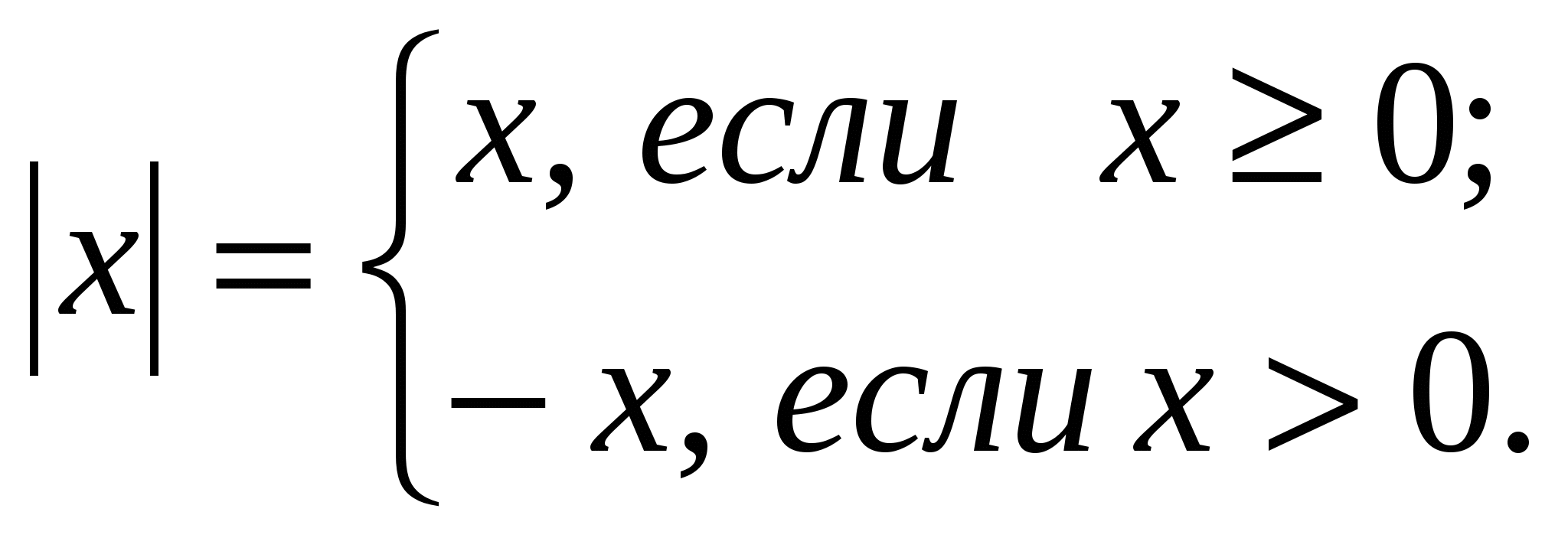
• Повторить построение графиков простейших функций (линейная, квадратичная, 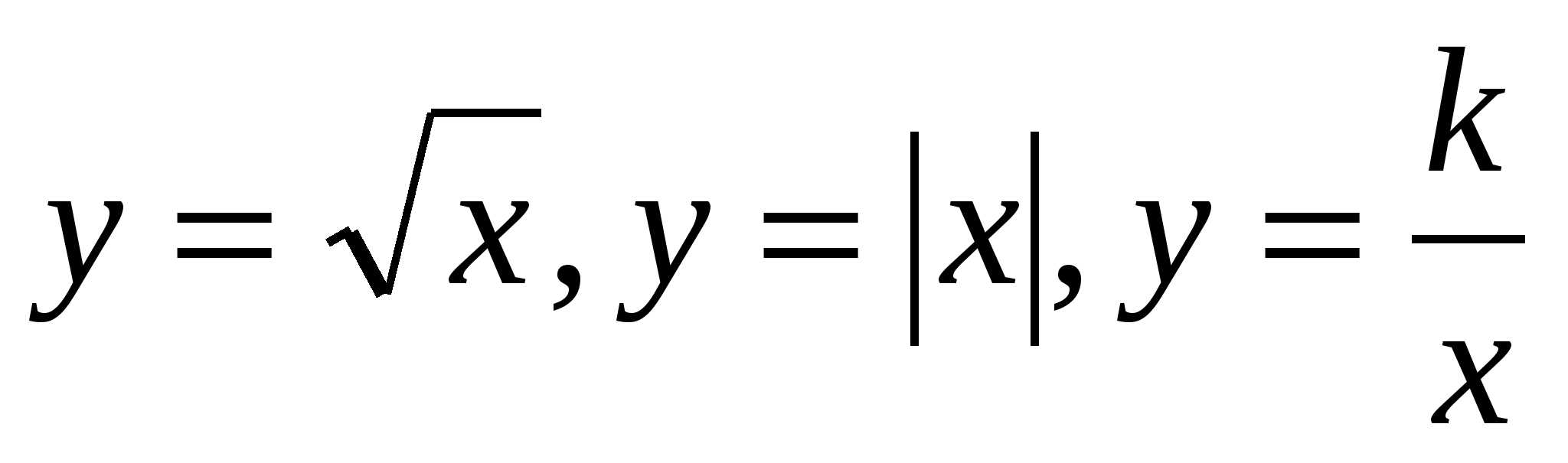). Изобразить их схематически.

3. Изучение новой темы по плану:

1) Построение графика функции

2) Построение графика функции

3) Построение графика функции

Целесообразно рассматривать построение графиков в следующей последовательности:

Построение графиков следует осуществлять двумя способами:

1. на основании определения модуля;

2. на основании правил (алгоритмов) геометрического преобразования графиков функций.

Построение графика функции

Следовательно, график функции состоит из двух графиков: - в правой полуплоскости, - в левой полуплоскости.

Исходя из этого, можно сформулировать правило (алгоритм).

График функции получается из графика функции следующим образом: при x0 график сохраняется, а при x<0 часть графика в правой полуплоскости отображается симметрично относительно оси Oy.

Построение графика функции

Отсюда вытекает алгоритм построения графиков функции .

а) Строим график функции f(x).

б) Часть графика, лежащая над осью Ox, сохраняется, часть его, лежащая под осью Ox, отображается симметрично относительно оси Ox.

Построение графика функции

Правило (алгоритм) построения.

Чтобы построить график функции , надо сначала построить график функции y=f(x) при x>0, затем при x<0 построить изображение, симметричное ему относительно оси Oy, а затем на интервалах, где , построить изображение, симметричное графику относительно оси Ox.

4.Закрепление изученного материала

Рассмотрим построение графиков функций на примерах.

Пример 1.

Построить график функции

Построение.

1-й способ.

Построим, опираясь на определение модуля действительного числа (слайд 3 - 7).

2-й способ.

Построим, используя способы преобразования графика функции (слайд 8 - 10).

а) Строим график функции для x>0.

б) Достраиваем его левую часть для x<0, симметрично построенной относительно оси Oy.

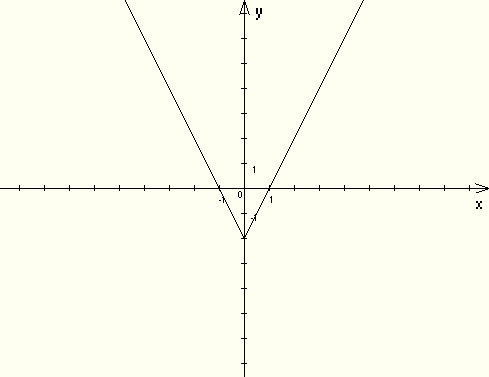
II

I

Пример 2.

Построить график функции

Построение.

1-й способ.

Строим график кусочной функции по определению модуля (слайд 11 - 15).

2-й способ.

Строим на основе преобразования графика уже известной нам функции.

а) Строим график функции y=x-2.

б) График нижней полуплоскости отображаем вверх симметрично относительно оси Ox.

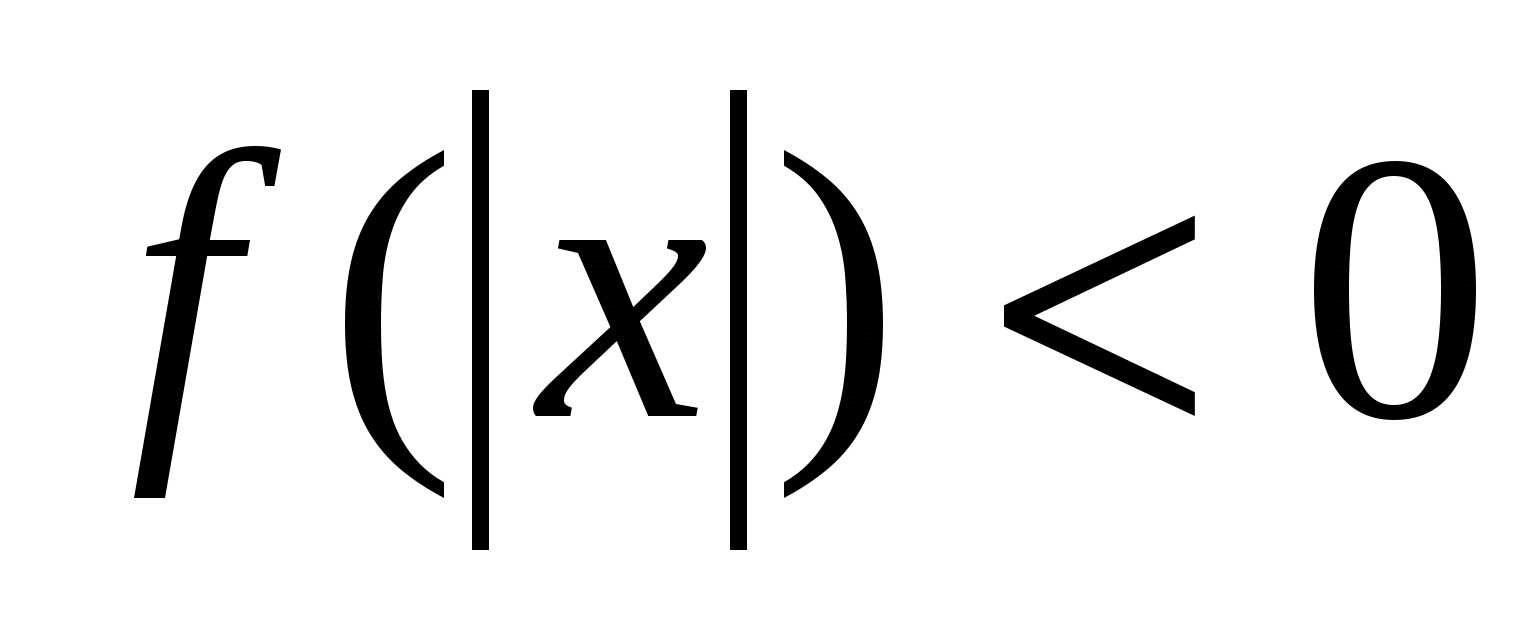
Пример 3.

Построить график функции .

Построение.

1-й способ.

Построим на основе определения модуля действительного числа (слайд 17 - 22).

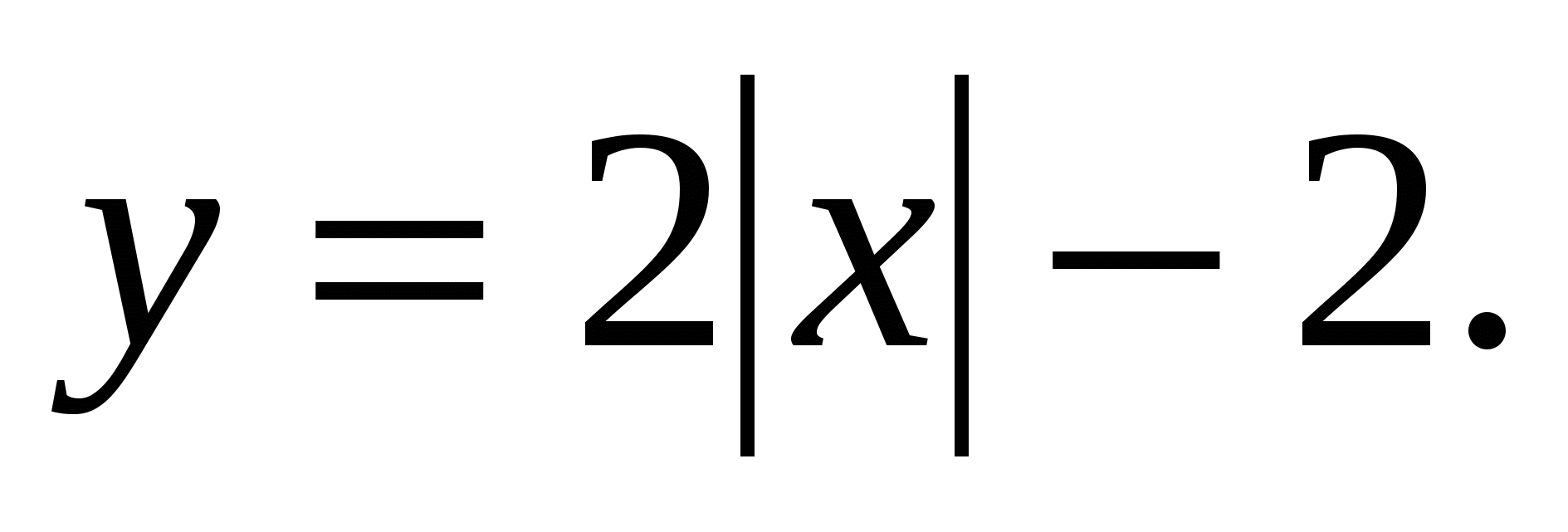
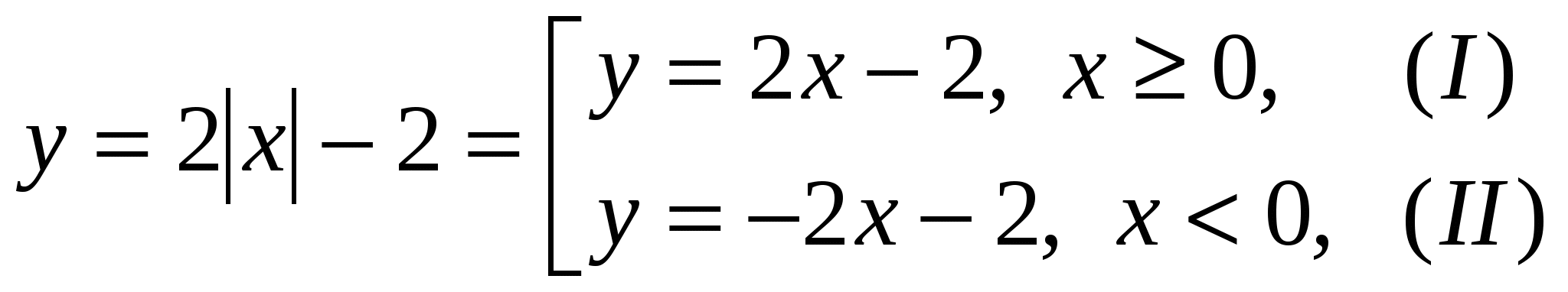
2-й способ.

Построим на основе простейших способов преобразования графика функции (слайд 23 - 26).

1) Строим график функции .

2) График функции , получаем из графика функции отражением симметрично (при ) относительно оси Oy.

3) График функции , получаем из графика функции отображением симметрично оси Ox нижней части графика.

5.Подведение итогов урока

Проведение тестовой самостоятельной работы, используя презентацию (слайд 28 - 30).

6.Постановка домашнего задания

Домашнее задание дается на карточках на основе дифференцированного подхода (Приложение).

7. Резервные задания

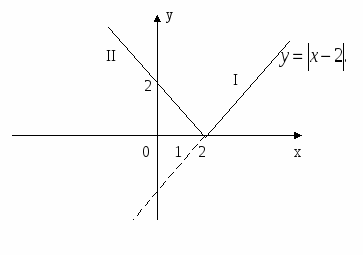
Приложение

Номер карточки соответствует уровню сложности.

П

Iостройте графики функций двумя способами: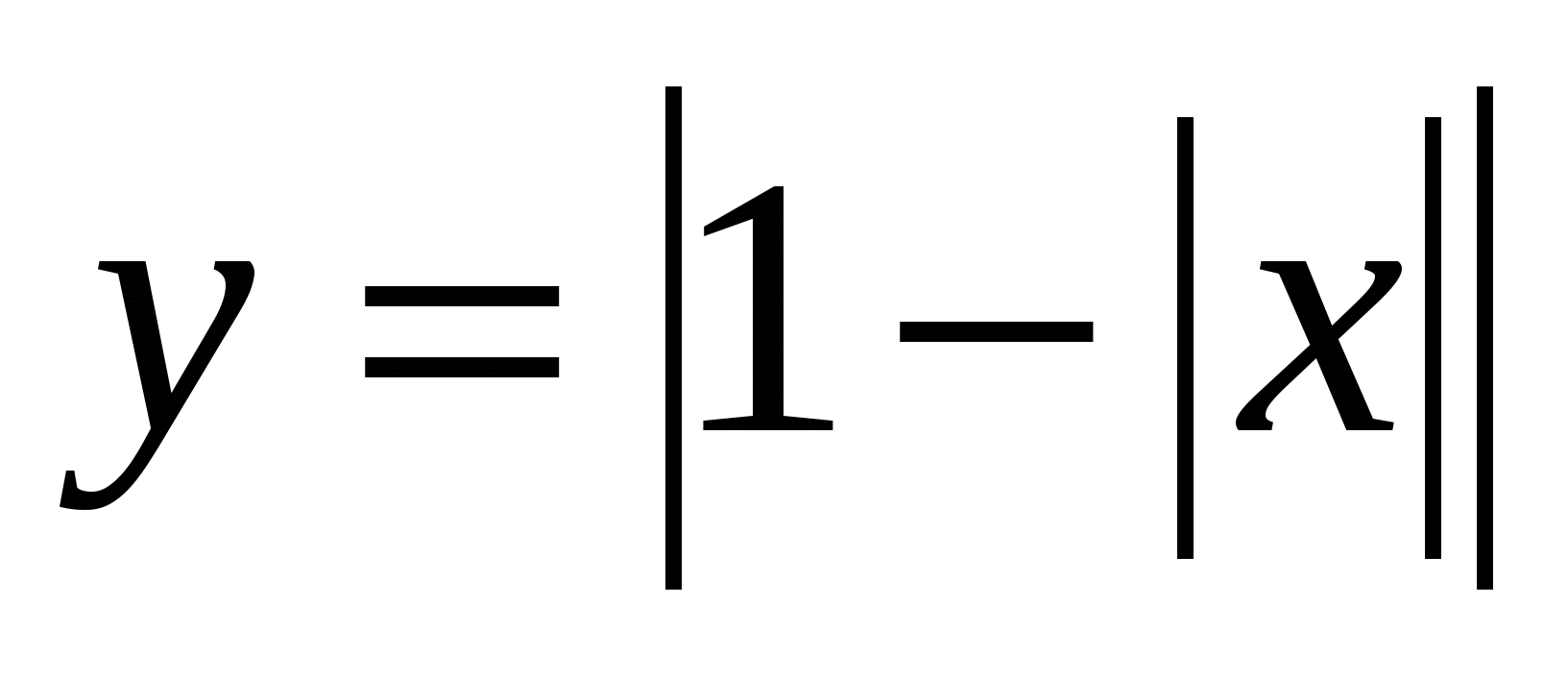

П

Iостройте графики функций двумя способами: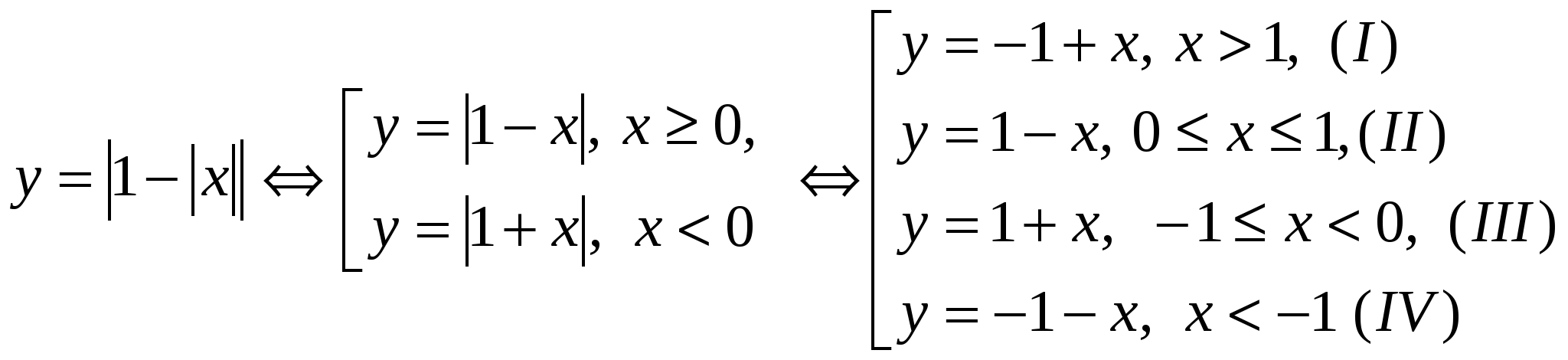

IIПостройте графики функций двумя способами: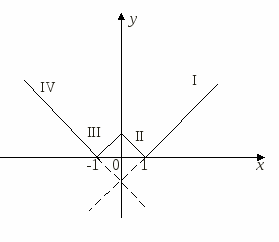

IIПостройте графики функций двумя способами: