Конспект урока по теме Треугольник и его элементы

Тема: Треугольник и его элементы.

ЦЕЛИ:

1. Изучить понятие треугольника и его элементов в ходе практической работы;

2. Развитие логического мышления учащихся. Формирование устойчивого познавательного интереса к изучению геометрии.

3. Воспитание отношений взаимопомощи и сотрудничества между учащимися в процессе познавательной деятельности; развитие их самостоятельности и творчества.

ХОД УРОКА

1. Организационный момент.

2. Мотивация урока.

Кто из вас не слышал о загадочном Бермудском треугольнике, в котором бесследно исчезают корабли и самолёты? (Он находится в Атлантическом океане между Бермудскими островами, государством Пуэрто-Рико и полуостровом Флорида).

А ведь знакомый всем нам треугольник также таит в себе немало интересного и загадочного.

Зовётся он треугольник,

И с ним хлопот не оберётся школьник!

3. Актуализация опорных знаний.

Среди множества различных геометрических фигур на плоскости выделяется большое семейство МНОГОУГОЛЬНИКОВ.

Названия геометрических фигур имеют вполне определенный смысл. Присмотритесь внимательно к слову "многоугольник", и скажите из каких частей оно состоит. Слово "многоугольник" указывает на то, что у всех фигур этого семейства "много углов".

Подставьте в слово "многоугольник" вместо части "много" конкретное число, например 5. Вы получите ПЯТИУГОЛЬНИК. Или 6. Тогда - ШЕСТИУГОЛЬНИК. Заметьте, сколько углов, столько и сторон, поэтому эти фигуры вполне можно было бы назвать и многосторонниками.

На рисунке геометрические фигуры. Используя рисунок, назовите эти фигуры.

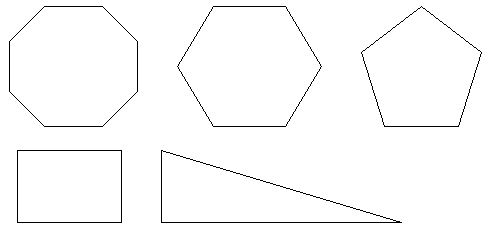
Каким наименьшим числом можно заменить "много" в многоугольнике? (Ответ: 3)

4. Изучение нового материала.

Часто знает и дошкольник,

Что такое треугольник,

А уж вам-то, как не знать…

Но совсем другое дело -

Очень быстро и умело

Треугольники считать!

Например, в фигуре этой

Сколько разных? Рассмотри!

Все внимательно исследуй

И "по краю" и "внутри".

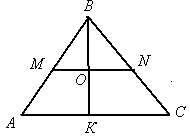
Треугольник - простейшая фигура: три стороны, три вершины, три угла. Математики называют его двумерным "симплексом" - по латыни означает простейший. Именно в силу своей простоты треугольник явился основой многих измерений.

Через площадь треугольника выражается площадь любого многоугольника, достаточно разбить этот многоугольник на треугольники, вычислить их площади и сложить результаты.

Еще 4000 лет назад в одном египетском папирусе говорилось о площади треугольника.

Через 2000 лет в Древней Греции очень активно велось изучение свойств треугольника. Пифагор открыл свою знаменитую формулу.

Особенно плодотворно свойства треугольника исследовались в XV-XVI веках. Большой вклад в эту теорию внес знаменитый математик Леонард Эйлер.

Император Франции Наполеон свободное время посвящал занятием математики и, в частности, изучению свойства треугольников.

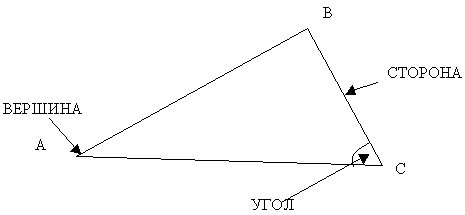
ТРЕУГОЛЬНИК - геометрическая фигура, состоящая из трех точек (вершин) и трех попарно соединяющих их отрезков (стороны).

Задача

Земельный участок имеет треугольную форму. Сколько потребуется метров проволоки, чтобы обнести этот участок забором?

(Ответ: измерить стороны и сложить их длины.)

Как мы называем сумму длин всех сторон треугольника?

(Ответ: периметр.)

Р = АВ + ВС + СА (ед.)

Практическая работа.

Медиана.

Начертите треугольник АВС и найдите середину стороны ВС - точку М.

Что называется серединой отрезка? (Серединой отрезка называется точка отрезка, которая делит его пополам, то есть на два равных отрезка).

Запись на доске: АМ=МС.

Соедините точку М с вершиной В. Отрезок ВМ называется медианой треугольника.

Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.

Сколько вершин у треугольника? (3).

Сколько у него сторон? (3).

Сколько медиан можно провести в треугольнике?(3).

"Проведите" три медианы на моделях треугольников.

Какое свойство медиан вы заметили?

В любом треугольнике все медианы пересекаются в одной точке.

Эта точка называется центром тяжести треугольника.

Высота.

Запись на доске: ВН АС.

С помощью чертёжного угольника из вершины В треугольника АВС проведём перпендикуляр ВН к прямой АС. Он называется высотой треугольника.

Высотой треугольника называется перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противолежащую сторону.

Сколько высот имеет треугольник? (3).

"Постройте" все три высоты на модели вашего треугольника. Обладают ли высоты аналогичным свойством, что и медианы? (Да). Высоты или их продолжения пересекаются в одной точке.

Биссектриса.

Вспомните определение биссектрисы угла.

Луч, исходящий из вершины угла и делящий его на два равных угла, называется биссектрисой угла.

Запись на доске: АВК = СВК

Постройте биссектрису ВК угла В с помощью транспортира. Она пересечёт отрезок АС в точке К. Отрезок ВК называется биссектрисой угла В треугольника АВС.

Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину угла треугольника с точкой противоположной стороны треугольника.

Покажите все три биссектрисы на вашей модели треугольника.

Сформулируйте свойство биссектрис треугольника.

В любом треугольнике биссектрисы пересекаются в одной точке.

Классификация треугольников.

По величине углов

1). Остроугольные.

2). Прямоугольные.

3). Тупоугольные.

По длине сторон:

• Разносторонние.

• Равнобедренные.

• Равносторонние.

"Перпендикуляр" - от латинского слова "PERPENDICULARIS" - "отвесный". Термин был образован в средние века.

"Биссектриса" - от латинских слов (дважды, надвое) и "SECTRIX" - "секущая".

"Медиана" - от латинского слова "MEDIANA" - "средняя" (линия).

5. Закрепление нового материала.

Решить № 260, 261, 269(а).

6. Итоги урока. Рефлексия.

Что больше всего тебе запомнилось на уроке?

Что удивило?

Что понравились больше всего?

Каким ты хочешь увидеть следующий урок?

Домашнее задание: выучить п.9, вопросы с.77, решить № 263, 269(б), 262.

(творческое):

• Сочинить рассказ, сказку или стихотворение о стране треугольников.

• Составить картинку из различных видов треугольников.