- Учителю
- Факультативные занятия в 7 классе по тема «Элементы комбинаторики»
Факультативные занятия в 7 классе по тема «Элементы комбинаторики»
Факультатив в 7 классе по теме: «Элементы комбинаторики»
Комбинаторика - это раздел математики, в котором исследуются и решаются задачи выбора элементов из исходного множества и расположения их в некоторой комбинации, составленной по заданным правилам.
Если исходное множество состоит из n различных элементов, то при каждом выборе мы будем извлекать из него новый элемент, отличный от всех других - это выбор без повторений.
Если исходное множество состоит из элементов k типов (классов), причём внутри каждого класса элементы неразличимы, то при очередном выборе мы можем извлечь либо новый элемент, либо такой, какой уже встречался при предшествующих извлечениях - это выбор с повторениями.
Иногда модель выбора с повторениями описывают по-другому. Полагают, что исходное множество содержит n различных элементов, но каждый элемент после его извлечения «записывается» в создаваемой комбинации и возвращается обратно в исходное множество. При этом каждый из n элементов может быть извлечён и «записан» неоднократно; число повторений зависит только от числа производимых извлечений. Такую модель называют также выбором с возвращением.
Извлечённые из исходного множества m элементов составляют выборку; из элементов выборки в соответствии с заданными правилами строится (или составляется) комбинация элементов.
Правило умножения. Пусть требуется выполнить одно за другим какие-то m действий. Если первое действие можно выполнить n1 способами, второе действие - n2 способами, третье - n3 способами и так до m-го действия, которое можно выполнить nm способами, то все m действий вместе могут быть выполнены n1 n2 n3… nm способами.
Пример. Четыре мальчика и четыре девочки садятся на 8 расположенных подряд стульев, причём мальчики садятся на места с чётными номерами, а девочки - на места с нечётными номерами. Сколькими способами это можно сделать?
Решение: Первый мальчик может сесть на любое из четырёх чётных мест, второй - на любое из оставшихся трёх мест, третий - на любое из оставшихся двух мест. Последнему мальчику предоставляется всего одна возможность. Согласно правилу умножения, мальчики могут занять 4 места 4321=24 способами. Столько же возможностей имеют и девочки. Таким образом, согласно правилу умножения, мальчики и девочки могут занять все стулья 2424=576 способами.
Ответ: 576 способами.
Правило сложения. Если два действия взаимно исключают друг друга, причём одно из них можно выполнить m способами, а другое - n способами, то выполнить одно любое из этих действий можно m + n способами.
Пример. Имеется 20 тетрадей в линейку и 30 тетрадей в клетку. Необходимо выбрать две тетради одного вида. Сколько способов выбора двух тетрадей возможно, если учитывается порядок выбора тетрадей?
Решение: Условимся первым действием считать выбор тетрадей в линейку, вторым - выбор тетрадей в клетку. По правилу умножения две тетради в линейку можно выбрать 2019=380 способами. Аналогично, две тетради в клетку можно выбрать 3029=870 способами. Согласно условию задачи, следует выбрать две тетради одного вида. Таким образом, должно быть выполнено либо первое, либо второе, но не первое действие, а затем второе. Эти действия не могут быть выполнены одновременно. Поскольку они взаимно исключают друг друга. Поэтому общее число способов выбора тетрадей одного вида равно 380+870=1250.
Ответ: 1250 тетрадей.
Размещением из n элементов по m называется любой выбор m элементов, взятых в определённом порядке из n элементов.
Число размещений из n элементов по m обозначают ![]() .
.
Теорема. Число размещений из n элементов по m равно ![]() т.е.
т.е. ![]()
![]()
Пример. Сколько можно записать четырехзначных чисел, используя без повторения все десять цифр?
Решение: Так как в любом числе важную роль играет порядок входящих в него цифр, то для ответа на поставленный вопрос, очевидно, следует определить число размещений из 10 по 4: ![]() . Однако не все последовательности из 4 цифр представляют собой четырёхзначное число, поскольку среди них есть и такие, у которых на 1-м месте находится 0. Найдём число таких последовательностей. Так как у рассматриваемых последовательностей на 1-м месте уже стоит 0, то следует выбрать ещё 3 цифры из оставшихся 9. найдём число размещений из 9 по 3:
. Однако не все последовательности из 4 цифр представляют собой четырёхзначное число, поскольку среди них есть и такие, у которых на 1-м месте находится 0. Найдём число таких последовательностей. Так как у рассматриваемых последовательностей на 1-м месте уже стоит 0, то следует выбрать ещё 3 цифры из оставшихся 9. найдём число размещений из 9 по 3: ![]() . Таким образом, искомое число четырёхзначных чисел равно разности
. Таким образом, искомое число четырёхзначных чисел равно разности ![]() .
.
Перестановкой из n элементов называется размещение из n элементов по n.
Число перестановок обозначается Рn
Теорема. Число перестановокn различных элементов равно n! т.е. Рn = n!
Пример. Сколькими способами можно расставить девять различных книг на полках, чтобы определённые четыре книги стояли рядом?
Решение: Будем считать выделенные книги за одну книгу. Тогда для шести книг существует Р6=6!=720 перестановок. Однако 4 определённые книги можно переставить между собой Р4=4!=24 способами. По правилу умножения имеем Р6Р4=72024=17280.
Сочетанием из n элементов по m называется любой выбор m элементов, взятых из n элементов.
Число сочетаний из n элементов по m обозначают и вычисляют по формуле:
![]()
![]() , которую можно записать также в виде:
, которую можно записать также в виде: ![]()
Теорема. Число сочетаний из n элементов по m равно т.е. ![]()
![]()
Пример: Сколькими способами можно группу из 12 человек разбить на две подгруппы, в одной из которых должно быть не более пяти, а во второй - не более девяти человек?
Решение: Первая подгруппа может состоять либо из трёх, либо из четырёх, либо из пяти человек. Подгруппу из трёх человек можно выбрать ![]() способами. Подгруппу из четырёх человек можно выбрать
способами. Подгруппу из четырёх человек можно выбрать ![]() способами, а подгруппу из пяти человек -
способами, а подгруппу из пяти человек - ![]() способами. Учитывая, что выбор первой подгруппы однозначно определяет вторую, найдём по правилу сложения искомое число способов:
способами. Учитывая, что выбор первой подгруппы однозначно определяет вторую, найдём по правилу сложения искомое число способов: ![]() .
.
Ответ: 1507 способов.
Теорема. Имеет место равенство ![]()
Пример. Сколько существует вариантов опроса 11 учащихся на одном занятии, если ни один из них не будет подвергнут опросу дважды и на занятии может быть опрошено любое количество учащихся, причём порядок, в котором опрашиваются учащиеся, безразличен?
Решение: Преподаватель может не спросить ни одного из 11 учащихся, что является одним из вариантов. Этому случаю соответствует ![]() . Преподаватель может опросить только одного из учащихся. Таких вариантов
. Преподаватель может опросить только одного из учащихся. Таких вариантов ![]() . Если преподаватель будет опрашивать двух учащихся, то число вариантов опроса равно
. Если преподаватель будет опрашивать двух учащихся, то число вариантов опроса равно ![]() . Для опроса трёх учащихся существует
. Для опроса трёх учащихся существует ![]() вариантов и т.д. Наконец, могут быть опрошены все учащиеся. Число вариантов в этом случае равно
вариантов и т.д. Наконец, могут быть опрошены все учащиеся. Число вариантов в этом случае равно ![]() . Тогда по правилу сложения число всех возможных вариантов опроса равно
. Тогда по правилу сложения число всех возможных вариантов опроса равно ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() …
…![]()
![]() . С другой стороны, для каждого из учащихся существует две возможности: он будет опрошен или не опрошен на данном занятии. Другими словами, каждую из 11 операций, заключающихся в том, что каждый ученик будет либо опрошен, либо не опрошен, можно выполнить по правилу умножения 222…2=211 способами, что и следовало ожидать, так как
. С другой стороны, для каждого из учащихся существует две возможности: он будет опрошен или не опрошен на данном занятии. Другими словами, каждую из 11 операций, заключающихся в том, что каждый ученик будет либо опрошен, либо не опрошен, можно выполнить по правилу умножения 222…2=211 способами, что и следовало ожидать, так как ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() …
…![]()
![]()
![]() .
.
Задачи.
Правило умножения
-
В меню столовой предложено на выбор 5 первых, 8 вторых и 4 третьих блюда. Сколько различных вариантов обедов, состоящих из одного первого, одного второго и одного третьего блюда, можно составить из предложенного меню?
Решение: Согласно правилу умножения таких обедов можно составить 584 = 160.
Ответ: 160 вариантов обедов.
-
Миша забыл вторую и последнюю цифру пятизначного номера телефона друга. Какое наибольшее число звонков предстоит сделать Мише, если он решил перепробовать комбинации всех забытых цифр, чтобы в результате дозвониться до друга?
Решение: Второй и последней цифрой могут быть все 10 цифр. По правилу умножения получаем 1010=100.
Ответ: 100 звонков.
4. Девятиклассники Миша, Дима, Антон и Саша побежали на перемене к теннисному столу, за которым уже шла игра. Сколькими способами подбежавшие к столу четверо девятиклассников могут занять очередь для игры в настольный теннис?
Решение: Первым в очередь мог встать любой девятиклассник, вторым - любой из оставшихся троих, третьим - любой из оставшихся двоих и четвёртым - девятиклассник, подбежавший последним. По правилу умножения у четверых ребят существует 4321=24 способа занять очередь.
Ответ: 24 способа.
5. Здание школы имеет 5 запасных выходов. Сколькими способами можно войти и выйти из здания школы?
Решение: По правилу умножения получаем 55=25 способов.
Ответ: 25 способов.
6. В городских соревнованиях по футболу участвовало 5 команд. Каждая
команда провела с каждой из остальных по одной игре на своём поле и по
одной игре на поле соперника. Сколько всего игр было сыграно?
Решение: Порядок выбора пары не имеет значения. Для каждой игры принимающую команду можно выбрать 5 способами, а команду гостей 4 способами; по правилу умножения общее количество игр равно 54=20 игр
Ответ: 20 игр.
7. В гардеробе у Алёши имеются брюки трёх цветов, свитера двух расцветок и ботинки двух цветов. Сколько существует всевозможных цветовых сочетаний брюк, свитера и ботинок у Алёши?
Решение: По правилу умножения получаем 322=12 сочетаний.
Ответ: 12 сочетаний.
8. Одновременно происходят выборы президента школьной детско-юношеской организации «СОТУР» и его заместителя. На должность президента выставили свои кандидатуры Лапина Юля, Губенко Юля, Осадчук Женя, а на должность заместителя - Малеванова Кристина, Явон Даша и Русалеева Даша. Сколько различных исходов выборов существует? В скольких вариантах будет кандидатура Малевановой Кристины?
Решение: По правилу умножения число различных исходов выборов равно 33=9. Кандидатура Малевановой Кристины будет в 3 вариантах.
Ответ: 9 исходов; 3 варианта.
9. У Любы есть любимый костюм, в котором она ходит в школу. Она надевает к нему белую, голубую, розовую или красную блузку, а в качестве «сменки» берёт босоножки или туфли. Кроме того, у Любы есть три разных бантика, подходящих ко всем блузкам. а) Сколько существует вариантов Любиной одежды? б) Сколько дней Люба сможет выглядеть по-новому в этом костюме? в) Сколько дней она будет ходить в туфлях? г) Сколько дней она будет ходить в красной блузке и босоножках?
Решение: а) По правилу умножения получаем: 423=24 варианта. б) по-новому будет выглядеть 24 дня. в) 12 дней (половина вариантов). г) 3 дня (так как будут меняться только бантики).
Ответ: а) 24 варианта; б) 24 дня; в) 12 дней; г) 3 дня.
10. Составляя расписание уроков на понедельник для 9 «Б» класса, завуч хочет первым уроком поставить либо физику, либо алгебру, а вторым - либо русский язык, либо литературу, либо историю, либо географию. Сколько существует вариантов составления расписания на первые два урока?
Решение: По правилу умножения получаем: 42=8 вариантов.
Ответ: 8 вариантов.
11. У Светланы три юбки и 5 кофт, удачно сочетающихся по цвету. Сколько различных комбинаций из юбок и кофт имеется у Светланы?
Решение: По правилу умножения получаем: 35=15 комбинаций.
Ответ: 15 комбинаций.
12. Стас решил пойти на новогодний карнавал в костюме мушкетёра. В ателье проката ему предложили на выбор различные по фасону и цвету предметы: 3 пары брюк, 4 камзола, 3 шляпы, 2 пары сапог. Сколько различных карнавальных костюмов можно составить из этих предметов?
Решение: Общее количество предметов по правилу умножения равно: 3432=72.
Ответ: 72 различных костюма.
13. Завуч составляет расписание уроков. В пятницу в 9 «Г» классе должно быть 6 уроков, причём обязательно один сдвоенный урок - алгебра. Сколько различных вариантов расписания уроков может составить завуч на пятницу, если 4 оставшихся урока она комбинирует из литературы, истории, биологии и физики?
Решение: Будем рассматривать сдвоенный урок как один урок, тогда всего нужно поставить в расписание 5 уроков. Первый урок можно выбрать из 5 вариантов, второй - из 4 вариантов, третий - из 3 вариантов, четвёртый - из 2 вариантов, а пятым поставить оставшийся урок. Общее число вариантов равно 54321=120 вариантов.
Ответ: 120 вариантов.
14. На зачёте по алгебре будет пять задач - по одной из каждой пройденной темы. Задачи будут взяты из общего списка по 10 задач в каждой теме, а всего было пройдено 5 тем. При подготовке к зачёту Вова решил только по 8 задач в каждой теме. Найдите: а) общее число всех возможных вариантов зачётной работы; б) число тех вариантов, в которых Вова умеет решать все пять задач;
в) число тех вариантов, в которых Вова не сможет решить ни одной задачи;
г) число тех вариантов, в которых Вова умеет решать все задачи, кроме первой.
Решение: а) Первая задача может быть выбрана 10 способами, вторая тоже 10 (из задач другой темы), третья, четвёртая и пятая задачи также могут быть выбраны 10 способами каждая; по правилу умножения общее число всех возможных вариантов зачётной работы равно 1010101010=100000. б) Число вариантов, в которых Вова умеет решать все пять задач равно 88888=32768. в) Число вариантов, в которых Вова не сможет решить ни одной задачи равно 22222=32. г) Число тех вариантов, в которых Вова умеет решать все задачи, кроме первой, равно 28888=8192.
Ответ: а) 100000; б) 32768; в) 32; г) 8192.
Перестановки
1. Сколькими способами Дима и Вова могут занять 2 места за одной двухместной партой?
1 решение: Присвоим каждому месту за партой номер. Тогда Дима и Вова могут занять места за партой такими способами: 1. Дима. 2. Вова или 1. Вова.
2. Дима. Других вариантов нет.
2 решение: Количество различных способов равно числу перестановок из 2 элементов: Р2 = 2! = 12 = 2 способа
Ответ: 2 способа.
2. Олеся, Оксана и Юля купили билеты на концерт симфонического оркестра на 1, 2 и 3-е места первого ряда. Сколько существует способов размещения девочек на эти места?
Решение: Количество различных способов равно числу перестановок из 3 элементов: Р3 = 3! = 123 = 6 способов
Ответ: 6 способов.
-
Из трёх стаканов сока - яблочного, сливового и абрикосового - Коля решил последовательно выпить два. Перечислите все варианты, которыми это можно сделать.
Ответ: 1) яблочный, сливовый; 2) сливовый, яблочный; 3) яблочный, абрикосовый; 4) абрикосовый, яблочный; 5) сливовый, абрикосовый;
6) абрикосовый, сливовый.
4. Сергей, Игорь и Миша могут занять 1-е, 2-е и 3-е призовые места в соревнованиях по шахматам. Перечислить всевозможные последовательности из имён мальчиков, где порядковый номер в последовательности соответствует занятому мальчиком месту в соревнованиях. Подсчитать их количество.
Решение: Сначала выбираем одного на первое место, а двух других меняем местами, потом берём на первое место другого и т.д.: СИМ; СМИ; ИСМ; ИМС; МСИ; МИС. Всего 6 вариантов расположения.
Ответ: 6 вариантов.
5. У Влада на обед - первое, второе, третье и пирожное. Он обязательно начнёт с пирожного, а всё остальное съест в произвольном порядке. Найдите число возможных вариантов обеда.
Решение: После пирожного Влад может выбрать любое из трёх блюд, затем - из двух, и закончит оставшимся. Общее число возможных вариантов обеда:
321=6.
Ответ: 6.
6. Четыре друга купили билеты в кино: на 1-е и 2-е места в первом ряду и на 1-е и 2-е места во втором ряду. Сколькими способами друзья могут занять эти 4 места в кинотеатре?
Решение: Четыре друга могут занять 4 разных места Р4=4!=1234=24 различными способами.
Ответ: 24 способа.
7. Сколькими способами 9 учащихся могут встать в очередь в школьном буфете?
Решение: Присвоим каждому учащемуся номер (от 1 до 9). Тогда каждый способ расположения этих учащихся в очереди будет представлять собой последовательность из 9 цифр, порядок которых может меняться. Количество способов, которыми 9 учащихся могут встать в очередь равно: Р9=9!=123456789=362880.
Ответ: 362880 способов.
8. Ольга помнит, что телефон подруги оканчивается цифрами 5, 7, 8, но забыла, в каком порядке эти цифры следуют. Укажите наибольшее число вариантов, которые ей придётся перебрать, чтобы дозвониться подруге.
Решение: Три последних цифры телефонного номера могут быть расположены в одном из Р3=3!=123=6 возможных порядков, из которых только один верный. Ольга может сразу набрать верный вариант, может набрать его третьим, и т.д. Наибольшее число вариантов ей придётся набрать, если правильный вариант окажется последним, т.е. шестым.
Ответ: 6 вариантов.
9. Семь мальчиков, в число которых входят Сергей и Игорь, становятся в ряд. Найдите число возможных комбинаций, если:
а) Сергей должен находиться в конце ряда;
б) Сергей должен находиться в начале ряда, а Игорь - в конце ряда;
в) Сергей и Игорь должны стоять рядом.
Решение: а) Всего 7 мальчиков на 7 местах, но один элемент фиксирован, не переставляется (Сергей находится в конце ряда). Число возможных комбинаций при этом равно числу перестановок 6 мальчиков, стоящих пред Сергеем: Р6=6!=123456=720. б) Два элемента фиксированы. Число возможных комбинаций равно числу перестановок 5 мальчиков, стоящих между Сергеем и Игорем: Р5=5!=12345=120. в) Воспользуемся приёмом «склеивания» элементов. Пусть Сергей и Игорь стоят рядом в порядке СИ. Будем рассматривать эту пару как единый элемент, представляемый с другими пятью элементами. Число возможных комбинаций тогда будет Р6=6!=123456=720. пусть теперь Сергей и Игорь стоят рядом в порядке ИС. Тогда получим ещё Р6=6!=720 других комбинаций. Общее число комбинаций, в которых Сергей и Игорь стоят рядом (в любом порядке) равно 720+720=1440.
Ответ: а) 720; б) 120; в) 1440 комбинаций.
10. Одиннадцать футболистов школьной команды строятся перед началом
матча. Первым становится капитан, вторым - вратарь, а остальные - случайным образом. Сколько существует способов построения?
Решение: После капитана и вратаря третий игрок может выбрать любое из 9 оставшихся мест, следующий - из 8, и т.д. Общее число способов построения по правилу умножения равно: 1987654321=362880, или 1 Р9=9!=362880.
Ответ: 362880.
11. В расписании на понедельник шесть уроков: алгебра, геометрия, биология, история, химия, физкультура. Сколькими способами можно составить расписание уроков на этот день так, чтобы два урока математики стояли рядом?
Решение: Всего 6 уроков, из них два урока математики должны стоять рядом. «Склеиваем» два элемента (алгебра и геометрия) сначала в порядке АГ, затем в порядке ГА. При каждом варианте «склеивания» получаем: Р5=5!=12345=120 вариантов расписания. Общее число способов составить расписание равно 120+120=240.
Ответ: 240 способов.рвое место, а двух других меняче место, а двух других менячяем местами, потом берём на первое место другого и т.д.:ет занятому
Сочетания
1. Имеется три предмета: карандаш, тетрадь и линейка. Сколькими способами из этих канцелярских принадлежностей можно выбрать 2 предмета?
1 решение: Два предмета можно выбрать так: берём поочерёдно один предмет из ряда (кроме последнего) и добавляем к нему по одному предметы, следующие за ним в ряду: карандаш, тетрадь; карандаш, линейка; тетрадь, линейка. Получаем 3 различных варианта.
2 решение: ![]() способа.
способа.
Ответ: 3 способа.
2. В школьной столовой имеются помидоры, огурцы и лук. Сколько различных салатов можно приготовить, если в каждый из них должны входить в равных долях 2 различных вида овощей? Записать все сочетания овощей в составленных салатах.
Решение: Расположим данные овощи по порядку: помидоры, огурцы, лук. Запишем все сочетания овощей в салатах. Будем брать поочерёдно каждый овощ (кроме последнего) и добавлять к нему по одному, только из последующих, поскольку порядок выбора не важен: 1) помидоры, огурцы;
2) помидоры, лук; 3) огурцы, лук.
Ответ: 3 вида салатов.
3. Володя идёт на день рождения к одноклассникам, двойняшкам Диме и Ивану. Он хочет подарить каждому из них по мячу. В магазине остались для продажи только 3 мяча разных цветов: белый, чёрный и пятнистый. Сколькими способами, купив 2 мяча, Володя может сделать подарки братьям?
Решение: По условию задачи предусмотрены два последовательных выбора: сначала Володя выбирает 2 мяча из трёх, имеющихся в магазине, а потом решает, какому из братьев-двойняшек подать каждый из купленных мячей. Два мяча из трёх можно выбрать тремя способами (![]() способа). После этого каждую выбранную пару можно подарить двумя способами (
способа). После этого каждую выбранную пару можно подарить двумя способами (![]() способа) (порядок важен). Тогда по правилу умножения искомое число способов равно
способа) (порядок важен). Тогда по правилу умножения искомое число способов равно ![]() способов.
способов.
Ответ: 6 способов.
4. В магазине продают кепки трёх цветов: белые, красные и синие. Наташа и Лена покупают себе по одной кепке. Сколько существует различных вариантов покупок для этих девочек?
Решение: В магазине продаются кепки трёх видов, поэтому девочки могут купить кепки одинаковых цветов, т.е. возможен выбор с повторением. Порядок выбора также важен и должен учитываться. Лена может сделать выбор ![]() способами и Наташа также 3 способами. По теореме умножения получаем:
способами и Наташа также 3 способами. По теореме умножения получаем: ![]() вариантов.
вариантов.
Ответ: 9 вариантов.
5. Сколько существует способов выбрать троих ребят из 11 желающих дежурить по школе?
Решение: Количество сочетаний из 11 по 3 (порядок выбора не имеет значения) равно: ![]() .
.
Ответ: 165 способов.
6. В 9 «Г» классе 5 человек успешно занимаются математикой. Сколькими способами можно выбрать из них двоих для участия в математической олимпиаде?
Решение: Выбираем 2 учащихся из 5, порядок выбора не имеет значения (оба выбранных пойдут на олимпиаду как полностью равноправные); количество способов выбора равно числу сочетаний из 5 по 2: ![]() способов.
способов.
Ответ: 10 способов.
7. Учащимся дали список из 10 книг, которые рекомендуется прочитать во время каникул. Сколькими способами ученик может выбрать из них 6 книг?
Решение: Выбор 6 из 10 без учёта порядка: ![]() способов.
способов.
Ответ: 210 способов.
8. В 9 «Г» классе учатся 16 мальчиков и 10 девочек. Для уборки территории требуется выделить четырёх мальчиков и трёх девочек. Сколькими способами можно это сделать?
Решение: Нужно сделать два выбора: 4 мальчиков из 16 (всего способов ![]() ) и 3 девочек из 10 (всего способов
) и 3 девочек из 10 (всего способов ![]() ); порядок выбора значения не имеет (все идущие на уборку равноправные). Каждый вариант выбора мальчиков может сочетаться с каждым выбором девочек, поэтому по правилу умножения общее число способов выбора равно:
); порядок выбора значения не имеет (все идущие на уборку равноправные). Каждый вариант выбора мальчиков может сочетаться с каждым выбором девочек, поэтому по правилу умножения общее число способов выбора равно: ![]()
![]() =
=![]() способов.
способов.
Ответ: 218400 способов.
9. В библиотеке Кате предложили на выбор из новых поступлений 10 книг и 4 журнала. Сколькими способами она может выбрать из них 3 книги и 2 журнала?
Решение: Нужно сделать два выбора: 3 книги из 10 (![]() способов) и 2 журнала из 4 (
способов) и 2 журнала из 4 (![]() способов); порядок выбора не имеет значения. Каждый выбор книг может сочетаться с каждым выбором журналов, поэтому общее число способов выбора по правилу умножения равно:
способов); порядок выбора не имеет значения. Каждый выбор книг может сочетаться с каждым выбором журналов, поэтому общее число способов выбора по правилу умножения равно: ![]()
![]() =
=![]() способов.
способов.
Ответ: 720 способов.
10. В 9 «Б» классе учатся 22 учащихся, в 9 «В» - 19 учащихся, а в 9 «Г» - 26 учащихся. Для работы на пришкольном участке надо выделить трёх учащихся из 9 «Б» класса, двух - из 9 «В» и одного - из 9 «Г». Сколько существует способов выбора учащихся для работы на пришкольном участке?
Решение: Выбор из трёх совокупностей без учёта порядка, каждый вариант выбора из первой совокупности (![]() ) может сочетаться с каждым вариантом выбора из второй (
) может сочетаться с каждым вариантом выбора из второй (![]() ) и с каждым вариантом выбора третьей (
) и с каждым вариантом выбора третьей (![]() ); по правилу умножения получаем:
); по правилу умножения получаем: ![]()
![]()
![]() =
=![]() способов выбора учащихся.
способов выбора учащихся.
Ответ: 32522490 способов.
11. По списку в 9 «Г» классе 16 мальчиков и 10 девочек. Нужно выбрать двух дежурных по классу. Сколькими способами это можно сделать: а) при условии. Что пару обязательно должны составить мальчик и девочка; б) без указанного условия?
Решение: а) Выбираем 1 мальчика из 16 и 1 девочку из 10; общее число способов выбора пары: ![]() . б) Выбрать 2 дежурных из 16+10=26 учащихся класса (без учёта порядка) можно:
. б) Выбрать 2 дежурных из 16+10=26 учащихся класса (без учёта порядка) можно: ![]() способами.
способами.
Ответ: а) 160; б) 325.
12. По списку в 9 «Г» классе 16 мальчиков и 10 девочек. Нужно выбрать двух дежурных по классу. Нужно выделить группу из трёх человек для посещения заболевшего одноклассника. Сколькими способами это можно сделать, если: а) все члены этой группы должны быть девочками; б) все члены этой группы должны быть мальчиками; в) в группе должны быть 1 девочка и 2 мальчика; г) в группе должны быть 2 девочки и 1 мальчик.
Решение: а) Выбрать 3 девочек из 10 имеющихся без учёта порядка можно
![]() различными способами. б) Выбрать 3 мальчиков из 16
различными способами. б) Выбрать 3 мальчиков из 16
имеющихся, без учёта порядка, можно ![]() различными способами. в) Выбрать 1 девочку из 10, а затем 2 мальчика из 16 без учёта порядка можно
различными способами. в) Выбрать 1 девочку из 10, а затем 2 мальчика из 16 без учёта порядка можно ![]() различными способами. г) Выбрать 2 девочек из 10, а затем 1 мальчика из 16 без учёта порядка можно
различными способами. г) Выбрать 2 девочек из 10, а затем 1 мальчика из 16 без учёта порядка можно ![]() различными способами.
различными способами.
Ответ: а) 120; б) 560; в) 1200; г) 720.
Подсчёт вариантов
1. Сколькими различными способами можно назначить двух ребят на
дежурство по столовой, если в классе 22 учащихся?
Решение: Назначая двух дежурных по столовой, мы не учитываем порядок выбора пары из учащихся данного класса. Так как в классе 22 учащихся, то первого дежурного можно выбрать из 22 учащихся, а второго - из 21 учащегося. Так как порядок выбора не учитывается, то получаем 2221:2=231 способ.
Ответ: 231 способ
2. В шахматном турнире участвуют 9 старшеклассников. Каждый из них
сыграл с каждым по одной партии. Сколько всего партий было сыграно?
Решение: Поскольку каждая пара участников играла между собой только один раз, порядок выбора не имеет значения. Выбрать первого участника партии можно 9 способами, а второго - 8 оставшимися способами; по теореме умножения всего можно образовать 98=72 пары, но в это число каждая пара входит дважды: сначала Дроздов-Гончаров, затем Гончаров-Дроздов. Поскольку порядок выбора не имеет значения, то общее количество партий
равно 98:2=36 партий.
Ответ: 36 партий.
3. При встрече 8 друзей обменялись рукопожатиями. Сколько всего было сделано рукопожатий?
Решение: Порядок выбора не имеет значения: если Агапеев пожимает руку Зайцеву, то одновременно и Зайцев пожимает руку Агапееву, поэтому общее количество рукопожатий (пар) равно 87:2=28.
Ответ: 28 рукопожатий.
4. У Марины пять подруг: Наташа, Оля, Кристина, Ксения и Светлана. Она решила двух из них пригласить в кино. Сколько существует вариантов?
Решение: По условию ясно, что порядок выбора значения не имеет. По правилу умножения всего 54=20 вариантов выбора, но так как порядок выбора не имеет значения, то получаем: 20:2=10 вариантов.
Ответ: 10 вариантов.
5. Учащиеся 9 «Г» класса решили обменяться фотографиями. Сколько фотографий для этого потребуется, если в классе 26 учащихся?
Решение: считаем, что в каждой паре происходит передача одновременно двух фотографий, т.е. учащиеся в паре равноправны, неразличимы. Тогда при образовании пар порядок выбора не имеет значения: количество таких пар равно 2625:2=325.
Ответ: 325 фотографий.
Разбиение на две группы
1. В списке класса для изучения английского языка 15 человек. Сколько существует вариантов присутствия (отсутствия) этих людей на занятии?
Решение: Задачу решаем разбиением на две группы: присутствующие и отсутствующие. Разбиение на группы однозначно определяется составом элементов в одной из групп (не попавшие в первую группу элементы автоматически образуют вторую группу). Подсчитаем все варианты составления одной группы. Согласно правилу умножения комбинаций (вариантов) из «присутствующих» или «отсутствующих» будет 215.
Ответ: 215= 32768 вариантов
2. Имеется 6 карандашей шести разных цветов. Сколькими способами эти карандаши могут быть распределены между двумя школьниками?
Решение: Задача сводится к подсчёту числа всевозможных способов разбиения шести различных элементов (карандашей) на две группы. Это число равно 26 = 64.
Ответ: 64 способами.
3. Каждая из 5 подруг собирается вечером пойти либо в кино, либо на каток. Сколькими различными способами эти пять подруг смогли бы провести вечер?
Решение: Подсчитаем все варианты составления одной группы. Согласно правилу умножения комбинаций (вариантов) из «посетивших кинотеатр» или «посетивших каток» будет 25.
Ответ: 25= 32 варианта.
4. У Антона шесть друзей. Он может пригласить в гости одного или нескольких из них. Определите общее число возможных вариантов.
Решение: Разобьём множество из 6 элементов на две группы: приглашённых и неприглашённых. Расположим всех друзей в ряд, и под именем каждого друга будем писать 0, если этот друг не приглашён, и 1, если он приглашен. Получим шестизначные наборы нулей и единиц. Общее количество таких наборов по правилу умножения равно: 26=64, но среди этих наборов есть один, состоящий из 6 нулей, т.е. никто не приглашён. Этот набор нужно исключить (по условию задачи число приглашённых не менее одного), в результате получим: 64-1=63.
Ответ: 63 варианта.
Размещения
1. Из трёх стаканов сока - ананасового, брусничного и виноградного - Костя решил последовательно выпить два. Сколькими способами это можно сделать?
Решение: Это задача о выборе двух элементов из трёх с учётом порядка выбора. Число способов равно ![]()
![]() способов
способов
Ответ: 6 способов.
2. Сколькими способами могут быть заняты первое, второе и третье места (по одной команде на место) на соревнованиях по гимнастике, в которых участвуют 6 команд?
Решение: Это задача о выборе трёх элементов из шести с учётом порядка выбора. ![]() .
.
Ответ: 120 способов.
3. Из 26 учащихся класса надо выбрать старосту и его заместителя. Сколькими способами это можно сделать?
Решение: Из 26 учащихся выбираем 2, причём порядок выбора имеет значение. Количество способов выбора равно ![]()
![]() способов.
способов.
Ответ: 650 способов.
4. Сколькими способами могут занять первое, второе и третье места 8 участниц финального забега на дистанции 100 м?
Решение: Выбор из 8 по 3 с учётом порядка: ![]()
![]() способов.
способов.
Ответ: 336 способов.
5. На соревнованиях по лёгкой атлетике нашу школу представляла команда из 10 спортсменов. Сколькими способами тренер может определить, кто из них побежит в эстафете 4100 м на первом, втором, третьем и четвёртом этапах?
Решение: Выбор из 10 по 4 с учётом порядка: ![]()
![]() способов.
способов.
Ответ: 5040 способов.
6. Сколькими способами могут быть распределены первая, вторая и третья премии между 13 участниками конкурса?
Решение: Выбираем трёх призёров из 13 участников конкурса с учётом порядка (кому какая премия): ![]()
![]() способов.
способов.
Ответ: 1716 способов.
7. Сколькими способами 6 девятиклассников, сдающих экзамен, могут занять места в кабинете, в котором стоит 15 столов?
Решение: Выбираем 6 столов для девятиклассников из 15 имеющихся: порядок выбора учитывается (кто сидит у окна, кто около преподавателя, и т.п.): ![]()
![]() способов.
способов.
Ответ: 3603600 способов.
8. Сколько команд участвовало в финале первенства города по хоккею, если каждая команда сыграла с каждой из остальных по одной игре на своём поле и по одной игре на поле соперника, причём всего было сыграно 30 игр?
Решение: Поскольку каждая пара команд сыграла между собой по две игры (на своём и чужом поле), то выбор пары осуществляется с учётом порядка, т.е. составляются всевозможные размещения из n по 2. По условию задачи ![]() =30, отсюда n(n-1) = 65, n = 6.
=30, отсюда n(n-1) = 65, n = 6.
Ответ: 6 команд.
9. В классе 30 учащихся. Сколькими способами можно выбрать из класса команду из 4 учащихся для участия в олимпиаде по истории, литературе, русскому и английскому языкам?
Решение: Искомые команды будут отличаться между собой или учащимися, или их порядком, который указывает, на какую олимпиаду пойдёт ученик. Поэтому искомое число равно числу размещений из 30 по 4 и по формуле получаем: ![]() способов.
способов.
Ответ: 657720 способов.
10. Учащиеся 9 класса изучают 14 предметов. Сколькими способами можно составить расписание уроков на один день так, чтобы было 6 различных уроков?
Решение: Выбираем 6 предметов из 14 имеющихся с учётом выбора предметов. Получаем ![]() способов.
способов.
Ответ: 2162160 способов.
Комбинированные задачи
1. В шахматном кружке занимаются 16 человек. Сколькими способами тренер может выбрать из них для предстоящего турнира: а) команду из четырёх человек; б) команду из четырёх человек, указав при этом, кто из членов команды будет играть на первой, второй, третьей и четвёртой доске?
Решение: а) Выбираем 4 шахматистов из 16 без указания порядка; количество способов ![]() . б) Выбираем 4 шахматистов из 16 с указанием порядка их расположения в команде; количество способов
. б) Выбираем 4 шахматистов из 16 с указанием порядка их расположения в команде; количество способов ![]() .
.
Ответ: а) 1820 способов; б) 43680 способов.
2. Из 20 вопросов к экзамену Саша 12 вопросов выучил, 5 совсем не смотрел, а в остальных что-то знает, а что-то не знает. На экзамене в билете будет три вопроса.
а) Сколько существует вариантов билетов?
б) Сколько из них тех, в которых Саша знает все вопросы?
в) Сколько из них тех, в которых есть вопросы всех трёх типов?
г) Сколько из них тех, в которых Саша выучил большинство вопросов?
Решение: а) для составления билета выбираются 3 вопроса из 20 имеющихся, при этом порядок выбора значения не имеет. Общее число вариантов билетов равно: ![]() . б) Саша выучил 12 вопросов; из этих вопросов можно составить
. б) Саша выучил 12 вопросов; из этих вопросов можно составить ![]() разных билетов. в) Количество билетов, в которых есть вопросы всех трёх типов равно: 12 вариантов выбора вопроса, который выучил, умножить на 5 вариантов выбора вопроса, который совсем не смотрел, и умножить на 20-12-5=3 варианта выбора вопроса, в котором что-то знает, всего 1253=180 разных билетов. г) Билеты, в которых Саша выучил большинство вопросов, это билеты, в которых он знает два или три вопроса. Билеты, в которых Саша выучил все три вопроса - 220 (см.пункт б). Найдём сколько есть билетов, в которых Саша выучил 2 вопроса: выбрать 2 вопроса из 12 выученных можно
разных билетов. в) Количество билетов, в которых есть вопросы всех трёх типов равно: 12 вариантов выбора вопроса, который выучил, умножить на 5 вариантов выбора вопроса, который совсем не смотрел, и умножить на 20-12-5=3 варианта выбора вопроса, в котором что-то знает, всего 1253=180 разных билетов. г) Билеты, в которых Саша выучил большинство вопросов, это билеты, в которых он знает два или три вопроса. Билеты, в которых Саша выучил все три вопроса - 220 (см.пункт б). Найдём сколько есть билетов, в которых Саша выучил 2 вопроса: выбрать 2 вопроса из 12 выученных можно ![]() разными способами; третий вопрос можно выбрать из 8 остальных вопросов (8 вариантов выбора). По правилу умножения количество билетов, в которых Саша выучил два вопроса равно
разными способами; третий вопрос можно выбрать из 8 остальных вопросов (8 вариантов выбора). По правилу умножения количество билетов, в которых Саша выучил два вопроса равно ![]() . Таким образом, количество билетов, в которых Саша выучил большинство вопросов, по комбинаторному правилу сложения равно 220+528=748.
. Таким образом, количество билетов, в которых Саша выучил большинство вопросов, по комбинаторному правилу сложения равно 220+528=748.
Ответ: а) 1140; б) 220; в) 180; г) 748.
Элементы теории вероятностей
События
В жизни под событием понимают любое явление, которое происходит или не происходит. Событиями являются и результаты испытаний (опытов), наблюдений и измерений. Все события можно разделить на невозможные, достоверные и случайные.
Невозможным называют событие, которое в данных условиях произойти не может.
Например: а) Петя родился 30 февраля;
б) вода в чайнике закипела при температуре 50С.
Достоверным называют событие, которое в данных условиях обязательно произойдёт.
Например: а) после урока наступит перемена;
б) после воскресенья наступит будний день.
Случайным называют событие, которое в данных условиях может произойти, а может и не произойти.
Например: а) при телефонном звонке абонент оказался занят;
б) день рождения двух моих друзей - 15 марта.
Два события, которые в данных условиях могут происходить одновременно, называют совместными, а те, которые не могут происходить одновременно, -несовместными.
Например, события «пошёл дождь» и «наступило утро» являются совместными, а события «наступило утро» и «наступила ночь» - несовместными.
События называются равновозможными, если по условию испытания нет оснований считать какое-либо из них более возможным, чем любое другое.
Рассмотрим группы событий:
-
«появление орла» и «появление решки» при одном бросании монеты;
-
«появление 1 очка», «появление 2 очков», …, «появление 6 очков» при одном бросании игральной кости;
-
«падение бутерброда маслом вверх» и «падение бутерброда маслом вниз»;
-
«изъятие из набора домино дубля» и «изъятие из набора домино костяшки с разными очками».
В примерах 1 и 2 нет оснований полагать, что в наступлении одного из событий есть какое-то преимущество (если монета и кубик правильные). Это равновозможные события. Часто равновозможность событий удаётся установить из соображений симметрии.
Примеры 3 и 4 демонстрируют образцы неравновозможных событий. Действительно, бутерброд чаще падает маслом вниз из-за того, что после намазывания хлеба маслом центр тяжести бутерброда смещается из центра его симметрии в сторону слоя масла. Дублей в наборе домино (пример 4) всего 7, а остальных костяшек 21.
Событие ![]() называется событием, противоположным событию А, если оно происходит, когда не происходит событие А.
называется событием, противоположным событию А, если оно происходит, когда не происходит событие А.
Пример. Событию «все спортсмены команды завоевали призовые места» противоположным является событие «хотя бы один из спортсменов команды не занял призовое место».
Классическое определение вероятности
В повседневной жизни в разговоре часто используется слово «вероятный». Например, «к вечеру, вероятно, пойдёт дождь», «это невероятный случай», «вероятнее всего он опоздает». При употреблении этого слова интуитивно оценивается возможность наступления того или иного события. Можно сказать, что одно событие наступает чаще, чем другое. В этом случае говорят, что оно более возможно, т.е. его наступление более вероятно. Естественно. При такой оценке человеку помогает здравый смысл и жизненный опыт.
Вероятность события - это численная мера объективной возможности его появления.
Событие А называется благоприятствующим событию В, если появление события А влечёт за собой появление события В.
Пример. Событие А={выбито 4 очка} является благоприятствующим событию В={выбито менее 5 очков}.
Вероятность Р(А) наступления события А вычисляется как отношение числа исходов, благоприятствующих наступлению события, к числу всех исходов испытания.
Если N - число всех исходов испытания, а М - число исходов, благоприятствующих событию А, то ![]() .
.
Пример. В классе 30 учащихся. Из них 12 мальчиков, остальные девочки. Известно, что к доске должны быть вызваны двое учащихся. Какова вероятность, что это девочки?
Решение: Обозначим событие, вероятность которого надо найти, буквой А. Очевидно, что по условию задачи порядок вызова к доске не играет роли, поэтому N=![]() . Найдём теперь число М благоприятствующих исходов. Для этого следует определить число способов выбора двух девочек из 18. Оно равно
. Найдём теперь число М благоприятствующих исходов. Для этого следует определить число способов выбора двух девочек из 18. Оно равно
![]() . По определению вероятности
. По определению вероятности 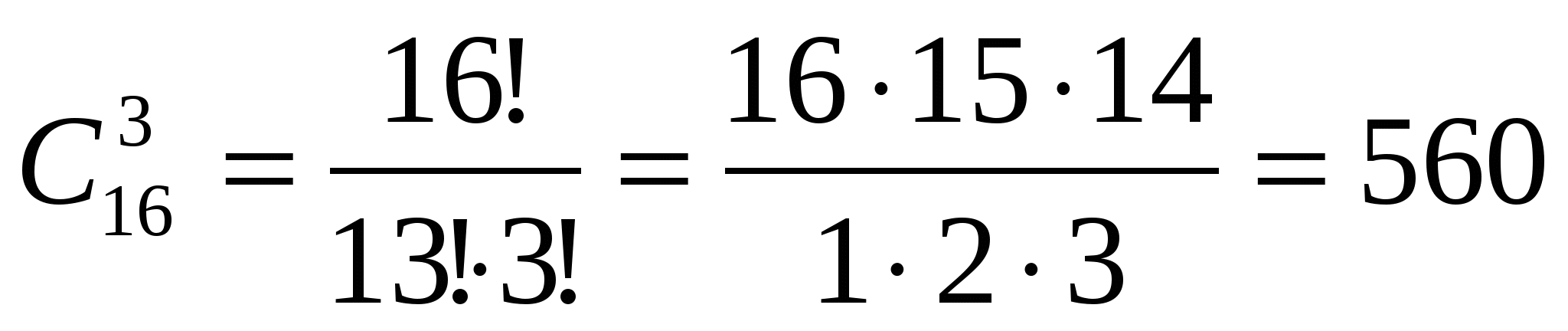 .
.
Свойства вероятности
1. Вероятность достоверного события равна 1: ![]() .
.
2. Вероятность невозможного события равна 0: ![]()
Теорема. Сумма вероятностей противоположных событий равна 1: ![]() .
.
Вероятность противоположного события находится по формуле: ![]() .
.
Пример. Вероятность попадания некоторым стрелком по бегущей мишени равна 0,8. какова вероятность того, что этот стрелок промахнётся , сделав выстрел?
Решение: Пусть событие А - попадание по мишени, тогда Р(А)=0,8. Событие ![]() - промах.
- промах. ![]() = 1-Р(А)=1-0,8=0,2.
= 1-Р(А)=1-0,8=0,2.
Ответ: 0,2.
Задачи.
События
Невозможные, достоверные и случайные события
Для каждого из этих событий определить, каким оно является: невозможным, достоверным или случайным.
-
Из 26 учащихся класса двое справляют свой день рождения: 1) 25 января; 2) 31 июня.
Ответ: 1) случайное; 2) невозможное.
-
Случайным образом открывается художественное произведение и находится второе слово на левой странице. Это слово начинается: 1) с буквы М; 2) с буквы Ъ.
Ответ: 1) случайное; 2) невозможное.
-
Из списка журнала 9 класса (в котором есть и мальчики, и девочки) случайным образом выбран ученик: 1) это мальчик; 2) выбран ученик, которому 15 лет; 3) выбранному ученику 15 месяцев; 4) этому ученику больше двух лет.
Ответ: 1) случайное; 2) случайное; 3) невозможное.
-
Сегодня в Мариинске барометр показывает нормальное атмосферное давление. При этом: 1) вода в кастрюле закипит при температуре 70С; 2) когда температура упала до -3С, вода в луже замёрзла.
Ответ: 1) невозможное; 2) достоверное.
-
В нашей школе учатся 758 учеников. Событие А=в школе есть ученики с совпадающими днями рождения является случайным или достоверным. Выясните, произошло ли это событие в вашем классе?
Ответ: Событие А - достоверное, так как количество учащихся школы 758366 дней в году. Это событие случайное, так как количество учащихся нашего класса 26 человек.
-
Среди 150 билетов школьной благотворительной лотереи 30 выигрышных. Сколько билетов надо купить, чтобы событие А=вы ничего не выиграете было невозможным?
Ответ: 150-29=121 билет.
-
В 9 «Г» классе учится 16 мальчиков и 10 девочек. Какие из следующих событий являются невозможными, какие случайными, какие - достоверными:
А= в классе есть два человека, родившихся в разные месяцы;
В=в классе есть два человека, родившихся в одном месяце;
С=в классе есть два мальчика, родившихся в одном месяце;
D=в классе есть две девочки, родившиеся в одном месяце;
Е=все мальчики родились в разные месяцы;
F=все девочки родились в разные месяцы;
К=есть мальчик и девочка, родившиеся в одном месяце;
М= есть мальчик и девочка, родившиеся в разные месяцы.
Ответ: Событие А - случайное, событие В - достоверное, событие С - достоверное, событие D - случайное, событие Е - невозможное, событие F - случайное, событие K - случайное, событие M - случайное.
-
Около школы останавливаются автобусы трёх маршрутов, идущих в сторону лесозавода: № 5, № 13 и № 23. Интервал в движении автобусов каждого маршрута колеблется от 8 до 10 минут. Когда Саша, Маша, Кристина и Катя подошли к остановке, от неё отошёл автобус № 13, а ещё через 6 минут подошёл автобус № 5. После этого каждый из ребят высказал своё мнение о том, автобус какого маршрута будет следующим:
Саша: Следующим обязательно будет № 23.
Маша: Возможно, что следующим будет № 23.
Кристина: Возможно, что следующим будет № 13.
Катя: Невозможно, что следующим будет № 5.
С кем из ребят вы согласны, а с кем нет? Объясните сделанный выбор.
Ответ: Не прав только Саша.
9. На дорогу от дома до школы Миша тратит от 10 до 15 минут, если идёт пешком, и от 2 до 3 минут, если едет на автобусе. При каких интервалах движения автобусов событие А==по пути в школу Мишу обгонит хотя бы один автобус будет невозможным, при каких - случайным, при каких - достоверным?
Ответ: Больше 7 минут - случайным, меньше 7 минут - достоверным.
Совместные и несовместные события
-
В сыгранной Катей и Ларисой партии в шахматы: 1) Катя выиграла, Лариса проиграла; 2) Катя проиграла, Лариса проиграла.
Ответ: 1) совместные; 2) несовместные.
2. Из событий: 1) «идёт дождь»; 2) «на небе нет ни облака»; 3) «наступило лето» - составить всевозможные пары и выявить среди них пары совместных и пары несовместных событий.
Ответ: «идёт дождь» - «на небе нет ни облачка» - несовместные;
«наступило лето» - «на небе нет ни облачка» и «наступило лето» - «идёт
дождь» - совместные.
3. Из событий: 1) «наступило утро»; 2) «сегодня по расписанию 6 уроков»; 3) «сегодня 1 января»; 4) «температура воздуха в Мариинске +30С» - составить всевозможные пары и выявить среди них пары совместных и пары несовместных событий.
Ответ: «сегодня 1 января» - «температура воздуха в Мариинске +30С»; «сегодня по расписанию 6 уроков» - «температура воздуха в Мариинске +30С»; «сегодня 1 января» - «сегодня по расписанию 6 уроков» - несовместные; «наступило утро»- «сегодня 1 января»; «наступило утро» - «температура воздуха в Мариинске +30С»; «наступило утро» - «сегодня по расписанию 6 уроков» - совместные.
Противоположные события
1. Ниже перечислены разные события. Укажите противоположные им события.
а) Мою новую соседку по парте зовут или Таня, или Аня.
б) Из пяти выстрелов в цель попали хотя бы два.
в) На контрольной я не решил, как минимум, три задачи из пяти.
Решение: а) Мою новую соседку по парте зовут не Таня и не Аня.
б) Из пяти выстрелов в цель попали менее двух.
в) На контрольной я решил максимум две задачи из пяти.
2. Назовите событие, для которого противоположным является такое событие:
а) на контрольной работе больше половины класса получили пятёрки;
б) все семь пулек в тире у меня попали мимо цели;
в) в нашем классе все умные и красивые;
г) в кошельке у меня есть три рубля одной монетой, или три доллара одной бумажкой.
Решение: а) «На контрольной работе пятёрки получили не более половины класса», или «на контрольной работе больше половины класса не получили пятёрки». б) «В тире хотя бы одна пулька из семи у меня попала в цель». в) «В нашем классе есть хотя бы один не умный или не красивый». г) «В кошельке у меня нет ни трёх рублей одной монетой, ни трёх долларов одной бумажкой».
Сравнение шансов. Вероятностная шкала
1. Антон учится в 9 «Б» классе, Стас - в 9 «В», Игорь - в 9 «Г». От каждого класса по жребию выбирают одного делегата в школьный хор. Как вы думаете, у кого из друзей больше шансов петь в хоре, если в 9 «Б» учится 22 человека, в 9 «В» - 19 человек, а в 9 «Г» - 26 человек?
Решение: Определим шанс каждого из мальчиков: у Антона он будет равен ![]() , у Стаса -
, у Стаса - ![]() , у Игоря -
, у Игоря - ![]() . Так как из трёх дробей наибольшей будет
. Так как из трёх дробей наибольшей будет ![]() , то у Стаса шансов больше.
, то у Стаса шансов больше.
Ответ: У Стаса.
2. Когда Витя почувствовал себя нездоровым, мама, как обычно, поставила ему градусник. Расположите на вероятностной шкале следующие события:
А = Витина температура больше 36,6 ;
В = Витина температура равна 36,6 ;
С = Витина температура меньше 36,6 ;
D = Витина температура больше 20 ;
Е = Витина температура меньше 100 .
О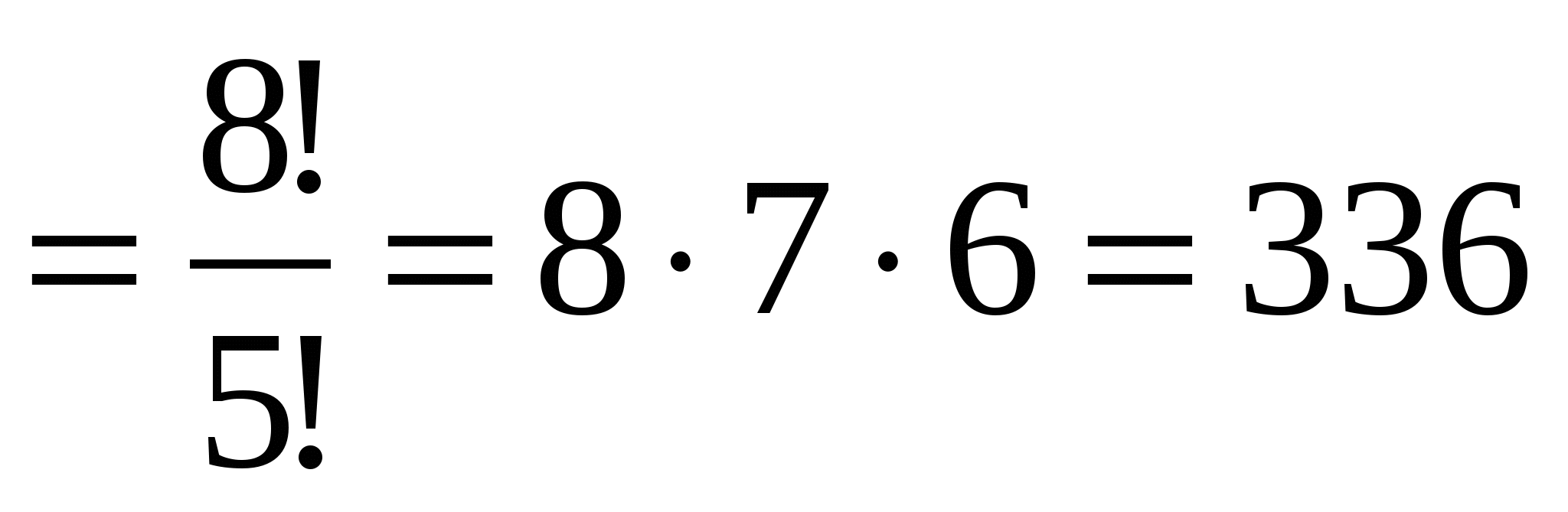
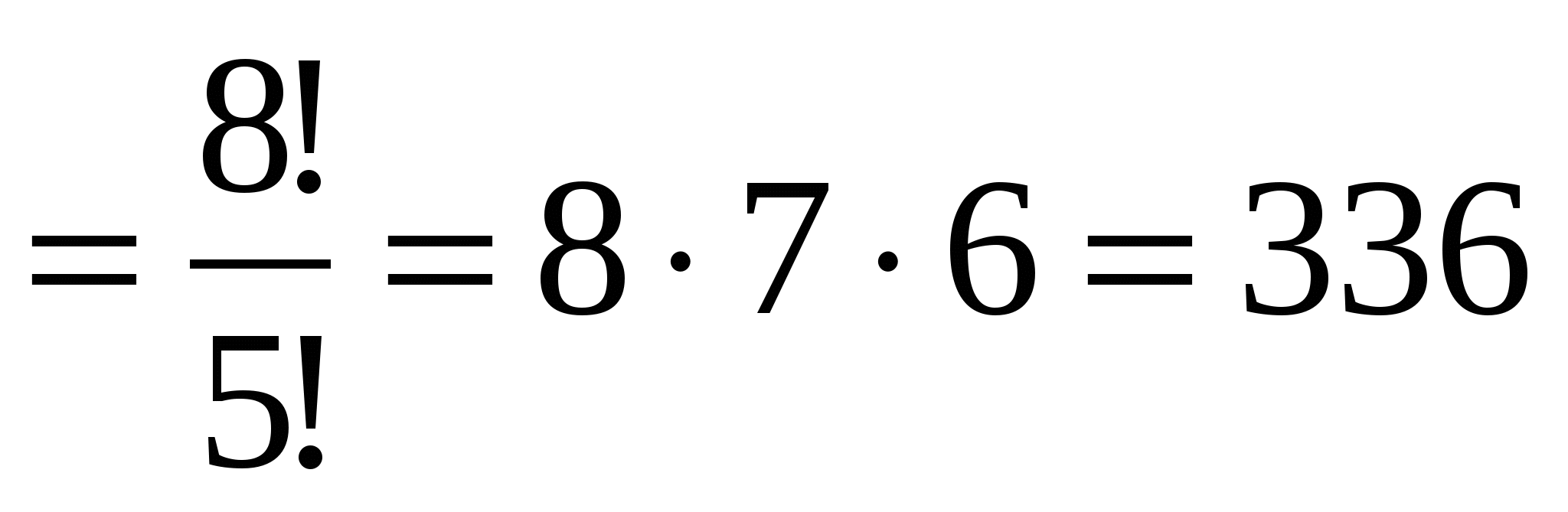 твет: В С А D
твет: В С А D
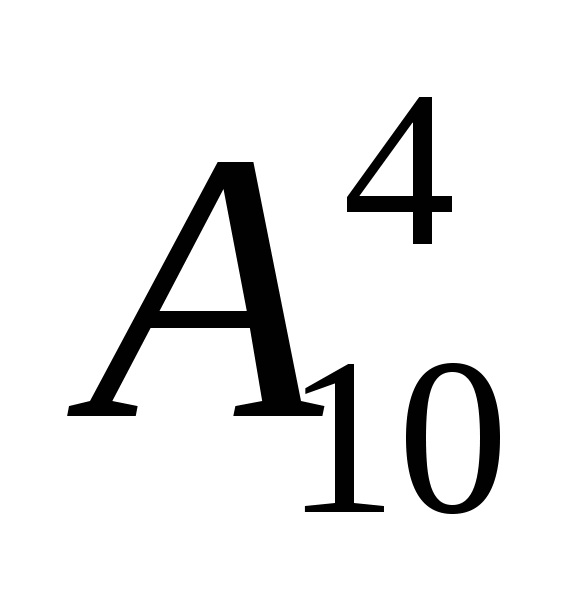 Е
Е
невозможные случайные достоверные
3. Пусть Х - время которое вы тратите на путь от дома до школы, а У - время на путь от школы до дома. Расположите на вероятностной шкале события:
А = Х 20 минут ;
В =Х 40 минут ;
С =У Х ;
D =У Х ;
Е =Х=У .
О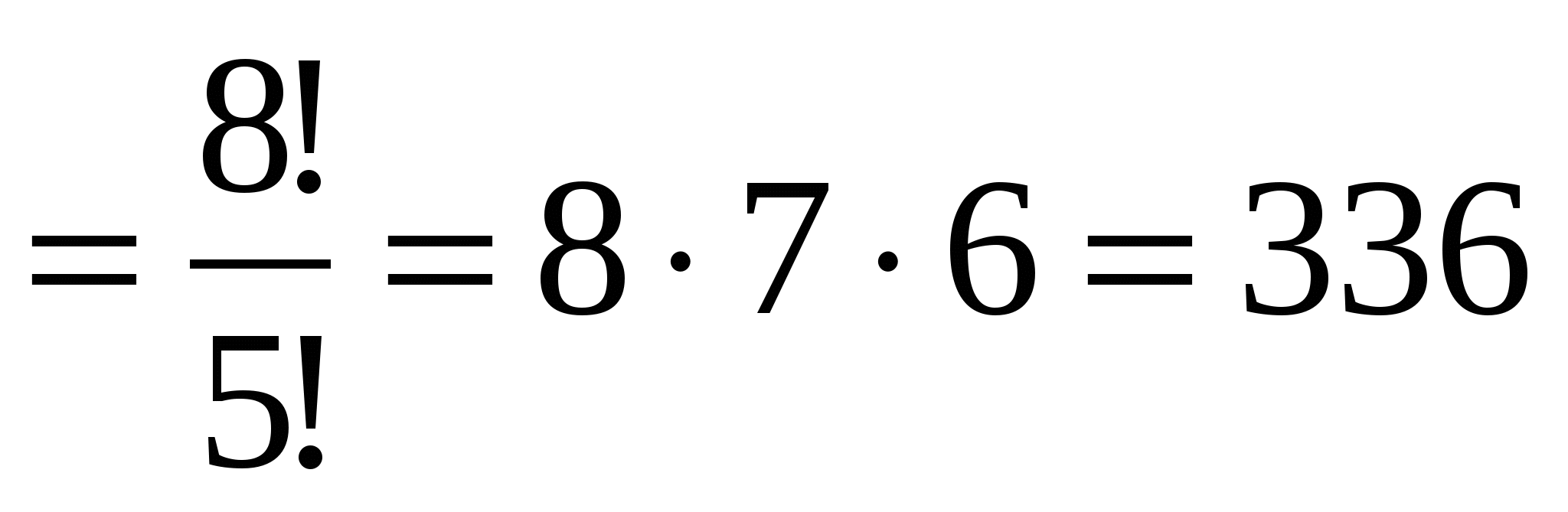
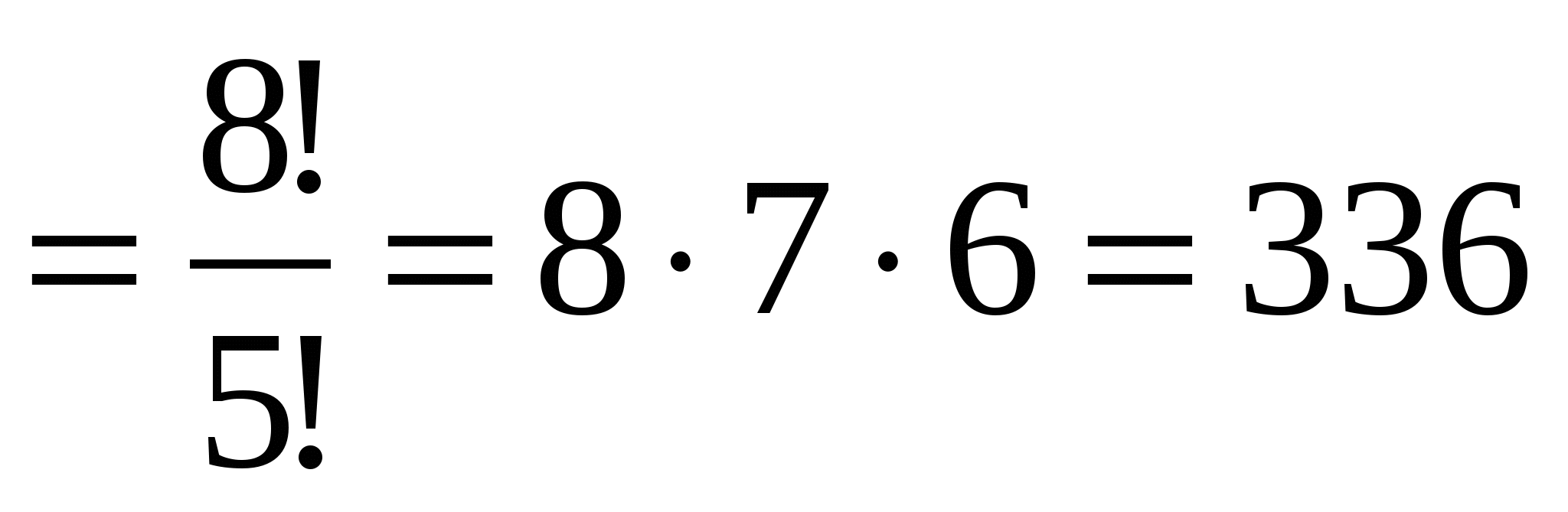 твет: Е А D С В
твет: Е А D С В
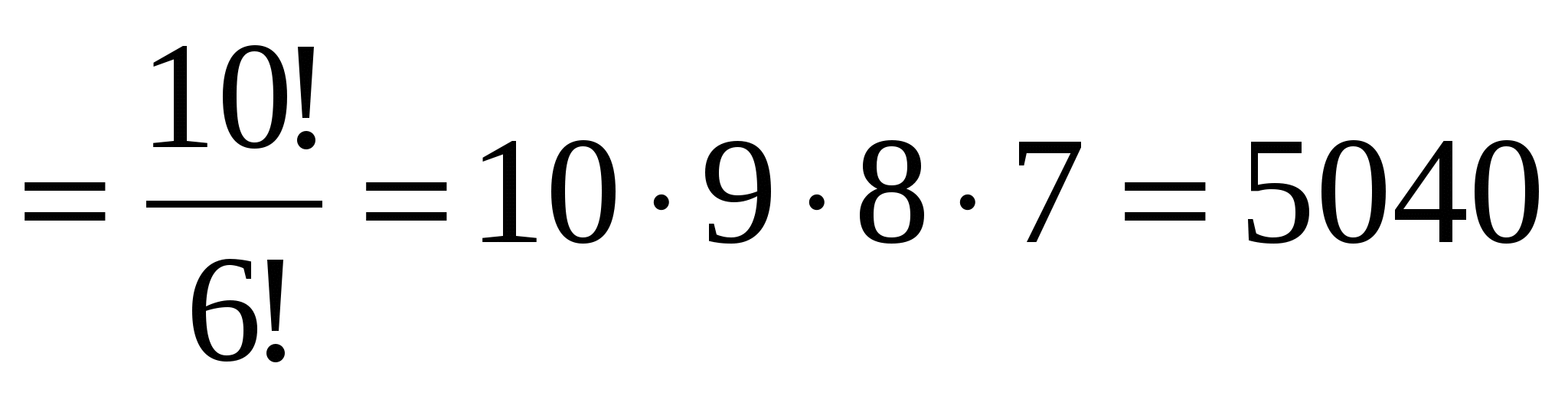
невозможное случайное достоверное
4. Решая предыдущую задачу, ученик получил расположение событий на вероятностной шкале, показанное на рисунке
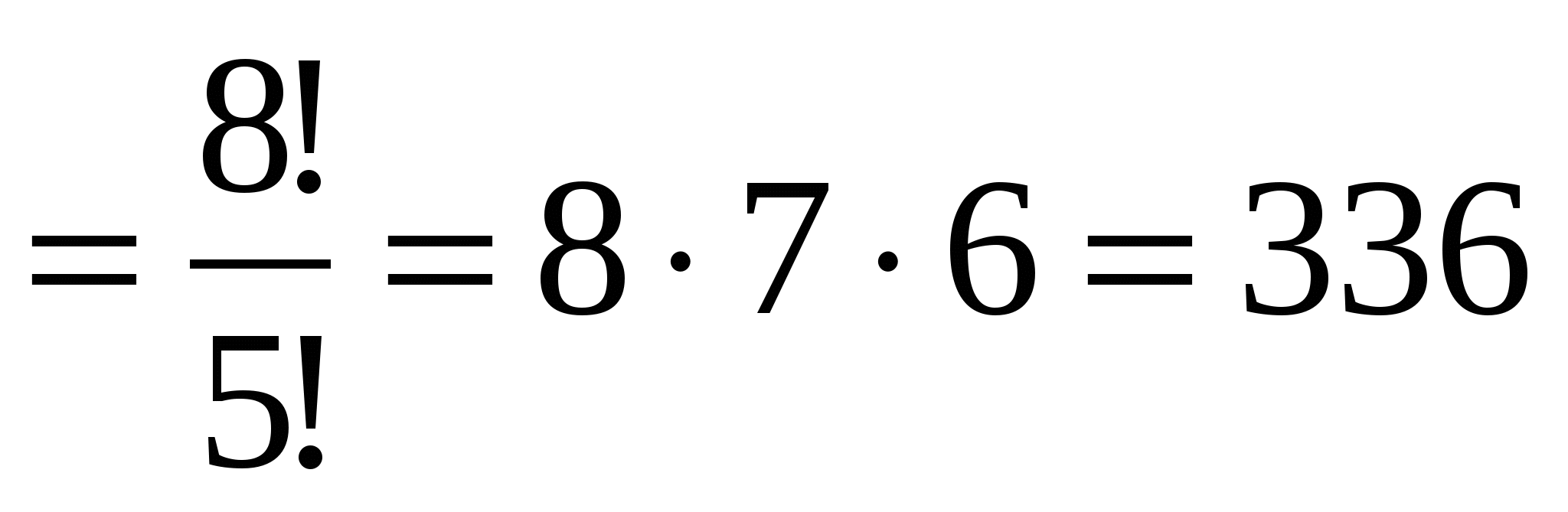
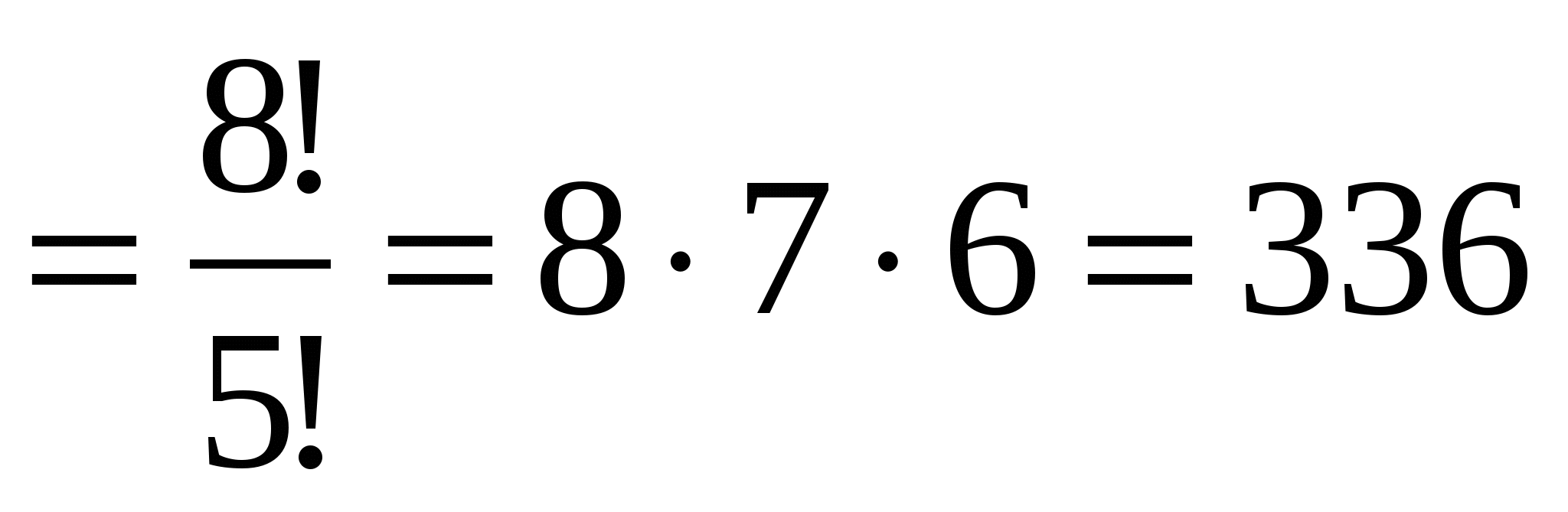 Е А D С В
Е А D С В

невозможное случайное достоверное
а) Куда ученик обычно добирается быстрее: в школу или из школы?
б) Известно, что в школу можно добраться одним из следующих
способов:
- пешком (около часа);
- на газели (около 15 минут);
- на автобусе (около 25 минут).
Каким из этих способов чаще всего пользуется ученик?
Ответ: а) быстрее добирается в школу; б) на автобусе.
5. В первой четверти отличник имел по русскому языку 5, а троечник - 3. Они пишут очередной диктант. Рассмотрите следующие события:
А = отличник сделает хотя бы одну ошибку;
В =троечник не сделает ни одной ошибке;
С = никто в классе не получит пятёрку;
D = отличник и троечник не сделают ошибки
Какие пары этих событий можно поставить вместо многоточий в утверждение: «Событие … более вероятно, чем событие ….»? Какие пары событий нельзя подставить в это утверждение и каких сведений для этого не хватает?
Ответ: А-С, В-D. Все остальные нельзя - для этого не хватает сведений о сложности диктанта.
6. В Димином классе 10 мальчиков и 9 девочек. Изобразите на рисунке, как соотносятся друг с другом следующие события:
А = все девочки родились в одном месяце;
В =есть две девочки, родившиеся в одном месяце;
С = один из Диминых друзей родился с ним в одном месяце;
D = есть два человека, родившихся в одном месяце
Можно ли придумать событие, которое «больше» события D? Почему?
Ответ:
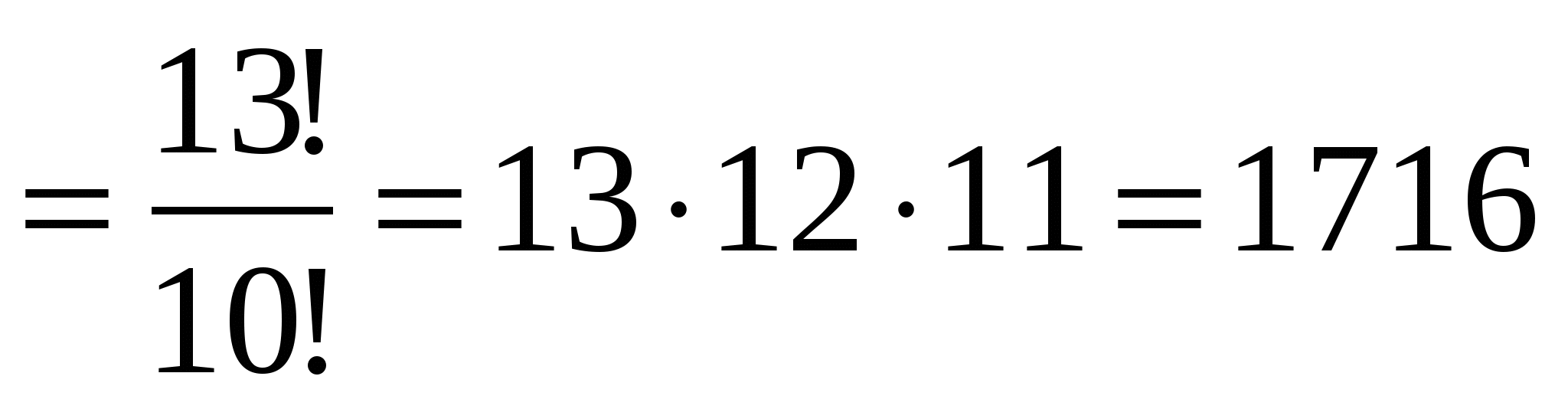
Вероятность
1. Таня забыла последнюю цифру номера телефона знакомой девочки и набрала её наугад. Какова вероятность того, что Таня попала к своей знакомой?
Решение: На последнем месте в номере телефона может стоять одна из 10 цифр 0, 1, 2, 3, 4, 5, 6, 7, 8, 9; n=10; все предыдущие цифры никакого значения не имеют. Из n=10 только одна цифра верная, поэтому m=1. вероятность события А, состоящего в том, что, набрав последнюю цифру номера наугад, Таня попала к своей знакомой, равна ![]() =
=![]() .
.
Ответ: ![]() .
.
2. Витя забыл две последние цифры номера телефона приятеля и набрал их наугад. С какой вероятностью этот звонок попадёт к приятелю?
Решение: Исходом в данном случае является пара десятичных цифр (0..9) с учётом порядка и с повторениями; общее число возможных исходов n=1010=100; все исходы считаем равновозможными. Среди этих исходов только один является правильным, соответствующим номеру телефона приятеля. Таким образом, событию А - «звонок попадёт к приятелю» благоприятствует только один исход mA=1; вероятность ![]() =
=![]() .
.
Ответ: 0,01.
3. Для новогодней лотереи отпечатали 1500 билетов, из которых 120 выигрышных. Какова вероятность того, что купленный билет окажется выигрышным?
Решение: Если продажа билетов будет организована так, что покупка любого из 1500 билетов будет равновозможна, то можно применить формулу классической вероятности. Пусть событие А - «купленный билет оказался выигрышным». Тогда количество благоприятствующих исходов m=120, а общее число равновозможных исходов n=1500; вероятность ![]()
![]()
![]()
Ответ: 0,08.
4. Для экзамена подготовили билеты с номерами от 1 до 25. какова вероятность того, что взятый наугад учеником билет имеет: 1) однозначный номер; 2) двузначный номер?
Решение: Общее число билетов n=25; извлечение каждого из них считается равновозможным. Рассмотрим событие А - «взятый билет имеет однозначный номер», В - «взятый билет имеет двузначный номер». Количество благоприятствующих исходов: mA=9 (одна цифра от 1 до 9); mB=16 (первая цифра 1 или 2, вторая цифра - от 0 до 9 после 1, от 0 до 5 после 2, всего 10+6=16). Искомые вероятности: ![]()
![]() ;
; ![]() =
=![]() .
.
Ответ: 1) ![]() ; 2)
; 2) ![]() .
.
5. Ученик при подготовке к экзамену не успел выучить один из тех 25 билетов, которые будут предложены на экзамене. Какова вероятность того, что ученику достанется на экзамене выученный билет?
Решение: Общее число билетов n=25; выбор каждого билета равновозможен. Событие А - «ученику достанется на экзамене выученный билет»; количество благоприятствующих исходов m=25-1=24. Вероятность события А: ![]() =
=![]() =0,96.
=0,96.
Ответ: ![]() .
.
6. В лотереи 1000 билетов, среди которых 20 выигрышных, приобретается один билет. Какова вероятность того, что этот билет: 1) выигрышный;
2) невыигрышный?
Решение: Общее число билетов n=1000; приобретение каждого из них равновозможно. Рассмотрим события и подсчитаем благоприятствующие им исходы: ![]() =
=![]() ,
, ![]() =
=![]() .
.
Ответ: 1) 0,02; 2) 0,98.
7. Женя купил 2 лотерейных билета, и один из них оказался выигрышным. Можно ли утверждать, что вероятность выигрыша в лотереи ![]() ?
?
Ответ: Нет. Одного испытания не достаточно, чтобы по частоте узнать вероятность.
8. Алёша забыл последнюю цифру телефонного номера и набрал её наугад,
помня только, что эта цифра нечётная. Найти вероятность того, что номер
набран правильно.
Решение: Исходом в данном случае являются цифры от 0 до 9, таких цифр -
10, но среди них нечётных только - 5. Отсюда следует, что M=5, N=10, значит
![]() =
=![]() .
.
Ответ: 0,5.
9. В классе 20 мальчиков и 10 девочек.
а) На класс дали один билет в цирк, который решено разыграть по жребию. Какова вероятность, что в цирк пойдёт мальчик?
б) Учитель истории знает, что 3 девочки и 5 мальчиков из класса были накануне в кино, поэтому не выучили домашнее задание. К сожалению, он не знает их фамилий, но очень хочет поставить кому-нибудь двойку. Кого ему лучше вызвать к доске - мальчика или девочку?
в) Влад не решил домашнюю задачу по математике. Какова вероятность, что учитель этого не узнает, если за урок он успевает спросить пятерых?
Решение: а) Общее число исходов равно 30. Благоприятных исходов - 20, значит ![]() =
= ![]()
![]() . б) Общее число исходов для девочек равно 10, для мальчиков - 20. Благоприятных исходов для девочек - 3, для мальчиков - 5, значит для девочек
. б) Общее число исходов для девочек равно 10, для мальчиков - 20. Благоприятных исходов для девочек - 3, для мальчиков - 5, значит для девочек ![]() =
=![]() , для мальчиков -
, для мальчиков -![]() . Так как
. Так как ![]() >
>![]() , поэтому лучше вызвать девочку. в) Общее число исходов равно 30. Благоприятных исходов - 25, значит
, поэтому лучше вызвать девочку. в) Общее число исходов равно 30. Благоприятных исходов - 25, значит ![]() =
=![]() =
=![]() .
.
Ответ: а) 0,067; б) лучше вызвать девочку; в) 0,833.
10. Для школьного новогоднего вечера напечатали 125 пронумерованных пригласительных билетов, между которыми предполагается разыграть главный приз. Какова вероятность, что номер счастливчика будет оканчиваться: а) на тройку; б) на девятку? в) Вова получил пригласительный билет с номером 33, а Таня - 99. Верно ли, что у Вовы больше шансов получить главный приз?
Решение: а) Общее число исходов равно 125. Благоприятных исходов - 13 (на тройку оканчиваются девять двузначных, три трёхзначных числа и само число -3), значит ![]() =
=![]() . б) Общее число исходов равно 125. Благоприятных исходов - 12 (на девятку оканчиваются девять двузначных, три трёхзначных числа и само число - 9), значит
. б) Общее число исходов равно 125. Благоприятных исходов - 12 (на девятку оканчиваются девять двузначных, три трёхзначных числа и само число - 9), значит ![]() =
=![]() . в) Общее число исходов равно 125. Благоприятных исходов и для Тани и для Вовы - 1, значит
. в) Общее число исходов равно 125. Благоприятных исходов и для Тани и для Вовы - 1, значит ![]() =
=![]() .
.
Ответ: а) 0,104; б) 0,096; в) Нет, не верно. У обоих шансы равны.
11. У Вики две одинаковые пары варежек. Уходя на улицу, она наугад берёт две варежки. Какова вероятность, что они окажутся парными (т.е. на разные руки)?
Ответ: ![]()
12. Вика потеряла одну из варежек на улице, и теперь их у неё три. Уходя на
улицу, она по-прежнему выбирает две варежки случайным образом. Какова вероятность того, что они окажутся парными?
Ответ: ![]() .
.
13. В лотереи участвуют 100 билетов. Разыгрывается один приз. а) Какова вероятность того, что вы ничего не выиграете на свой единственный билет?
б) Участвуя в той же лотереи, вы купили 20 билетов. Какова вероятность, что вы опять останетесь ни с чем?
Решение: а) Общее число исходов равно 100. Благоприятных исходов - 1, значит ![]() =
=![]() ; б) Общее число исходов равно 100. Благоприятных исходов - 80, значит
; б) Общее число исходов равно 100. Благоприятных исходов - 80, значит ![]() =
=![]() .
.
Ответ: а) 0,99; б) 0,8
14. Два друга живут в одном доме, а учатся в разных классах. Уроки в школе заканчиваются в интервале от 13 до 14 часов. После занятий они договариваются ждать друг друга на автобусной остановке в течение 20 минут. Сколько приблизительно раз за год им удаётся поехать домой вместе, если в году 200 учебных дней?
Решение: Вероятность поехать вместе будет ![]() . Следовательно, за год им удастся поехать вместе приблизительно
. Следовательно, за год им удастся поехать вместе приблизительно ![]() раз.
раз.
Ответ: 111 раз.
15. Расстояние от остановки «Горсад» до остановки «Школа» автобус проходит за 2 минуты, а Алёша - за 15 минут. Интервал движения автобусов - 25 минут. В случайный момент времени Алёша выходит из горсада, опаздывая в школу. Что ему лучше делать - идти пешком или подождать автобус?
Решение: Вероятность, что Алексей обгонит автобус, составит ![]() >
>![]() . Следовательно, лучше подождать автобус (хотя отклонение от
. Следовательно, лучше подождать автобус (хотя отклонение от ![]() столь незначительно, что можно пройтись и пешком).
столь незначительно, что можно пройтись и пешком).
Ответ: Лучше подождать автобус.
16. На школьном вечере среди присутствующих 160 учащихся случайным образом распространили 160 лотерейных билетов (каждый старшеклассник получил по одному билету). Среди этих билетов было 5 выигрышных. Какова вероятность того, что каждому старшекласснику из числа присутствующих достался: 1) выигрышный билет; 2) невыигрышный билет?
Решение: Каждому школьнику мог достаться любой из 160 билетов, т.е. n=160. 1) Благоприятствующих выигрышу билетов 5, т.е. m=5. Тогда ![]() =
=![]() . 2) Невыигрышных билетов 160-5=155, поэтому «не выигрышу» благоприятствует 155 исходов; m=155. Таким образом, вероятность получения невыигрышный билет равна
. 2) Невыигрышных билетов 160-5=155, поэтому «не выигрышу» благоприятствует 155 исходов; m=155. Таким образом, вероятность получения невыигрышный билет равна ![]() =
=![]() .
.
Ответ: 1) ![]() ; 2)
; 2) ![]() .
.
17. Для украшения ёлки принесли коробку, в которой находится 10 красных, 7 зелёных, 5 синих и 8 золотых шаров. Из коробки наугад вынимают один шар. Какова вероятность того, что он окажется: а) красным; б) золотым?
Решение: В коробке было всего 10+7+5+8=30 шаров, исход - изъятие одного шара определённого цвета. Рассмотрим события: а) А - «вынутый шар оказался красным»; mA=10; ![]() =
=![]() . б) В - «вынутый шар оказался золотым»; mB=8;
. б) В - «вынутый шар оказался золотым»; mB=8; ![]() =
=![]() .
.
Ответ: ![]() .
.
18. Тест содержит 25 вопросов. На каждый вопрос предлагаются два верных ответа, из которых нужно выбрать правильный. За сколько правильных ответов следует ставить положительную оценку?
Ответ: За 18 и более правильных ответов.
Комбинированные методы решения вероятностных задач
1. Набирая номер телефона, состоящий из 7 цифр, Антон забыл, в какой последовательности идут три последние цифры. Помня лишь, что это цифры 1, 5 и 9, он набрал первые 4 цифры, которые знал, и наугад комбинацию из цифр 1, 5 и 9. какова вероятность того, что Антон набрал верный номер?
Решение: Исходы - перестановки из трёх элементов (1, 5, 9); общее число исходов n=Р3=3!=6. Событие А - «Антон набрал верный номер»; mA=1 (есть только один правильный вариант расположения цифр 1, 5 и 9 в номере телефона); ![]() =
= ![]() .
.
Ответ: ![]() .
.
2. В пачке находятся одинаковые по размеру 7 тетрадей в линейку и 5 в клетку. Из пачки наугад берут 3 тетради. Какова вероятность того, что все 3 тетради окажутся в клетку?
Решение: Исходы - все возможные наборы по 3 тетради из 12, находящихся в пачке, без учёта порядка их расположения в наборе (сочетания); общее количество возможных исходов ![]() . Событие А - «все тетради в наборе - в клетку»;
. Событие А - «все тетради в наборе - в клетку»; ![]() (выбор трёх из пяти тетрадей в клетку) =
(выбор трёх из пяти тетрадей в клетку) = ![]() . Вероятность
. Вероятность ![]() =
=![]() .
.
Ответ: ![]() .
.
3. Четыре билета на ёлку распределили по жребию между 15 мальчиками и 12 девочками. Какова вероятность того, что билеты достанутся 2 мальчикам и 2 девочкам?
Решение: Исходы - все возможные группы из 4 человек - обладателей билетов на ёлку, составленные из 27 желающих. Порядок выбора значения не имеет (каждый из четверых получает одинаковый билет). Общее число возможных исходов ![]() . Событие А - «билеты достанутся 2 мальчикам и 2 девочкам»
. Событие А - «билеты достанутся 2 мальчикам и 2 девочкам» ![]() (выбор двух мальчиков)
(выбор двух мальчиков) ![]() (выбор двух девочек)
(выбор двух девочек) ![]() . Искомая вероятность
. Искомая вероятность ![]()
![]() .
.
Ответ: ![]() .
.
4. На полке 12 книг, из которых 4 - это учебники. С полки наугад снимают 6 книг. Какова вероятность того, что 3 из них окажутся учебниками?
Решение: Исходы - все возможные наборы из 6 книг без учёта порядка, снимаемых с полки; общее число исходов ![]() . Событие А - «из 6 снятых книг 3 оказались учебниками»;
. Событие А - «из 6 снятых книг 3 оказались учебниками»; ![]() (выбор 3 учебников из 4 имеющихся)
(выбор 3 учебников из 4 имеющихся) ![]() (дополнение набора 3 книгами из 8 книг - не учебников)
(дополнение набора 3 книгами из 8 книг - не учебников) ![]() . Искомая вероятность
. Искомая вероятность ![]() =
= ![]() .
.
Ответ: ![]() .
.
5. В тёмном ящике 5 выигрышных билетов и 4 проигрышных. Вы случайно вытаскиваете 3 билета. Найдите вероятность того, что: а) все билеты выигрышные; б) есть ровно один проигрышный билет; в) есть ровно два выигрышных билета; г) есть хотя бы один выигрышный билет.
Решение: В ящике всего 9 билетов. Исходы - все возможные наборы по 3 билета без учёта порядка их расположения в наборе; общее число исходов ![]() . Рассмотрим события: а) А - «все три извлечённых билета - выигрышные»;
. Рассмотрим события: а) А - «все три извлечённых билета - выигрышные»; ![]() . Вероятность
. Вероятность ![]() =
=![]() =
=![]() . б) В - «среди трёх извлеченных билетов ровно один проигрышный»;
. б) В - «среди трёх извлеченных билетов ровно один проигрышный»; ![]() (к одному из 4 проигрышных выбираем ещё два выигрышных билета)
(к одному из 4 проигрышных выбираем ещё два выигрышных билета) ![]() ;
; ![]() =
=![]() . в) С - «среди трёх извлечённых билетов есть ровно два выигрышных»;
. в) С - «среди трёх извлечённых билетов есть ровно два выигрышных»; ![]() (выбор двух выигрышных)
(выбор двух выигрышных) ![]() ;
; ![]() =
=![]() . г) D - «среди трёх извлечённых билетов есть хотя бы один выигрышный»;
. г) D - «среди трёх извлечённых билетов есть хотя бы один выигрышный»; ![]() (выбор всех трёх проигрышных) = 84-4=80; благоприятствующие исходы мы нашли, отняв от числа всех исходов «ненужные» исходы. Вероятность
(выбор всех трёх проигрышных) = 84-4=80; благоприятствующие исходы мы нашли, отняв от числа всех исходов «ненужные» исходы. Вероятность ![]() .
.
Ответ: а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
6. Экзамен по истории включает 60 вопросов. Валера утверждает, что подготовил 80% всех вопросов экзамена. Папа задал ему три вопроса, ни на один из которых он не ответил. Есть ли у папы основания подозревать сына во лжи?
Ответ: Да, есть. Произошло событие, вероятность которого равна ![]() - очень маловероятное.
- очень маловероятное.
Вероятность противоположного события
1. В школьном научном обществе 10 человек: 7 мальчиков и 3 девочки. Случайным образом из членов этого общества выбирают двух учащихся на городскую конференцию. Какова вероятность того, что среди выбранных двух человек окажется хотя бы одна девочка?
Решение: Пусть событие А - среди выбранных двух человек окажется хотя бы одна девочка (т.е. либо одна, либо две девочки). Тогда событие ![]() - среди выбранных двух человек нет ни одной девочки (т.е. выбраны только мальчики). Найдём сначала вероятность события
- среди выбранных двух человек нет ни одной девочки (т.е. выбраны только мальчики). Найдём сначала вероятность события ![]() . Благоприятствующими событию
. Благоприятствующими событию ![]() исходами будут всевозможные пары, составленные из 7 мальчиков. Их число равно (7-1)7:2=21, т.е. m = 21. Число возможных пар, составленных из 10
исходами будут всевозможные пары, составленные из 7 мальчиков. Их число равно (7-1)7:2=21, т.е. m = 21. Число возможных пар, составленных из 10
школьников равно (10-1)10:2=45, т.е. n =45. Таким образом, ![]() . Тогда
. Тогда ![]() .
.
Ответ: ![]() .
.
2. Вероятность выигрыша, приходящаяся на один билет в школьной лотереи, равна: 1) 0,03; 2) ![]() . Какова вероятность получения невыигрышного билета в этой лотереи?
. Какова вероятность получения невыигрышного билета в этой лотереи?
Решение: Событие «получен выигрышный билет» и «получен невыигрышный билет» - противоположные, поэтому искомые вероятности находим по теореме о вероятности противоположного события. 1) Р(А)=0,03; ![]() =1- 0,03=0,97. 2) Р(А) =
=1- 0,03=0,97. 2) Р(А) =![]() ;
; ![]() =
=![]() .
.
Ответ: ![]() .
.
3. Вероятность попадания Андреем по мишени из винтовки равна 0,7. Какова вероятность того, что Андрей промахнётся, сделав выстрел7
Решение: Пусть событие А - попадание по мишени. Тогда Р(А)=0,7. Событие ![]() - промах. Согласно формуле
- промах. Согласно формуле ![]() =1- 0,7=0,3.
=1- 0,7=0,3.
Ответ: 0,3.
Относительная частота
На практике - при изучении случайных явлений в естествознании, экономике, медицине, производстве - часто встречаются испытания, у которых число возможных исходов необозримо велико. А в ряде случаев до проведения реальных испытаний трудно или невозможно установить равновозможность исходов испытания. Поэтому, наряду с классическим, на практике используют так называемое статистическое определением вероятности. Чтобы выяснить, насколько вероятно то или иное случайное событие, связанное с экспериментом, нужно подсчитать, как часто оно происходит. Для этого используют две важные величины:
Относительной частотой события А в данной серии испытаний называют отношение числа испытаний М, в которых это событие произошло, к числу всех проведённых испытаний N, при этом число М называют абсолютной частотой или частотой события А.
Абсолютная частота показывает, сколько раз в серии экспериментов наблюдалось данное событие; относительная частота показывает, какая доля экспериментов завершилась наступлением данного события.
Относительную частоту события А обозначают ![]() , поэтому по определению:
, поэтому по определению: ![]() .
.
Пример. Во время тренировки в стрельбе по цели было сделано 30
выстрелов и зарегистрировано 26 попаданий. Какова относительная частота
попадания по цели в данной серии выстрелов?
Решение: Событие А - попадание по цели произошло в 26 случаях, т.е. М=26. Общее число испытаний N=30, поэтому ![]() =
=![]() .
.
Ответ: ![]() .
.
Под статистической вероятностью понимают число, около которого колеблется относительная частота события при большом числе испытаний.
Таблицы распределения случайной величины
Случайной называется величина, которая в результате опыта может принять то или иное возможное значение, неизвестное заранее, но обязательно одно.
Пример. Случайная величина Х - оценка за контрольную работу учащихся 9 класса, может принимать значения Х1=1, Х2=2, Х3=3, Х4=4, Х5=5. Распределение величины Х по частотам (или относительным частотам) можно записать лишь после реального подсчёта каждого её значения.
Задача. После проверки контрольной работы в 9 классе учитель сделал подсчёт каждой из полученных оценок и составил таблицу распределения значений величины Х (оценка учащегося) по частотам М.
Х
1
2
3
4
5
Подсчёт случаев
М
1
3
15
9
3
Составить таблицу распределения значений величины Х по относительным частотам.
Решение: Число учащихся 9 класса N, писавших контрольную работу, равно сумме частот (М) всех выставленных оценок, т.е. N=1+3+15+9+3=31. Зная, что относительные частоты находятся по формуле ![]() , вычислим относительную частоту для каждого значения величины Х:
, вычислим относительную частоту для каждого значения величины Х: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Х
1
2
3
4
5
W
![]()
![]()
![]()
![]()
![]() Ответ:
Ответ:
Относительные частоты
1. Дано распределение дней рождения старшеклассников (учащихся 9-11 классов) по месяцам и дням недели
-
пн
вт
ср
чт
пт
сб
вс
январь
0
1
3
4
0
0
1
февраль
2
4
1
2
3
0
2
март
2
2
0
2
4
2
0
апрель
3
2
5
8
0
3
2
май
4
0
2
1
1
1
2
июнь
4
2
2
1
3
2
0
июль
0
1
4
2
1
2
0
август
1
2
4
4
2
0
1
сентябрь
0
1
2
1
2
3
5
октябрь
1
2
0
0
2
1
0
ноябрь
0
2
4
1
1
5
1
декабрь
2
2
3
2
0
2
2
Найдите относительные частоты событий:
А = старшеклассник родился в майское воскресенье;
В =старшеклассник родился в зимний четверг;
С = старшеклассник родился в понедельник;
D = старшеклассник родился весной
Решение: Всего в мае родилось 11 учащихся, из них только двое родились в воскресенье, значит, вероятность события А равна ![]() =
=![]() . Всего в зимние месяцы родилось 14+9+14=37 старшеклассников, из них 2+4+2=8 родились в четверг, значит, вероятность события В равна
. Всего в зимние месяцы родилось 14+9+14=37 старшеклассников, из них 2+4+2=8 родились в четверг, значит, вероятность события В равна ![]() =
=![]() . В понедельник родились 2+2+3+4+4+1+1+2=19 старшеклассников из 154, значит, вероятность события С равна
. В понедельник родились 2+2+3+4+4+1+1+2=19 старшеклассников из 154, значит, вероятность события С равна ![]() =
=![]() . Весной родились 12+23+11=46 старшеклассников из 154, значит, вероятность события D равна
. Весной родились 12+23+11=46 старшеклассников из 154, значит, вероятность события D равна ![]() =
=![]() .
.
Ответ: ![]() ;
;![]() ;
;![]() ;
;![]() .
.
-
Рост каждого из 50 девятиклассников занесли в таблицу:
165
170
165
165
175
160
170
170
172
170
178
170
178
174
165
165
175
175
172
160
175
172
160
170
170
178
176
176
175
172
170
170
172
170
178
176
180
174
176
181
180
170
170
174
180
175
175
174
174
172
По имеющимся данным составить таблицу распределения значений случайной величины Х - роста девятиклассниц: а) по частотам (М); б) по относительным частотам (W).
Решение: Величина Х принимает значения Х1=160, Х2=165, Х3=170, Х4=172, Х5=174, Х6=175, Х7=176, Х8=178, Х9=180, Х10=181. Подсчитывая число (М) девятиклассников каждого роста, заносим данные в частотную таблицу, затем для каждого значения Х находим значение относительной частоты W, зная, что N=50.
Х
160
165
170
172
174
175
176
178
180
181
М
3
5
12
6
5
7
4
4
3
1
W
0,06
0,1
0,24
0,12
0,1
0,14
0,08
0,08
0,06
0,02
3. В таблице записаны размеры обуви 20 девочек 9-х классов:
38
38
39
38
41
39
37
38
37
35
38
37
36
37
38
38
39
38
38
38
На основании этих данных составить таблицы распределения по частотам (М) и относительным частотам (W) значений случайной величины Х - размеров обуви девочек 9-х классов.
Решение: Величина Х принимает значения Х1=35, Х2=36, Х3=37. Х4=38, Х5=39, Х6=41. Подсчитывая число (М) девятиклассниц каждого размера обуви, заносим данные в частотную таблицу, затем для каждого значения Х находим значение относительной частоты W, зная, что N=20.
Х
35
36
37
38
39
41
М
1
1
4
10
3
1
W
0,05
0,05
0,2
0,5
0,15
0,05
4. В таблице приведены размеры одежды 50 учащихся 9-х классов:
36
46
36
36
38
40
42
42
46
36
44
36
42
44
42
42
42
44
44
42
42
40
36
38
38
44
46
36
40
44
40
38
38
38
50
46
44
42
42
48
40
44
42
42
46
40
44
38
38
36
На основании этих данных составить таблицы распределения по частотам и относительным частотам значений случайной величины Х - размеров одежды учащихся 9-х классов.
Решение: Величина Х принимает значения Х1=36, Х2=38, Х3=40. Х4=42, Х5=44, Х6=46, Х7=48, Х8=50. Подсчитывая число (М) девятиклассников каждого размера одежды, заносим данные в частотную таблицу, затем для каждого значения Х находим значение относительной частоты W, зная, что N=50.
Х
36
38
40
42
44
46
48
50
М
8
8
6
12
9
5
1
1
W
0,16
0,16
0,12
0,24
0,18
0,1
0,02
0,02
5. Время, затраченное на путь от дома до школы, каждого из 50 девятиклассников занесли в таблицу:
15
15
30
5
5
15
5
3
15
20
20
20
20
30
20
10
25
10
30
10
25
10
20
25
30
10
10
45
15
35
15
15
20
20
16
25
25
3
5
25
25
5
25
15
10
25
15
25
15
15
На основании этих данных составить таблицы распределения по частотам и относительным частотам значений случайной величины Х - время, затраченное на путь от дома до школы учащимися 9-х классов.
Решение: Величина Х принимает значения Х1=3, Х2=5, Х3=10. Х4=15, Х5=16, Х6=20, Х7=25, Х8=30, Х9=35, Х10=45. Подсчитывая число (М), заносим данные в частотную таблицу, затем для каждого значения Х находим значение относительной частоты W, зная, что N=50.
Х
3
5
10
15
16
20
25
30
35
45
М
2
5
7
11
1
8
10
4
1
1
W
0,04
0,1
0,14
0,22
0,02
0,16
0,2
0,08
0,02
0,02