- Учителю
- Учебно-исследовательский проект по теме: 'Изучение диаграммных методов и их применение в решении арифметических задач'
Учебно-исследовательский проект по теме: 'Изучение диаграммных методов и их применение в решении арифметических задач'









































































































Учебно-исследовательский проект по теме: «Изучение диаграммных методов и их применение при решении арифметических задач»
СОДЕРЖАНИЕ
-
ВВЕДЕНИЕ
3
ОСНОВНАЯ ЧАСТЬ
1 Понятия и принципы построения одномерных и двумерных диаграмм. Вспомогательная теорема и вспомогательные построения
5
2 Одномерные и двумерные диаграммы в решении арифметических задач
10
2.1 Применение одномерных (линейных) диаграмм в решении арифметических задач
10
2.2 Применение двумерных диаграмм в решении арифметических задач
14
ЗАКЛЮЧЕНИЕ
18
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
19
ВВЕДЕНИЕ
С арифметики, науке о числах, начинается наше знакомство с математикой. Наука арифметика изучает действия над числами, различные правила обращения с ними, учит решать задачи, сводящиеся к сложению, вычитанию, умножению и делению чисел.
Арифметика и геометрия - давние спутники человека. В истории математики процесс слияния арифметики и геометрии происходил на протяжении многих веков. Можно отчетливо проследить «геометризацию» арифметики: сложные правила и закономерности, выраженные формулами, становятся понятнее, если удается изобразить их геометрически.
На олимпиадах и конкурсах часто встречаются арифметические задачи, решения которых алгебраическим методом требует довольно громоздких вычислений. Поэтому у меня возник вопрос: «Существуют ли другие методы решения таких задач?» Познакомившись с книгами Александрова И. И. и Александровой А. И. «Методы решения арифметических задач» [1], А. И. Островского и Б. А. Кордемского «Геометрия помогает арифметике» [4], я остановила свой выбор на изучении решении арифметических задач с помощью построения диаграмм.
В нашей работе рассмотрено применение некоторых геометрических приемов, а именно одномерных и двумерных диаграмм, к решению разнообразных арифметических задач. Решение задач осуществляется при помощи чертежей-диаграмм. Построение этих диаграмм дает возможность «увидеть» задачу - установить и исследовать связи, существующие между величинами, входящими в задачу, выбрать кратчайший путь решения.
Цель исследования - показать возможность применения одномерных и двумерных диаграмм как альтернативного решения арифметических задач.
Для достижения поставленной цели были сформулированы следующие задачи:
-
изучить литературу по теме исследования;
-
научиться строить одномерные (линейные) и двумерные диаграммы, изображая подходящими геометрическими фигурами численные значения величин, входящих в условие задачи;
-
подобрать арифметические задачи, в решении которых возможно применение диаграмм;
-
провести сравнительный анализ решений арифметических задач.
Объектом исследования являются арифметические задачи.
Предметом исследования является диаграммный метод решения арифметических задач
Методы исследования:изучение литературы по теме исследования, геометрические построения, сравнительный анализ.
Актуальность исследования заключается в том, что умение пользоваться диаграммным методом имеет важное значение в практической деятельности, так как постоянно мы сталкиваемся с различными задачами, решение которых этим методом позволяет нам получить быстрые, наглядные и осмысленные решения.Диаграммные методы нужны для приобретения практических навыков применений геометрических знаний, и потому представляют познавательный интерес.
Нами была выдвинута гипотеза, что арифметические задачи, рассматриваемые в данной работе, можно решить с помощью построения одномерной или двумерной диаграмм, не проводя громоздких вычислений.
1 Понятия и принципы построения одномерных и двумерных диаграмм. Вспомогательная теорема и вспомогательные построения
Диаграмма - это чертеж или рисунок, на котором условно изображены в виде отдельных фигур различные значения одной и той же величины или нескольких сравнимых величин [1].
Простейшим геометрическим изображением величины и ее частей, входящих в условие задачи, является так называемая одномерная (или линейная) диаграмма. Одномерная диаграмма - это обычно отрезок или несколько отрезков, длины которых соответствуют численным значениям рассматриваемой величины (отрезки могут быть заменены прямоугольниками одинаковой ширины) [4].
Очень часто рассматриваемая величина является произведением двух других величин. Например, вес груза равен произведению количества ящиков на вес одного ящика; стоимость покупки равна произведению количества купленных килограммов на цену одного килограмма; путь, пройденный при равномерном движении, равен произведению скорости на время и т.д.
С другой стороны, известно, что площадь прямоугольника равна произведению двух его сторон.
Поэтому, в тех задачах, где одна из рассматриваемых величин является произведением двух других, целесообразно для наглядности представлять такое произведение в виде площади прямоугольника или параллелограмма, или треугольника, то есть в виде двумерной диаграммы.
Применение двумерных диаграмм в качестве моделей решения арифметических задач требует выполнения геометрических построений несколько более сложных, чем в случае применения линейных диаграмм. Для этого нам понадобилась вспомогательная теорема.
Теорема 1 (рисунок 1).
Если через произвольную точку Е диагонали АС прямоугольника АВСD проведены попарно параллельные прямые FG и АВ и HJ и AD, то
1) образовавшиеся при этом прямоугольники HBGEиFEJD (желтые) равновелики;
2) прямоугольники ABGF (синий) и AHJD (красный) равновелики;
3) отрезки FH,DB,JG параллельны.
Доказательство.
D J C
F E G
A H B
Рисунок 1
1) Диагональ АС делит каждый из трех прямоугольников АВСD, AHEFи EGCJ на два равных треугольника, т.е. 
Вычитая из первого равенства второе, а затем третье, получим, что 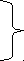
2) Дополним каждый из двух равновеликих прямоугольников HBGEи FEJD прямоугольником AHEF. Полученные таким способом два прямоугольника ABGFи AHJD также будут равновеликими. Следовательно, 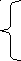
3) FG || DB || JG как секущие при соответствующих параллельных прямых.
Теорема доказана.
Выполним теперь несколько построений, основываясь на доказанной теореме [4].
Построение 1.
Преобразовать данный прямоугольник ABGF (синий) в равновеликий прямоугольник (зеленый) с заданным основанием AH, лежащим на стороне АВ, причем AH AB (рисунок 2).
AB (рисунок 2).
F G
A H B
Рисунок 2
Первый способ (рисунок 3). Проведем прямую  , перпендикулярно сторонеAH; она пересечет сторону FGв точке Е. Проведем прямую АЕ до пересечения с продолжением BGв точке С. Точка С определяет высоту ВС искомого прямоугольника (зеленого) с основанием АH. Действительно, достраивая полученную фигуру до прямоугольника ABCD, получаем, на основании вспомогательной теоремы, что зеленый прямоугольник А
, перпендикулярно сторонеAH; она пересечет сторону FGв точке Е. Проведем прямую АЕ до пересечения с продолжением BGв точке С. Точка С определяет высоту ВС искомого прямоугольника (зеленого) с основанием АH. Действительно, достраивая полученную фигуру до прямоугольника ABCD, получаем, на основании вспомогательной теоремы, что зеленый прямоугольник А D с заданным основанием AH равновелик синему прямоугольнику ABGF.
D с заданным основанием AH равновелик синему прямоугольнику ABGF.
D 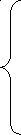 C
C
F E G
A H B
Рисунок 3
Второй способ (рисунок 4). Проведем прямую  перпендикулярно стороне AH и прямолинейный отрезок HF. Из точки G проведем прямую
перпендикулярно стороне AH и прямолинейный отрезок HF. Из точки G проведем прямую , параллельную HF, до пересечения с прямой
, параллельную HF, до пересечения с прямой  в точке J. Точка J определяет высоту HJ искомого прямоугольника AHJD. Чтобы в этом убедиться, достроим полученную фигуру до прямоугольника ABCD и проведем прямолинейные отрезки АЕ и ЕС (штриховые). Образуются равные пары углов:
в точке J. Точка J определяет высоту HJ искомого прямоугольника AHJD. Чтобы в этом убедиться, достроим полученную фигуру до прямоугольника ABCD и проведем прямолинейные отрезки АЕ и ЕС (штриховые). Образуются равные пары углов:  . Но так как
. Но так как  вследствие параллельности HF и GJ, то
вследствие параллельности HF и GJ, то  . Следовательно, АС - прямолинейный отрезок - диагональ прямоугольника ABCD. На основании вспомогательной теоремы заключаем, что прямоугольники ABGFи AHJD равновелики.
. Следовательно, АС - прямолинейный отрезок - диагональ прямоугольника ABCD. На основании вспомогательной теоремы заключаем, что прямоугольники ABGFи AHJD равновелики.
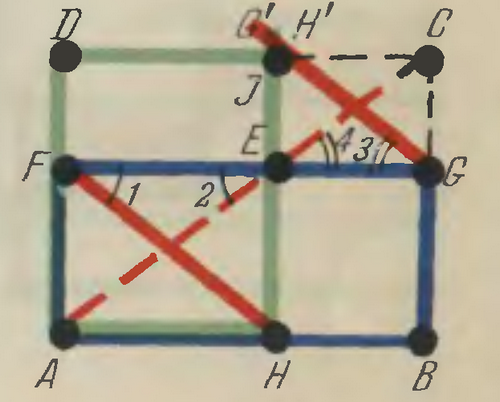
Рисунок 4
Построение 2. Преобразовать данную фигуру AEFGCD (зеленую), составленную из двух смежных прямоугольников ABCD и BEFG (рисунок 5) в равновеликий прямоугольник с основанием АЕ (синий). Применим способы построения, аналогичные предыдущим.
GD C
F
A В Е
Рисунок 5
Первый способ (рисунок 6). Продолжим FG до пересечения со стороной AD в точке H. Построим прямоугольник HFGDи проведем диагональ HJ. Точка К пересечения HJ и ВС определяет высоту ВК искомого прямоугольника AELM с заданным основанием АЕ.В самом деле, на основании вспомогательной теоремы, желтые прямоугольники равновелики, следовательно, прямоугольник AELM равновелик первоначально данной фигуре AEFGCD.
D C J
M K L
H G F
A B E
Рисунок 6
Второй способ (рисунок 7). Построим прямолинейный отрезок FD и из точки G проведем прямуюGM || FD до пересечения с AD в точке М, АМ - высота искомого прямоугольника AELM.Для доказательства продолжимFG до точки H; тогда будем иметь: .
.
Это значит, что прямоугольники MKCD и GFLK равновелики и, следовательно, прямоугольник AELM равновелик первоначально данной фигуре AEFGCD.
D C
M K L
H G F
A E
Рисунок 7
Построение третье (обратное предыдущему). Преобразовать прямоугольник AELM в два смежных прямоугольника, в сумме равновеликих данному прямоугольнику AELM, причем заданы высоты ADи EF искомых прямоугольников, а сумма их оснований должна равняться основанию АЕ данного прямоугольника (рисунок 8).
D
M L
F
A E
Рисунок 8
Решение.
Для решения задачи можно применить любой из предыдущих способов построения. Достаточно, например, на AD отложить AH = EF(рисунок 9), а на продолжении EFотложитьEJ = AD и провести прямуюHJ. Точка К пересечения HJ и ML определяет размеры MK и KLоснований искомых прямоугольников ABCD и BEFG. Равновеликость получившейся фигуры AEFGCD прямоугольнику AELM доказывается так же, как и в предыдущей задаче.
D C J
M K L
H G F
A B E
Рисунок 9
2 Одномерные и двумерные диаграммы в решении арифметических задач
2.1 Применение одномерных (линейных) диаграмм в решении арифметических задач
Рассмотрим несколько арифметических задач, в решении которых применим линейные диаграммы.
Задача 2.1.1
Мальчика спросили, сколько у него братьев и сестер. Он ответил: «Столько же братьев, сколько и сестер». Тогда спросили сестру, сколько у нее братьев и сестер. Она ответила: «У меня сестер меньше, чем братьев». Сколько было братьев и сколько было сестер? (Мальчик и девочка, отвечая на вопросы, не считают себя).
Решение.
Построим диаграммы. Число мальчиков будем изображать синими отрезками, а девочек - красными.
Мальчик сказал: «У меня столько же братьев, сколько и сестер». Условно изобразим равными отрезками слева - всех его братьев, справа - всех его сестер (рисунок 10). При этом отрезок «мои сестры» (сестры мальчика) изображает неизвестное число девочек.
Девочка сказала: «У меня сестер вдвое меньше, чем братьев». Условно изобразим отрезками слева - всех ее братьев, справа - всех ее сестер (рисунок 10). На этой диаграмме отрезок «мои братья» должен быть в два раза больше, чем отрезок «мои сестры». Здесь отрезок «мои братья» (братья девочки) изображает неизвестное число всех мальчиков.
ММои братья Мои сестры
№ 1
ДМои братья Мои сестры
№ 2
Мальчики Девочки
ВСЕ ДЕТИ
?
Рисунок 10
Так как общее число мальчиков и девочек вполне определенное (хотя еще и неизвестное), то длина всей диаграммы № 1 равна длине всей диаграммы № 2. Пусть мальчик и девочка «уйдут» из диаграмм. Сомкнем отрезки на каждой диаграмме. Образовались две новые диаграммы (рисунок 11) опять-таки одинаковой длины.
Братья мальчика Сестры мальчика
№ 1 ½ оставшихся детей
1/2 - 1/3= 1/6
1/3 оставшихся детей
№ 2 Братья девочки Сестры
девочки
Все дети без одного
?
Рисунок 11
Если ушел мальчик, то девочки (красный отрезок) составляют половину общего числа оставшихся детей: если же ушел не мальчик, а ушла девочка, то теперь девочки (красный отрезок) составляют только одну треть того же числа. Отсюда следует, что разность красных отрезков на рисунке 11 изображает одну девочку, которая составляет
1/2 - 1/3 = 1/6 часть от общего числа всех детей, уменьшенного на единицу.
Отсюда общее количество всех детей без одного равно 6. Всего детей 6 + 1 = 7. Из них девочек  мальчиков 7 - 3 = 4.
мальчиков 7 - 3 = 4.
Ответ: 3 девочки и 4 мальчика.
Задача 2.1.2
Коля уплатил в кассу столовой за три блюда, а Саша - за два блюда (все пять блюд одинаковой стоимости). Только они сели за стол, как к ним присоединился Юра, и они втроем съели поровну все пять блюд. При расчете приятелей между собой выяснилось, что Юра должен уплатить за съеденное им 50 рублей. Сколько из этих денег следует Коле и сколько Саше?
Решение.
На листке клетчатой бумаги изобразим условие задачи в виде диаграммы. Зная, что за полную стоимость обеда придется разделить поровну между всеми тремя приятелями, изобразим стоимость каждого блюда отрезком длиною в три клетки (рисунок 12).
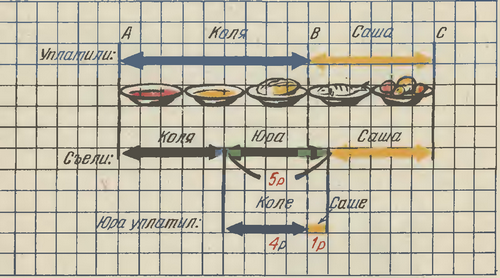
50 р
10 р
40 р
Рисунок 12
Отрезок АВ - стоимость трех блюд, оплаченных Колей, отрезок ВС - стоимость двух блюд, оплаченных Сашей. Следовательно, отрезок АС - стоимость пяти блюд, съеденных всеми тремя.
По условию задачи, доля стоимости всего обеда Юры составляет 50 рублей. Сколько из них он должен отдать Коле и сколько Саше?
Ответ легко получить на самой диаграмме. Разделим отрезок АС на три равные части. Каждая часть изображает стоимость съеденного каждым из приятелей. Пусть средний из них изображает долю Юры - 50 рублей. Диаграмма показывает, что каждая клеточка на рисунке обозначает 10 рублей. Проведем через точку В вертикальную прямую. Она разделит средний из трех отрезков на две части - левую, длиной 4 клетки, примыкающую к доле Коли, и правую- длиной в 1 клетку, примыкающую к доле Саши. Следовательно, Коля должен получить с Юры 40 рублей, а Саша - 10 рублей.
Этот результат, полученный наглядным геометрическим способом, можно проверить при помощи вычислений.
Юра заплатил за долю обеда 50 рублей. Следовательно, полная стоимость всего обеда 50  3 = 150 рублей.
3 = 150 рублей.
Стоимость одного блюда равна 150 : 5 = 30 рублей.
Коля уплатил в кассу 30  3 = 90 рублей.
3 = 90 рублей.
Саша уплатил в кассу 30  2 = 60 рублей.
2 = 60 рублей.
Следовательно, Юра должен отдать Коле 90 - 50 = 40 рублей, Саше 60 - 50 = 10 рублей.
Ответ: 40 рублей и 10 рублей.
Задача 2.1.3 (задача Л. Н. Толстого)
Артели косцов надо было скосить два луга - один вдвое больше другого. Половину дня вся артель косила большой луг. После полудня артель разделилась пополам: первая половина осталась на большом лугу и докосила его к вечеру до конца, а вторая половина косила малый луг, на котором к вечеру остался участок, скошенный на другой день одним косцом, проработавшим целый день. Сколько косцов было в артели?
Решение.
Обозначим число косцов К. за первую половину дня К косцов скосят на большом лугу площадь, которую изобразим прямоугольником с высотой, равной К. Основание прямоугольника обозначим через А (оно произвольное).
За вторую половину дня половина косцов, т.е.  К, скосит на том же лугу площадь, соответствующую прямоугольнику со сторонами А и
К, скосит на том же лугу площадь, соответствующую прямоугольнику со сторонами А и  К. Следовательно, левый составной прямоугольник соответствует площади большого луга. Высота этого прямоугольника
К. Следовательно, левый составной прямоугольник соответствует площади большого луга. Высота этого прямоугольника  К (рисунок 13).
К (рисунок 13).
Большой луг Малый луг


1 + 2
+ 2
12
К
А А
Рисунок 13
За вторую половину первого дня  К косцов скосят на малом лугу площадь, соответствующую прямоугольнику со сторонами А и
К косцов скосят на малом лугу площадь, соответствующую прямоугольнику со сторонами А и  К. За две половины второго дня один косец скосит на втором лугу площадь, соответствующую прямоугольнику, одна сторона которого по-прежнему А, а другая равна 1+1=2. Правый составной прямоугольник имеет высоту
К. За две половины второго дня один косец скосит на втором лугу площадь, соответствующую прямоугольнику, одна сторона которого по-прежнему А, а другая равна 1+1=2. Правый составной прямоугольник имеет высоту  К + 2. И соответствует площади малого луга. По условию малый луг в два раза меньше большого луга. Значит,
К + 2. И соответствует площади малого луга. По условию малый луг в два раза меньше большого луга. Значит,  К + 2 =
К + 2 = 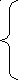 или
или  К = 2. Отсюда число косцов К = 8.
К = 2. Отсюда число косцов К = 8.
Ответ: 8 косцов.
2.2 Применение двумерных диаграмм в решении арифметических задач
На примере решения задачи 2.2.1 покажем два возможных способа применения двумерных диаграмм, а так же приведем алгебраический способ решения этой задачи.
Задача 2.2.1
Поезд проходит расстояние от города А до города В за 10 часов 40 минут. Если бы скорость поезда была на 10 км/ч меньше, то он пришел бы вВ на 2 часа 8 минут позже. Определить расстояние между городами и скорость поезда.
Первый способ (графико-вычислительный). Сделаем чертеж (рисунок 14)
P Q
В
Р
Е
М
Я
2 ч 8 мин
RL M
10 км/ч10 ч 40 мин
O N K
СКОРОСТЬ
Рисунок 14
Пусть в первом случае, предусмотренном в условии задачи, продолжительность хода поезда 10 ч 40 мин изображается отрезком OL, а скорость поезда (ее величина нам пока неизвестна) - отрезком ОК. Тогда площадь прямоугольника OLMK соответствует расстоянию между городами А и В.
Пусть во втором случае скорость поезда изображается отрезком ON, а соответствующее время 10 ч 40 мин + 2 ч 8 мин - отрезком ОР. В этом случае то же расстояние между городами А и В определяется площадью прямоугольника OPQN, равновеликого прямоугольнику OLMK. А если это так, то, на основании выше доказанной вспомогательной теоремы должно быть NL || MQ и тогда треугольники OLN и RQM подобны. Из их подобия следует:
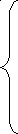 или
или
Получаем, что ON = 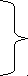 .
.
10 ч 40 мин + 2 ч 8 мин = 12 ч 48 мин = 12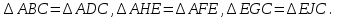 ч.Значит, расстояние между городами равно 50
ч.Значит, расстояние между городами равно 50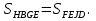
Путь к этому простому арифметическому решению помогла найти геометрия. Алгебраическое решение задачи потребовало более длительных вычислений. Приведем его для сравнения. Пусть S - расстояние между городами А и В. Тогда скорость поезда в первом случае 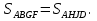 Составляем уравнение:
Составляем уравнение: 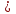 .
.
Решив это уравнение, мы найдем расстояние между городами А и В, но вычисления в этом случае достаточно громоздкие. Не проще будут вычисления, если в качестве неизвестной величины взять скорость поезда.
Второй способ (конструктивное решение). Ответ можно получить не только путем вычислений, но и непосредственно на диаграмме (принято говорить - снять его с диаграммы).
Для решения необходим лист миллиметровой бумаги. Выбрав масштаб для изображения времени и скорости (например, 1 час = 6 мм и 1 км/ч = 1 мм), построим прямоугольный треугольникQRM, у которого в соответствии с выбранными масштабами вертикальный катет RQ изображает 2 часа 8 минут (отрезок RQ = 2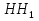 , а горизонтальный катет RM изображает 10 км/ч (длина отрезка RM = 10 мм) (рисунок 15).
, а горизонтальный катет RM изображает 10 км/ч (длина отрезка RM = 10 мм) (рисунок 15).
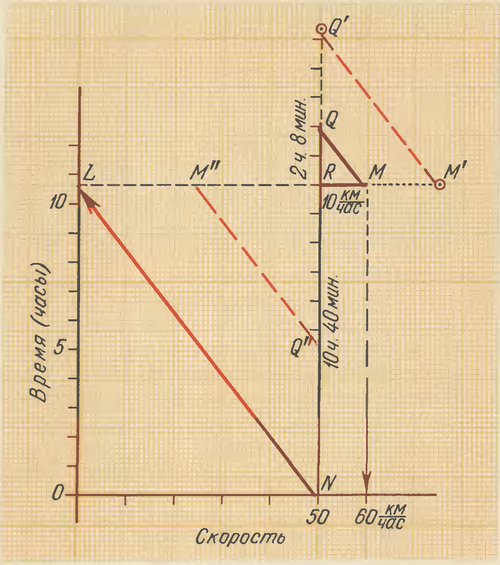
Рисунок 15
Продолжим катеты QRи MR вниз и влево за точку R и отложим отрезок RN, изображающий 10 ч 40 мин (RN = 64 мм). Через точку N проведем прямую NL, параллельную MQ, до пересечения в точке Lc продолжением MR. Тогда отрезок LR изобразит искомую скорость поезда. По масштабу определяем, что она равна 50 км/ч.
В этом решении ответ на задачу получился только при помощи построений с выполнением чертежа в масштабе. Такое решение называется конструктивным.
Ответ: 50 км/ч, 640 км.
Решим еще одну арифметическую задачу с помощью двумерной диаграммы.
Задача 2.2.2
Для выполнения работ поставили 57 рабочих, которые могли окончить работу за 45 дней. Но через 15 дней добавили еще нескольких рабочих, и работа была закончена на 12 дней раньше. Сколько рабочих добавили?
Решение.
Решим задачу графико-вычислительным способом (рисунок 16) .
Рисунок 16
Выполненная работа прямо пропорциональна числу рабочих и числу рабочих дней, отработанных каждым из них. Следовательно, всю работу можно изобразить в виде прямоугольника ОАВС со сторонами ОА (57 рабочих) и ОС (45 дней). По условию, через 15 дней (т.е когда была выполнена работа, изображаемая прямоугольником OADE, где отрезок ОЕ обозначает 15 дней) добавили х рабочих. Оставшаяся часть работы изображается прямоугольником EDBC, где ЕС обозначает 45 - 15 = 30 дней. После того как добавили х рабочих, работа была закончена на 12 дней раньше срока, т.е. через 30 - 12 = 18 дней (EF на диаграмме обозначает 18 дней). Значит, второй период работ изобразится прямоугольником EHGF (где EH обозначает (57 + х) рабочих), равновеликим прямоугольнику EDBC. Но у этих двух прямоугольников есть общая часть - прямоугольник EDJF. Отсюда получается, что прямоугольники FJBC и DHGJ равновелики. Следовательно, 57 
Ответ: 38 рабочих.
Диаграммными методами так же можно решать арифметические задачи на переливание, наследство, сплавы, скорости, работу и многие другие.
ЗАКЛЮЧЕНИЕ
В ходе проведенного исследования я изучила литературу по рассматриваемой теме, научилась строить одномерные (линейные) и двумерные диаграммы, изображая подходящими геометрическими фигурами численные значения величин, входящих в условие задачи, познакомилась с графико-вычислительным и конструктивным методами решения арифметических задач. В работе рассмотрены несколько задач, в решении которых применены диаграммы, а так же их алгебраическое решение. Проведен сравнительный анализ полученных решений арифметических задач. Следует заметить, что конструктивный метод не всегда удобен в применении, так как требует наличие под рукой миллиметровой бумаги и очень точные построения, что не всегда возможно сделать.
Выдвинутая нами гипотеза нашла свое подтверждение. Используя диаграммный метод, можно решить арифметическую задачу, не проводя громоздких вычислений.
Таким образом, мы пришли к следующим выводам:
-
диаграммный метод решения арифметических задач нагляден, что позволяет «увидеть и снять» решение;
-
используя диаграммный метод, можно получить экономные и изящные решения;
-
непосредственное применение изложенный материал может иметь не только на уроках математики, на олимпиадах и конкурсах, но и в практической деятельности.
Существуют другие геометрические методы решения арифметических задач. В частности с применением графика линейной функции, графика равномерного движения, ломаных графиков, с помощью дополнительных построений к графикам. А это значит, что мои исследования геометрической арифметики будут продолжены.
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
-
Александров И. И., Александрова А. И. Методы решения арифметических задач.М.: Физматгиз, 1953
-
Березанская Е. С. Сборник задач и упражнений по арифметике.М.: Физматгиз, 1950
-
Депман И.Я. За страницами учебника математики. М.. Просвещение, 1989
-
Островский А. И., Кордемский Б. А. Геометрия помогает арифметике. М.: Физматгиз, 1960
-
Энциклопедический словарь юного математика. М.: Педагогика, 1985