Экзаменационный материал по математике для групп СПО.

Согласовано: Утверждаю:

</ Заведующая МК ЕНЦ Директор ГАПОУ МО ППТ

_______ О.М.Седова __________Е.А.Будахина

Протокол №_____от _______2016 г. «___»___________2016 г.

Экзаменационный материал

к итоговой аттестации по предмету

«Математика: алгебра и начала математического анализа, геометрия»

для групп ДО-15 ; 215 ; 218 .

Вариант 1.

Часть 1.

1. Вычислите: 0,36+32^4/5

2. Найдите область определения функции: у =

3. Найдите корень уравнения: 3^4х+1 = 9

4. Закончите запись:

5. Решите неравенство: ()^х-3 <

6. Найдите корень уравнения: log₂(x+1) = log₂32 - log₂8

7. Вычислить: sin 30⁰ + 2cos 45⁰

8. Решите неравенство: log_0,3х-1 ≥ 0

9. Определите, какая фигура получается при пересечении прямой треугольной призмы плоскостью, перпендикулярной основанию призмы.

10. Найдите нули функции: у = х²- 121 .

11. Решите уравнение: sin х + = 0

12. Найдите производную функции: y = 3х⁴-+5

13. Найдите все первообразные функции: f(х) = х⁵+2х

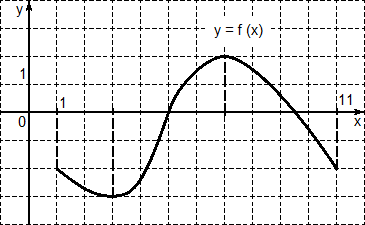
14. Укажите промежуток возрастания функции y = f(x),заданной графиком.

Часть 2.

1. Найдите наибольшее значение функции f(x) = - 3x на отрезке [0; 3]

2. Решите уравнение: = х

3. Найдите объём тела, полученного при вращении прямоугольного треугольника с гипотенузой 41см и катетом 9 см вокруг большего катета.

4. Найдите площадь полной поверхности правильной четырёхугольной призмы

со стороной основания 3 см и высотой 14 см.

Вариант 2.

Часть 1.

1. Вычислите: 81^3/4 - 0,56

2. Найдите область определения функции: y =

3. Найдите корень уравнения: 2^2х+3 = 8

4. Закончите запись:

5. Решите неравенство: 3^4+х >

6. Найдите корень уравнения: log₃(3-х) = log₃14-log₃7

7. Вычислить: cos 60⁰ + 4sin 45⁰

8. Решите неравенство: 1-log_0,5х ≥ 0

9. Определите, какая фигура получается при пересечении правильной четырёхугольной пирамиды

плоскостью, содержащей высоту пирамиды.

10. Найдите нули функции: у = х²- 144 .

11. Решите уравнение: cos х + = 0

12. Найдите производную функции: y =-3х⁵

13. Найдите все первообразные функции: f(х) = х⁴-2х

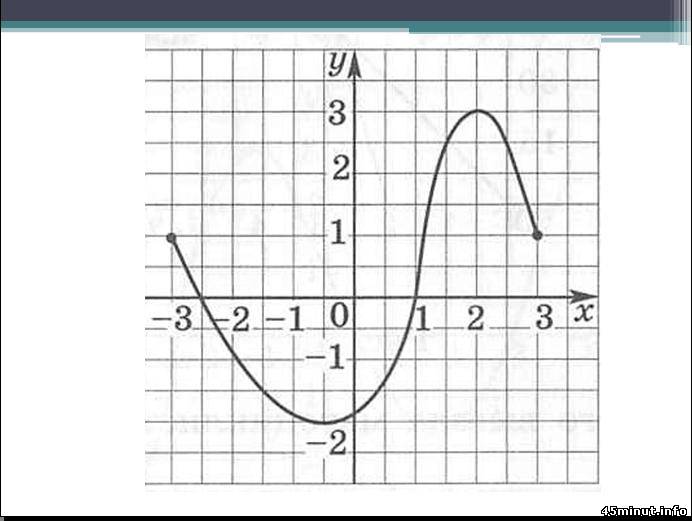
14. Укажите промежуток убывания функции y = f(x),заданной графиком.

Часть 2.

1. Найдите наибольшее значение функции f(x) = 3x- на отрезке [-3; 0]

2. Решите уравнение: = х

3. Найдите объём тела, полученного при вращении прямоугольника площадью 36 см²

и стороной 9 см вокруг меньшей стороны.

4. Найдите площадь полной поверхности правильной треугольной пирамиды

со стороной основания 3 см и апофемой 16 см.

Вариант 3.

Часть 1.

1. Вычислите: 9^3/2 + 1,5

2. Найдите область определения функции: у =

3. Найдите корень уравнения: 5^2х+1 = 125

4. Закончите запись:

5. Решите неравенство: 2^1-х > 8

6. Найдите корень уравнения: log₅(3x) = log₅4+log₅8

7. Вычислить: 6sin 45⁰ + cos 60⁰

8. Решите неравенство: 1-log_0,1х ≥ 0

9. Определите, какая фигура получается при пересечении прямой треугольной призмы плоскостью, параллельной основанию призмы.

10. Найдите нули функции: у = х²- 225 .

11. Решите уравнение: - = 0

12. Найдите производную функции: y = -2х⁴ -cos x+3

13. Найдите все первообразные функции: f(х) = 3х²-х⁶

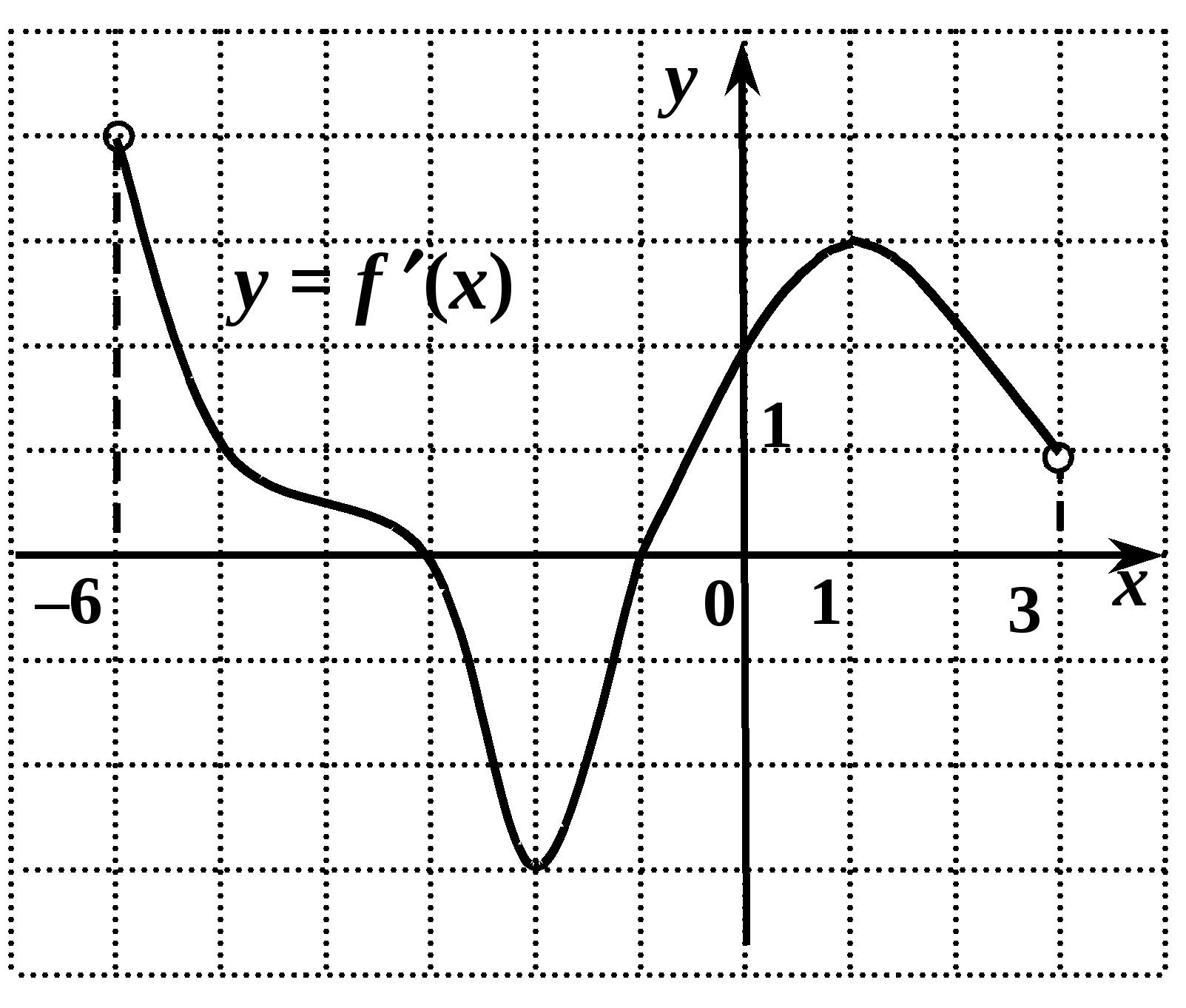
14. Укажите промежуток возрастания функции y = f(x),заданной графиком.

Часть 2.

1. Найдите наименьшее значение функции f(x) = 12х - 4 на отрезке [-3; 0]

2. Решите уравнение: = х

3. Найдите объём тела, полученного при вращении прямоугольного треугольника с

гипотенузой 29 см и катетом 21 см вокруг меньшего катета.

4. Найдите площадь полной поверхности правильной четырёхугольной призмы

со стороной основания 4 см и высотой 8 см.

Вариант 4.

Часть 1.

1. Вычислите: 27^2/3 - 0,15

2. Найдите область определения функции: y =

3. Найдите корень уравнения: 2^5х+1 = 4

4. Закончите запись:

5. Решите неравенство: ( )^х+3 ≥

6. Найдите корень уравнения: log₃(6x) = log₃20-log₃4

7. Вычислить: 10cos 45⁰ + sin 30⁰

8. Решите неравенство: log_0,5х+1 ≥ 0

9. Определите, какая фигура получается при пересечении правильной четырёхугольной пирамиды плоскостью, перпендикулярной высоте пирамиды.

10. Найдите нули функции: у = х²- 196 .

11. Решите уравнение: sin х - = 0

12. Найдите производную функции: y = -3х⁴ +5

13. Найдите все первообразные функции: f(х) = 4х³+х²

14. Укажите промежуток убывания функции y = f(x),заданной графиком.

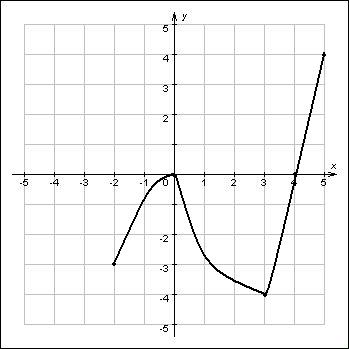
Часть 2.

1. Найдите наименьшее значение функции f(x) = 2 - 6х на отрезке [0; 2]

2. Решите уравнение: = х

3. Найдите объём тела, полученного при вращении прямоугольника площадью 32см²

и стороной 8 см вокруг меньшей стороны.

4. Найдите площадь полной поверхности правильной треугольной пирамиды

со стороной основания 4 см и апофемой 14 см.

Вариант 5.

Часть 1.

1. Вычислите: 8^5/3 - 0,21

2. Найдите область определения функции: у =

3. Найдите корень уравнения: 5^х+3 = 125

4. Закончите запись:

5. Решите неравенство: 2^х+1 ≥

6. Найдите корень уравнения: log₇(x+18) = log₇9+log₇2

7. Вычислить: 8sin 45⁰ + cos 60⁰

8. Решите неравенство: log_0,5х-1 ≥ 0

9. Определите, какая фигура получается при пересечении цилиндра плоскостью, параллельной основанию цилиндра.

10. Найдите нули функции: у = х²- 441 .

11. Решите уравнение: cos х - = 0

12. Найдите производную функции: y = +6х²

13. Найдите все первообразные функции: f(х) = 4x-х³

14. Укажите промежуток убывания функции y = f(x),заданной графиком.

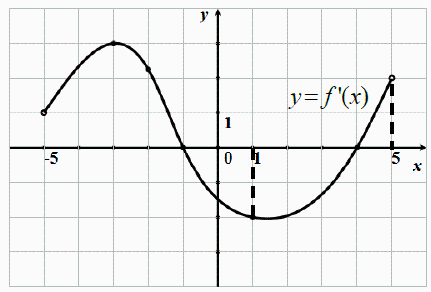
Часть 2.

1. Найдите наибольшее значение функции f(x) = - 12x на отрезке [0; 3]

2. Решите уравнение: = х

3. Найдите объём тела, полученного при вращении прямоугольного треугольника с

гипотенузой 26 см и катетом 24 см вокруг меньшего катета.

4. Найдите площадь полной поверхности правильной четырёхугольной призмы

со стороной основания 5 см и высотой 12 см.

Вариант 6.

Часть 1.

1. Вычислите: 32^6/5 - 0,7

2. Найдите область определения функции: y =

3. Найдите корень уравнения: 6^2х+2 = 216

4. Закончите запись:

5. Решите неравенство: (1/6)^х+1 ≤ 36

6. Найдите корень уравнения: log₃(4x+8) = log₃5+log₃2

7. Вычислить: 12cos 45⁰ + sin 30⁰

8. Решите неравенство: 2-log₂х ≥ 0

9. Определите, какая фигура получается при пересечении конуса плоскостью, перпендикулярной

основанию конуса.

10. Найдите нули функции: у = 324 - х² .

11. Решите уравнение: sin х + = 0

12. Найдите производную функции: y = 9-9х⁸+

13. Найдите все первообразные функции: f(х) = 5х⁴-8х

14. Укажите промежуток возрастания функции y = f(x),заданной графиком.

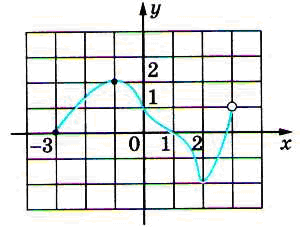
Часть 2.

1. Найдите наименьшее значение функции f(x) = - 9x на отрезке [0; 2]

2. Решите уравнение: = х

3. Найдите объём тела, полученного при вращении прямоугольника площадью 30см²

и стороной 6 см вокруг большей стороны.

4. Найдите площадь полной поверхности правильной четырёхугольной пирамиды

со стороной основания 3 см и апофемой 8 см.

Вариант 7.

Часть 1.

1. Вычислите: 16^5/4 + 1,25

2. Найдите область определения функции: у =

3. Найдите корень уравнения: 7^2х+2 = 343

4. Закончите запись:

5. Решите неравенство: ()^х+2 ≥ 4

6. Найдите корень уравнения: log₃(x+1) = log₃10-log₃5

7. Вычислить: 4sin 30⁰ + cos 60⁰

8. Решите неравенство: 3- log₄х ≥ 0

9. Определите, какая фигура получается при пересечении цилиндра плоскостью, перпендикулярной

высоте цилиндра.

10. Найдите нули функции: у = 289 - х² .

11. Решите уравнение: cos х - = 0

12. Найдите производную функции: y = 4х³+cos x-5

13. Найдите все первообразные функции: f(х) = 6x+х⁴

14. Укажите промежуток убывания функции y = f(x),заданной графиком.

Часть 2.

1. Найдите наибольшее значение функции f(x) = на отрезке [-2; 0]

2. Решите уравнение: = х

3. Найдите объём тела, полученного при вращении прямоугольного треугольника с

гипотенузой 25 см и катетом 20 см вокруг меньшего катета.

4. Найдите площадь полной поверхности правильной треугольной призмы

со стороной основания 5 см и высотой 10 см.

Вариант 8.

Часть 1.

1. Вычислите: 4^5/2 - 0,75

2. Найдите область определения функции: y =

3. Найдите корень уравнения: 3^3х+3 = 9

4. Закончите запись:

5. Решите неравенство: 5^3-x < 1/25

6. Найдите корень уравнения: log₅(13-x) = log₅3+log₅4

7. Вычислить: 16cos 30⁰ + sin 30⁰

8. Решите неравенство: 2-log₅х ≥ 0

9. Определите, какая фигура получается при пересечении цилиндра плоскостью, перпендикулярной

основанию цилиндра.

10. Найдите нули функции: у = 256 - х² .

11. Решите уравнение: sin х + = 0

12. Найдите производную функции: y = cos x+5х³+4

13. Найдите все первообразные функции: f(х) = х³+7х⁶

14. Укажите промежуток возрастания функции y = f(x),заданной графиком.

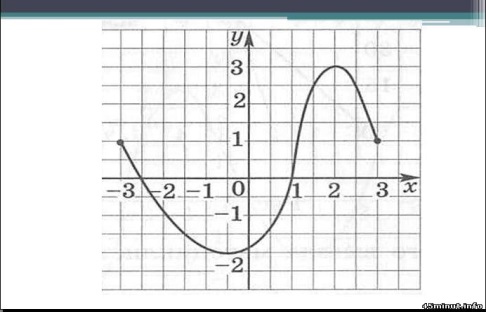
Часть 2.

1. Найдите наименьшее значение функции f(x) = - 15x на отрезке [0; 3]

2. Решите уравнение: = х

3. Найдите объём тела, полученного при вращении прямоугольника площадью 24см²

и стороной 6 см вокруг меньшей стороны.

4. Найдите площадь полной поверхности правильной четырёхугольной пирамиды

со стороной основания 4 см и апофемой 12 см.

Вариант 9.

Часть 1.

1. Вычислите: 64^5/6 +0,26

2. Найдите область определения функции: у =

3. Найдите корень уравнения: 2^3х+1 = 8

4. Закончите запись:

5. Решите неравенство: ( )^х-2 > 27

6. Найдите корень уравнения: log₅(16-x) = log₅2+log₅6

7. Вычислить: cos 60⁰ + 20sin 60⁰

8. Решите неравенство: 5- log₂2x ≥ 0

9. Определите, какая фигура получается при пересечении конуса плоскостью, параллельной

основанию конуса.

10. Найдите нули функции: у = 529 - х² .

11. Решите уравнение: cos х + = 0

12. Найдите производную функции: y = 5-cos x-3х⁶

13. Найдите все первообразные функции: f(х) = 8x+х²

14. Укажите промежуток убывания функции y = f(x),заданной графиком.

Часть 2.

15. Найдите наибольшее значение функции f(x) = на отрезке [-2; 0]

16. Решите уравнение: = х

17. Найдите объём тела, полученного при вращении прямоугольного треугольника с

гипотенузой 20 см и катетом 16 см вокруг меньшего катета.

18. Найдите площадь полной поверхности правильной треугольной призмы

со стороной основания 4 см и высотой 15 см.

Вариант 10.

Часть 1.

1. Вычислите: 125^2/3 - 0,25

2. Найдите область определения функции: y =

3. Найдите корень уравнения: 4^х+6 = 1

4. Закончите запись:

5. Решите неравенство: ( )^2-х ≤

6. Найдите корень уравнения: log₅(8x) = log₅27-log₅3

7. Вычислить: 14sin 30⁰ + 2cos 60⁰

8. Решите неравенство: 2+log_0,5х ≥ 0

9. Определите, какая фигура получается при пересечении правильной четырёхугольной пирамиды плоскостью, параллельной основанию пирамиды.

10. Найдите нули функции: у = 361 - х² .

11. Решите уравнение: sin х - = 0

12. Найдите производную функции: y = 7х⁵

13 Найдите все первообразные функции: f(х) = 5х⁴-х³

14. Укажите промежуток возрастания функции y = f(x),заданной графиком.

Часть 2.

1. Найдите наибольшее значение функции f(x) = на отрезке [-3; 0]

2. Решите уравнение: = х

3. Найдите объём тела, полученного при вращении прямоугольника площадью 28см²

и стороной 4 см вокруг большей стороны.

4. Найдите площадь полной поверхности правильной треугольной пирамиды

со стороной основания 5 см и апофемой 18 см.

Инструкция по выполнению работы.

На выполнение экзаменационной работы даётся 3 часа (180 минут).

В работе 18 заданий. Они распределены на две части. Из 18 заданий каждого варианта четыре задания по геометрии, остальные по алгебре и началам анализа.

Часть 1 содержит 14 заданий обязательного уровня по материалу курса «Математика: алгебра и начала анализа, геометрия». При выполнении этих заданий надо указать в бланке верный ответ.

Часть 2 содержит 4 задания повышенного уровня по материалу курса «Математика: алгебра и начала анализа, геометрия», а также различных разделов курса геометрии. К заданиям второй части надо дать краткое решение.

Советуется выполнять задания в том порядке, в котором они даны. Для экономии времени пропускайте задание, которое не удаётся выполнить сразу, и переходите к следующему. Если после выполнения всей работы у вас останется время, то можно вернуться к пропущенным заданиям.

Итоговый балл выставляется по 22-балльной шкале на основе первичных баллов, полученных за выполнение всех заданий работы. За верное выполнение различных по сложности заданий даётся один или более баллов. Баллы, полученные вами за все выполненные задания, суммируются. Постарайтесь выполнить как можно больше заданий и набрать как можно большее количество баллов.

Критерии оценки выполнения заданий.

Каждое правильно выполненное задание 1 части оценивается 1 баллом. Каждое выполненное задание 2 части оценивается баллами в зависимости от выполнения задания:

1 балл - общая идея, способ решения верные, но решение не завершено. Допустимы негрубые ошибки в вычислениях и преобразованиях, не влияющие на правильность дальнейшего хода решения. В результате этих ошибок возможен неверный ответ.

2 балла - задание решено верно с обоснованием решения.

Максимальное число первичных баллов, которое можно получить за верное решение всех заданий, равно 22 баллам.

Шкала перевода первичных баллов в пятибалльную оценку.Первичные

баллы

0 - 9

10 - 12

13 - 17

18 - 22

Аттестационная

отметка

2

3

4

5

Подготовительный вариант.

I вариант.

Часть 1.

1. Вычислите: 0,64+8^4/3

2. Найдите область определения функции: y =

3. Найдите корень уравнения: 4^3х+1=64

4. Закончите запись:

5. Решите неравенство: 4^5-x < 1/16

6. Найдите корень уравнения: log₄(3x+6) = log₄24-log₄2

7. Вычислите: 18cos 60⁰ - 8sin 60⁰

8. Решите неравенство: log_0,4х-1 ≥ 0

9. Определите, какая фигура получается при пересечении правильной четырёхугольной призмы плоскостью, параллельной основанию призмы.

10. Найдите нули функции: у = 576 - х² .

11. Решите уравнение: sin х - = 0

12. Найдите производную функции: y = 7+8х⁹-

13. Найдите все первообразные функции: f(х) = 6х⁵+х³

14. Укажите промежуток убывания функции y = f(x),заданной графиком.

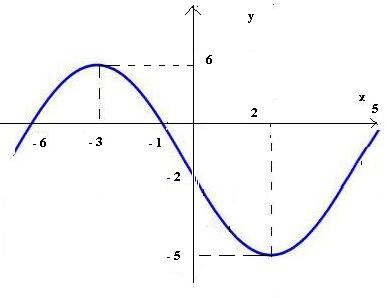
Часть 2.

1. Найдите наибольшее значение функции f(x) = на отрезке [-3; 0]

2. Решите уравнение: х =.

3. Найдите объём тела, полученного при вращении прямоугольного треугольника с

гипотенузой 13 см и катетом 5 см вокруг большего катета.

4. Найдите площадь полной поверхности правильной треугольной пирамиды

со стороной основания 3 см и апофемой 12 см.

Подготовительный вариант.

II вариант.

Часть 1.

1. Вычислите: 27^4/3- 0,35

2. Найдите область определения функции: y =

3. Найдите корень уравнения: 6^4х+6 = 36

4. Закончите запись:

5. Решите неравенство: (1/3)^х+4 > 9.

6. Найдите корень уравнения: log₂(15-x) = log₂6+log₂3

7. Вычислите: 16sin 30⁰ + 4cos 60⁰

8. Решите неравенство: 4- log₃х ≥ 0

9. Определите, какая фигура получается при пересечении цилиндра плоскостью, параллельной высоте цилиндра.

10. Найдите нули функции: у = 625 - х² .

11. Решите уравнение: cos х + = 0

12. Найдите производную функции: y = -3х⁵-4

13. Найдите все первообразные функции: f(х) = 6x-5х⁴

14. Укажите промежуток возрастания функции y = f(x),заданной графиком

Часть 2.

1. Найдите наибольшее значение функции f(x) = на отрезке [0; 3]

2. Решите уравнение: х =.

3. Найдите объём тела, полученного при вращении прямоугольника площадью 90 см² и стороной

9 см вокруг меньшей стороны.

4. Найдите площадь полной поверхности правильной четырёхугольной призмы

со стороной основания 11 см и высотой 15 см.