Доказательство четвертого признака равенства треугольников

Четвертый признак равенства треугольников

- Четвертый признак звучит так: «Если две стороны и угол, лежащий против большей из них одного треугольника соответственно равны двум сторонам и углу, лежащему против большей из них другого треугольника, то такие треугольники равны».

- Попробуйте доказать данный признак самостоятельно, используя условие и алгоритм. Для доказательства равенства треугольников, расположите их так, как показано на рисунке 2.

Дано: ∆ АВС, ∆ А1В1С1,

АВ = А₁ В₁,

АС= А₁ С₁.,

ے В = ے В₁

Доказать:

∆ АВС = ∆ А₁В₁С₁.

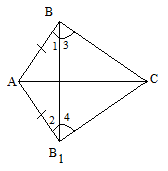рис.2

1. Рассмотрите треугольник ВАВ₁ и докажите, что ے1 = ے2;

2. Рассмотрите треугольник ВСВ₁, докажите равенство ے3 и ے4. Определите вид треугольника ВСВ₁.

3. Докажите равенство треугольников АВС и

А₁В₁С₁.

Проверьте себя!

1) ∆АВВ₁- равнобедренный, значит ے 1= ے 2.

2) ے 3= ے 4 как остатки равных углов.

3) Получим ∆ВСВ₁ - равнобедренный, отсюда ВС = В₁С.

4) ∆АВС=∆А₁В₁С₁ по трем сторонам.