Рабочая программа и ИКТ по геометрии в 8 классе

Государственное казенное общобразовательное учреждение

кадетская школа-интернат «Навигацкая школа» города Москвы

Рассмотрено

на заседании МО

Протокол № ____

от ________________ 2016г.

Руководитель МО

_______________ Тихомирова Л.А.

подпись

Согласованно

Заместитель директора по УР

______________ Королев А.П.

подпись

Утверждаю

Приказ № _____

от ___________________2016 г.

Директор школы

______________ И.Е.Старчеус

подпись

Рабочая программа

Предмет: Геометрии

Класс ____8____.

Профиль: базовый

Всего часов на изучение программы ___70

Количество часов в неделю __2__

Ямилова Д.Р..

Учитель математики

высшая квалификационная категория

2016-2017 учебный год

Пояснительная записка

Учебная программа по геометрии составлена на основе федерального компонента государственного стандарта основного общего образования.

Данная учебная программа ориентирована на учащихся 8 класса и реализуется на основе следующих документов:

1. Государственного стандарта основного общего образования 2004 г.;

2. Базисного учебного плана;

3. Примерной программы общеобразовательных учреждений по геометрии 7-9 классы, к учебному комплекту для 7-9 классов (авторы Л.С. Атанасян, В.Ф. Бутузов, С.В. Кадомцев и др., составитель Т.А. Бурмистрова - М: «Просвещение», 2014. - с. 19-21);

Программа соответствует учебнику Атанася Л. С.. Геометрия: Учебник для 7-9 классов средней школы.- М.: «Просвещение»2014.

Программа рассчитана на 70 часов. Количество часов в неделю-2 часа.

Данная рабочая программа полностью отражает базовый уровень подготовки школьников по разделам программы. Она конкретизирует содержание тем образовательного стандарта и дает примерное распределение учебных часов по разделам курса.

Программа выполняет две основные функции. Информационно-методическая функция позволяет всем участникам образовательного процесса получить представление о целях, содержании, общей стратегии обучения, воспитания и развития учащихся средствами данного учебного предмета. Организационно-планирующая функция предусматривает выделение этапов обучения, структурирование учебного материала, определение его количественных и качественных характеристик на каждом из этапов.

Общая характеристика учебного предмета

Геометрия - один из важнейших компонентов математического образования, она необходима для приобретения конкретных знаний о пространстве и практически значимых умений, формирования языка описания объектов окружающего мира, развития пространственного воображения и интуиции, математической культуры и эстетического воспитания учащихся. Изучение геометрии вносит вклад в развитие логического мышления и формирование понятия доказательства.

Цели

Цели обучения математики в общеобразовательной школе определяются ее ролью в развитии общества в целом и формировании личности каждого отдельного человека.

Программа направлена на достижение следующих целей:

• овладение системой математических знаний и умений, необходимых для применения практической деятельности изучения смежных дисциплин, продолжения образования;

• интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясность и точность мысли, критичность мышления, интуиция, логическое мышление, элементы алгоритмической культуры, пространственных представлений;

• формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;

• воспитание культуры личности, отношения к математике как части общечеловеческой культуры, понимание значимости математики для научно технического прогресса;

• развитие представлений о полной картине мира, о взаимосвязи математики с другими предметами.

В курсе геометрии 8-го класса продолжается решение задач на признаки равенства треугольников, но в совокупности с применением новых теоретических факторов. Теореме о сумме углов выпуклого многоугольника позволяет расширить класс задач. Формируется практические навыки вычисления площадей многоугольников в ходе решения задач. Особое внимание уделяется применению подобия треугольников к доказательствам теорем и решению задач. Даются первые знания о синусе, косинусе и тангенсе острого угла прямоугольного треугольника. Даются учащимся систематизированные сведения об окружности и её свойствах, вписанной и описанной окружностях. Серьезное внимание уделяется формированию умений рассуждать, делать простые доказательства, давать обоснования выполняемых действий. Параллельно закладываются основы для изучения систематических курсов стереометрии, физики, химии и других смежных предметов.

Место предмета

На изучение предмета отводится 2 часа в неделю, итого 70 часов за учебный год.

Результаты обучения

Результаты обучения представлены в Требованиях к уровню подготовки и задают систему итоговых результатов обучения, которых должны достичь

все учащиеся, оканчивающие 8 класс, и достижение которых является обязательным условием положительной аттестации ученика за курс 8 класса. Эти требования структурированы по трем компонентам: знать, уметь, использовать приобретенные знания и умения в практической деятельности и повседневной жизни.

В каждом из разделов уделяется внимание привитию навыков самостоятельной работы.

На протяжении изучения материала предполагается закрепление и отработка основных умений и навыков, их совершенствование, а также систематизация полученных ранее знаний, таким образом, решаются следующие задачи:

• введение терминологии и отработка умения ее грамотного использования;

• развитие навыков изображения планиметрических фигур и простейших геометрических конфигураций;

• совершенствование навыков применения свойств геометрических фигур как опоры при решении задач;

• формирование умения решения задач на вычисление геометрических величин с применением изученных свойств фигур и формул;

• совершенствование навыков решения задач на доказательство;

• отработка навыков решения задач на построение с помощью циркуля и линейки;

• расширение знаний учащихся о треугольниках, четырехугольниках и окружности.

В ходе изучения материала планируется проведение пяти контрольных работ по основным темам.

Содержание обучения

Треугольник. Теорема Фалеса. Подобие треугольников; коэффициент подобия. Признаки подобия треугольников. Теорема Пифагора. Признаки равенства прямоугольных треугольников. Синус, косинус, тангенс, котангенс острого угла прямоугольного треугольника и углов от 0° до 90°. Решение прямоугольных треугольников. Замечательные точки треугольника: точки пересечения серединных перпендикуляров, биссектрис, медиан. Окружность Эйлера.

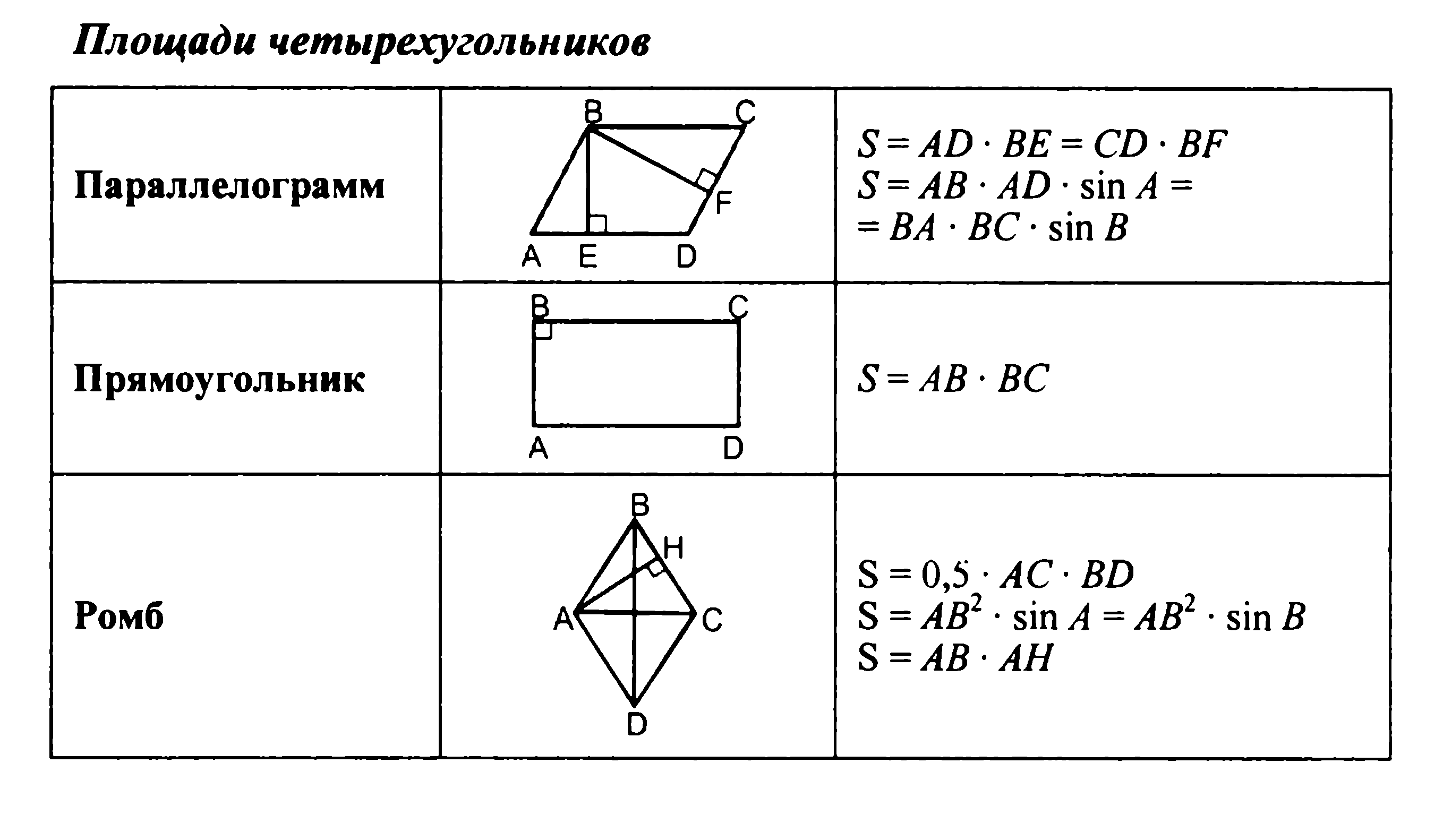
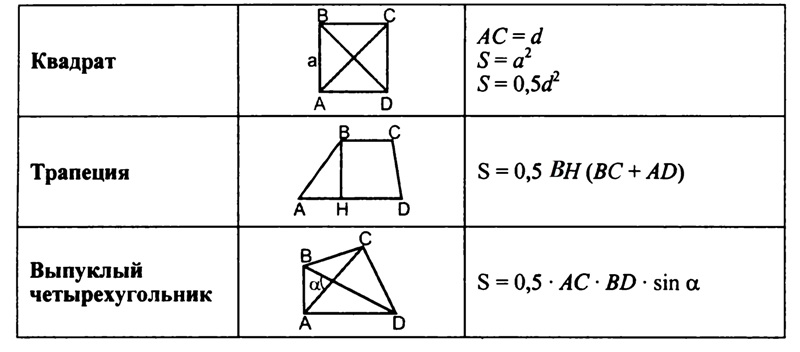
Четырехугольник. Параллелограмм, его свойства и признаки. Прямоугольник, квадрат, ромб, их свойства и признаки. Трапеция, средняя линия трапеции; равнобедренная трапеция.

Окружность и круг. Центр, радиус, диаметр. Центральный, вписанный угол; величина вписанного угла. Взаимное расположение прямой и окружности, двух окружностей. Касательная и секущая к окружности, равенство касательных, проведенных из одной точки. Метрические соотношения в окружности: свойства секущих, касательных, хорд.

Окружность, вписанная в треугольник, и окружность, описанная около треугольника. Вписанные и описанные четырехугольники.

Измерение геометрических величин. Понятие о площади плоских фигур. Равносоставленные и равновеликие фигуры. Площадь прямоугольника. Площадь параллелограмма, треугольника и трапеции (основные формулы). Формулы, выражающие площадь треугольника: через две стороны и угол между ними, через периметр и радиус вписанной окружности, формула Герона. Площадь четырехугольника. Связь между площадями подобных фигур.

Построения с помощью циркуля и линейки. Деление отрезка на п равных частей, построение четвертого пропорционального отрезка.

ТРЕБОВАНИЯ К УРОВНЮ ПОДГОТОВКИ ОБУЧАЮЩИХСЯ

В результате изучения математики ученик должен

уметь

• пользоваться языком геометрии для описания предметов окружающего мира;

• распознавать геометрические фигуры, различать их взаимное расположение;

• изображать геометрические фигуры; выполнять чертежи по условию задач; осуществлять преобразования фигур;

• вычислять значения геометрических величин (длин, углов, площадей), в том числе: для углов от 0˚ до 90˚ определять значения тригонометрических функций по заданным значениям углов; находить значения тригонометрических функций по значению одной из них, находить стороны, углы и площади треугольников, площадей основных геометрических фигур и фигур, составленных из них;

• решать геометрические задачи, опираясь на изученные свойства фигур и отношений между ними, применяя дополнительные построения, алгебраический и тригонометрический аппарат, идеи симметрии;

• проводить доказательные рассуждения при решении задач, используя известные теоремы, обнаруживая возможности для их использования;

Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

• описания реальных ситуаций на языке геометрии;

• расчетов, включающих простейшие тригонометрические формулы;

• решения геометрических задач с использованием тригонометрии;

• решения практических задач, связанных с нахождением геометрических величин (используя при необходимости справочники и технические средства);

• построений геометрическими инструментами (линейка, угольник, циркуль, транспортир).

ГЕОМЕТРИЯ

1. Повторение (1 ч)

Основные понятия. Смежные и вертикальные углы и их свойства. Признаки равенства треугольников. Медианы, биссектрисы и высоты треугольника. Признаки параллельности прямых. Свойства параллельных прямых. Сумма углов треугольника. Свойства, признаки равенства прямоугольных треугольников.

Основная цель - систематизация знаний обучающихся.

В результате изучения темы учащийся должен

знать/понимать

- понятие середины отрезка и биссектрисы угла;

- понятие длины отрезка и ее свойства;

- понятие градуса и градусной меры угла и ее свойства;

- смежные и вертикальные углы и их свойства;

- понятие перпендикулярных прямых и их свойство;

- формулировки и доказательство признаков равенства треугольников;

- понятие перпендикуляра к прямой, медианы, биссектрисы и высоты треугольника, их свойства;

- формулировку теоремы о перпендикуляре;

- понятия равнобедренного и равностороннего треугольников и их свойств;

- понятие окружности и ее элементов;

- понятие параллельных прямых, признаки параллельности двух прямых;

- понятие накрест лежащих, односторонних и соответственных углов;

- аксиому параллельных прямых и ее следствия;

- свойства параллельных прямых

- формулировки теоремы о сумме углов треугольника и ее следствия;

- формулировки теоремы о соотношении между сторонами и углами треугольника и ее следствий;

- формулировка теоремы о неравенстве треугольника;

- понятие прямоугольного треугольника;

- свойства прямоугольных треугольников;

- признак прямоугольного треугольника;

- признаки равенства прямоугольных треугольников;

- понятие перпендикуляра к прямой, наклонной;

- расстояние от точки до прямой, расстояние между параллельными прямыми;

уметь

- строить биссектрису угла;

- находить длины части отрезка (угла) или всего отрезка (угла);

- измерять углы;

- строить угол, смежный с данным углом, вертикальные углы, находить на рисунке смежные и вертикальные углы;

- строить перпендикулярные прямые;

- решать задачи на применение признаков равенства треугольников;

- строить перпендикуляр к прямой, медиану, биссектрису и высоту треугольника;

- применять свойства равнобедренного треугольника на практике;

- строить и находить на чертеже накрест лежащие, односторонние и соответственные углы;

- решать задачи на применение признаков параллельности двух прямых, аксиомы параллельных прямых, свойств параллельных прямых;

- решать задачи на применение теоремы о сумме углов треугольника и ее следствия, теоремы о соотношении между сторонами и углами треугольника и ее следствий, теоремы о неравенстве треугольника, свойств прямоугольных треугольников, признака прямоугольного треугольника, признаков равенства прямоугольных треугольников;

- решать задачи на нахождение расстояния от точки до прямой, расстояния между параллельными прямыми;

- строить и находить на чертеже остроугольные, прямоугольные и тупоугольные треугольники, прямоугольные треугольники;

- решать задачи на построение с помощью циркуля и линейки;

использовать в практической деятельности

- умение решать практические задачи, связанные с нахождением геометрических величин (используя при необходимости справочники, технические средства);

приобретать опыт

- алгоритмической деятельности при составлении математической модели заданной ситуации.

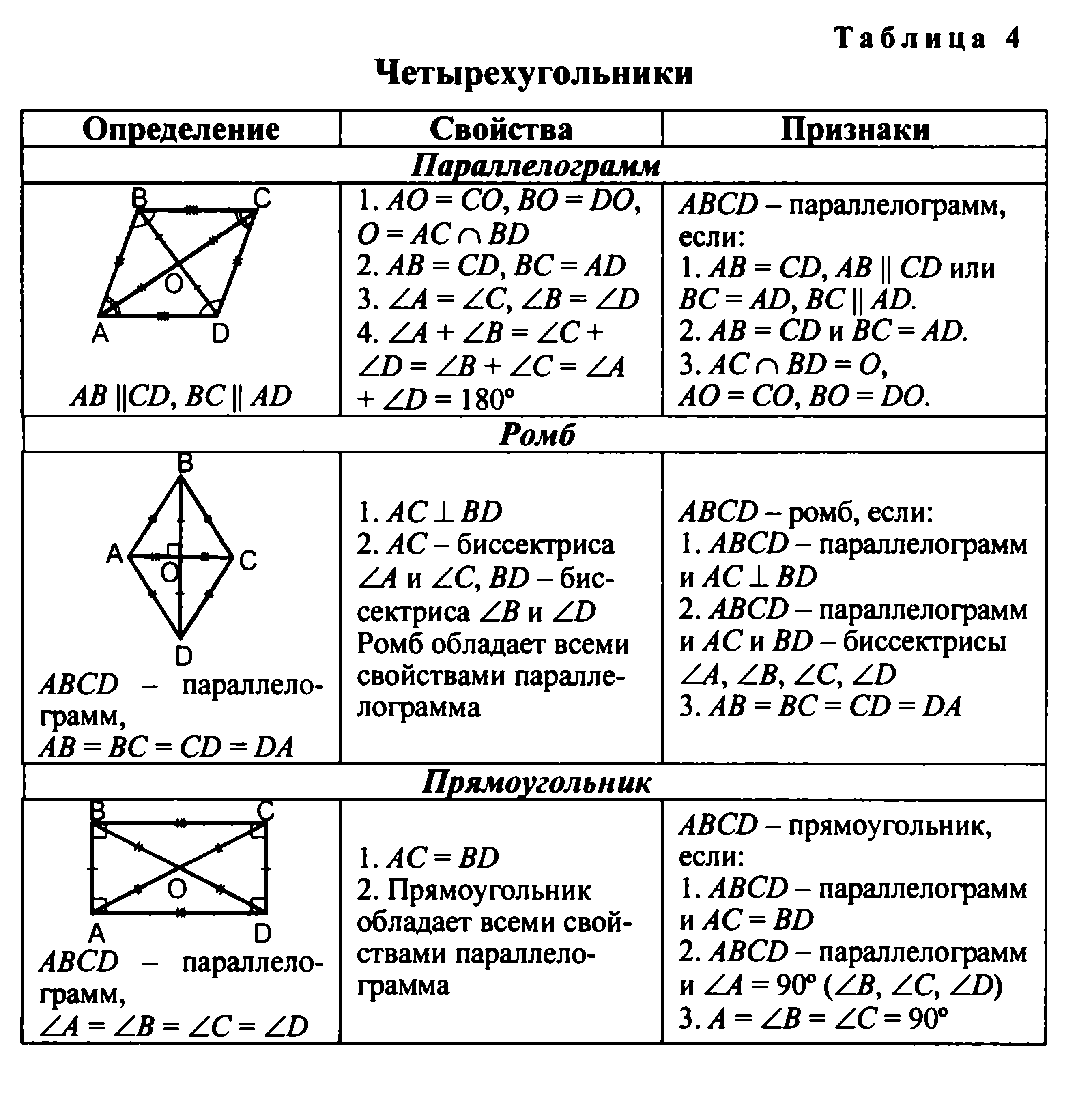
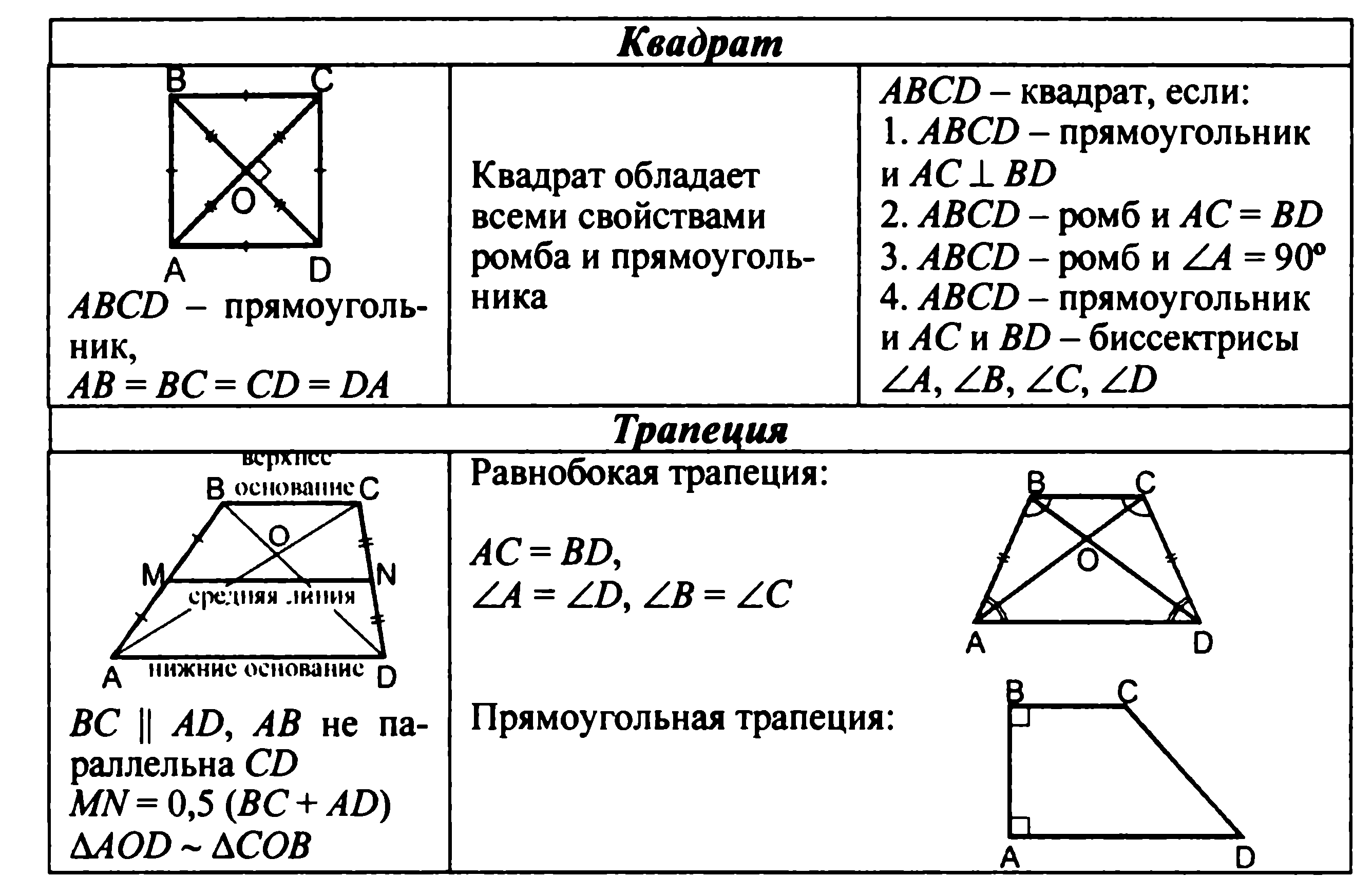
2. Четырехугольники (13 ч)

Основные понятия:

Понятия многоугольника, выпуклого многоугольника. Параллелограмм и его признаки и свойства. Трапеция. Прямоугольник, ромб, квадрат и их свойства. Осевая и центральная симметрии.

Основная цель: дать систематические сведения о четырехугольниках и их свойствах; сформировать представления о фигурах, симметричных, относительно точки или прямой.

В результате изучения темы учащийся должен

знать/понимать

- понятие многоугольника и выпуклого многоугольника, элементов многоугольника, внутренней и внешней области;

- понятие периметра многоугольника;

- формулу суммы углов выпуклого многоугольника;

- понятие параллелограмма, его признаки и свойства;

- понятие трапеции, равнобедренной и прямоугольной трапеции;

- понятие прямой и обратной теоремы;

- понятия прямоугольника, ромба и квадрата, их свойства и признаки;

- понятие симметричных точек и фигур относительно прямой и точки;

уметь

- объяснить, какая фигура называется многоугольником, назвать его элементы;

- выводить и пользоваться формулой суммы углов выпуклого многоугольника;

- доказывать и применять свойства и признаки параллелограмма и трапеции при решении задач;

- доказывать и применять свойства и признаки прямоугольника, ромба и квадрата при решении задач;

- выполнять чертежи по условию задачи;

- делить отрезок на n равных частей с помощью циркуля и линейки;

- решать задачи на построение;

- строить симметричные точки, распознавать фигуры, обладающие осевой и центральной симметрией;

использовать в практической деятельности

- умения строить и исследовать простейших математических моделей;

приобретать опыт

- алгоритмической деятельности при составлении математической модели заданной ситуации.

3. Площади фигур (14 ч)

Основные понятия:

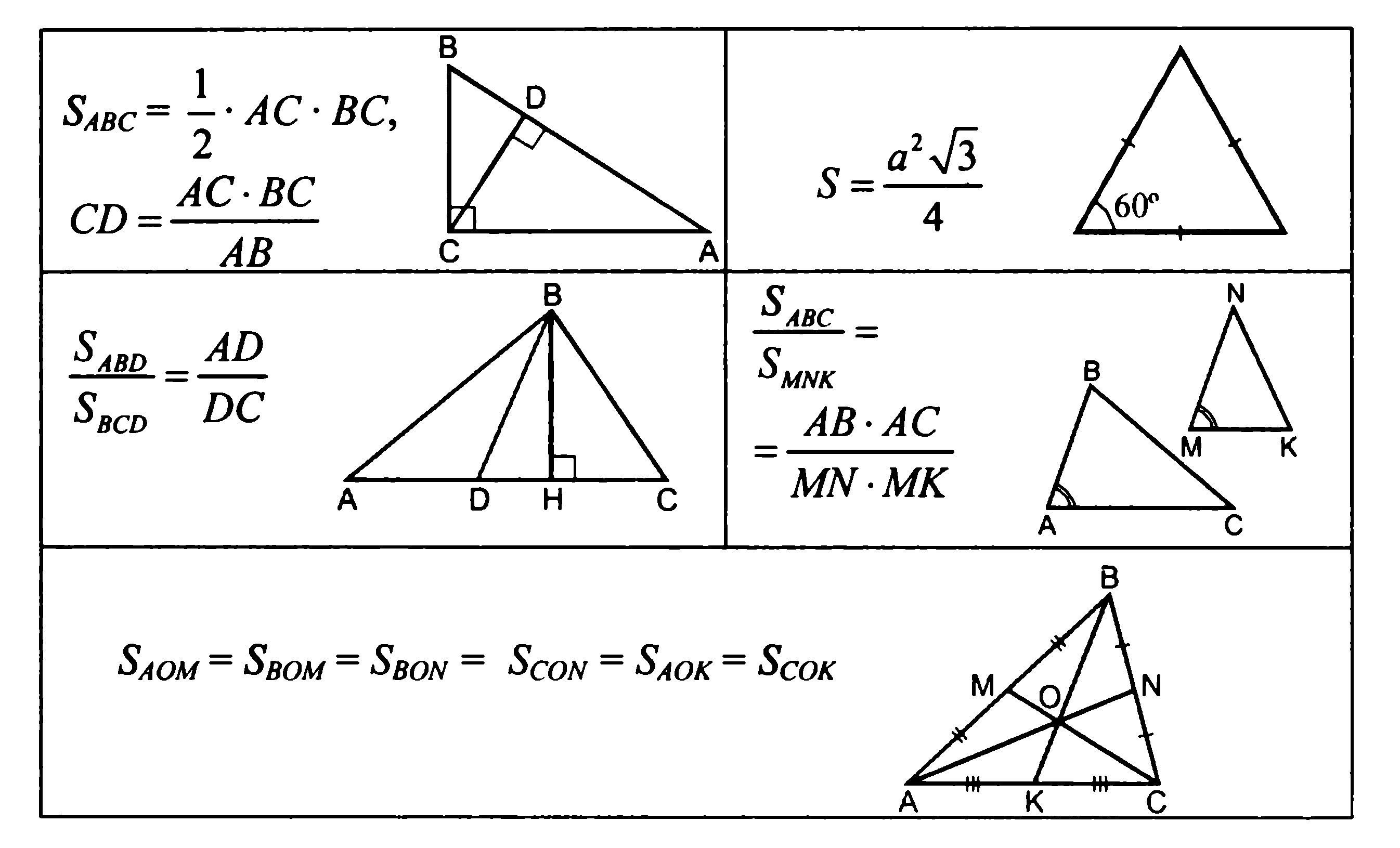
Понятие площади многоугольника. Площади прямоугольника, параллелограмма, треугольника, трапеции. Теорема Пифагора.

Основная цель: сформировать понятие площади многоугольника, развить умение вычислять площади фигур, применяя изученные свойства и формулы, применять теорему Пифагора.

В результате изучения темы учащийся должен

знать/понимать

- основные свойства площадей;

- формулу для вычисления площади прямоугольника;

- формулы для вычисления площади параллелограмма, треугольника и трапеции;

- теорему об отношении площадей треугольников, имеющих по равному углу;

- теорему Пифагора и обратную ей теорему;

уметь

- вывести формулу площади прямоугольника, параллелограмма, треугольника и трапеции;

- доказывать теорему об отношении площадей треугольников, имеющих по равному углу;

- доказывать Пифагора и обратную ей теорему;

- применять все изученные формулы при решении задач;

- выполнять чертежи по условию задачи;

использовать в практической деятельности

- конструирования новых алгоритмов;

приобретать опыт

- вычислений при осуществлении алгоритмической деятельности.

4. Подобные треугольники. (19 ч)

Основные понятия:

Подобные треугольники. Признаки подобия треугольников. Применение подобия к доказательствам теорем и решению задач. Соотношения между сторонами и углами треугольника.

Основная цель: сформировать понятия подобных треугольников, выработать умение применять признаки подобия треугольников, сформировать аппарат решения прямоугольного треугольника.

В результате изучения темы учащийся должен

знать/понимать

- понятие пропорциональных отрезков и подобных треугольников;

- теорему об отношении площадей подобных треугольников и свойство биссектрисы треугольника;

- признаки подобия треугольников;

- утверждении о пропорциональности отрезков, отсеченными параллельными прямыми на сторонах угла;

- теоремы о средней линии и пропорциональных отрезках в прямоугольном треугольнике;

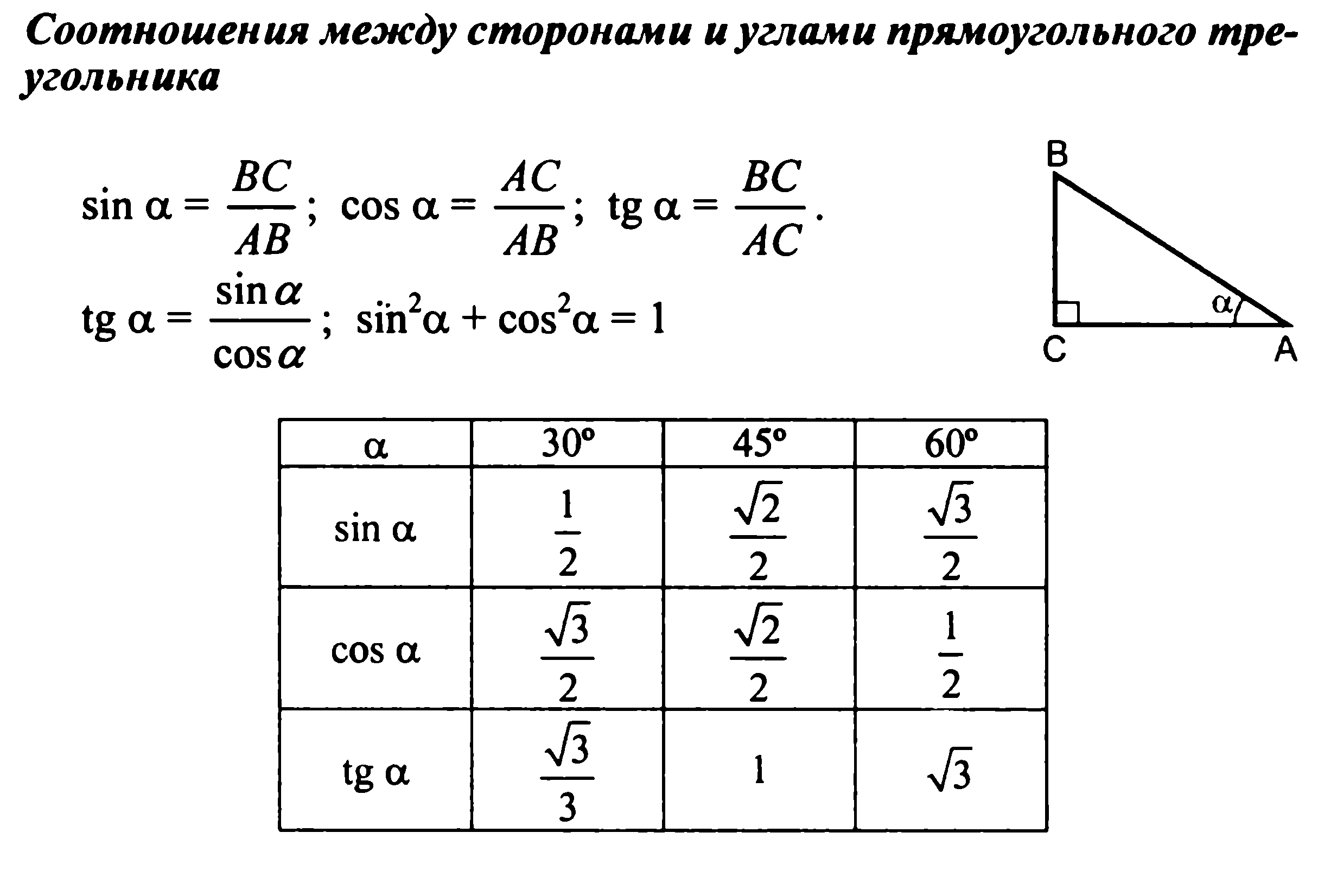
- понятие синуса, косинуса, тангенса острого угла прямоугольного треугольника;

- основное тригонометрическое тождество;

- значения синуса, косинуса, тангенса для углов 30˚, 45˚, 60˚;

уметь

- доказывать признаки подобия треугольников;

- доказывать теоремы о средней линии и пропорциональных отрезках в прямоугольном треугольнике;

- доказывать основное тригонометрическое тождество;

- выполнять чертежи по условию задачи;

- применять все изученные формулы при решении задач;

- с помощью циркуля и линейки делить отрезок в данном отношении;

- решать задачи на построение;

использовать в практической деятельности

- умения строить и исследовать простейших математических моделей;

приобретать опыт

- алгоритмической деятельности при составлении математической модели заданной ситуации.

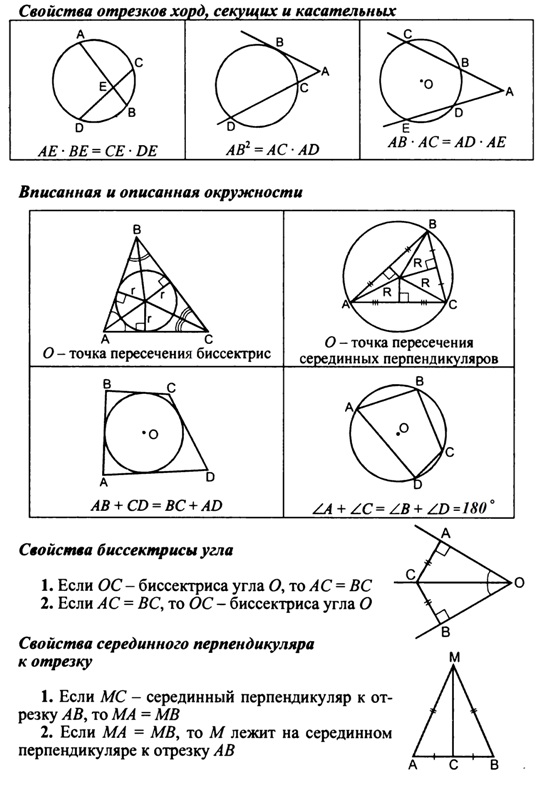
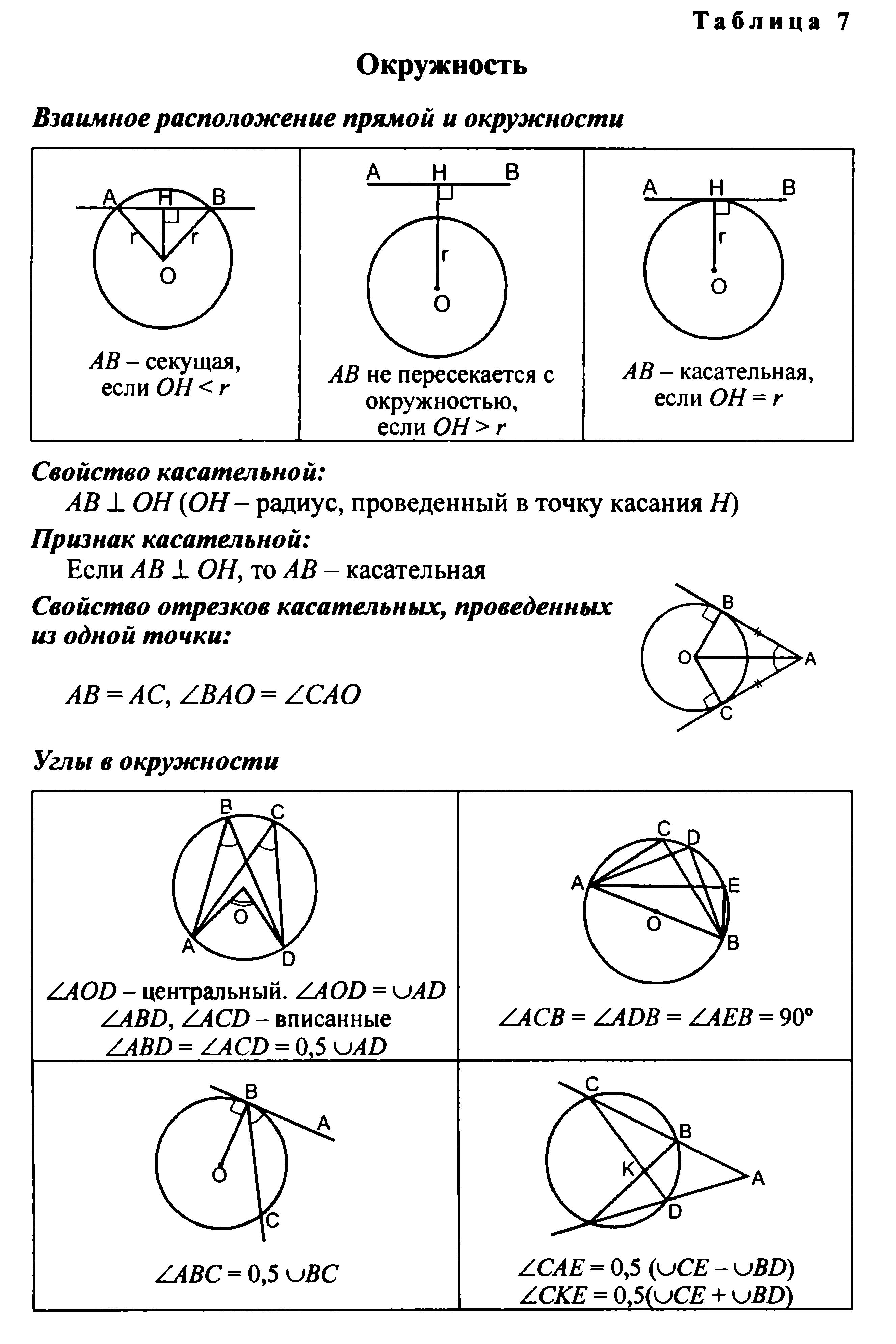
5. Окружность (16 ч)

Основные понятия: Касательная к окружности и ее свойства. Центральные и вписанные углы. Четыре замечательные точки треугольника. Вписанная и описанная окружности.

Основная цель: систематизировать сведения об окружности и ее свойствах, вписанной или описанной окружностях.

В результате изучения темы учащийся должен

знать/понимать

- возможные случаи взаимного расположения прямой и окружности;

- понятие касательной, ее свойство и признак;

- понятие центрального и вписанного угла;

- как определяется градусная мера дуги окружности;

- теорему о вписанном угле, следствия из нее;

- теорему о произведении отрезков пересекающихся хорд;

- теорему о биссектрисе угла и о серединном перпендикуляре к отрезку, их следствия;

- теорему о пересечении высот треугольника;

- понятие окружности, вписанной в многоугольник, и окружности, описанной около многоугольника;

- теорему об окружности, вписанной в многоугольник, и об окружности, описанной около многоугольника;

- свойства вписанного и описанного четырехугольника;

- при каком условии четырехугольник является вписанным и описанным;

уметь

- доказывать признак и свойства касательной;

- доказывать теорему о произведении отрезков пересекающихся хорд;

- доказывать теорему о вписанном угле, следствия из нее;

- доказывать теорему о биссектрисе угла и о серединном перпендикуляре к отрезку, их следствия;

- доказывать теорему о пересечении высот треугольника;

- доказывать теорему об окружности, вписанной в многоугольник, и об окружности, описанной около многоугольника;

- доказывать свойства вписанного и описанного четырехугольника;

- выполнять чертежи по условию задачи;

- применять все изученные теоремы и утверждения при решении задач;

- доказывать подобие треугольников с использованием соответствующих признаков;

- вычислять элементы подобных треугольников;

использовать в практической деятельности

- умения строить и исследовать простейших математических моделей;

приобретать опыт

- алгоритмической деятельности при составлении математической модели заданной ситуации.

6. Повторение. Решение задач. Резерв (5 ч)

Основные понятия: Параллелограмм и его признаки и свойства. Трапеция. Прямоугольник, ромб, квадрат и их свойства. Площади прямоугольника, параллелограмма, треугольника, трапеции. Теорема Пифагора. Признаки подобия треугольников. Применение подобия к доказательствам теорем и решению задач. Соотношения между сторонами и углами треугольника. Касательная к окружности и ее свойства. Центральные и вписанные углы. Вписанная и описанная окружности.

Основная цель: систематизация знаний учащихся

В результате изучения темы учащийся должен

знать/понимать

- формулу суммы углов выпуклого многоугольника;

- понятие и свойства равнобедренной и прямоугольной трапеции;

- понятия параллелограмма, прямоугольника, ромба и квадрата, их свойства и признаки;

- формулы для вычисления площади прямоугольника, параллелограмма, треугольника и трапеции;

- теорему об отношении площадей треугольников, имеющих по равному углу;

- теорему Пифагора;

- признаки подобия треугольников;

- теоремы о средней линии и пропорциональных отрезках в прямоугольном треугольнике;

- основное тригонометрическое тождество;

- теорему о вписанном угле, следствия из нее;

- теорему о произведении отрезков пересекающихся хорд;

- теорему об окружности, вписанной в многоугольник, и окружности, описанной около многоугольника;

- свойства вписанного и описанного четырехугольника;

уметь

- выводить и пользоваться формулой суммы углов выпуклого многоугольника;

- доказывать и применять свойства и признаки параллелограмма, трапеции, прямоугольника, ромба и квадрата при решении задач;

- выполнять чертежи по условию задачи;

- делить отрезок на n равных частей, в данном отношении с помощью циркуля и линейки;

- решать задачи на построение;

- строить симметричные точки, распознавать фигуры, обладающие осевой и центральной симметрией;

- выводить и использовать формулу площади прямоугольника, параллелограмма, треугольника и трапеции;

- применять все изученные формулы и теоремы при решении задач, проводя аргументацию в ходе решения задач;

- доказывать подобие треугольников с использованием соответствующих признаков;

- вычислять элементы подобных треугольников;

использовать в практической деятельности

- умения строить и исследовать простейших математических моделей;

-умение решать практические задачи, связанные с нахождением геометрических величин (используя при необходимости справочники и технические средства);

приобретать опыт

- алгоритмической деятельности при составлении математической модели заданной ситуации;

- вычислений при осуществлении алгоритмической деятельности.

ЛИТЕРАТУРА

Учебник: Геометрия 7-9. Авторы: Л.С.Атанасян, В.Ф.Бутузов и др. «Просвещение», Москва 2011г.

Поурочные разработки по геометрии 8 класс. Н.Ф.Гаврилова, Москва «ВАКО» 2010г.

Поурочные планы по геометрии 8 класс. Т.Л.Афанасьева, Л.А.Тапилина, изд.»Учитель»,Волгоград,2006г.

Дидактические материалы по геометрии 8 класс. Н.Б.Мельникова, Г.А.Захарова, изд. «Экзамен», Москва,2015г.

Тесты по геометрии для поурочного контроля. 8 класс. А.М.Лукашёнок, изд. «Белый ветер», 2011г.

Тематический контроль по геометрии 8 класс. Н.Б.Мельникова,Н.М.Лепихова, «Интеллект-центр»,М.2012г.

www.zavuch.info/methodlib/

math-portal.ru/

festival.1september.ru/</</font>

project.1september.ru/

Календарно - тематическое планирование составлено к учебнику «Геометрия 7-9».

Автор Л. С. Атанасян и другие.

Количество часов в неделю -2 часа

Всего за год - 70 часов

Контрольных работ - 5

Самостоятельных работ -5

«Подобные треугольники»

1

25-27.01

39-45

Работа над ошибками. Применение подобия к доказательству теорем и решению задач. См р № 4

7

28.01-19.02

46-48

Соотношения между сторонами и углами прямоугольного треугольника.

3

24.02-4.03

49

Контрольная работа № 4 по теме «Применение подобия к решению задач»

1

7.03-9.03

Окружность

17

50-52

Работа над ошибками. Касательная к окружности.

3

10-18.03

53-56

Центральные и вписанные углы.

4

21.03-8.04

57-59

Четыре замечательные точки треугольника.

3

11-19.04

60-63

Вписанная и описанная окружность. См р №5

4

20.04-6.05

64

Решение задач

1

10-12.05

65

Контрольная работа № 5 по теме «Окружность»

1

12-13.05

66

Работа над ошибками. Решение задач по теме «Четырехугольник»

1

16-18.05

67-70

Резерв

4

19-30.05

Поурочно-тематическое планирование

Наименование раздела программы

Тема и номер урока

Номер урока

Элементы содержания образования

Требования к уровню подготовки обучающихся

1

Повторение курса 7 класса

Четырехугольники.

13

Многоугольники.

2

многоугольник, элементы многоугольника, выпуклый многоугольник, сумма углов выпуклого многоугольника

-уметь строить выпуклый многоугольник;

-знать формулу суммы углов выпуклого многоугольника

Параллелограмм. Свойства параллелограмма.

3,

4

четырехугольник, параллелограмм, свойства параллелограмма

-уметь доказывать свойства параллелограмма;

-уметь решать задачи

Признаки параллелограмма.

5,

6

параллелограмм, свойства параллелограмма, признаки параллелограмма

-уметь доказывать признаки параллелограмма;

-уметь решать задачи

Трапеция.

7,

8

трапеция, элементы трапеции, равнобедренная и прямоугольная трапеция

-знать, что называют трапецией;

-уметь решать задачи на доказательство

Прямоугольник.

9,

10

прямоугольник, свойства прямоугольника, признак прямоугольника

-уметь доказывать теоремы и свойства прямоугольника;

-уметь решать задачи на их применение;

Ромб и квадрат.

11,

12

ромб, квадрат, свойство ромба и квадрата

-уметь доказывать свойства ромба и квадрата;

-уметь решать задачи

Решение задач.

13

параллелограмм, трапеция, прямоугольник, ромб, квадрат, осевая и центральная симметрии

-уметь решать задачи, опираясь на изученные свойства

Контрольная работа №1

14

-уметь применять все изученные свойства, признаки и теоремы в комплексе;

-уметь доказательно решать задачи

Площадь

14

Площадь многоугольника.

15,

16

единицы измерения площадей, площадь прямоугольника, основные свойства площадей

-уметь вывести формулу площади прямоугольника;

-уметь решать задачи на применение формулы

Площадь параллелограмма.

17,

18

параллелограмм, основание и высота параллелограмма, площадь параллелограмма

-знать формулу площади параллелограмма;

-уметь выводить формулу площади параллелограмма

Площадь треугольника.

19,

20

треугольник, основание и высота, площадь треугольника, соотношение площадей

-знать формулу площади треугольника;

-уметь находить площадь прямоугольного треугольника;

- уметь находить площадь треугольника в случае, если равны их высоты или угол

Площадь трапеции.

21,

22

трапеция, высота трапеции, площадь трапеции

-знать и уметь доказывать формулу вычисления площади трапеции;

-уметь решать задачи на применение формулы

Теорема Пифагора.

23, 24,

25

прямоугольный треугольник, теорема Пифагора, теорема, обратная теореме Пифагора

-уметь доказывать теорему Пифагора;

-уметь решать задачи на нахождение гипотенузы или катета в прямоугольном треугольнике

Решение задач.

26,

27

площадь параллелограмма, треугольника, трапеции, теорема Пифагора

-уметь находить площадь параллелограмма, треугольника, трапеции по формулам;

-уметь применять теорему Пифагора при решении задач

Контрольная работа №2.

28

-уметь применять полученные знания в комплексе

Подобные треугольники

19

Определение подобных треугольников.

29,

30

пропорциональные отрезки, сходственные стороны, подобные треугольники, коэффициент подобия, отношение площадей

-уметь определять подобные треугольники;

-уметь доказывать теорему об отношении площадей подобных треугольников

Первый признак подобия треугольников.

31,

32

подобие треугольников, первый признак подобия

-уметь доказывать первый признак подобия треугольников;

-уметь применять признак при решении задач

Второй признак подобия треугольников.

33,

34

подобие треугольников, второй признак подобия

-уметь доказывать второй признак подобия треугольников;

-уметь применять признак при решении задач

Третий признак подобия треугольников.

35

подобие треугольников, третий признак подобия

-уметь доказывать третий признак подобия треугольников;

-уметь применять признак при решении задач

Подобные треугольники

Контрольная работа №3.

36

-уметь применять первый, второй, третий признаки в комплексе при решении задач

Средняя линия треугольника.

37,

38,

39

теорема о средней линии треугольника

-уметь определять среднюю линию треугольника;

-уметь доказывать теорему о средней линии треугольника;

уметь решать задачи, используя теорему о средней линии треугольника

Пропорциональные отрезки в прямоугольном треугольнике.

40,

41

среднее пропорциональное, утверждения о среднем пропорциональном

-уметь использовать утверждения о пропорциональных отрезках в прямоугольном треугольнике при решении задач

Практические приложения подобия треугольников.

42,

43

метод подобия, построение треугольника по данным двум углам и биссектрисе при вершине третьего угла

-уметь решать задачи на построение методом подобия;

-применять подобия к доказательству теорем и решению задач

Синус, косинус и тангенс острого угла прямоугольного треугольника.

44

синус, косинус и тангенс острого угла прямоугольного треугольника, основное тригонометрическое тождество

-уметь определять синус, косинус и тангенс острого угла прямоугольного треугольника;

-знать основное тригонометрическое тождество

Значение синуса, косинуса и тангенса для углов 30⁰, 45⁰, 60⁰.

45,

46

таблица значений

-знать таблицу значений синуса, косинуса и тангенса для углов 30⁰, 45⁰, 60⁰

Контрольная работа №4.

47

-уметь применять подобия к доказательству теорем и решению задач;

-уметь решать задачи, используя соотношения между сторонами и углами прямоугольного треугольника

Окружность.

17

Взаимное расположение прямой и окружности.

48

окружность, радиус и диаметр окружности, секущая, расстояние от точки до прямой,

-знать все взаимные расположения прямой и окружности;

-уметь находить расстояние от точки до прямой

Касательная к окружности.

49,

50

касательная к окружности, точка касания

-уметь доказывать свойство и признак касательной;

-уметь определять касательную к окружности;

-уметь проводить через данную точку окружности касательную к этой окружности

-уметь решать задачи

Центральный угол.

51,

52

дуга, полуокружность, градусная мера дуги окружности, центральный угол

-уметь определять градусную меру центрального угла;

Вписанный угол.

53,

54

вписанный угол, теорема о вписанном угле

-уметь определять вписанный угол;

-доказывать теорему о вписанном угле и следствия к ней;

-знать в каком отношении пересекаются хорды окружности

Четыре замечательные точки треугольника.

55,

56,

57

свойства биссектрисы угла и серединного перпендикуляра, теорема о пересечении высот треугольника, замечательные точки треугольника

-уметь доказывать указанные теоремы;

-уметь решать задачи на применение этих теорем

Вписанная окружность.

58,

59

вписанная окружность, описанный многоугольник, теорема о вписанной окружности

-уметь вписывать окружность в многоугольник;

-уметь доказывать теорему о вписанной окружности и свойства;

Описанная окружность.

60,

61

описанная окружность, вписанный многоугольник, теорема об описанной окружности, теорема о сумме противоположных углов вписанного многоугольника

-уметь описывать окружность около многоугольника;

-уметь доказывать теорему об описанной окружности и замечания;

-знать, чему равна сумма противоположных углов вписанного многоугольника

Решение задач.

62

касательная к окружности, центральный угол, вписанный угол, замечательные точки треугольника, вписанная и описанная окружность

-уметь определять градусную меру центрального и вписанного угла;

-уметь решать задачи с использованием замечательных точек треугольника;

-знать, чему равна сумма противоположных углов вписанного многоугольника

Контрольная работа №5.

63

-уметь применять полученные знания в комплексе

Работа над ошибками. Решение задач

64

Резерв

65-

70

Образовательный минимум

Четырехугольники

Знать: определение многоугольника, формулу суммы углов выпуклого многоугольника, определение параллелограмма и его свойства, формулировки свойств и признаков параллелограмма, определение трапеции, свойства равнобедренной трапеции, формулировку теоремы Фалеса, основные типы задач на построение, определение прямоугольника, его элементы, свойства и признаки, определение ромба, квадрата как частных видов параллелограмма, виды симметрии в многоугольниках.

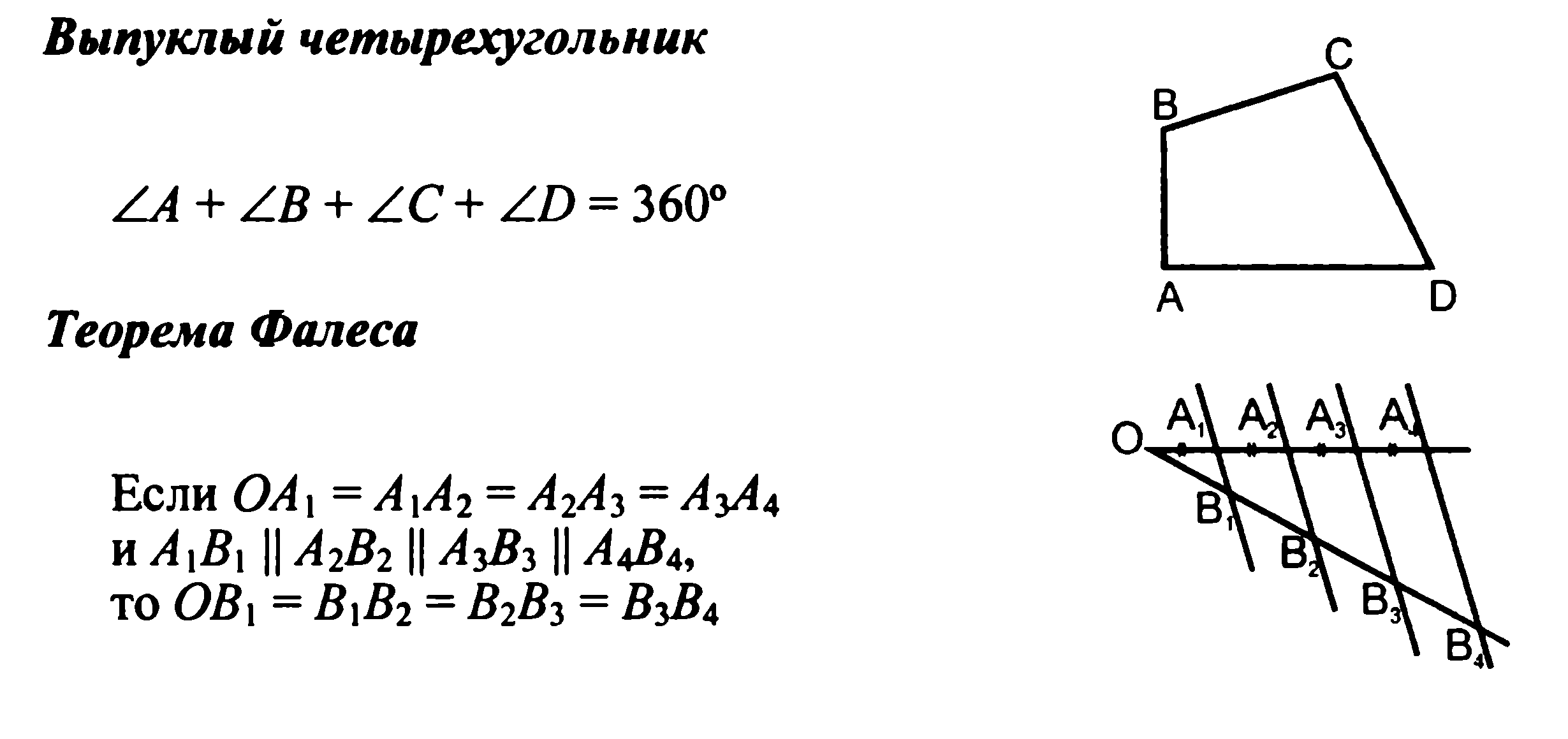
Площадь

Знать: формулу площади прямоугольника, формулу площади параллелограмма, формулу площади треугольника, формулировку теоремы об отношении площадей треугольников, формулировку теоремы о площади трапеции,

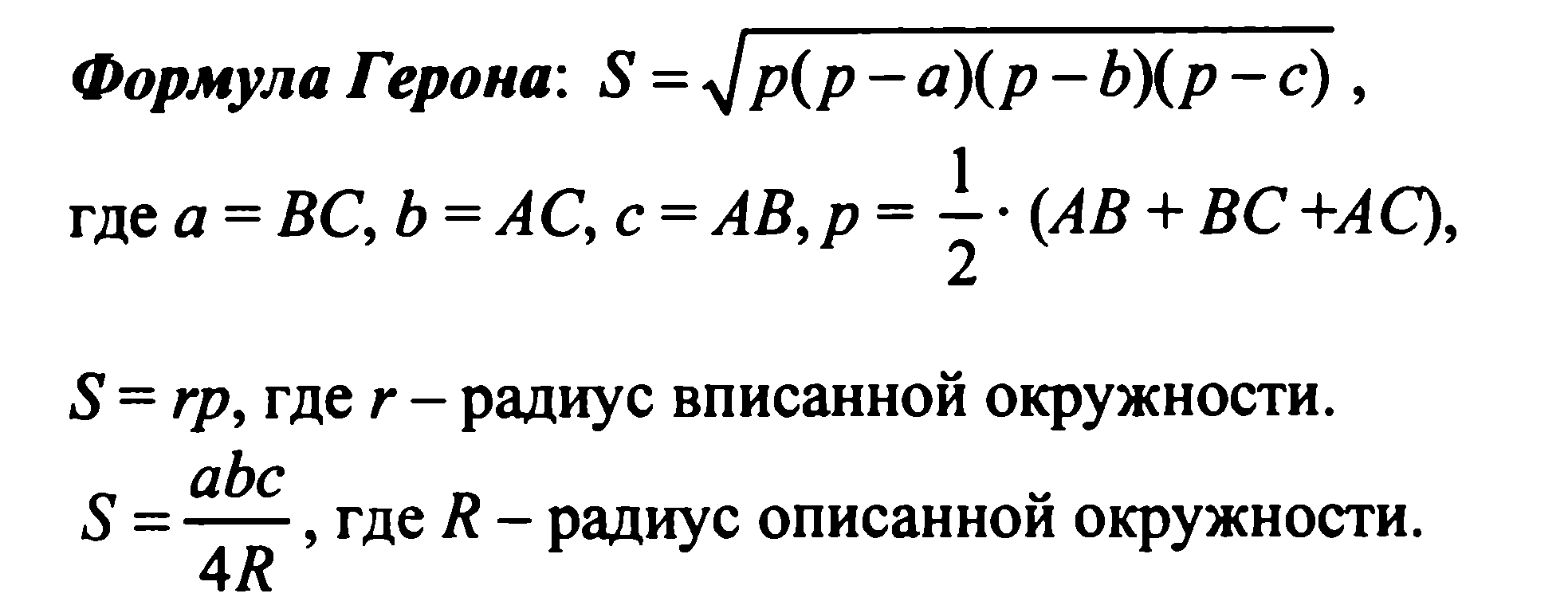
Знать: формулировку теоремы Пифагора, формулировку теоремы, обратной теореме Пифагора.

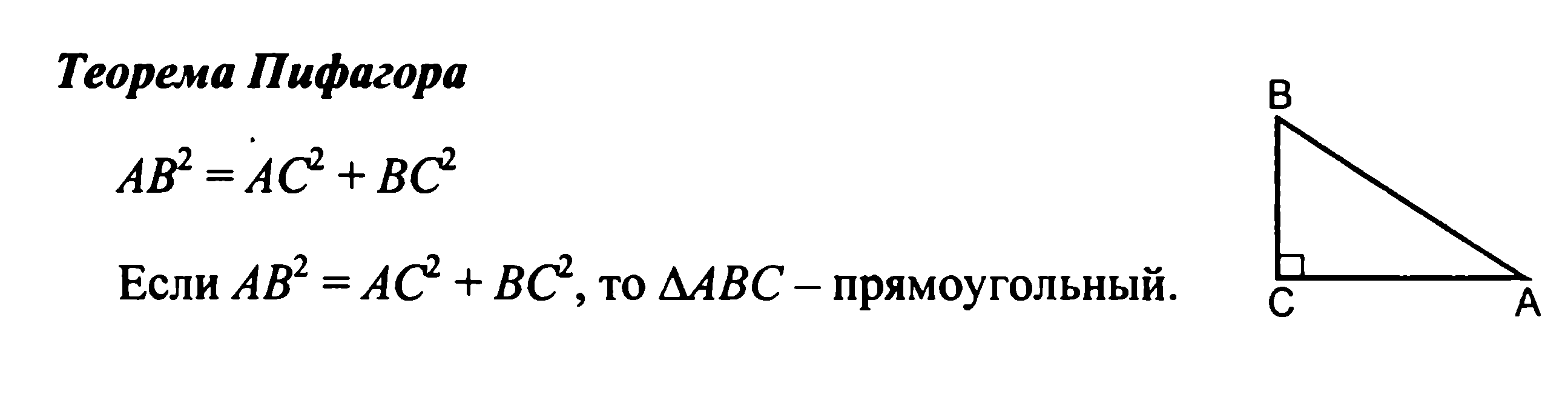Подобные треугольники

Знать: свойство биссектрисы треугольника, формулировку теоремы об отношении площадей подобных треугольников, формулировку признаков подобия треугольников.

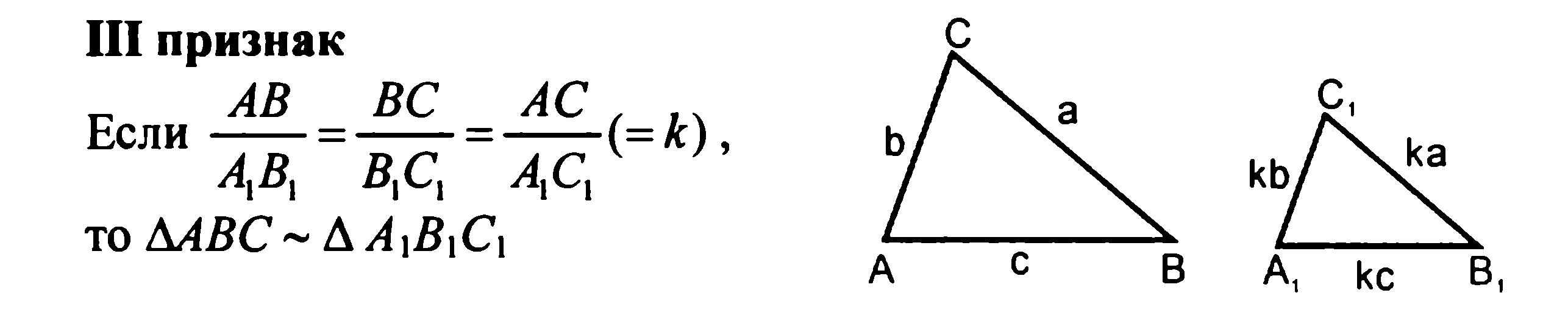
формулировку теоремы о средней линии треугольника, формулировку свойства медиан треугольника, понятие среднего пропорционального, свойство высота прямоугольного треугольника, проведенной из вершины прямого угла, теоремы о пропорциональности отрезков в прямоугольном треугольнике, понятие синуса, косинуса, тангенса острого угла прямоугольного треугольника, основное тригонометрическое тождество. значения синуса, косинуса, тангенса для углов 30⁰, 45⁰, 60⁰, 90⁰, соотношения между сторонами и углами прямоугольного треугольника.

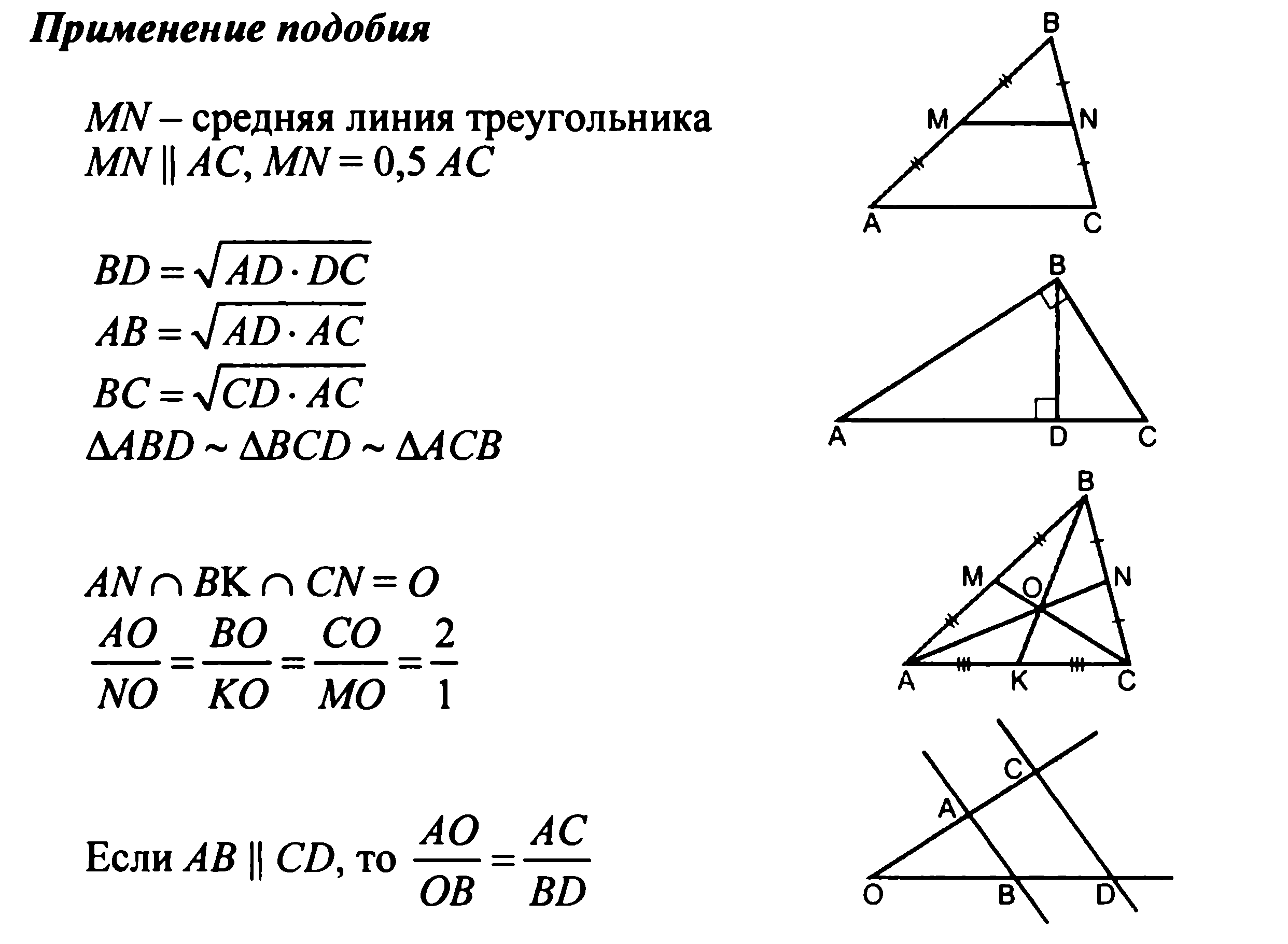
Окружность

Знать: случаи взаимного расположения прямой и окружности, понятие касательной, точек касания, свойство касательной и ее признак, взаимное расположение прямой и окружности; формулировки свойств касательной, понятие центрального угла, определение вписанного угла, теорему о вписанном угле и следствия из нее, формулировки определений вписанного и центрального углов, формулировку теоремы о свойстве равноудаленности каждой точки биссектрисы угла, понятие серединного перпендикуляра, формулировку теоремы о серединном перпендикуляре, четыре замечательные точки треугольника, формулировку теоремы о пересечении высот треугольника, понятие вписанной окружности, теорему об окружности, вписанной в треугольник, теорему о свойстве описанного четырехугольника, определение описанной окружности, формулировку теоремы об окружности, описанной около треугольника, формулировку теоремы о вписанном четырехугольнике.