Материал для подготовки к уроку по теме Пересечение и объединение множеств

УРОК 68.

Тема: Пересечение и объединение множеств.

«Множество есть многое, мыслимое нами как единое» (основатель теории множеств - Георг Кантор). КАНТОР (Cantor) Георг (1845-1918) - немецкий математик, логик, теолог, создатель теории трансфинитных (бесконечных) множеств, оказавшей определяющее влияние на развитие математических наук на рубеже 19- 20 вв.

Множество - одно из основных понятий современной математики, используемое почти во всех её разделах.

К сожалению, основному понятию теории - понятию множества - нельзя дать строгого определения. Разумеется, можно сказать, что множество - это «совокупность», «собрание», «ансамбль», «коллекция», «семейство», «система», «класс» и т. д. однако всё это было бы не математическим определением, а скорее злоупотреблением словарным богатством русского языка.

Для того чтобы определить какое - либо понятие, нужно, прежде всего, указать, частным случаем какого более общего понятия, оно является, для понятия множества сделать это невозможно, потому что более общего понятия, чем множество, в математике нет.

Часто приходится говорить о нескольких вещах, объединенных некоторым признаком. Так, можно говорить о множестве всех стульев в комнате, о множестве всех клеток человеческого тела, о множестве всех картофелин в данном мешке, о множестве всех рыб в океане, о множестве всех квадратов на плоскости, о множестве всех точек на данной окружности т. д.

Предметы, составляющие данное множество, называются его элементами.

Например, множество дней недели состоит из элементов: понедельник, вторник, среда, четверг, пятница, суббота, воскресенье.

Множество месяцев - из элементов: январь, февраль, март, апрель, май, июнь, июль, август, сентябрь, октябрь, ноябрь, декабрь.

Множество арифметических действий - из элементов: сложение, вычитание, умножение, деление.

Например, если А означает множество всех натуральных чисел, то 6 принадлежит к А, а 3 не принадлежит к А.

Если А - множество всех месяцев в году, то май принадлежит к А, а среда не принадлежит к А.

Если множество содержит конечное число элементов, то его называют конечным, а если в нем бесконечно много элементов, то бесконечным. Так множество деревьев в лесу конечно, а множество точек на окружности бесконечно.

Парадокс в логике - это противоречие, имеющее статус логически корректного вывода и, вместе с тем, представляющее собой рассуждение, приводящее к взаимно исключающим заключениям.

Как уже упоминалось, понятие множества лежит в основе математики. Используя простейшие множества и различные математические конструкции, можно построить практически любой математический объект. Идею построения всей математики на основе теории множеств активно пропагандировал Г.Кантор. Однако, при всей своей простоте, понятие множества таит в себе опасность появления противоречий или, как ещё говорят, парадоксов. Появление парадоксов связано с тем, что далеко не всякие конструкции и не всякие множества можно рассматривать.

Самый простой из парадоксов - это "парадокс брадобрея".

Одному солдату было приказано брить тех и только тех солдат его взвода, которые сами себя не бреют. Неисполнение приказа в армии, как известно, тягчайшее преступление. Однако возник вопрос, брить ли этому солдату самого себя. Если он побреется, то его следует отнести к множеству солдат, которые сами себя бреют, а таких брить он не имеет права. Если же он себя брить не будет, то попадёт во множество солдат, которые сами себя не бреют, а таких солдат согласно приказу он обязан брить. Парадокс.

Над множествами, как и над многими другими математическими объектами, можно совершать различные операции, которые иногда называют теоретико-множественными операциями или сет-операциями. В результате операций из исходных множеств получаются новые. Множества обозначаются заглавными латинскими буквами, а их элементы - строчными. Запись aR означает, что элемент а принадлежит множеству R , то есть а является элементом множества R . В противном случае, когда а не принадлежит множеству R , пишут aR .

Два множества А и В называются равными ( А = В ), если они состоят из одних и тех же элементов, то есть каждый элемент множества А является элементом множества В и наоборот, каждый элемент множества В является элементом множества А .

Сравнение множеств.

Множество A содержится во множестве B (множество B включает множество A), если каждый элемент A есть элемент В:

Говорят, что множество А содержится в множестве В или множество Аявляется подмножеством множества В ( в этом случае пишут А В ), если каждый элемент множества А одновременно является элементом множества В . Эта зависимость между множествами называется включением. Для любого множества А имеют место включения: ØА и А А

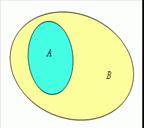
В этом случае A называется подмножеством B, B - надмножеством A. Если , то A называется собственным подмножеством В. Заметим, что ,

По определению ,

Два множества называются равными, если они являются подмножествами друг друга

Операции над множествами

Пересечение.

Объединение.

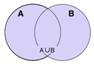
Свойства.

1.Операция объединения множеств коммутативна

2.Операция объединения множеств транзитивна

3. Пустое множество X является нейтральным элементом операции объединения множеств

Примеры:

1. Пусть A = {1,2,3,4},B = {3,4,5,6,7}. Тогда

2. А={2,4,6,8,10}, В = {3,6,9,12}. Найдём объединение и пересечение этих множеств:

{2,4,6,8, 10,3,6,9,12}, = {6}.

3. Множество детей является подмножеством всего населения

4. Пересечением множества целых чисел с множеством положительных чисел является множество натуральных чисел.

5. Объединением множества рациональных чисел с множеством иррациональных чисел является множество положительных чисел.

6.Нуль является дополнением множества натуральных чисел относительно множества неотрицательных целых чисел.

Диаграммы Венна (Venn diagrams) - общее название целого ряда методов визуализации и способов графической иллюстрации, широко используемых в различных областях науки и математики</<font face="Times New Roman, serif">: теория множеств, собственно «диаграмма Венна» показывает все возможные отношения между множествами или событиями из некоторого семейства; разновидностями диаграмм Венна служат: диаграммы Эйлера,

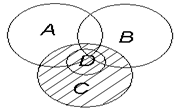
Диаграмма Венна четырёх множеств.

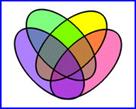
Собственно «диаграмма Венна» показывает все возможные отношения между множествами или событиями из некоторого семейства. Обычная диаграмма Венна имеет три множества. Сам Венн пытался найти изящный способ с симметричными фигурами, представляющий на диаграмме большее число множеств, но он смог это сделать только для четырех множеств (см. рисунок справа), используя эллипсы.

Диаграммы Эйлера

Диаграммы Эйлера аналогичны диаграммам Венна.Диаграммы Эйлера можно использовать, для того, чтобы оценивать правдоподобность теоретико-множественных тождеств.

Задача 1. В классе 30 человек, каждый из которых поёт или танцует. Известно, что поют 17 человек, а танцевать умеют 19 человек. Сколько человек поёт и танцует одновременно?

Решение: Сначала заметим, что из 30 человек не умеют петь 30 - 17 = 13 человек.

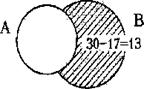
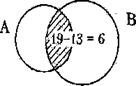
Все они умеют танцевать, т.к. по условию каждый ученик класса поёт или танцует. Всего умеют танцевать 19 человек, из них 13 не умеют петь, значит, танцевать и петь одновременно умеют 19-13 = 6 человек.

Задачи на пересечение и объединение множеств.

1. Даны множества А = {3,5, 0, 11, 12, 19}, В = {2,4, 8, 12, 18,0}.
   
   Найдите множества AU В,

2. Составьте не менее семи слов, буквы которых образуют подмножества множества
   
   А -{к,а,р,у,с,е,л,ь}.

3. Пусть A - это множество натуральных чисел, делящихся на 2, а В - множество натуральных чисел, делящихся на 4. Какой вывод можно сделать относительно данных множеств?

4. На фирме работают 67 человек. Из них 47 знают английский язык, 35 - немецкий язык, а 23 - оба языка. Сколько человек фирмы не знают ни английского, ни немецкого языков?

5. Из 40 учащихся нашего класса 32 любят молоко, 21 - лимонад, а 15 - и молоко, и лимонад. Сколько ребят в нашем классе не любят ни молоко, ни лимонад?

6. 12 моих одноклассников любят читать детективы, 18 -фантастику, трое с удовольствием читают и то, и другое, а один вообще ничего не читает. Сколько учеников в нашем классе?

7. Из тех 18 моих одноклассников, которые любят смотреть триллеры, только 12 не прочь посмотреть и мультфильмы. Сколько моих одноклассников смотрят одни «мультики», если всего в нашем классе 25 учеников, каждый из которых любит смотреть или триллеры, или мультфильмы, или и то и другое?

8. Из 29 мальчишек нашего двора только двое не занимаются спортом, а остальные посещают футбольную или теннисную секции, а то и обе. Футболом занимается 17 мальчишек, а теннисом - 19. Сколько футболистов играет в теннис? Сколько теннисистов играет в футбол?

9. 65 % бабушкиных кроликов любят морковку, 10 % любят и морковку, и капусту. Сколько процентов кроликов не прочь полакомиться капустой?

10. В одном классе 25 учеников. Из них 7 любят груши, 11 -черешню. Двое любят груши и черешню; 6 - груши и яблоки; 5 -яблоки и черешню. Но есть в классе два ученика, которые любят все и четверо таких, что не любят фруктов вообще. Сколько учеников этого класса любят яблоки?

11. В конкурсе красоты участвовали 22 девушки. Из них 10 было красивых, 12 -умных и 9 -добрых. Только 2 девушки были и красивыми, и умными; 6 девушек были умными и одновременно добрыми. Определите, сколько было красивых и в то же время добрых девушек, если я скажу вам, что среди участниц не оказалось ни одной умной, доброй и вместе с тем красивой девушки?

12. В нашем классе 35 учеников. За первую четверть пятерки по русскому языку имели 14 учеников; по математике - 12; по истории - 23. По русскому и математике - 4; по математике и истории - 9; по русскому языку и истории - 5. Сколько учеников имеют пятерки по всем трем предметам, если в классе нет ни одного ученика, не имеющего пятерки хотя бы по одному из этих предметов?

13. Из 100 человек 85 знают английский язык, 80 - испанский, 75 - немецкий. Все владеют, по крайней мере, одним иностранным языком. Среди них нет таких, которые знают два иностранных языка, но есть владеющие тремя языками. Сколько человек из этих 100 знают три языка?

14. Из сотрудников фирмы 16 побывали во Франции, 10 -в Италии, 6 - в Англии; в Англии и Италии - 5; в Англии и Франции - 6; во всех трех странах - 5 сотрудников. Сколько человек посетили и Италию, и Францию, если всего в фирме работают 19 человек, и каждый из них побывал хотя бы в одной из названных стран?