Решение задач по теме 'Пирамида' координатным методом

Муниципальное бюджетное общеобразовательное учреждение средняя общеобразовательная школа с углубленным изучением отдельных предметов №68, г. Липецка

ТЕМА УРОКА:

Решение задач по теме «Пирамида » координатным методом

(11 класс)

Учитель: Щукина О.А.

Липецк 2013

Цель урока:

Способствовать развитию навыка решения задач координатным методом на примере решения задач по теме «Пирамида» типа С2 ЕГЭ.

Задачи:

1. систематизировать знания учащихся;

2. совершенствовать навыки решения задач методом координат;

3. способствовать развитию внимательности, воображения;

4. способствовать воспитанию самостоятельности, активности.

Ход урока

1. Мотивация (самоопределение) к учебной деятельности (2мин)
   «Я хочу»
   Ребята, вы хотите хорошо сдать ЕГЭ по математике?
   Хотите научиться решать задачи по геометрии?

Если да, то многое будет зависеть от вас. Вы должны переключить все свое внимание на урок, убрать лишние вещи, на время забыть жизненные проблемы.

Три пути ведут к знанию:

Путь размышления - это путь самый благородный,

Путь подражания - это путь самый легкий,

И путь опыта - это путь самый горький.

(Конфуций)

«Я могу»

Эти три пути нам предстоит пройти сегодня на уроке. Если вам что-то не будет понятно, обращайтесь к учителю. Проблемы, которые вы будете решать на уроке, вполне преодолимы, нужно всего лишь сделать небольшое усилие, напрячь мозги.

2. Актуализация знаний и фиксация индивидуального затруднения в пробном действии (5 минут).

Путь подражания - это путь самый легкий

Задание 1: Продолжи предложение, вставив недостающие слова. Основные определения стереометрии:

Ненулевой вектор называется направляющим вектором прямой a, если он лежит либо на прямой a , либо на прямой, параллельной a.

Угол между векторами - это угол между векторами, равными данным и отложенными от одной точки.

Углом между прямыми в пространстве будем называть острый из вертикальных углов, образованных двумя прямыми, проведёнными через произвольную точку параллельно данным.

Угол между прямой и плоскостью это угол между прямой и ее проекцией на эту плоскость.

Угол между плоскостями - это угол между перпендикулярами к линии их пересечения, проведенными в этих плоскостях.

Отрезок, имеющий концы на двух скрещивающихся прямых и перпендикулярный к ним, называется общим перпендикуляром скрещивающихся прямых.

Расстояние между скрещивающимися прямыми равно длине общего перпендикуляра скрещивающихся прямых.

Расстояние от точки до прямой - длина перпендикуляра, опущенного из точки на прямую.

Расстояние от точки до плоскости- длина перпендикуляра, опущенного из точки на плоскость.

Расстояние между параллельными прямой и плоскостью длина перпендикуляра, опущенного из любой точки прямой на плоскость.

Расстояние между параллельными прямыми (плоскостями)- длина перпендикуляра, опущенного из любой точки одной прямой (плоскости) на другую прямую (плоскость).

Нормальный вектор плоскости это любой ненулевой вектор, лежащий на любой прямой перпендикулярной к данной плоскости.

Общее уравнение плоскости, где {А;В;С} - вектор нормали Ах+Ву+Сz+D = 0

Общее уравнение плоскости, проходящей через точку М (х₀; у₀;z₀) и вектор нормали {А;В;С} - вектор нормали

А(х - х₀ )+В( у- у₀ )+С (z - z₀ ) = 0

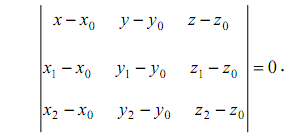
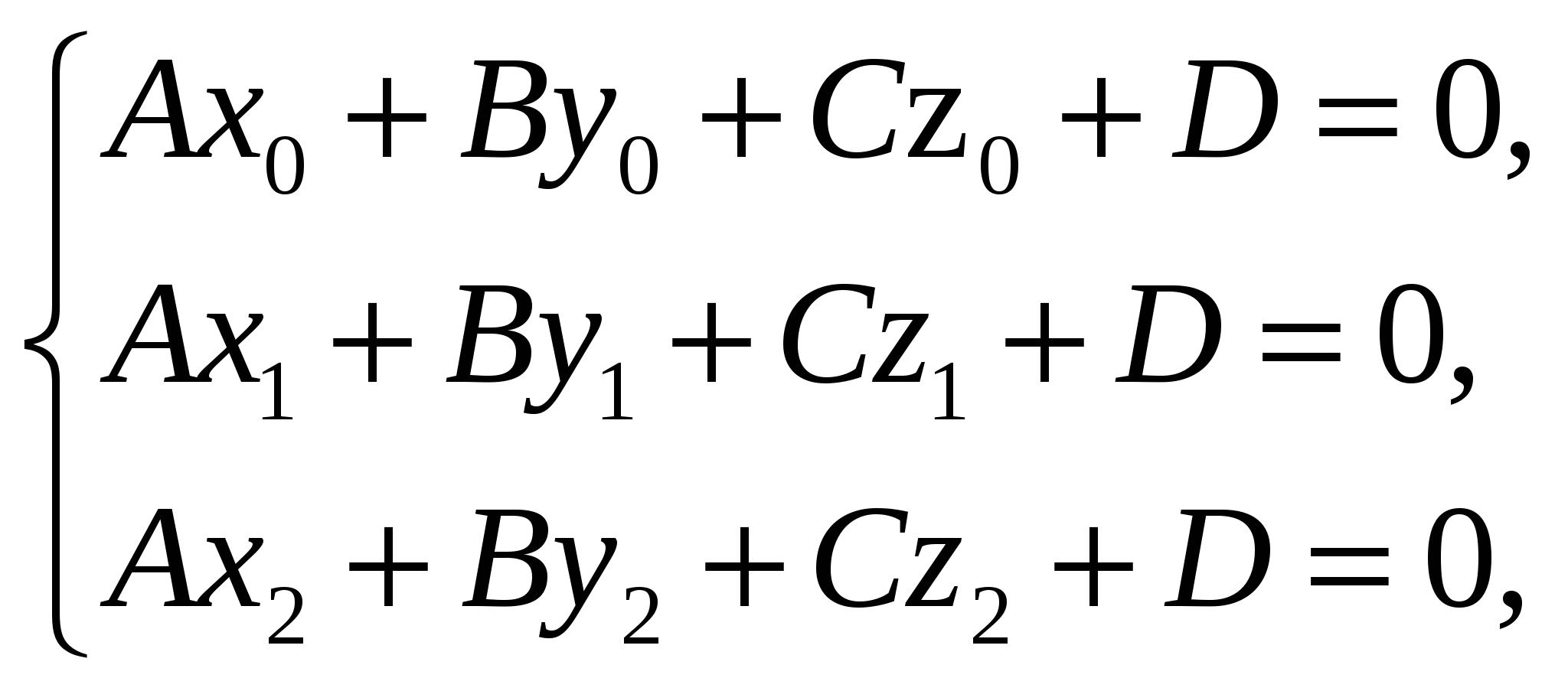
3. Выявление места и причины затруднения (2 минуты)

Задание : Угадай формулу

Тему урока учащиеся формулирую самостоятельно, отвечая на вопрос « Для чего мы сегодня повторяли данные формулы?»

ТЕМА урока: Решение задач по теме «Пирамида » координатным методом.

4. Построение проекта выхода из затруднения(5 мин)

Постановка цели:

В чем заключается цель нашей дальнейшей работы?(применение метода координат в решении задач по «Пирамида»)

Что необходимо знать для решения задач данным методом? (основной алгоритм решения задач координатным методом)

Что для ВАС самое сложное в данном алгоритме? (выбрать систему координат и определить координаты необходимых точек)

Мозговой штурм.

Задание: Найди ошибку.

Каждая группа из 3-4 учащихся разрабатывает план решения с проговариванием решения вслух.

Выслушиваются все мнения.
Отмечаем плюсы и минусы каждого решения(Принцип вариативности) и сравниваем с решением, который приведен на слайде.

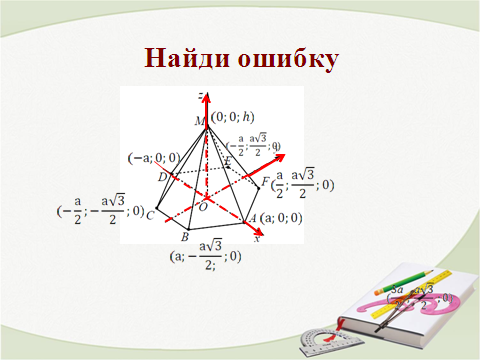
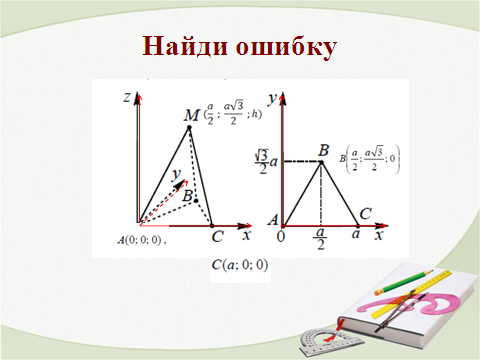
Физкультминутка для глаз (3 минуты)

5. Реализация построенного проекта, самостоятельное решение задач по группам (задачи дифференцированы по сложности) (15 мин)

Путь размышления - это путь самый благородный,

1 группа: : В правильной шестиугольной пирамиде SАВСDEF, стороны основания равны 1, а боковые ребра равны 2, точка К - середина ребра SF. Найдите градусную меру угла между прямой ВК плоскостью основания.

2 группа:

В правильной четырехугольной пирамиде FABCD сторона квадрата АВСD, лежащего в основании, равна , а высота, опущенная на основание, равна 2. Найдите расстояние от вершины А до плоскости DFС.

3 группа:

Сторона основания АВС правильной треугольной пирамиды DАВС равна , а боковое ребро 5. Найдите объем пирамиды DАРК, где Р и К - середины ребер DВ и DС.

6. Проверка, решенных задач( 10мин.)

И путь опыта - это путь самый горький.

7. Итог урока. Рефлексия - 5 мин.

- Подведем итог урока. Какова была цель урока?

- Как вы считаете, достигнута ли она?

- Удовлетворены ли вы работой своей группы?

-Считаете ли вы, что в вашей группе преобладала атмосфера взаимопонимания и взаимного уважения?

- Считаете ли вы свою работу на уроке полезной для вашей группы?

- Можете ли вы оценить работу вашей группы как способствующую достижению цели урока?

- Можете ли вы сказать, что в ходе урока произошло обогащение запаса ваших знаний?

- Какое открытие для себя вы сделали?

Вы систематизировали теоретические знания по методу координат, применили свои знания при решении нестандартных задач, готовились к ГИА.

СПАСИБО ЗА УРОК!

Домашнее задание: решить данные задачи геометрическим методом.