- Учителю
- Разработка урока внеурочной деятельности Магические квадраты
Разработка урока внеурочной деятельности Магические квадраты
Урок № 19-21
Логика 5 класс
Тема: «Знакомство с магическими квадратами. Магические квадраты»
Цель:
-
знакомство с магическими квадратами - что это такое;
-
виды магических квадратов и их решение;
-
познакомить ребят с правилами составления магических квадратов;
-
научить их придумывать такие квадраты;
-
способствовать развитию умений анализировать, сравнивать, обобщать, выделять главное; развивать осознанную математическую речь; развитие познавательного интереса учащихся;
-
содействовать воспитанию таких качеств как: самостоятельность, целеустремленность, настойчивость, целенаправленность, трудолюбие, аккуратность, ответственность
Задачи:
- Продолжить формирование навыков контроля результатов деятельности.
- Способствовать развитию коммуникативных навыков. Развивать умение анализировать, обобщать материал, выступать перед аудиторией, развивать интеллектуальные, творческие и исследовательские способности, активизировать интерес к учебным предметам.
- Формирование логического, абстрактного, эвристического, системного мышления.
Оборудование: проектор, экран, компьютер, презентации
План.
-
Организационные моменты
-
Что такое магический квадрат.
В давние времена, научившись считать и выполнять арифметические действия, люди с удивление обнаружили, что числа имеют самостоятельную жизнь, удивительную и таинственную. Складывая различные числа, располагая их друг за другом или одно под другим, они иногда получали одинаковую сумму. Наконец, разделив числа линиями так, чтобы каждое оказалось в отдельной клетке, увидели квадрат, любое из чисел которого принимало участие в двух суммах, а те, что расположены вдоль диагоналей - даже в трех, и все суммы равны между собой! Недаром древние китайцы, индусы, а вслед за ними и арабы приписывали таким конструкциям таинственные и магические свойства. (слайд 1)
Магические квадраты появились на Древнем Востоке еще до нашей эры. Одна из сохранившихся легенд повествует о том, что когда император Ю из династии Шан (2000 г до н.э.) стоял на берегу Ло, притоке Желтой реки, вдруг появилась большая рыба (в других вариантах - огромная черепаха), у которой на спине был рисунок из двух мистических символов - черных и белых кружочков (слайд 2), который был осознан затем как изображение магического квадрата порядка 3. (слайд 3)
Первое специальное упоминание о таком квадрате найдено около 1 века до н.э. Вплоть до 10 века н.э. магические квадраты были воплощены в амулетах, заклинаниях. Они использовались в качестве талисманов по всей Индии. Их рисовали на кувшинах удачи, медицинских кружках. До сих пор они используются у некоторых восточных народов как талисман. Их можно встретить на палубах больших пассажирских судов как площадку для игры.
Итак, под магическими будем понимать квадраты, в которых суммы чисел, стоящих в любом столбце или в любой строке, а также по диагоналям, одинаковы.
До сих пор вы использовали магические квадраты чаще всего для устного счета. При этом несколько чисел, в том числе и центральное, уже расставлены по клеткам квадрата. Требуется расставить остальные числа так, чтобы в любом направлении получилась определенная сумма.
-
Решение задач на магические квадраты
Построение магических квадратов
Метод террас
Описан Ю. В. Чебраковым в «Теории магических матриц».
Для заданного нечетного n начертим квадратную таблицу размером n на n. Пристроим к этой таблице со всех четырех сторон террасы (пирамидки). В результате получим ступенчатую симметричную фигуру.
5
3
4
10
2
3
9
15
1
2
8
14
20
0
1
7
13
19
25
-1
6
12
18
24
-2
11
17
23
-3
16
22
-4
21
.
-4
-3
-2
-1
0
1
2
3
4
Начиная с левой вершины ступенчатой фигуры, заполним ее
диагональные ряды последовательными натуральными числами от 1 до
.
После этого для получения классической матрицы N-го порядка числа, находящиеся в террасах, поставим на те места таблицы размером NxN, в которых они оказались бы, если перемещать их вместе с террасами до того момента, пока основания террас не примкнут к противоположной стороне таблицы.
3
2
3
16
9
22
15
1
20
8
21
14
2
0
7
25
13
1
19
-1
24
12
5
18
6
-2
11
4
17
10
23
-3
-4
.
-4
-3
-2
-1
0
1
2
3
4
16
9
22
15
20
8
21
14
2
7
25
13
1
19
24
12
5
18
6
11
4
17
10
23
Прочие способы
Правила построения магических квадратов делятся на три категории
в зависимости от того, каков порядок квадрата: нечетен, равен
удвоенному нечетному числу или равен учетверенному нечетному числу.
Общий метод построения всех квадратов неизвестен, хотя широко
применяются различные схемы. Найти все магические квадраты порядка
удается только для 
,
поэтому представляют большой интерес частные процедуры построения
магических квадратов при 
.
Проще всего конструкция для магического квадрата нечетного порядка.
Нужно в клетку с координатами 
поставить число
Ещё проще построение выполнить следующим образом. Берётся матрица n x n . Внутри её строится ступенчатый ромб. В нём ячейки слева вверх по диагоналям заполняются последовательным рядом нечётных чисел. Определяется значение центральной ячейки C. Тогда в углах магического квадрата значения будут такими: верхняя правая ячейка C-1 ; нижня левая ячейка C+1 ; нижняя правая ячейка C-n; верхняя левая ячейка C+n. Заполнение пустых ячеек в ступенчатых угловых треугольниках ведётся с соблюдением простых правил: 1)по строкам числа слева направо увеличиваются с шагом n + 1; 2) по столбцам сверху вниз числа увеличиваются с шагом n-1.
Также разработаны алгоритмы построения пандиагональных
квадратов, и идеальных магических квадратов 9x9. Эти результаты
позволяют строить идеальные магические квадраты порядков 
для
.
Существуют также общие методы компоновки идеальных магических
квадратов нечётного порядка 
.
Разработаны методы построения идеальных магических квадратов
порядка n=8k, k=1,2,3… и совершенных магических квадратов.
Пандиагональные и идеальные квадраты четно-нечётного порядка
удаётся скомпоновать лишь в том случае, если они нетрадиционные.
Тем не менее, можно находить почти пандиагональные квадраты.
Найдена особая группа идеально-совершенных магических квадратов
(традиционных и нетрадиционных).
Примеры более сложных квадратов
Методически строго отработаны магические квадраты нечётного порядка и порядка двойной чётности. Формализация квадратов порядка одинарной чётности намного труднее, что иллюстрируют следующие схемы:
24
5
6
12
22
3
9
15
16
1
7
13
19
25
10
11
17
23
4
14
20
21
2
8
2
3
61
60
6
7
57
9
55
54
12
13
51
50
16
17
47
46
20
21
43
42
24
40
26
27
37
36
30
31
33
32
34
35
29
28
38
39
25
41
23
22
44
45
19
18
48
49
15
14
52
53
11
10
56
8
58
59
5
4
62
63
1
99
93
7
5
6
4
8
92
91
11
89
88
84
16
15
17
83
82
20
30
22
78
77
75
26
74
73
29
21
61
39
33
67
66
65
64
38
32
40
60
52
48
44
56
55
47
43
49
51
50
42
53
54
46
45
57
58
59
41
31
62
63
37
36
35
34
68
69
70
71
72
28
27
25
76
24
23
79
80
81
19
18
14
85
86
87
13
12
90
10
9
3
94
95
96
97
98
2
1
Существуют несколько десятков других методов построения магических квадратов
Шахматный подход
Известно, что шахматы, как и магические квадраты, появились десятки веков назад в Индии. Поэтому неслучайно возникла идея шахматного подхода к построению магических квадратов. Впервые эту мысль высказал Эйлер. Он попытался получить полный магический квадрат непрерывным обходом коня. Однако, это сделать ему не удалось, поскольку в главных диагоналях суммы чисел отличались от магической константы. Тем не менее шахматная разбивка позволяет создавать любой магический квадрат. Цифры заполняются регулярно и построчно с учётом цвета ячеек.
Задачи на построение магических квадратов
Задача 1. Даны числа 1, 2, 3, 4, 5, 6, 7, 8, 9. Часть из них расставлена по клеткам Требуется расставить остальные числа, чтобы в сумме получалось 15. (слайд 4)
Можно заметить ряд закономерностей, облегчающих заполнение клеток квадрата или дающих возможность решить задачу при меньшем числе данных в условии.
Например, в условиях задач, подобных предыдущей, не обязательно указывать, какая сумма должна получиться в любом направлении.
Задача 2. Найдите способ, как сосчитать сумму по строчкам, столбцам и диагоналям из предыдущей задачи.
Можно рассуждать следующим образом: сумма чисел в каждой строке одинакова, таких строк 3, значит сумма чисел в каждой строке в три раза меньше суммы всех чисел. Следовательно, в нашем примере, сумма в каждой строке равна 15 (45 : 3). Но это число можно найти и другими способами: сложить три центральных числа 4, 5 и 6 или умножить центральное число 5 на 3.
Задача 3. Даны числа: 2, 3, 4, 5, 6, 7, 8, 9, 10. Требуется вписать их в клетки квадрата так, чтобы в любом направлении в сумме получилось одно и то же число. Часть чисел уже вписана в квадрат. (слайд 7)
Получаем следующий квадрат: (слайд 8)
Посмотрите, какое число стоит в центре квадрата? Как оно расположено в ряду данных чисел? (слайд 12) (В центре квадрата всегда записывается число, стоящее на пятом месте нашей последовательности, т. е. одинаково удаленное с левого и правого ее краев.)
Можно заметить еще ряд особенностей: в квадрате по разные стороны от центрального числа стоят числа, одинаково удаленные от левого и правого краев последовательности. Покажем пары соответствующих чисел на примере заполнения квадрата числами от 1 до 9: (слайд 13)
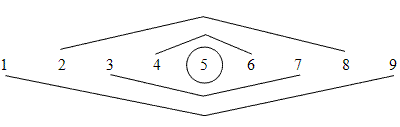
Зная это, можно заполнить квадрат, почти не считая.
Посмотрите, как расположены в квадрате числа, стоящие рядом с центральным, а также числа, записанные от них через одно число. Они соединены линиями сверху. (Они расположены по диагоналям квадрата.) А где расположены остальные числа, которые соединены линиями снизу? (Они расположены по вертикали и по горизонтали.)
Давайте проверим, выполняются ли такие закономерности в других квадратах. (слайд 14)
(Да, такие закономерности выполняются.)
Итак, давайте подведем итог. Какие свойства магических квадратов мы выяснили?
1) Чтобы найти сумму чисел в каждом столбце или строке, можно центральное число умножить на 3.
2) В центре квадрата стоит число, записанное в ряду пятым.
3) В квадрате по разные стороны от центрального числа стоят числа, одинаково удаленные от левого и правого краев последовательности.
4) Числа, стоящие рядом с центральным и через одно от него, расположены по диагоналям квадрата. Числа, стоящие с краю и через одно от него, расположены в квадрате по вертикали и по горизонтали.
Задача 5. Даны числа: 3, 4, 5, 6, 7, 8, 9, 10, 11. Впишите их в клетки квадрата так, чтобы в любом направлении получилось одно и то же число. (слайд 15)
(Найдем, какая сумма должна получаться в каждом направлении. Для этого умножим центральное число 7 на 3. В результате получим 21. В центр квадрата поставим число 7, по одной диагонали числа 6 и 8, по другой - 4 и 10. Осталось расставить недостающие числа: сумма записанных в первой строке чисел равна 10, до 21 недостает 11, значит, в пустой клетке верхней строки запишем число 11 (первое справа). Тогда в нижней строке запишем число 3 (первое слева). В левый столбик запишем число 5 (21 - (6 + 10)), тогда в правом столбике останется записать число 9. Таким образом, мы расставили все 9 чисел в клетки магического квадрата, при этом ни одно число по условию задачи в квадрате не было поставлено.)
Задача имеет несколько решений, но все квадраты получаются из других симметрией относительно средних линий или диагонали. (слайд 16)
Задача 6. Даны числа 2, 4, 6, 8, 10, 12, 14, 16, 18. Впишите их в клетки квадрата так, чтобы в любом направлении получилось в сумме одно и то же число.
Один из вариантов решения на слайде. (слайд 17)
Задача 7. Сравните условие задач 1 и 6 и подумайте, как можно было решить задачу, зная решение задачи 1.
(Числа из задачи 6 в два раза больше соответствующих чисел задачи 1. Поэтому можно каждое число квадрата из задачи 1 просто удвоить и получить искомый квадрат.)
Существуют различные способы построения магических квадратов. Рассмотрим метод террас, который придумали древние китайцы. Следуя этому методу надо «естественный» числовой квадрат повернуть относительно центра на половину прямого угла (слайд 19) и отделить квадратной рамкой таблицу 3´3. (слайд 20)Числами, записанными вне рамки, и образующими выступы («террасы»), заполняем пустые клетки у противоположной стороны таблицы. (слайд 21)
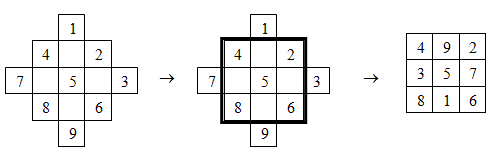
Аналогично можно построить любой квадрат нечетного порядка. Заполним клетки магического квадрата 5´5 числами от 1 до 25. (слайды 22, 23, 24)
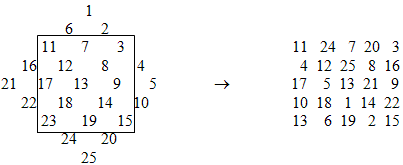
Для построения магического квадрата 4´4 наиболее простым и доступным является следующий метод: в «естественном» квадрате меняются местами дополнительные числа на главных диагоналях, а остальные остаются без изменения. (слайды 25, 26)
-
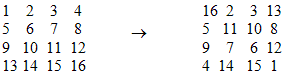
Исторически значимые магические квадраты
Квадрат Ло Шу
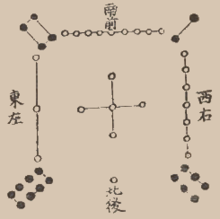
Изображение Ло Шу в книге эпохи Мин
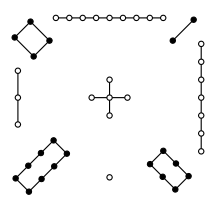
Единственный нормальный магический квадрат 3×3. Был известен ещё в Древнем Китае, первое изображение на черепаховом панцире датируется 2200г. до н.э..
9
2
3
5
7
8
1
6
Квадрат, найденный в Кхаджурахо (Индия)
Самый ранний уникальный магический квадрат обнаружен в надписи XI века в индийском городе Кхаджурахо:
12
1
14
2
13
8
11
16
3
10
5
9
6
15
4
Это первый магический квадрат, относящийся к разновидности так называемых «дьявольских» квадратов.
Магический квадрат Ян Хуэя (Китай)
В 13 в. математик Ян Хуэй занялся проблемой методов построения магических квадратов. Его исследования были потом продолжены другими китайскими математиками. Ян Хуэй рассматривал магические квадраты не только третьего, но и больших порядков. Некоторые из его квадратов были достаточно сложны, однако он всегда давал правила для их построения. Он сумел построить магический квадрат шестого порядка, причем последний оказался почти ассоциативным (в нем только две пары центрально противолежащих чисел не дают сумму 37)]:
29
2
4
13
36
9
11
20
22
31
18
32
25
7
3
21
23
14
16
34
30
12
5
28
6
15
17
26
19
1
24
33
35
8
10
Квадрат Альбрехта Дюрера
Фрагмент гравюры Дюрера «Меланхолия»
Магический квадрат 4×4, изображённый на гравюре Альбрехта Дюрера «Меланхолия I», считается самым ранним в европейском искусстве. Два средних числа в нижнем ряду указывают дату создания гравюры (1514).
3
2
13
5
10
11
8
9
6
7
12
4
15
14
1
Сумма чисел на любой горизонтали, вертикали и диагонали равна 34. Эта сумма также встречается во всех угловых квадратах 2×2, в центральном квадрате (10+11+6+7), в квадрате из угловых клеток (16+13+4+1), в квадратах, построенных «ходом коня» (2+8+9+15 и 3+5+12+14), в прямоугольниках, образованных парами средних клеток на противоположных сторонах (3+2+15+14 и 5+8+9+12). Большинство дополнительных симметрий связано с тем, что сумма любых двух центрально симметрично расположенных чисел равна 17.
Квадраты Генри Э. Дьюдени и Аллана У. Джонсона-мл.
Если в квадратную матрицу n × n заносится не строго натуральный ряд чисел, то данный магический квадрат - нетрадиционный. Ниже представлены два таких магических квадрата, заполненные простыми числами (хотя 1 в современной теории чисел не считается простым числом). Первый имеет порядок n=3 (квадрат Дьюдени); второй (размером 4x4) - квадрат Джонсона. Оба они были разработаны в начале двадцатого столетия:
1
43
13
37
61
31
73
7
3
61
19
37
43
31
5
41
7
11
73
29
67
17
23
13
Есть еще несколько подобных примеров:
89
71
113
59
5
47
29
101
1
823
821
809
811
797
19
29
313
31
23
37
89
83
211
79
641
631
619
709
617
53
43
739
97
227
103
107
193
557
719
727
607
139
757
281
223
653
499
197
109
113
563
479
173
761
587
157
367
379
521
383
241
467
257
263
269
167
601
599
349
359
353
647
389
331
317
311
409
307
293
449
503
523
233
337
547
397
421
17
401
271
431
433
229
491
373
487
461
251
443
463
137
439
457
283
509
199
73
541
347
191
181
569
577
571
163
593
661
101
643
239
691
701
127
131
179
613
277
151
659
673
677
683
71
67
61
47
59
743
733
41
827
3
7
5
13
11
787
769
773
419
149
751
Последний квадрат, построенный в 1913 г. Дж. Н.Манси, примечателен тем, что он составлен из 143 последовательных простых чисел за исключением двух моментов: привлечена единица, которая не является простым числом, и не использовано единственное чётное простое число 2.
Квадраты с дополнительными свойствами
Дьявольский магический квадрат
Дьявольский квадрат или пандиагональный квадрат - магический квадрат, в котором также с магической константой совпадают суммы чисел по ломаным диагоналям (диагонали, которые образуются при сворачивании квадрата в тор) в обоих направлениях.
Существует 48 дьявольских квадратов 4×4 с точностью до поворотов и отражений. Если принять во внимание ещё и симметрию относительно торических параллельных переносов, то остаётся только 3 существенно различных квадрата:
8
13
12
14
11
2
7
4
5
16
9
15
10
3
6
1
12
7
14
8
13
2
11
10
3
16
5
15
6
9
4
1
8
11
14
12
13
2
7
6
3
16
9
15
10
5
4
Пандиагональные квадраты четвёртого порядка обладают рядом дополнительных свойств, за которые их называют совершенными. Совершенных квадратов нечётного порядка не существует. Среди пандиагональных квадратов двойной чётности выше 4 имеются совершенные.[7]</</p>
Пандиагональных квадратов пятого порядка 3600. С учётом торических параллельных переносов имеется 144 различных пандиагональных квадратов. Один из них показан ниже.
15
24
8
17
9
18
2
11
25
12
21
10
19
3
20
4
13
22
6
23
7
16
5
14
Разломанные диагонали пандиагонального квадрата
Если пандиагональный квадрат еще и ассоциативный, то он носит название идеальный. Пример идеального магического квадрата:
32
70
26
28
69
22
36
65
40
81
2
39
77
7
44
73
6
62
10
51
58
18
47
57
14
52
66
23
34
71
19
33
67
27
29
4
45
74
3
41
79
8
37
78
53
55
15
49
63
11
48
59
16
30
68
25
35
64
24
31
72
20
76
9
38
75
5
43
80
1
42
17
46
60
13
54
56
12
50
61
-
Решение математических задач на логические цепочки.
Использование презентаций 1-17
-
Итоги урока
Какую тайну магических квадратов вы открыли сегодня на занятии? Что вам в этом помогло?
-
Домашнее задание.
Придумать магический квадрат.
15