Конспект урока по математике о теме Логарифм

Открытый урок в 11 классе

Логарифм.

Цель: повторение, обобщение и систематизация темы «Логарифмы».

Задачи:

1. применение свойств логарифмов в ходе преобразования выражений, содержащих логарифмы

2. Способствование формированию умений применять приемы: обобщения, сравнения, развитие мышления, внимания, памяти.

3. Воспитание у учащихся чувство ответственности, организованности, товарищества, настойчивости и упорства в достижении цели.

Тип урока: урок комплексного применения знаний

Вид урока: урок - деловая игра

Оборудование урока: ИД, оценочный лист, презентация

«Гений - это 1 ℅ вдохновения

и 99 ℅ потения» Эдисон

Ход урока

1. Организационный момент. Психологический настрой урока

Сегодня я предлагаю объективно оценить уровень своих знаний по теме «Логарифм.» в форме деловой игры. Хочу обратить ваше внимание на то, что решение подобных заданий включают в себя тесты на ЕНТ.

2. Актуализация знаний.

1. Разминка. Цифровой диктант.

Цифровой диктант (прием из программированного обучения, где основой является идея о постоянной обратной связи, эффективно используется для быстрой фронтальной проверки усвоения и закрепления знаний). Учитель произносит утверждение и, если ученик согласен, то он ставит единицу (1), если нет - нуль (0). В результате получится число. Все, кто получил правильное число, получит «плюс» за данный этап урока.

1. уравнение - это равенство, содержащее букву, значение которой надо найти. (1)

2. чтобы найти неизвестное слагаемое, надо к сумме прибавить известное слагаемое (0)

3. решить уравнение - значит найти все его корни или убедиться, что корней нет. (1)

4. 100/4=20. (0)

5. чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое. (1)

6. корнем уравнения называется значение буквы, при котором из уравнения получается верное числовое неравенство. (1)

7. 120 больше 60 на 2. (0)

1010110

2. Фронтальный опрос. Дайте определение логарифма. Записать основное логарифмическое тождество. (Если ученик пишет: 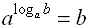, тогда следующий вопрос звучит так: Для каких a и b справедливо это тождество?

3. 1 ряд. Математическая эстафета «Кто больше?» записать логарифмические свойства

4. 2 ряд. Продолжить

6. 3 ряд. Найди ошибку

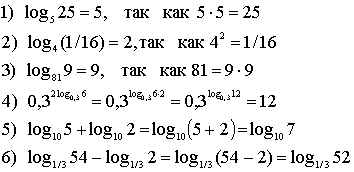
7. Устно

Вычислить: , , ,, , ,

, , , , ,

, ,

Решить уравнение: , , ,

, , , , , ,

3. Индивидуальное задание.

1. Решение системы уравнений

2. Решение уравнений

3. Найти значение выражения

4. Отдых. Логарифмическая комедия.

"Комедия" начинается с неравенства 1/4 >1/8 , бесспорно правильного. Затем следует преобразование , тоже не внушает сомнения. Большему числу соответствует больший логарифм, значит:

lg>lg, 2lg1/2 >3lg1/2 .

После сокращения на lg1/2 имеем 2>3.

В чем ошибка этого доказательства?

Решение: Ошибка была допущена при сокращении на lg1/2; так как lg1/2 < 0, то при сокращении на

lg 1/2 необходимо было изменить знак неравенства, т.е. 2<3.

5. Историческая справка

Из истории: - Джон Непер (1550-1617) - известный английский математик, шотландский барон. Непер вошел в историю математики как изобретатель логарифмов (1594 г), составитель первой таблицы логарифмов, которой он посвятил 20 лет своей жизни.

Его современник, Бриг, прославившийся позднее изобретением десятичных логарифмов, отправился в Шотландию, чтобы посетить изобретателя логарифмов. При встрече Бриг сказал: «Я предпринял это долгое путешествие с единственной целью видеть Вас и узнать с помощью какого орудия остроумия и искусства были Вы приведены к первой мысли о логарифмах. Впрочем, теперь я больше удивляюсь тому, что никто не нашел их раньше, - настолько кажутся они простыми после того, как о них узнаешь.»

Более 300 лет логарифмы использовались для облегчения вычислений. Их основное достоинство - способность сводить умножение к сложению. Были составлены обширные таблицы логарифмов чисел, с помощью которых можно легко переходить от чисел к их логарифмам и обратно.

Все таблицы логарифмов до 1950 г. являлись перепечаткой или сокращением таблиц Генри Бриггса (1561 -1630)

За 300 лет не нашлось никого, кто повторил бы эту работу.. Любопытно, что немного раньше Бриггса таблицу натуральных логарифмов составил Джон Непер (1550-1617)

Изобретатель первых логарифмических таблиц, Непер, так говорит о своих побуждениях : « Я старался, насколько мог и умел, отделяться от трудности и скуки вычислений, докучность которых отпугивает весьма многих от изучения математики»

В самом деле, логарифмы чрезвычайно облегчают и ускоряют вычисления, не говоря уже о том, что они дают возможность производить такие операции, выполнение которых без их помощи очень затруднительно (извлечение корня любой степени).

Не без основания писал Лаплас, что «изобретение логарифмов, сокращая вычисления нескольких месяцев в труд нескольких дней, словно удваивает жизнь астрономов».

6. Решение задания встречающихся в тестах на ЕНТ, 2016г

7. Тест. Критерии оценки: «5» - 9-10 баллов; «4» - 7- 8 баллов; «3» - 5- 6 баллов.

Проверочный тест.

1. Вычислите . 1) 28 2) 13 3) 75 4) 30

2. Вычислите 1) 0 2) 1 3) 4 4) 8

3. Вычислите . 1) 7 2) - 2 3) - 1 4) 1

4. Вычислите . 1) 45 2) 49 3) 47 4) 49 -

5. Найдите значение выражения . 1) 3,5 2) ln 32 3) ln 124 4) 32

6. Укажите значение выражения . 1) 2) 10 3) 100 4)

7. Решите уравнение 1) ± 7 2) 3) 4) Ø

8. Решите неравенство . 1) (1; 1,25) 2) (1; + ∞) 3) (1,25; + ∞) 4) (- ∞; 1,25)

9. Найдите область определения функции .

1) (0; 9); (9; + ∞) 2) 9 3) (0; + ∞) 4) (1; + ∞)

10. Укажите область значений функции

1) (0; + ∞) 2) (- ∞ 7) 3) (7; + ∞) 4) (- ∞ + ∞)

Ответы к тесту: (слайд 18)

1 2 3 4 5 6 7 8 9 10

3 1 2 3 1 2 4 3 1 4

8. Домашнее задание. Из тестовых заданий выберите задания по данной теме и решите.

Необязательное задание. Доказать

Доказательство на дом

, так как

9. Рефлексия

1) Какие цели на уроке мы ставили?

2) Достигли ли мы их?

3) Каким способом мы их достигли?

10. Подведение итогов деловой игры. Выставление оценок каждому ученику по результатам в листе учета знаний.

3