Конспект урока по теме: «Соотношения между тригонометрическими функциями одного и того же угла»

9 класс. Конспект урока по теме: «Соотношения между тригонометрическими функциями одного и того же угла»

(Учебник Атанасян Л.С., Бутузов В.Ф. и др. «Геометрия, 7-9»)

Тип урока: урок изучения нового материала и первичного закрепления.

Цели:Вывести основное тригонометрическое тождество; сформировать умения применять его для упрощения выражений, нахождения тригонометрических функций.

Развивающая

развивать мышление, память, развивать умение анализировать, строить аналогии, развивать математически грамотную речь: развитие самостоятельности; познавательного интереса (через исторические экскурсы).

Воспитательная:

воспитание сознательного отношения к учебе; доброжелательное отношение друг к другу (работа в парах, группах); ответственность за полученный результат, воспитание учебной самостоятельности.

Дидактическая цель:

создать условия для осознания и осмысления блока новой учебной информации.

Знания и умения:

• знать основное тригонометрическое тождество,

• уметь его применять для упрощения выражений и нахождения тригонометрической функции.

Оборудование к уроку:

• указка;

• треугольник;

• циркуль;

• цветные мелки.

• Приготовить тригонометрический круг на доске.

• Раздать карточки для рефлексии и чистые листы бумаги.

Сегодня на уроке будем изучать и совершать экскурсы в историю математики по приготовленным вами рефератам.

1. Организационный момент

Французский писатель Анатоль Франс (1844-1924) однажды заметил: «Учиться можно только весело… Чтобы переваривать знания, надо поглощать их с аппетитом». Я предлагаю следовать этому совету писателя, будем активны, внимательны, будем поглощать знания с большим желанием, ведь они пригодятся вам в вашей дальнейшей жизни.

Повторение.

1. Какую тему изучаем?

1. Что такое тригонометрия? (доклад Таныгиной Оли)

2. Сегодня мы узнаем, как обозначали синус, косинус, тангенс, котангенс в разные времена (доклад Кауменовой Ж.)

2. Целеполагание и мотивация.

Сегодня мы будем продолжать изучать тригонометрические выражения, а именно познакомимся с соотношениями между тригонометрическими функциями одного и того же угла, т.е. узнаем как связаны sin α, cos α одного и того же угла. Для этого повторим определения sin α, cos α.

sin α = y = R * sin α

cos α = x = R * cos α

3. Актуализация

Так как точка В принадлежит окружности с центром в начале координат, радиус которой равен R, то ее координаты удовлетворяют уравнению окружности

+ = R²

подставляем вместо х и у в это уравнение полученные выше выражения, получаем

(R α)² + (R sin α)² =R²

R²² α + R² sin² α = R² /: R²

² α + sin² α = 1

или

- основное тригонометрическое тождество

Оно говорит о том, как связаны между собой синус и косинус одного и того же угла.

Итак, как же они связаны?

Для чего нужно знать это тождество?

1. Чтобы упрощать выражения, например,

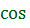1. ² α = 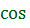² α + sin² α - 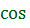² α = sin² α

Первичное закрепление № 755 (б,г) , № 757 (г) - учащиеся выполняют у доски.

2. Ещё для чего изучаем это тождество? Вы сможете ответить на этот вопрос после работы в парах:

- выразите из основного тригонометрического тождества sin α,

- выразите из основного тригонометрического тождества α и подумайте над тем, как верно получить окончательный ответ. От чего зависит окончательный ответ?

Ответы групп: sin α = 1- ² α

От чего зависит sin α (от того, какой четверти принадлежит угол)

α = 1- sin² α - аналогично.

Итак, для чего еще используют основное тригонометрическое тождество?

3. Для нахождения значений тригонометрических функций.

Дано sin α = ; α π

Найти α

sin² α = 1 - ² α.

Так как α угол II четверти , то его косинус отрицательный, значит

α = - 1- sin²α = - 1- (² = - 1- ( = - = - =-

Посмотрите внимательно записи на доске. Такой вид появился не сразу, о современном виде тригонометрии написала реферат И. Перминова.

Продолжаем выполнять упражнения: № 760 (а).

Решение №766 (а) - работа в группах.

Самостоятельно №755 (д);

№1, №3, №5- № 762(а): + = 1 - верно, для угла β может выполняться данное условие

№ 2, № 4, № 6 - № 762 (б)

Ответы для групп:

+ = 1 - неверно. Для угла β не может выполняться данное условие

Ответы для групп:1, №3, №5 №755 (д)

(1-sin α) (1+ sin α) = /……..

№762 (а)

Sin² β +cos² β = 1

)² + (² = 1

+ = 1 - верно

Поэтому для угла β может выполняться данное условие

№ 2, № 4, № 6 - № 755 (е)

(cos α - 1) (1+cos α) =…….

№762 (б)

Sin² β +cos² β = 1

) ² + ( ) ² = 1 - неверно

+ = 1- неверно

Таким образом, для угла β не может выполняться данное условие

Подводим итоги работы в группах, выставляем оценки.

4. Рефлексия по розданным печатным листочкам.

Чем будем заним атьсяна следующем уроке? (Учиться находить значения tg α, ctg α).

Понравились ли вам доклады? (Оценки ребятам за выступления).

5. Домашнее задание. Параграф 31читать. №756, №761 (а,б), №763 решить различными способами. Для сильных учащихся № 922 (а)