Разработка урока по математике в 6 классе по теме«Решение прикладных задач с применением пропорции.»

Тема урока «Решение прикладных задач с применением пропорции.»
Цели урока:
дидактическая:
-обобщить и систематизировать знания об отношении двух чисел и пропорции;
-показать использование пропорции при решении задач экономического и прикладного содержания;
-формировать навыки решения задач с помощью пропорции;
воспитательная
-воспитывать личностное отношение к изучаемым знаниям и умение извлекать нравственные ценности из их содержания;

-создать условия для формирования личностных позитивных качеств учеников и атмосферы сотрудничества, чередуя коллективные и индивидуальные формы работы;

-воспитывать в учениках средствами урока уверенность в своих силах;
развивающая
-развивать навыки устной и письменной, речи, вычислительные навыки;

-развивать логическое мышление, способность четко формулировать свои мысли;

-развивать навыки групповой самоорганизации;
-развивать мышление, необходимое образованному человеку для полноценного функционирования в современном обществе.

Ход урока

Деятельность учителя

Деятельность ученика

1. Орг. момент

Приветствие, проверка готовности учащихся к уроку. Раскрытие общей цели урока.

- Французский писатель Анатоль Франс однажды заметил: «Учиться можно только весело... Чтобы переваривать знания, надо поглощать их с аппетитом». Так вот, давайте сегодня на уроке будем следовать этому совету писателя, будем активны, внимательны, будем поглощать знания с большим желанием. И данное высказывание будет эпиграфом- девизом нашего учебного занятия.
Сегодня у нас урок по теме «Решение прикладных задач с применением пропорции.».

Сформулируем цель нашего урока:

2. Повторение.

Ответить на вопросы:

1. Что такое пропорция.

2. Назовите крайние и средние члены пропорции

3. Сформулируйте основное свойство пропорции

4. Какие пропорциональные зависимости вам известны?

5. Когда пропорциональность является прямой?

6. Когда пропорциональность является обратной?

7. Где используются пропорции?

3.Мотивация учебной деятельности
Изучая ту или иную тему по математике, каждый из вас задумывается над вопросами: «Для чего мне нужны эти знания?», «Где я их смогу применить?». На сегодняшнем уроке мы попробуем ответить на эти вопросы

Математические знания и навыки необходимы практически во всех профессиях, прежде всего в тех, которые связаны техникой, экономикой. Несомненна необходимость применения математических знаний и математического мышления и врачу, и историку, и трудно оборвать этот список, настолько важно математическое образование для профессиональной деятельности в наше время.

Давайте подумаем, какие профессии требуют математических знаний, в частности, знаний по теме ПРОПОРЦИИ?

4.Работа в группах (каждой группе предлагается ряд задач. Группа должна выбрать, решить задачу , которая соответствует профессиональной деятельности; а затем отчитаться о работе группы)

• Частный предприниматель

• Повар

• Строитель

• Медик

Пропорция на службе у частного предпринимателя
Основная идея проекта: частному предпринимателю в своей деятельности приходится быть не только специалистом, соответствующего профиля, но и менеджером, и маркетологом, и бухгалтером. Поэтому частному предпринимателю необходим определённый багаж экономических знаний и умение решать задачи с помощью пропорции.
В ноябре фонд заработной платы на фирме составил 85000 рублей. При этом на фирме работало 4 человека. Сколько составит фонд заработной платы фирмы в декабре, если количество рабочих увеличится до 6 человек?
Пропорции в медицине

Основная идея проекта: медицинскому работнику необходимо умение решать задачи с помощью пропорции для того, чтобы правильно рассчитать дозировку и концентрацию лекарственных препаратов. Также проводя профилактическую работу о вреде курения, можно рассмотреть такую задачу:

В России ежегодно умирают 500 000 мужчин в среднем возрасте. 42 % из них умирают из-за болезней, связанных с курением. Сколько человек могли бы продолжать жить, если бросили курить?

Пропорции на кухне

Повар - это не просто человек, которые колдует на кухне, и из- под рук которого выходят вкуснейшие и красивейшие блюда. Повару необходимы знания о составе пищи и ее калорийности, хранении продуктов, Да и кушанье необходимо подать красиво, создавая из каждого блюда уникальный, неповторимый натюрморт.
Задача N1
Повару необходимо приготовить 13 порций бифштекса по 200г в каждой. Cколько ему необходимо взять сырого мяса , если известно, что мясо при варке теряет 35% своей массы.
_________________________________

Пропорции в профессии «мастер общестроительных работ»

Для строительства стадиона 5 бульдозеров расчистили площадку за 210 мин. За какое время 7 бульдозеров расчистили бы эту площадку? - к доске вызывается один из учащихся, который рассуждает вслух, а остальные работают в тетрадях.

__________________________

Футболка стоила 1200 рублей. После снижения цены она стала стоить 972 рублей. На сколько процентов была снижена цена на футболку?

В городе N живет 250000 жителей. Среди них 15 % детей и подростков. Среди взрослых жителей 35% не работает (пенсионеры, студенты, домохозяйки и т.п.). Сколько взрослых жителей работает?

____________________________

Налог на доходы составляет 13% от заработной платы. Заработная плата Ивана Кузьмича равна 10000 рублей. Сколько рублей он получит после вычета налога на доходы?

4) Пословицы (резерв).

Пословицы, отражающие прямую зависимость:

• Чем дальше в лес, тем больше дров.

• Как аукнется, так и откликнется.

• Много снега, много хлеба.

• Как потопаешь, так и полопаешь.

• Выучишь правило, выполнишь верно задание.

• Кто много читает, тот много знает.

Пословицы, отражающие обратную зависимость:

• Тише едешь, дальше будешь.

• Меньше народа, больше кислорода.

• Лето собирает, зима съедает.

• Было густо, стало пусто.

• С большого грома - малый дождь.

• Меньше слов - больше дела.

Подведение итогов урока

- Итак, наш урок близится к концу. Давайте вспомним, какие цели мы ставили в начале урока. Удалось ли их достичь? Что запомнилось на уроке?

Решая задачи на сегодняшнем уроке, мы выяснили, что пропорция применяется:

8. Информация о домашнем задании. Инструктаж по его выполнению

-Решить оставшиеся задачи.
- Подобрать, а лучше придумать самим, задачи с использованием прямой и обратной пропорциональных зависимостей. Оформить решение задач в тетради

- Спасибо за работу!

Запись темы урока в тетрадь

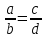
При решении задач

Называют профессии:

• Частный предприниматель

• Повар

• Строитель

• Медик

1 ученик работает у доски, остальные в тетради

______________________________________

Решение
13*200=2600Г. Из условия следует, что при варке сохранится 65% массы. По правилу пропорции; X кг соответствует 100%, 2600г соответствует 65%. Тогда x = 2600*100/65=4000г. Ответ:4кг

Решение:

Краткая запись.

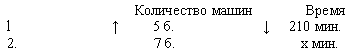
Зависимость между количеством машин и временем работы обратно пропорциональна, поэтому стрелочки направляем в противоположные стороны, составляем пропорцию: 7 : 5 = 210 : х, находим неизвестный крайний член, для этого произведение средних членов делим на известный крайний член. Пишем: х = = 150 (мин).

Ответ: 150 минут.

_____________________________________

Определим, сколько процентов от 1200 рублей составляет сниженная цена. 1200 рублей (величина, с которой сравниваем) принимаем за 100%, 972 рубля это х %. Составляем пропорцию:

1200 рублей - 100%

972 рубля - х %

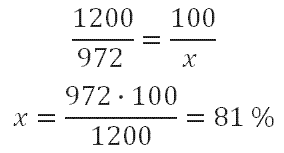
То есть 972 это 81% от 1200 рублей.

Значит, цена снизилась на 100-81=19%.

Ответ: 19

______________________________________

Почему-то именно эту задачу редко решают правильно? Дело в том, что «15 процентов» или «35 процентов» - величины относительные. Каждый раз за сто процентов могут приниматься разные величины. Помните правило: за сто процентов принимается в каждом случае то, с чем мы сравниваем. Итак, дети и подростки составляют 15% от 250000 жителей. Значит, их число - это 15% от 250000,

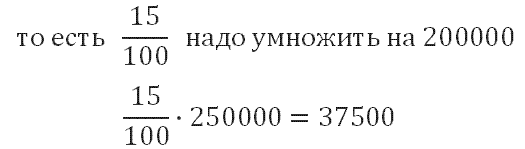
Получили, что в городе 37500 детей и подростков. Следовательно, взрослых в городе 250000-37500=212500 человек.

Среди взрослых 35% не работает. Теперь за 100% мы принимаем число взрослых. Получается, что число не работающих взрослых жителей равно 35% от 212500, составляем пропорцию:

212500 - 100%

х - 35%

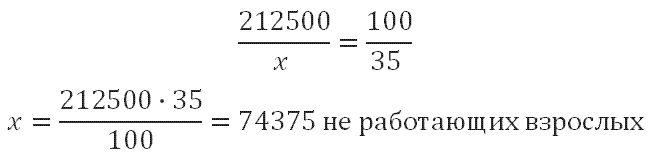Значит, число работающих взрослых составляет 212500-74375=138125 человек. При решении данного типа задач будьте внимательны, есть соблазн записать промежуточный результат, например, 74375. Внимательно читайте условие, и не теряйте из виду, что необходимо найти.

Ответ: 138125

________________________________

Составляем пропорцию и находим 13% от 10000 рублей:

10000 рублей - 100%

х рублей - 13 %

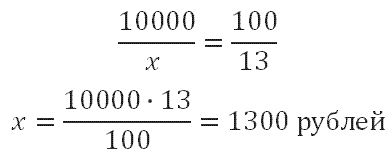
Иван Кузьмич получит после вычета: 10000 -1300=8700 рублей.

Ответ: 8700