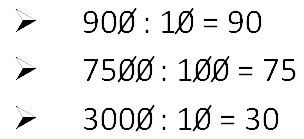Таблица по теме Признаки делимости

</<font face="Times New Roman, serif">Признаки

Запомни

Пример

Признак делимости на 2

Число делится на 2, если его последняя цифра делится на 2 или является нулём.

• 52 делится на 2. Последняя цифра 2 делится на 2 нацело (2 : 2 = 1).

• 300 делится на 2. Последняя цифра 0.

• 11 не делится на 2. Последняя цифра 1 не делится на 2.

Признак делимости на 4

Число делится на 4, если две его последние цифры нули или образуют число, делящееся на 4.

• 548 делится на 4. Две последние цифры 48 делятся на 4 нацело (48 : 4 = 12).

• 600 делится на 4. Две последние цифры нули.

• 755 не делится на 4. Две последние цифры 55 не делятся на 4.

Признак делимости на 8

Число делится на 8, если три последние его цифры нули или образуют число, делящееся на 8.

• 1128 делится на 8. Три последние цифры 128 делятся на 8 нацело (128 : 8 = 16).

• 7000 делится на 8. Три последние цифры нули.

• 6755 не делится на 4. Три последние цифры 755 не делятся на 8.

Признак делимости на 3

Число делится на 3, если сумма всех его цифр делится на 3.

• 153 делится на 3. Сумма всех его цифр: 1 + 5 + 3 = 9 делится на 3 (9 : 3 = 3).

• 300 делится на 3. Сумма всех его цифр: 3 + 0 + 0 = 3 делится на 3 (3 : 3 = 1).

• 11 не делится на 3. Сумма всех его цифр: 1 + 1 = 2 не делится на 3.

Признак делимости на 6

Число делится на 6, если оно делится одновременно на 2 и на 3.

• 126 делится на 6. По признаку делимости на 2 оно делится на 2 (последняя цифра 6 делится на 2). По признаку делимости на 3 оно также делится на 3 (сумма цифр числа 1 + 2 + 6 = 9 делится на три). Это означает, что 126 делится на 6.

• 801 не делится на 6. По признаку делимости на 2 оно не делится на 2.

• 757 не делится на 6. По признаку делимости на 3 оно не делится на 3.

Признак делимости на 9

Число делится на 9, если сумма всех его цифр делится на 9.

• 486 делится на 9. Сумма всех его цифр: 4 + 8 + 6 = 18 делится на 9 (18 : 9 = 2).

• 9198 делится на 9. Сумма всех его цифр: 9 + 1 + 9 + 8 = 27 делится на 9 (27 : 9 = 3).

• 55 не делится на 9. Сумма всех его цифр: 5 + 5 = 10 не делится на 9.

Признак делимости на 5

Число делится на 5, если его последняя цифра 5 или 0.

• 155 делится на 5. Последняя цифра 5.

• 800 делится на 5. Последняя цифра 0.

• 61 не делится на 5. Последняя цифра 1.

Признак делимости на 25

Число делится на 25, если его две последние цифры нули или образуют число, которое делится на 25.

• 675 делится на 25. Две последние цифры образуют число 75, которое делится на 25. (75 : 25 = 3) Это означает, что 675 делится на 25.

• 3900 делится на 25. Две последние цифры нули.

• 345 не делится на 25. Две последние цифры образуют число 45, которое не делится на 25.

Признак делимости на 10,100 и 1000.

10 делятся нацело только те числа, последняя цифра которых нуль.

На 100 делятся нацело только те числа, две последние цифры которых нули.

На 1000 делятся нацело только те числа, три последние цифры нули.

Чтобы было проще делить на 10, 100 и 1000, просто зачеркивайте одинаковое количество нулей в обоих числах.

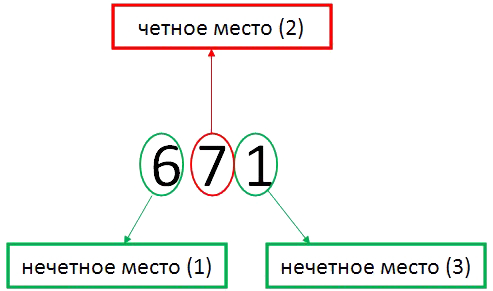
Признак делимости на 11

Число делится на 11, если сумма цифр, которые стоят на четных местах равна сумме цифр, стоящих на нечетных местах, либо отличается от неё на 11.

• Проверим, делится ли 671 на 11 .

Итак, цифры которые стоят на нечетных местах - это 6 (стоит на первом месте) и 1 (стоит на третьим месте). Цифра, которая стоит на четном месте это 7 (стоит на втором месте). 6 + 1 = 7. Сумма цифр стоящих на нечетном месте равна сумме цифр на четном месте, значит 671 делится на 11.

• Проверим делится ли 3905 на 11 .

Цифры которые стоят на нечетных местах - это 3 (стоит на первом месте) и 0 (стоит на третьим месте). Цифры, которые стоят на четном месте это 9 (стоит на втором месте) и 5 (стоит на четвертом месте) 3 + 0 ≠ 9 + 5 → 3 ≠ 14 Сумма цифр, стоящих на нечетном месте, не равна сумме цифр на четном месте, но суммы цифр отличаются ровно на 11. 14 − 3 = 11. Значит 3905 делится на 11.