- Учителю
- Методическая разработка для зачётов по геометрии 8 класс
Методическая разработка для зачётов по геометрии 8 класс
Зачетная система по геометрии.
8 класс. Атанасян Л.С. И ДР.
Первый зачет
Четырёхугольники.
Тема: «Четырехугольники». Всего 14 час.
Планирование: 14 /час/.
-
Многоугольники. 2
-
Параллелограмм и трапеция. 2
-
Прямоугольник. Квадрат. Ромб . 3
-
Симметричные фигуры. 2
-
Закрепление. 1
-
Зачёт 1 1
-
Задачи на построение. 2
8. КОНТРОЛЬНАЯ РАБОТА 1
Основные понятия и определения:
-
понятия многоугольника,
-
понятие выпуклого многоугольника (сумма углов ),
-
определение (свойства, признаки ) параллелограмма,
-
определение (свойства, признак р/б трапеции ) трапеции,
-
определение (свойства, признаки) прямоугольника,
-
определение(свойства , признаки ) ромба,
-
определение (свойства , признаки) квадрата,
-
осевая и центральная симметрия.
Зачёт можно провести на одном уроке ,если теоретические вопросы спросить сначала сильных, подготовленных учеников ,которые ,ответив , становятся консультантами , и остальные учащиеся теорию отвечают им.( 15 - 20 мин.) Далее раздаются карточки с разноуровневыми задачами.
Задача №1 -обязательный уровень (оц. 3).Задачи № 2,3 - повышенный уровень ( оц. 4;5)
На каждом втором уроке новой темы главы провожу самостоятельную работу из 4 - х вариантов.(см.приложение 1)Первая часть - обязательный уровень. Вторая часть - повышенный уровень. Оценки соответствуют(критериями оценки здесь может послужить балловая система ).
Приложение 1: 




Второй зачёт.
Площадь .Теорема Пифагора.(14 ч.)
Планирование :
-
Площадь многоугольника. -2
-
Площадь параллелограмма ,треугольника ,трапеции.- 6
-
Теорема Пифагора - 3
-
Решение задач - 1
-
Зачёт - 1
-
Контрольная работа по теме « Площадь» -1
На каждом втором уроке - самостоятельная работа ( 4 варианта ) Приложение 2.
Билеты к зачёту по геометрии 8 класс
Билет №1. «5»
1.Расскажите, как измеряются площади многоугольников.
2. Площадь прямоугольника равна ![]() Найдите
стороны этого прямоугольника, если одна из них в три раза больше
другой.
Найдите
стороны этого прямоугольника, если одна из них в три раза больше
другой.
3. основание одного треугольника 10 см, его высота 4 см. основание другого треугольника 20 см. какова должна быть его высота, проведённая к этой стороне, чтобы треугольники были равны?
Билет №2. . «5»
1.Сформулируйте основные свойства площадей мно-
гоугольников
2. Найдите площадь прямоугольника, если одна из его
сторон равна 5 см, а угол между диагоналями равен ![]()
3. Катеты прямоугольного треугольника равны 6 и 8
см., гипотенуза 10 см. Вычислите высоту, проведён-
ную к гипотенузе.
Билет №3. . «5»
1.Сформулируйте и докажите теорему о вычислении площади прямоугольника.
2. Площадь параллелограмма равна ![]() Найдите
высоту параллелограмма, проведённую к стороне равной 12 см.
Найдите
высоту параллелограмма, проведённую к стороне равной 12 см.
3. Найдите площадь трапеции с основаниями AD и BC, если АD=12см, ВС=6см, СD=5см, АС=13см.
Билет №4. . «5».
1. Сформулируйте и докажите теорему о вычислении площади параллелограмма.
2. Диагональ параллелограмма равна его стороне.
Найдите площадь параллелограмма, если одна из его
сторон равна 14см, а один из углов равен ![]()
3. Найдите площадь треугольника, стороны которого
равны 6см, 8см и 10см.
Билет №5. . «5»
1. Сформулируйте и докажите теорему о вычисле-
нии площади треугольника. Как вычислить пло-
щадь прямоугольного треугольника по его кате-
там?
2. Найдите сторону ромба, если его диагонали
равны 12см и 16см.
3. Найдите площадь равностороннего треугольни-
ка, сторона которого равна 12см.
Билет №6. . «5»
1. Сформулируйте и докажите теорему об отношении площадей треугольников, имеющих по равному углу.
2. Стороны АВ и ВС треугольника АВС равны соот-
ветственно 8см и 4,8см, а высота, проведённая к сто-
роне АВ, равна 6см. найдите высоту, проведённую
к стороне ВС.
3. Вычислите площадь трапеции АВСD с основани-
ями AD и ВС, если AD=20см, ВС=4см, АВ=16см и
угол а равен ![]()
Билет №7. «4»
1. Сформулируйте и докажите теорему о вычисле-
нии площади трапеции.
2. Найдите площадь равнобедренной трапеции,
если его основания равны 8см и 12см, а боковая
сторона - 10см.
3. Вычислите сторону квадрата, если его площадь
равна ![]()
Билет №8. «4»
1. Сформулируйте и докажите теорему Пифагора.
2. Найдите площадь равнобедренного треугольника,
если его основание равно 10см, а боковая сторона
равна 13см.
3. Стороны параллелограмма равны 6см и 4см. Одна
из высот равна 5 см. Найдите другую высоту. Сколь-
ко решений имеет задача?
Билет №9. «4»
1. Сформулируйте и докажите теорему, обратную
теореме Пифагора.
2. Вычислите площадь ромба, если его сторона равна
10см, а один из углов равен ![]()
3. Вычислите неизвестную сторону прямоугольника,
если его площадь и одна из сторон соответственно равны ![]() и 15см.
и 15см.
Билет №10. «4»
1. Какие треугольники называются пифагоровыми?
Приведите примеры пифагоровых треугольников.
2. Выясните вид треугольника, если его стороны
равны 6см, 8см и 10см.
3. Площадь земельного участка равна 250 ![]() . Чему
. Чему
равна площадь этого участка в квадратных метрах?
Билет №11. «4»
1. Сформулируйте теорему о площади прямоуголь-
ника.
2. Найдите площадь равностороннего треугольни-
ка, сторона которого равна 12см.
3. Площадь параллелограмма равна ![]() Найдите
высоту параллелограмма, проведённую к стороне равной 12 см.
Найдите
высоту параллелограмма, проведённую к стороне равной 12 см.
Билет №12. «4»
1. Сформулируйте теорему о площади параллело-
грамма.
2. . Катеты прямоугольного треугольника равны 6 и 8
см., гипотенуза 10 см. Вычислите высоту, проведён-
ную к гипотенузе.
3. Вычислите площадь ромба, если его сторона равна
10см, а один из углов равен ![]()
Билет №13. «4»
1.Сформулируйте теорему о площади треугольни-
ка.
2. Найдите площадь прямоугольника, если одна
из его сторон равна 5 см, а угол между диагоналя-
ми равен ![]()
3. Найдите площадь треугольника, стороны кото-
рого
равны 6см, 8см и 10см.
Билет №14. «4»
1. Сформулируйте теорему о площади трапеции.
2. Стороны АВ и ВС треугольника АВС равны соот-
ветственно 8см и 4,8см, а высота, проведённая к сто-
роне АВ, равна 6см. найдите высоту, проведённую
к стороне ВС.
3. Вычислите площадь трапеции АВСD с основани-
ями AD и ВС, если AD=20см, ВС=4см, АВ=16см и
угол а равен ![]()
Билет №15. «3»
1. Сформулируйте теорему Пифагора.
2. Вычислить площадь прямоугольника, если его
стороны равны 30см и 2,9см.
Билет №16. . «3»
1.Сформулируйте теореме, обратную теореме Пифаго-
ра.
2. Вычислить площадь прямоугольника, если его
стороны равны 34см и 0,6дм.
Билет №17. . «3»
1.Сформулируйте теорему Пифагора.
2. Вычислить площадь прямоугольника, если его
стороны равны 4м и 1,5см.
Билет №18. . «3»
1. Сформулируйте теорему о площади параллело-
грамма.
2. Вычислить площадь прямоугольника, если его
стороны равны 15см и 4, 5см.
Билет №19. . «4»
1.Сформулируйте теорему о площади треугольни-
ка.
2. Стороны АВ и ВС треугольника АВС равны
соответственно 8см и 4,8см, а высота, проведён-
ная к стороне АВ, равна 6см. найдите высоту,
проведённую к стороне ВС.
3. Вычислите площадь трапеции АВСD с основа-
ниями AD и ВС, если AD=20см, ВС=4см,
АВ=16см и угол а равен ![]()
Билет №20. . «4»
1.Сформулируйте теорему о площади трапеции.
2. Площадь прямоугольника равна ![]() Найдите
стороны этого прямоугольника, если одна из них в три раза больше
другой.
Найдите
стороны этого прямоугольника, если одна из них в три раза больше
другой.
3. основание одного треугольника 10 см, его высота
4 см. основание другого треугольника 20 см. Какова
должна быть его высота, проведённая к этой стороне,
чтобы треугольники были равны?
Билет №21. «3»
1.Сформулируйте теорему о площади треуголь-
ника.
2. Вычислить площадь прямоугольника, если его
стороны равны 3,5м и 1,5см.
Билет №22. «3»
1. Сформулируйте теорему о площади трапеции.
2. Вычислить площадь прямоугольника, если его
стороны равны 12дм и 3,4м.
Приложение 2:




Третий зачёт.
Тема: «Подобные треугольников»(19 ч.)
Планирование:
-
Определение подобных треугольников - 1
-
Признаки подобия треугольников -5
-
Контрольная работа - 1
-
Применение подобия к решению задач - 7
-
Соотношение между сторонами и углами треугольника - 3
-
Зачёт - 1
-
Контрольная работа по теме « Подобные треугольники».
Привожу пример карточек для самостоятельных работ ( приложение 3 ).
Эти же карточки я использую и на зачёте.(только меняю варианты)
Приложение 3:








Вопросы к зачёту.
Установите, истинны или ложны следующие высказывания.
ВАРИАНТ 1.
1. Два одноименных многоугольника называются подобными, если углы одного соответственно равны углам другого и сходственные стороны пропорциональны.
2. Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.
3. Два равносторонних треугольника всегда подобны.
4. Если три стороны одного треугольника соответственно пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
5. Периметры подобных многоугольников относятся как сходственные стороны.
6. Стороны одного треугольника имеют длины 3 см, 4 см и 6 см. Стороны другого треугольника равны 9 см, 14 см и 18 см. Подобны ли эти треугольники?
7. Два равнобедренных треугольника подобны, если их углы при вершине равны, и боковые стороны пропорциональны.
8. Два прямоугольных треугольника подобны, если имеют по равному острому углу.
9. Если два угла одного треугольника равны 60° и 50°, а два угла другого треугольника равны 50° и 80°, то такие треугольники подобны.
10. Если каждую сторону треугольника уменьшить в 2,5 раза, то получится треугольник, подобный первоначальному.
11. Два ромба всегда подобны.
12. Два равнобедренных треугольника подобны, если их основания пропорциональны.
13*. Катеты прямоугольного треугольника АВС равны 5 см и 12 см, меньший катет подобного ему прямоугольного треугольника МРК равен 15 см. Тогда гипотенуза треугольника МРК равна 39 см.
ВАРИАНТ 2.
1. Два треугольника называются подобными, если их углы соответственно равны и стороны пропорциональны.
2. Если два треугольника имеют по равному углу, а стороны, заключающие эти углы, пропорциональны, то такие треугольники подобны.
3. Два квадрата всегда подобны.
4. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники подобны.
5. Стороны одного треугольника имеют длины 4 м, 5 м и 6 м. Стороны другого треугольника равны 12 м, 8 м и 10 м. Тогда эти треугольники подобны.
6. Площади подобных треугольников относятся как квадраты сходственных сторон.
7. Два параллелограмма всегда подобны.
8. Если два угла одного треугольника равны 45° и 75°, а два угла другого треугольника равны 60° и 45°, то такие треугольники подобны.
9. Два прямоугольных треугольника подобны, если катеты одного треугольника соответственно. пропорциональны катетам другого.
10. Если каждую сторону треугольника уменьшить в 3 раза, то получится треугольник, подобный первоначальному.
11. Два равнобедренных треугольника подобны, если угол при основании одного треугольника равен углу при основании другого.
12. Два равнобедренных треугольника подобны, если их боковые стороны пропорциональны.
13*. Катет и гипотенуза треугольника МРК равны 6 м и 10 м, больший катет подобного ему треугольника АВС равен 16 м. Тогда меньший катет треугольника АВС равен 12 м.
Четвёртый зачёт.
Окружность.(17 ч.)
Планирование:
-
Касательная к окружности -3
-
Центральные и вписанные углы - 4
-
Четыре замечательные точки треугольника -3
-
Вписанная и описанная окружности -4
-
Решение задач -1
-
Зачёт -1
-
Контрольная работа -1.
Карточки с разноуровневыми задачами по данным темам (приложение 4)
Приложение 4.


![]()



![]()



![]()



![]()

Зачет №4 по теме «Окружность»
Проверка теоретических знаний.
Класс (фронтальная беседа).
-
Взаимное расположение прямой и окружности.
-
Определение касательной к окружности и ее свойство.
-
Какой угол называется центральным?
-
Какой угол называется вписанным? Чему равна его градусная мера?
-
Четыре замечательные точки треугольника.
-
Какая окружность называется вписанной? Описанной?
-
Какой многоугольник называется описанным? Вписанным?
-
Каким свойством обладают стороны четырехугольника, описанного около окружности?
-
Каким свойством обладают углы четырехугольника, вписанного в окружность?
-
Сформулируйте теорему об отрезках пересекающихся хорд.
Т-1.Заполните пропуски (многоточия), чтобы получилось верное высказывание.
ВАРИАНТ 1.
1. Точка, равноудаленная от всех точек окружности, называется ее ... .
2. Отрезок, соединяющий две точки окружности, называется ее ....
3. Все радиусы окружности ....
4. На рисунке 0(r) -окружность, АВ - касательная к ней; точка В называется ....
. 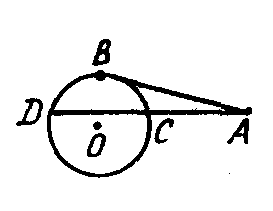
5. Прямая, имеющая с окружностью только одну общую точку, называется ... к окружности.
6. Угол между касательной к окружности и радиусом, проведенным в точку касания, равен ....
7. На рисунке АВ - диаметр окружности, С -точка, лежащая на окружности. Треугольник АСВ ... (вид треугольника).
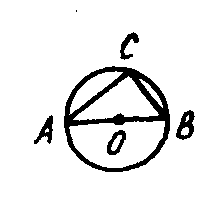
8. На рисунке АВ = 2ВС, АВ - диаметр окружности. Угол CAB равен ....
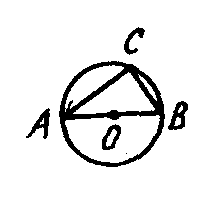
9.На рисунке хорды АВ и CD пересекаются в точке М. Угол ACD равен углу ....
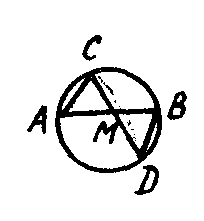
10.На рисунке О - центр окружности. Дуга АmВ равна 120°. Угол АВС равен .
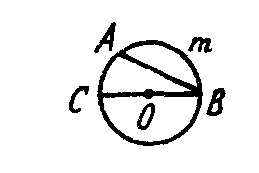
11.На рисунке АК = 24 см, KB = 9 см, CK = 12 см. Тогда KD = ...
. 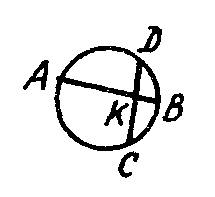
12*. На рисунке АВ = ВС = 13 см, высота BD = 12 см. Тогда ВК = ... , КС = ... .
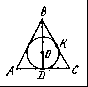
ВАРИАНТ 2.
1. Геометрическая фигура, все точки которой расположены на одинаковом расстоянии от заданной точки, называется ....
2. Хорда, проходящая через центр окружности, называется ....
3. Все диаметры окружности ....
4. На рисунке 0(г) - окружность, В - точка касания прямой АВ и окружности. Прямая АВ называется ... к окружности.
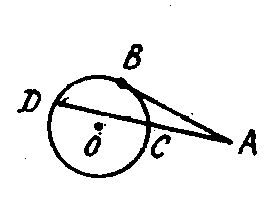
5. Прямая, имеющая с окружностью две общие точки, называется ... окружности.
6. Касательная к окружности и радиус, проведенный в точку касания, ....
7. На рисунке АВ - касательная, ОА - секущая, проходящая через центр окружности. Треугольник ОВА ... (вид треугольника).
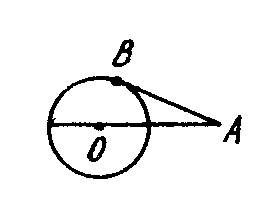
8. На рисунке ОС = СА, АВ - касательная к окружности с центром О. Угол ВАС равен ....
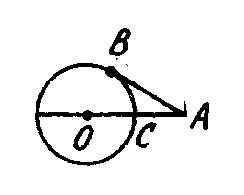
9. Хорды АВ и CD окружности пересекаются в точке К. Угол ADC равен углу ....
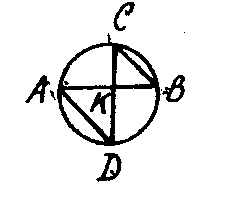
10. На рисунке О - центр окружности, угол СВА равен 40°. Дуга СmВ равна ....
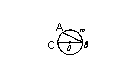
11. На рисунке AM = 15 см, MB = 4 см, MC = 3 см. Тогда DM = ... .
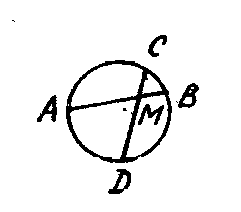
12*. На рисунке АВ = ВС, BD - высота треугольника АВС, ВК = 8 см, КС = 5 см. Тогда BD= ..., DC = ... .
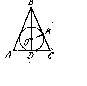
Карточки для индивидуальной работы.
Карточка 1.
1. Сколько общих точек могут иметь прямая и окружность? Сформулируйте свойство и признак касательной.
2. Отрезок BD - высота равнобедренного
треугольника AВС с основанием АС. На какие части окружность с
центром В и радиусом BD делит боковую сторону треугольника если
АВ=![]() см, BD=5 см?
см, BD=5 см?
3. На рисунке изображен прямоугольный треугольник AВС, стороны которого касаются окружности радиуса 1 см. На какие отрезки точка касания делит гипотенузу треугольника, равную 5 см?
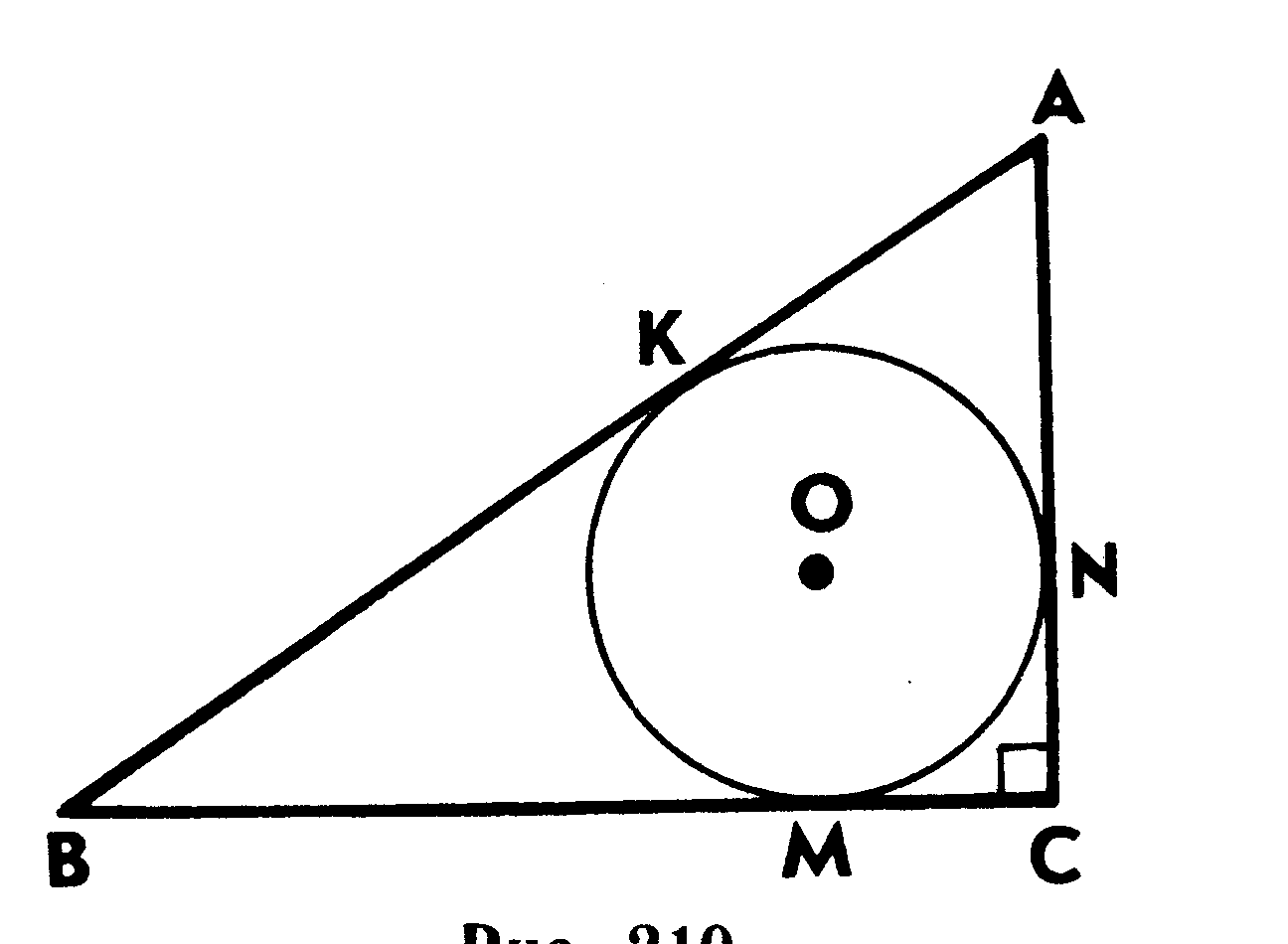
Карточка 2.
1. Какой угол называется вписанным? Сформулируйте теорему о вписанном угле.
2. Вершины треугольника со сторонами 2 см, 5 см и 6 см лежат на окружности. Докажите, что ни одна из сторон треугольника не является диаметром этой окружности.
3. На рисунке изображена окружность с центром О, АВ - касательная, а АС - секущая этой окружности. Найдите углы треугольника АВС, если BD=62°.
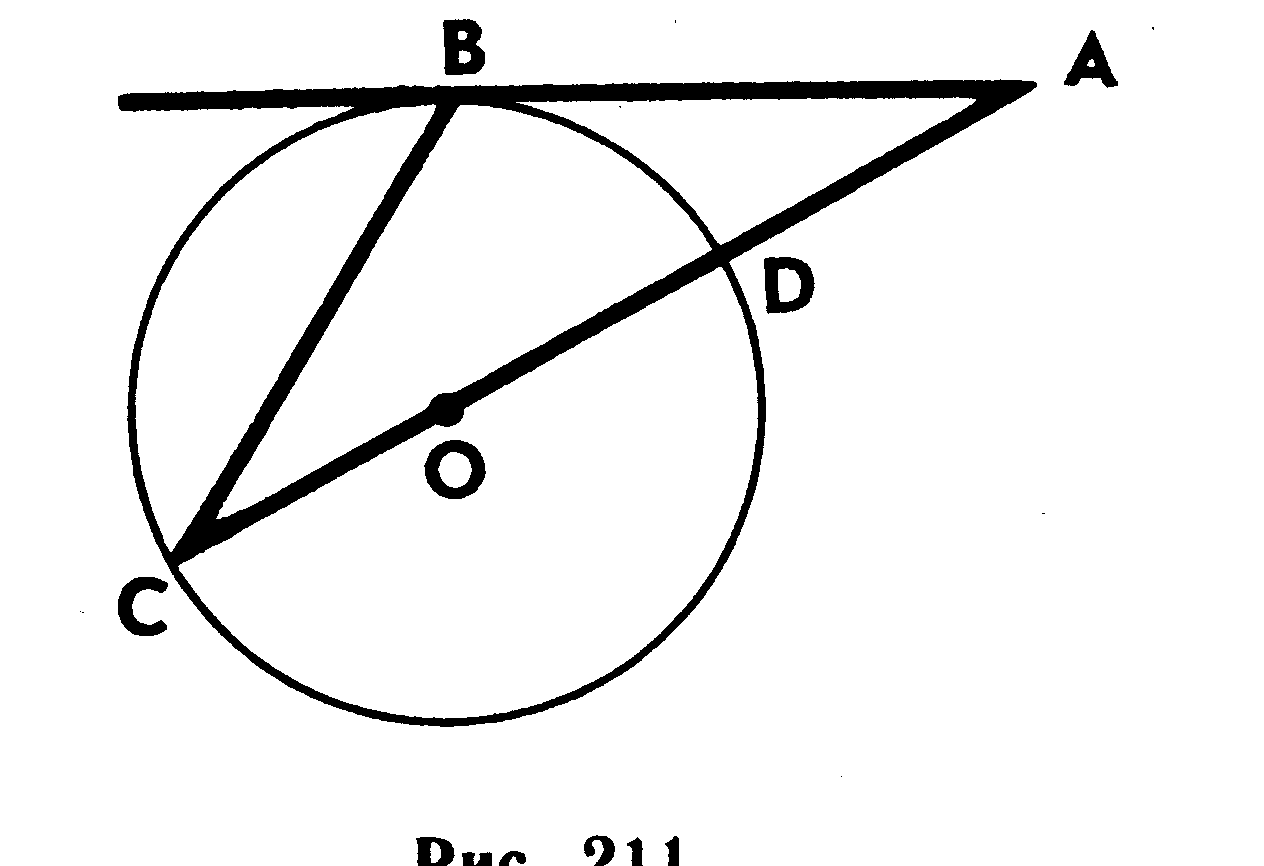
Карточка 3.
1. Сформулируйте теорему об отрезках пересекающихся хорд.
2. Хорды KL и MN окружности пересекаются в точке А. Найдите АК и AL, если АМ=2 дм, AN=6 дм, KL=7 дм.
3. На рисунке изображена окружность с центром О, АС - диаметр, а ВС - касательная к этой окружности. На какие части отрезок АВ делится точкой D, если АС=20 см, ВС=15 см?
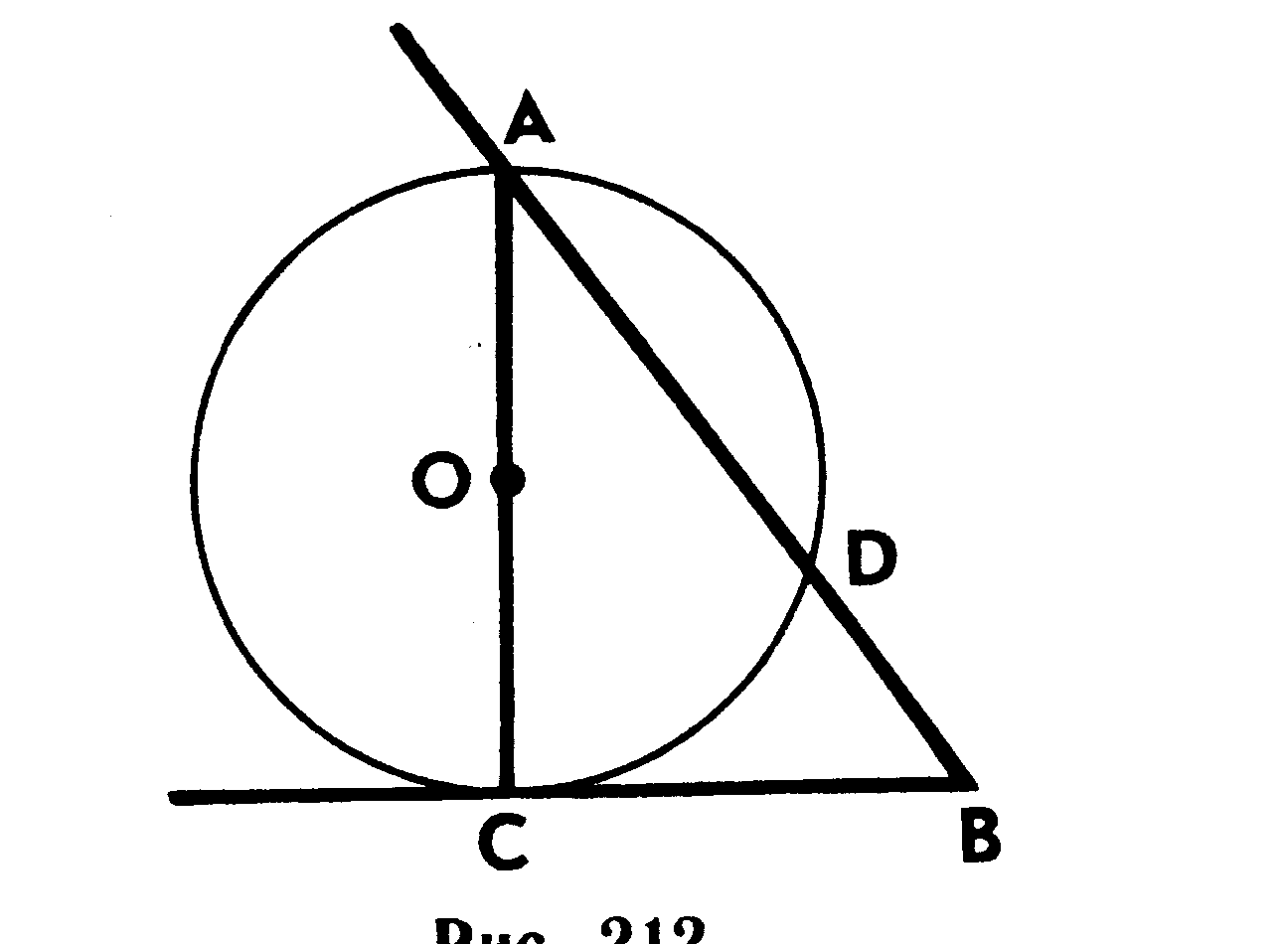
Карточка 4.
1. Сформулируйте теорему об окружности, вписанной в треугольник.
2. Впишите окружность в данный прямоугольный треугольник.
3. Основание равнобедренного треугольника равно 16 см, боковая сторона равна 17 см. Найдите радиус вписанной в этот треугольник окружности.
Карточка 5.
1. Сформулируйте утверждение о свойстве описанного четырехугольника. Верно ли обратное утверждение?
2. Найдите площадь прямоугольной трапеции, описанной около окружности, если боковые стороны этой трапеции равны 10 см и 16 см.
3. Площадь четырехугольника ABCD, описанного около окружности радиуса 5 дм, равна 90 дм2. Найдите стороны СD и AD этого четырехугольника, если AB=9 дм, ВС=10 дм.
Карточка 6.
1. Сформулируйте теорему об окружности, описанной около треугольника.
2. Постройте окружность, описанную около данного тупоугольного треугольника.
3. Найдите площадь равностороннего треугольника,
вписанного в окружность радиуса 4![]() см.
см.
Карточка 7.
1.Сформулируйте утверждение о свойстве вписанного четырехугольника. Верно ли обратное утверждение?
2. Площадь прямоугольника, вписанного в окружность, равна 48 см2. Найдите радиус окружности, если одна из сторон прямоугольника на 2 см больше другой.
3. На рисунке АМ и СМ - биссектрисы углов А и С треугольника АВС, AN и CN - биссектрисы внешних углов при вершинах A и С этого треугольника. Докажите, что около четырехугольника AMCN можно описать окружность.