- Учителю
- Рабочая программа по математике в 7 классе
Рабочая программа по математике в 7 классе
Муниципальное бюджетное
общеобразовательное учреждение
«Кривоозерская средняя общеобразовательная школа»
Рассмотрено Согласовано Утверждаю
Руководитель МО Заместитель Директор МБОУ
_______/ Седова И.А. / директора по УВР МБОУ «Кривоозерская СОШ»
Протокол №_____ от «Кривоозерская СОШ» _______/Воронина Н. Г./
«____»________2014г. ________/Коннова М.В./ Приказ №_____ от
«____»__________2014г. «____»_________2014г.
Рабочая программа
по математике в 7 классе
учителя математики
Седовой Ирины Анатольевны,
первой квалификационной категории.
Рассмотрено на
педагогическом совете №
от августа 2014 года
2014 - 2015 учебный год
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Рабочая программа по математике для 7 класса составлена на основании следующих нормативно-правовых документов:
1. Федерального Закона РФ «Об образовании в РФ» (от 29.12.2012 №273-Ф3);
2. Закона Республики Татарстан от 22.07.2013 N 68-ЗРТ «Об образовании» (принят ГС РТ
28.06.2013) (в действующей редакции);
3. Федерального компонента государственного стандарта основного общего образования
(утвержден Приказом МО и науки РФ от 05.03.2004 года №1089) (с действующими
изменениями);
4 . Примерной программы основного общего образования по математике;
5.Учебного плана МБОУ «Кривоозерская СОШ» на 2014-2015 учебный год;
6.Санитарно-эпидемиологических правил и нормативов (СанПиН 2.4.2. 2821-10 «Санитарно-эпидемиологические требования к условиям и организации обучения в общеобразовательных учреждениях» (зарегистрированными в Минюсте России 3 марта 2011 года, регистрационный №19993) ;
7. Приказа Министерства образования и науки Российской Федерации (Минобрнауки России) от 31 марта 2014 г. Москва № 253 «Об утверждении федерального перечня учебников, рекомендуемых к использованию при реализации имеющих государственную аккредитацию образовательных программ начального общего, основного общего, среднего общего образования»;
8. Положения о разработке рабочих программ учебных предметов, элективных курсов в МБОУ «Кривоозерская СОШ» Аксубаевского муниципального района Республики Татарстан. Протокол №1 от 29.08.2014года.
Уровень обучения - базовый.
Данная программа по математике для 7 класса составлена по учебникам для общеобразовательных учреждений: «Алгебра 7» Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова.-М. : Просвещение,2010; «Геометрия 7-9» Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев, Э. Г. Позняк, И. И. Юдина - М.: Просвещение,2003.
Согласно Федеральному базисному учебному плану на изучение математики в 7 классе отводится не менее 175 часов из расчета 5 ч в неделю, при этом структура изучения математики выстраивается блочно с чередованием учебного материала по алгебре и геометрии.
Формы промежуточной и итоговой аттестации:
Промежуточная аттестация проводится в форме тестов, контрольных, самостоятельных работ. Итоговая аттестация предусмотрена в виде административной контрольной работы.
Примерная программа конкретизирует содержание предметных тем образовательного стандарта и даёт примерное распределение учебных часов по разделам курса.
Цели изучения:
-
овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
-
интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясность и точность мысли, критичность мышления, интуиция, логическое мышление, элементы алгоритмической культуры, пространственных представлений, способность к преодолению трудностей;
-
формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
-
воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса;
-
развитие вычислительных и формально-оперативных алгебраических умений до уровня, позволяющего уверенно использовать их при решении задач математики и смежных предметов (физика, химия, основы информатики и вычислительной техники), усвоение аппарата уравнений и неравенств как основного средства математического моделирования прикладных задач, осуществление функциональной подготовки школьников. В ходе изучения курса учащиеся овладевают приёмами вычислений на калькуляторе.
Общая характеристика учебного предмета
Математическое образование в основной школе складывается из следующих содержательных компонентов (точные названия блоков): арифметика; алгебра; геометрия; элементы комбинаторики, теории вероятностей, статистики и логики. В своей совокупности они отражают богатый опыт обучения математике в нашей стране, учитывают современные тенденции отечественной и зарубежной школы и позволяют реализовать поставленные перед школьным образованием цели на информационноемком и практически значимом материале. Эти содержательные компоненты, развиваясь на протяжении всех лет обучения, естественным образом переплетаются и взаимодействуют в учебных курсах.
Арифметика призвана способствовать приобретению практических навыков, необходимых для повседневной жизни. Она служит базой для всего дальнейшего изучения математики, способствует логическому развитию и формированию умения пользоваться алгоритмами.
Алгебра. Изучение алгебры нацелено на формирование математического аппарата для решения задач из математики, смежных предметов, окружающей реальности. Язык алгебры подчеркивает значение математики как языка для построения математических моделей, процессов и явлений реального мира (одной из основных задач изучения алгебры является развитие алгоритмического мышления, необходимого, в частности, для освоения курса информатики; овладение навыками дедуктивных рассуждений. Преобразование символических форм вносит свой специфический вклад в развитие воображения, способностей к математическому творчеству. Другой важной задачей изучения алгебры является получение школьниками конкретных знаний о функциях как важнейшей математической модели для описания и исследования разнообразных процессов (равномерных, равноускоренных, экспоненциальных, периодических и др.), для формирования у обучающихся представлений о роли математики в развитии цивилизации и культуры.
Геометрия - один из важнейших компонентов математического образования, необходимый для приобретения конкретных знаний о пространстве и практически значимых умений, формирования языка описания объектов окружающего мира, для развития пространственного воображения и интуиции, математической культуры, для эстетического воспитания обучающихся. Изучение геометрии вносит вклад в развитие логического мышления, в формирование понятия доказательства.
Элементы логики, комбинаторики, статистики и теории вероятностей становятся обязательным компонентом школьного образования, усиливающим его прикладное и практическое значение. Этот материал необходим, прежде всего, для формирования функциональной грамотности - умений воспринимать и анализировать информацию, представленную в различных формах, понимать вероятностный характер многих реальных зависимостей, производить простейшие вероятностные расчёты. Изучение основ комбинаторики позволит учащемуся осуществлять рассмотрение случаев, перебор и подсчёт числа вариантов, в том числе в простейших прикладных задачах.
При изучении статистики и теории вероятностей обогащаются представления о современной картине мира и методах его исследования, формируется понимание роли статистики как источника социально значимой информации и закладываются основы вероятностного мышления.
Таким образом, в ходе освоения содержания курса учащиеся получают возможность:
развить представление о числе и роли вычислений в человеческой практике; сформировать практические навыки выполнения устных, письменных, инструментальных вычислений, развить вычислительную культуру;
овладеть символическим языком алгебры, выработать формально-оперативные алгебраические умения и научиться применять их к решению математических и нематематических задач;
изучить свойства и графики элементарных функций, научиться использовать функционально-графические представления для описания и анализа реальных зависимостей;
развить пространственные представления и изобразительные умения, освоить основные факты и методы планиметрии, познакомиться с простейшими пространственными телами и их свойствами;
получить представления о статистических закономерностях в реальном мире и о различных способах их изучения, об особенностях выводов и прогнозов, носящих вероятностный характер;
развить логическое мышление и речь - умения логически обосновывать суждения, проводить несложные систематизации, использовать различные языки математики (словесный, символический, графический) для иллюстрации, интерпретации, аргументации и доказательства;
сформировать представления об изучаемых понятиях и методах как важнейших средствах математического моделирования реальных процессов и явлений.
В курсе математики 7 класса систематизируются и обобщаются сведения о преобразованиях алгебраических выражений и решении уравнений с одной переменной; учащиеся знакомятся с важнейшими функциональными понятиями и с графиками прямой пропорциональности и линейной функции общего вида, действиями над степенями с натуральными показателями, формулами сокращенного умножения в преобразованиях целых выражений в многочлены и в разложении многочленов на множители, со способами решения систем линейных уравнений с двумя переменными, вырабатывается умение решать системы уравнений и применять их при решении текстовых задач.
Примечание.
Количество часов по темам может быть изменено в связи с уплотнением материала, исходя из опыта преподавания и с учетом непредвиденных обстоятельств.
Содержание учебного предмета
Алгебра
Выражения, тождества, уравнения
Числовые выражения с переменными. Простейшие преобразования выражений. Уравнение, корень уравнения. Линейное уравнение с одной переменной. Решение текстовых задач методом составления уравнений. Статистические характеристики
Функции
Функция, область определения функции. Вычисление значений функции по формуле. График функции. Прямая пропорциональность и ее график. Линейная функция и её график.
Степень с натуральным показателем
Степень с натуральным показателем и ее свойства. Одночлен. Функции у=х2, у=х3 и их графики.
Многочлены
Многочлен. Сложение, вычитание и умножение многочленов. Разложение многочленов на множители
Формулы сокращенного умножения
Формулы (а - b )(а + b ) = а2 - b 2, (а ± b)2 = а2± 2а b + b2, (а ± b)3 = а3 ± За2b + За b2 ± b3, (а ± b) (а2 ![]() а b + b2) = а3 ± b3. Применение формул сокращённого умножения в преобразованиях выражений
а b + b2) = а3 ± b3. Применение формул сокращённого умножения в преобразованиях выражений
Системы линейных уравнений
Система уравнений. Решение системы двух линейных уравнений с двумя переменными и его геометрическая интерпретация. Решение текстовых задач методом составления систем уравнений
Элементы логики, комбинаторики, статистики и теории вероятностей
Геометрия
Начальные геометрические сведения
Простейшие геометрические фигуры: прямая, точка, отрезок, луч, угол. Понятие равенства геометрических фигур. Сравнение отрезков и углов. Измерение отрезков, длина отрезка. Измерение углов, градусная мера угла. Смежные и вертикальные углы, их свойства. Перпендикулярные прямые
Треугольники
Треугольник. Признаки равенства треугольников. Перпендикуляр к прямой. Медианы, биссектрисы и высоты треугольника. Равнобедренный треугольник и его свойства. Задачи на построение с помощью циркуля и линейки
Параллельные прямые
Признаки параллельности прямых. Аксиома параллельных прямых. Свойства параллельных прямых
Соотношения между сторонами и углами треугольника
Сумма углов треугольника. Соотношение между сторонами и углами треугольника. Неравенство треугольника. Прямоугольные треугольники, их свойства и признаки равенства. Расстояние от точки до прямой. Расстояние между параллельными прямыми. Построение треугольника по трем элементам
Выражения, тождества, уравнения. Статистика
Числовые выражения с переменными. Простейшие преобразования выражений. Уравнение, корень уравнения. Линейное уравнение с одной переменной. Решение текстовых задач методом составления уравнений. Статистические характеристики.
Цель: систематизировать и обобщить сведения о преобразованиях алгебраических выражений и решении уравнений с одной переменной.
Первая тема курса 7 класса является связующим звеном между курсом математики 5-6 классов и курсом алгебры. В ней закрепляются вычислительные навыки, систематизируются и обобщаются сведения о преобразованиях выражений и решении уравнений.
Нахождение значений числовых и буквенных выражений даёт возможность повторить с обучающимися правила действий с рациональными числами. Умения выполнять арифметические действия с рациональными числами являются опорными для всего курса алгебры. Следует выяснить, насколько прочно овладели ими учащиеся, и в случае необходимости организовать повторение с целью ликвидации выявленных пробелов. Развитию навыков вычислений должно уделяться серьезное внимание и в дальнейшем при изучении других тем курса алгебры.
В связи с рассмотрением вопроса о сравнении значений выражений расширяются сведения о неравенствах: вводятся знаки ≥ и ≤, дается понятие о двойных неравенствах.
При рассмотрении преобразований выражений формально-оперативные умения остаются на том же уровне, учащиеся поднимаются на новую ступень в овладении теорией. Вводятся понятия «тождественно равные выражения», «тождество», «тождественное преобразование выражений», содержание которых будет постоянно раскрываться и углубляться при изучении преобразований различных алгебраических выражений. Подчеркивается, что основу тождественных преобразований составляют свойства действий над числами.
Усиливается роль теоретических сведений при рассмотрении уравнений. С целью обеспечения осознанного восприятия обучающимися алгоритмов решения уравнений вводится вспомогательное понятие равносильности уравнений, формулируются и разъясняются на конкретных примерах свойства равносильности. Дается понятие линейного уравнения и исследуется вопрос о числе его корней. В системе упражнений особое внимание уделяется решению уравнений вида ах=b при различных значениях а и b. Продолжается работа по формированию у обучающихся умения использовать аппарат уравнений как средство для решения текстовых задач. Уровень сложности задач здесь остается таким же, как в 6 классе.
Изучение темы завершается ознакомлением обучающихся с простейшими статистическими характеристиками: средним арифметическим, модой, медианой, размахом. Учащиеся должны уметь пользовать эти характеристики для анализа ряда данных в несложных ситуациях.
Функции
Функция, область определения функции. Вычисление значений функции по формуле. График функции. Прямая пропорциональность и ее график. Линейная функция и её график.
Цель: ознакомить обучающихся с важнейшими функциональными понятиями и с графиками прямой пропорциональности и линейной функции общего вида.
Данная тема является начальным этапом в систематической функциональной подготовке обучающихся. Здесь вводятся такие понятия, как функция, аргумент, область определения функции, график функции. Функция трактуется как зависимость одной переменной от другой. Учащиеся получают первое представление о способах задания функции. В данной теме начинается работа по формированию у обучающихся умений находить по формуле значение функции по известному значению аргумента, выполнять ту же задачу по графику и решать по графику обратную задачу. Функциональные понятия получают свою конкретизацию при изучении линейной функции и ее частного вида - прямой пропорциональности. Умения строить и читать графики этих функций широко используются как в самом курсе алгебры, так и в курсах геометрии и физики. Учащиеся должны понимать, как влияет знак коэффициента на расположение в координатной плоскости графика функции у=кх, где к![]() 0, как зависит от значений к и b взаимное расположение графиков двух функций вида у=кх+b.
0, как зависит от значений к и b взаимное расположение графиков двух функций вида у=кх+b.
Формирование всех функциональных понятий и выработка соответствующих навыков, а также изучение конкретных функций сопровождаются рассмотрением примеров реальных зависимостей между величинами, что способствует усилению прикладной направленности курса алгебры.
Степень с натуральным показателем
Степень с натуральным показателем и ее свойства. Одночлен. Функции у=х2, у=х3 и их графики.
Цель: выработать умение выполнять действия над степенями с натуральными показателями.
В данной теме дается определение степени с натуральным показателем. В курсе математики 6 класса учащиеся уже встречались с примерами возведения чисел в степень. В связи с вычислением значений степени в 7 классе дается представление о нахождении значений степени с помощью калькулятора; Рассматриваются свойства степени с натуральным показателем: На примере доказательства свойств аm · аn = аm+n; аm : аn = аm-n, где m > n; (аm)n = аm·n; (ab)m = ambm учащиеся впервые знакомятся с доказательствами, проводимыми на алгебраическом материале. Указанные свойства степени с натуральным показателем находят применение при умножении одночленов и возведении одночленов в степень. При нахождении значений выражений содержащих степени, особое внимание следует обратить на порядок действий.
Рассмотрение функций у=х2, у=х3 позволяет продолжить работу по формированию умений строить и читать графики функций. Важно обратить внимание обучающихся на особенности графика функции у=х2:график проходит через начало координат, ось Оу является его осью симметрии, график расположен в верхней полуплоскости.
Умение строить графики функций у=х2 и у=х3 используется для ознакомления обучающихся с графическим способом решения уравнений.
Начальные геометрические сведения
Простейшие геометрические фигуры: прямая, точка, отрезок, луч, угол. Понятие равенства геометрических фигур. Сравнение отрезков и углов. Измерение отрезков, длина отрезка. Измерение углов, градусная мера угла. Смежные и вертикальные углы, их свойства. Перпендикулярные прямые.
Цель: систематизировать знания обучающихся о простейших геометрических фигурах и их свойствах; ввести понятие равенства фигур.
В данной теме вводятся основные геометрические понятия и свойства простейших геометрических фигур на основе наглядных представлений обучающихся путем обобщения очевидных или известных из курса математики I- 6 классов геометрических фактов. Понятие аксиомы на начальном этапе обучения не вводится, и сами аксиомы не формулируются в явном виде. Необходимые исходные положения, на основе которых изучаются свойства геометрических фигур, приводятся в описательной форме. Принципиальным моментом данной темы является введение понятия равенства геометрических фигур на основе наглядного понятия наложения. Определенное внимание должно уделяться практическим приложениям геометрических понятий
Многочлены
Многочлен. Сложение, вычитание и умножение многочленов. Разложение многочленов на множители.
Цель: выработать умение выполнять сложение, вычитание, умножение многочленов и разложение многочленов на множители.
Данная тема играет фундаментальную роль в формировании умения выполнять тождественные преобразования алгебраических выражений. Формируемые здесь формально-оперативные умения являются опорными при изучении действий с рациональными дробями, корнями, степенями с рациональными показателями.
Изучение темы начинается с введения понятий многочлена, стандартного вида многочлена, степени многочлена. Основное место в этой теме занимают алгоритмы действий с многочленами - сложение, вычитание и умножение. Учащиеся должны понимать, что сумму, разность, произведение многочленов всегда можно представить в виде многочлена. Действия сложения, вычитания и умножения многочленов выступают как составной компонент в заданиях на преобразования целых выражений. Поэтому нецелесообразно переходить к комбинированным заданиям прежде, чем усвоены основные алгоритмы.
Серьезное внимание в этой теме уделяется разложению многочленов на множители с помощью вынесения за скобки общего множителя и с помощью группировки. Соответствующие преобразования находят широкое применение как в курсе 7 класса, так и в последующих курсах, особенно в действиях с рациональными дробями.
В данной теме учащиеся встречаются с примерами использования рассматриваемых преобразований при решении разнообразных задач, в частности при решении уравнений. Это позволяет в ходе изучения темы продолжить работу по формированию умения решать уравнения, а также решать задачи методом составления уравнений. В число упражнений включаются несложные задания на доказательство тождества.
Треугольники
Треугольник. Признаки равенства треугольников. Перпендикуляр к прямой. Медианы, биссектрисы и высоты треугольника. Равнобедренный треугольник и его свойства. Задачи на построение с помощью циркуля и линейки.
Цель: ввести понятие теоремы; выработать умение доказывать равенство треугольников с помощью изученных признаков; ввести новый класс задач - на построение с помощью циркуля и линейки.
Признаки равенства треугольников являются основным рабочим аппаратом всего курса геометрии. Доказательство большей части теорем курса и также решение многих задач проводится по следующей схеме: поиск равных треугольников - обоснование их равенства с помощью какого-то признака - следствия, вытекающие из равенства треугольников.
Применение признаков равенства треугольников при решении задач дает возможность постепенно накапливать опыт проведения доказательных рассуждений. На начальном этапе изучения и применения признаков равенства треугольников целесообразно использовать задачи с готовыми чертежами
Формулы сокращенного умножения
Формулы (а - b )(а + b ) = а2 - b 2, (а ± b)2 = а2± 2а b + b2, (а ± b)3 = а3 ± За2b + За b2 ± b3, (а ± b) (а2 ![]() а b + b2) = а3 ± b3. Применение формул сокращённого умножения в преобразованиях выражений.
а b + b2) = а3 ± b3. Применение формул сокращённого умножения в преобразованиях выражений.
Цель: выработать умение применять формулы сокращенного умножения в преобразованиях целых выражений в многочлены и в разложении многочленов на множители.
В данной теме продолжается работа по формированию у обучающихся умения выполнять тождественные преобразования целых выражений. Основное внимание в теме уделяется формулам (а - b)(а + b) = а2 - b 2, (а ± b)2 = а2± 2а b + b2. Учащиеся должны знать эти формулы и соответствующие словесные формулировки, уметь применять их как «слева направо», так и «справа налево». Наряду с указанными рассматриваются также формулы (а ± b)3 = а3 ± За2b + За b2 ± b3, (а ± b) (а2 ![]() а b + b2) = а3 ± b3. Однако они находят меньшее применение в курсе, поэтому не следует излишне увлекаться выполнением упражнений на их использование.
а b + b2) = а3 ± b3. Однако они находят меньшее применение в курсе, поэтому не следует излишне увлекаться выполнением упражнений на их использование.
В заключительной части темы рассматривается применение различных приемов разложения многочленов на множители, а также использование преобразований целых выражений для решения широкого круга задач.
Параллельные прямые
Признаки параллельности прямых. Аксиома параллельных прямых. Свойства параллельных прямых.
Цель: ввести одно из важнейших понятий - понятие параллельных прямых; дать первое представление об аксиомах и аксиоматическом методе в геометрии; ввести аксиому параллельных прямых.
Признаки и свойства параллельных прямых, связанные с углами, образованными при пересечении двух прямых секущей (накрест лежащими, односторонними, соответственными), широко используются в дальнейшем при изучении четырехугольников, подобных треугольников, при решении задач, а также в курсе стереометрии.
Системы линейных уравнений
Система уравнений. Решение системы двух линейных уравнений с двумя переменными и его геометрическая интерпретация. Решение текстовых задач методом составления систем уравнений.
Цель: ознакомить обучающихся со способом решения систем линейных уравнений с двумя переменными, выработать умение решать системы уравнений и применять их при решении текстовых задач.
Изучение систем уравнений распределяется между курсами 7 и 9 классов. В 7 классе вводится понятие системы и рассматриваются системы линейных уравнений.
Изложение начинается с введения понятия «линейное уравнение с двумя переменными». В систему упражнений включаются несложные задания на решение линейных уравнений с двумя переменными в целых числах.
Формируется умение строить график уравнения ах + bу=с, где а≠0 или b≠0, при различных значениях а, b, с. Введение графических образов даёт возможность наглядно исследовать вопрос о числе решений системы двух линейных уравнений с двумя переменными. Основное место в данной теме занимает изучение алгоритмов решения систем двух линейных уравнений с двумя переменными способом подстановки и способом сложения. Введение систем позволяет значительно расширить круг текстовых задач, решаемых с помощью аппарата алгебры. Применение систем упрощает процесс перевода данных задачи с обычного языка на язык уравнений.
Соотношения между сторонами и углами треугольника
Сумма углов треугольника. Соотношение между сторонами и углами треугольника. Неравенство треугольника. Прямоугольные треугольники, их свойства и признаки равенства. Расстояние от точки до прямой. Расстояние между параллельными прямыми. Построение треугольника по трем элементам.
Цель: рассмотреть новые интересные и важные свойства треугольников.
В данной теме доказывается одна из важнейших теорем геометрии - теорема о сумме углов треугольника. Она позволяет дать классификацию треугольников по углам (остроугольный, прямоугольный, тупоугольный), а также установить некоторые свойства и признаки равенства прямоугольных треугольников.
Понятие расстояния между параллельными прямыми вводится на основе доказанной предварительно теоремы о том, что все точки каждой из двух параллельных прямых равноудалены от другой прямой. Это понятие играет важную роль, и частности используется в задачах на построение.
При решении задач на построение в 7 классе следует ограничиться только выполнением и описанием построения искомой фигуры. В отдельных случаях можно провести устно анализ и доказательство, а элементы исследования должны присутствовать лишь тогда, когда это оговорено условием задачи
Элементы логики, комбинаторики, статистики и теории вероятностей
На этом этапе продолжается решение задач путем перебора возможных вариантов, изучается статистический подход к понятию вероятности. Дается классическое определение вероятности, формируются умения вычислять вероятности с помощью формул комбинаторики. Особое внимание уделяется правилу сложения вероятностей.
Повторение. Решение задач.
Цель: Повторение, обобщение и систематизация знаний, умений и навыков за курс геометрии 7 класса.
Учебно - тематическое планирование
№
Тема
Кол-во часов при
5 ч в неделю
Кол-во контрольных работ
Административная
контрольная работа
1
Повторение курса математики 6 класса
2
2
Выражения .тождества. уравнения .
19
3
3
Элементы статистики и теории вероятностей
5
4
Функции
14
1
5
Степень с натуральным показателем
14
1
6
Начальные игеометрические сведения
9
1
7
Многочлены
20
1
1
8
Треугольники
15
1
9
Формулы сокращенного умножения.
20
2
10
Параллельные прямые
9
1
11
Системы линейных уравнений
16
1
12
Соотношения между сторонами и углами треугольника
16
2
13
Итоговое повторение курса математики 7 класса
16
1
Итого
175
16
2
Требования к уровню подготовки обучающихся в 7 классе
В результате изучения обучающиеся должны:
знать/понимать
-
существо понятия математического доказательства; примеры доказательств;
-
существо понятия алгоритма; примеры алгоритмов;
-
как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;
-
как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;
-
как потребности практики привели математическую науку к необходимости расширения понятия числа;
-
вероятностный характер многих закономерностей окружающего мира; примеры статистических закономерностей и выводов;
-
каким образом геометрия возникла из практических задач землемерия; примеры геометрических объектов и утверждений о них, важных для практики;
-
смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации;
уметь
-
выполнять устно арифметические действия: сложение и вычитание двузначных чисел и десятичных дробей с двумя знаками, умножение однозначных чисел, арифметические операции с обыкновенными дробями с однозначным знаменателем и числителем;
-
переходить от одной формы записи чисел к другой, представлять десятичную дробь в виде обыкновенной и в простейших случаях обыкновенную в виде десятичной, проценты - в виде дроби и дробь - в виде процентов; записывать большие и малые числа с использованием целых степеней десятки;
-
выполнять арифметические действия с рациональными числами, сравнивать рациональные и действительные числа; находить в несложных случаях значения степеней с целыми показателями и корней; находить значения числовых выражений;
-
округлять целые числа и десятичные дроби, находить приближения чисел с недостатком и с избытком, выполнять оценку числовых выражений;
-
пользоваться основными единицами длины, массы, времени, скорости, площади, объема; выражать более крупные единицы через более мелкие и наоборот;
-
решать текстовые задачи, включая задачи, связанные с отношением и с пропорциональностью величин, дробями и процентами;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
-
решения несложных практических расчетных задач, в том числе c использованием при необходимости справочных материалов, калькулятора, компьютера;
-
устной прикидки и оценки результата вычислений; проверки результата вычисления с использованием различных приемов;
-
интерпретации результатов решения задач с учетом ограничений, связанных с реальными свойствами рассматриваемых процессов и явлений;
уметь
-
составлять буквенные выражения и формулы по условиям задач; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, осуществлять подстановку одного выражения в другое; выражать из формул одну переменную через остальные;
-
выполнять основные действия со степенями с натуральными показателями, с многочленами; выполнять разложение многочленов на множители; выполнять тождественные преобразования рациональных выражений;
-
решать линейные уравнения решать линейные решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи;
-
изображать числа точками на координатной прямой;
-
определять координаты точки плоскости, строить точки с заданными координатами;
-
находить значения функции, заданной формулой, таблицей, графиком по ее аргументу; находить значение аргумента по значению функции, заданной графиком или таблицей;
-
применять графические представления при решении уравнений, систем, неравенств;
-
описывать свойства изученных функций (у=кх, где к
 0, у=кх+b, у=х2, у=х3), строить их графики.
0, у=кх+b, у=х2, у=х3), строить их графики.
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
-
выполнения расчетов по формулам, составления формул, выражающих зависимости между реальными величинами; нахождения нужной формулы в справочных материалах;
-
моделирования практических ситуаций и исследовании построенных моделей с использованием аппарата алгебры;
-
описания зависимостей между физическими величинами соответствующими формулами при исследовании несложных практических ситуаций;
-
интерпретации графиков реальных зависимостей между величинами.
уметь
-
проводить несложные доказательства, получать простейшие следствия из известных или ранее полученных утверждений, оценивать логическую правильность рассуждений, использовать примеры для иллюстрации и контрпримеры для опровержения утверждений;
-
решать комбинаторные задачи путем систематического перебора возможных вариантов, вычислять средние значения результатов измерений;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
-
выстраивания аргументации при доказательстве (в форме монолога и диалога);
-
распознавания логически некорректных рассуждений;
-
записи математических утверждений, доказательств;
-
анализа реальных числовых данных, представленных в виде диаграмм, графиков, таблиц;
-
решения практических задач в повседневной и профессиональной деятельности с использованием действий с числами, процентов, длин, площадей, объемов, времени, скорости;
-
решения учебных и практических задач, требующих систематического перебора вариантов;
-
понимания статистических утверждений.
уметь
-
пользоваться языком геометрии для описания предметов окружающего мира;
-
распознавать геометрические фигуры, различать их взаимное расположение;
-
изображать геометрические фигуры; выполнять чертежи по условию задач; осуществлять преобразования фигур;
-
вычислять значения геометрических величин (длин, углов, площадей, объемов), находить стороны, углы и площади треугольников, длины ломаных, дуг окружности, площадей основных геометрических фигур и фигур, составленных из них;
-
решать геометрические задачи, опираясь на изученные свойства фигур и отношений между ними, применяя дополнительные построения, алгебраический аппарат, идеи симметрии;
-
проводить доказательные рассуждения при решении задач, используя известные теоремы, обнаруживая возможности для их использования;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
-
описания реальных ситуаций на языке геометрии;
-
расчетов, включающих простейшие формулы;
-
решения практических задач, связанных с нахождением геометрических величин (используя при необходимости справочники и технические средства);
-
построений геометрическими инструментами (линейка, угольник, циркуль, транспортир).
Учебно-тематическое планирование по математике в 7 классе.
№
Тема
урока
Кол-во
часов
Дата проведения
Примечание
Повторение изученного в 6 классе (2ч)
1
Действия с обыкновенными дробями. Нахождение дроби от числа и числа по его дроби
1
1.09.2014
2
Действия с рациональными числами. Решение уравнений.
1
2
Выражения, тождества, уравнения (19ч)
3
Числовые выражения
2
3
4
Числовые выражения Решение задач по теме
4
5
Выражения с переменными
2
6
6
Выражения с переменными. Решение задч
8
7
Сравнения значений выражений
1
9
8
Свойства действий над числами. Вводная контрольная работа.
2
10
9
11
10
Тождества. Тождественные преобразования выражений
3
13
11
15
12
16
13
Контрольная работа № 1 « Выражения, тождества»
1
17
14
Уравнения и его корни
1
18
15
Линейное уравнение с одной переменной
3
20
16
22
17
23
18
Решение задач с помощью уравнений
3
24
19
25
20
27
21
Контрольная работа № 2 « Уравнения»
1
29
Элементы статистики и теории вероятностей (5ч)
22
Статистические характеристики
5
30
1.10
23
24
2
25
6
26
7
Функции(14ч)
27
Что такое функция
1
8
28
Вычисление значений функции по формуле
2
9
29
11
30
График функции
3
13
31
14
32
15
33
Линейная функция и ее график
3
16
34
18
35
20
36
Прямая пропорциональность
2
21
37
22
38
Линейная функция и ее график Прямая пропорциональность.
2
23
39
25
40
Контрольная работа
№ 3 « Функции»
1
27
Степень с натуральным показателем(14ч)
41
Определение степени с натуральным показателем
2
28
42
29
43
Умножение и деление степеней
2
30
44
1.11
45
Возведение в степень произведения и степени
2
10
46
11
47
Одночлен и его стандартный вид
1
12
48
Умножение одночленов Возведение одночлена в степень
3
13
49
15
50
17
51
Функция у=х2 и у=х3 и их графики
2
18
52
19
53
Абсолютная и относительная погрешности
1
20
54
Контрольная работа № 4
« Степень с натуральным показателем»
1
22
55
Прямая и отрезок. Луч и угол.
1
24
56
Сравнение отрезков и углов.
2
25
57
26
58
Измерение отрезков
1
27
59
Измерение углов.
2
29
60
1.12
61
Перпендикулярные прямые.
1
2
62
Обобщение. Решение задач
1
3
63
Контрольная работа №5 « Начальные геометрические сведения»
1
4
Многочлены (20ч)
64
Многочлен и его стандартный вид
1
6
65
Сложение и вычитание многочленов
2
8
66
9
67
Умножение одночлена на многочлен
3
10
68
11
69
13
70
Вынесение общего множителя за скобки
3
15
71
16
72
17
73
АК Контрольная работа
№ 6 « Сложение и вычитание многочленов»
1
18
74
Умножение многочлена на многочлен
3
20
75
22
76
23
77
Разложение многочлена на множители способом группировки
4
24
78
25
79
27
80
12.01.2015
81
Доказательство тождеств
2
13
82
14
83
Контрольная работа
№ 7 « Разложение многочлена на множители способом группировки»
1
15
Треугольники(15ч)
84
Первый признак равенства треугольников.
3
17
85
19
86
20
87
Медианы, биссектрисы и высоты треугольников.
3
21
88
22
89
24
90
Второй и третий признаки равенства треугольников.
4
26
91
27
92
28
93
29
94
Задачи на построение.
2
31
95
2.02
96
Обобщение. Решение задач
2
3
97
4
98
Контрольная работа №8 «Треугольники»
1
5
Формулы сокращенного умножения (20ч)
99
Возведение в квадрат и куб суммы и разности двух выражений
2
7
100
9
101
Разложение на множители с помощью формул квадрата суммы и квадрата разности
2
10
102
11
103
Умножение разности двух выражений на их сумму
2
12
104
14
105
Разложение разности квадратов на множители
3
16
106
17
107
18
108
Разложение на множители суммы и разности кубов
1
19
109
Разложение на множители суммы и разности кубов
1
21
110
Контрольная работа № 9 « Формулы сокращенного умножения»
1
23
111
Преобразование целого выражения в многочлен
2
24
112
25
113
Применение различных способов для разложения на множители
3
26
114
28
115
2.03
116
Применение преобразований целых выражений
2
3
117
4
118
Контрольная работа № 10
« Применение различных способов для разложения на множители»
1
5
Параллельные прямые (9ч)
119
Признаки параллельности двух прямых.
2
7
120
9
121
Аксиома параллельных прямых
3
10
122
11
123
12
124
Обобщение. Решение задач.
3
14
125
16
126
17
127
Контрольная работа №11. « Параллельные прямые»
1
18
Системы линейных уравнений (16ч)
128
Линейное уравнение с двумя переменными
2
19
129
21
130
График линейного уравнения с двумя переменными
2
1.04
131
2
132
Системы линейных уравнений с двумя переменными
2
4
133
6
134
Способ подстановки
3
7
135
8
136
9
137
Способ сложения
2
11
138
13
139
Решение задач с помощью систем уравнений
4
14
140
15
141
16
142
18
143
Контрольная работа
№ 12 « Системы линейных уравнений»
1
20
Соотношения между сторонами и углами треугольника (16ч)
144
Сумма углов треугольника
2
21
145
22
146
Соотношение между сторонами и углами
треугольника.
2
23
147
25
27
148
Контрольная работа №13. « Соотношение между сторонами и углами
треугольника»
1
28
149
Прямоугольные треугольники.
2
29
150
30
151
Построение треугольника по трём элементам.
3
2.05
152,153
4
154
Обобщение. Решение задач.
2
5
155
6
156
Контрольная работа №14. « Построение треугольника по трём элементам.»
1
7
157
Повторение. Решение задач
3
9
158
11
12
159
Итоговое повторение курса математики 7 класса (16ч)
160
Итоговое повторение. Выражения, тождества, уравнения
1
13
161
Итоговое повторение. Функции
1
14
162
Итоговое повторение. Степень с натуральным показателем
1
16
163
Итоговое повторение. Начальные сведения
1
18
164
Итоговое повторение. Многочлены
1
19
165
Итоговое повторение. Треугольники
2
20
166
21
167
Итоговое повторение. Формулы сокращенного умножения
2
23
168
23
упл
169
Итоговое повторение. Параллельные прямые
1
25
170
Итоговое повторение. Системы линейных уравнений
1
26
171
Итоговое повторение. Соотношения между сторонами и углами треугольника
1
27
172
Итоговое повторение
2
27
упл
173
27
упл
174
Итоговая контрольная работа
2
28
175
30
Нормы оценки знаний, умений и компетентностей учащихся 7 класса по математике
1. Оценка письменных контрольных работ.
Ответ оценивается отметкой «5», если:
-
работа выполнена полностью;
-
в логических рассуждениях и обосновании решения нет пробелов и ошибок;
-
в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).
Отметка «4» ставится в следующих случаях:
-
работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);
-
допущены одна ошибка или есть два - три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).
Отметка «3» ставится, если:
-
допущено более одной ошибки или более двух - трех недочетов в выкладках, чертежах или графиках, но обучающийся обладает обязательными умениями по проверяемой теме.
Отметка «2» ставится, если:
-
допущены существенные ошибки, показавшие, что обучающийся не обладает обязательными умениями по данной теме в полной мере.
Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии обучающегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные обучающемуся дополнительно после выполнения им каких-либо других заданий.
2. Оценка устных ответов.
Ответ оценивается отметкой «5», если ученик:
-
полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;
-
изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;
-
правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;
-
показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;
-
продемонстрировал знание теории ранее изученных сопутствующих тем, сформированность и устойчивость используемых при ответе умений и навыков;
-
отвечал самостоятельно, без наводящих вопросов учителя;
-
возможны одна - две неточности при освещение второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя.
Ответ оценивается отметкой «4», если удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:
-
в изложении допущены небольшие пробелы, не исказившее математическое содержание ответа;
-
допущены один - два недочета при освещении основного содержания ответа, исправленные после замечания учителя;
-
допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.
Отметка «3» ставится в следующих случаях:
-
неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для усвоения программного материала;
-
имелись затруднения или допущены ошибки в определении математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;
-
ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;
-
при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.
Отметка «2» ставится в следующих случаях:
-
не раскрыто основное содержание учебного материала;
-
обнаружено незнание учеником большей или наиболее важной части учебного материала;
-
допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.
Общая классификация ошибок
При оценке знаний, умений и навыков обучающихся следует учитывать все ошибки (грубые и негрубые) и недочёты.
3.1. Грубыми считаются ошибки:
-
незнание определения основных понятий, законов, правил, основных положений теории, незнание формул, общепринятых символов обозначений величин, единиц их измерения;
-
незнание наименований единиц измерения;
-
неумение выделить в ответе главное;
-
неумение применять знания, алгоритмы для решения задач;
-
неумение делать выводы и обобщения;
-
неумение читать и строить графики;
-
неумение пользоваться первоисточниками, учебником и справочниками;
-
потеря корня или сохранение постороннего корня;
-
отбрасывание без объяснений одного из них;
-
равнозначные им ошибки;
-
вычислительные ошибки, если они не являются опиской;
-
логические ошибки.
3.2. К негрубым ошибкам следует отнести:
-
неточность формулировок, определений, понятий, теорий, вызванная неполнотой охвата основных признаков определяемого понятия или заменой одного - двух из этих признаков второстепенными;
-
неточность графика;
-
нерациональный метод решения задачи или недостаточно продуманный план ответа (нарушение логики, подмена отдельных основных вопросов второстепенными);
-
нерациональные методы работы со справочной и другой литературой;
-
неумение решать задачи, выполнять задания в общем виде.
3.3. Недочетами являются:
-
нерациональные приемы вычислений и преобразований;
-
небрежное выполнение записей, чертежей, схем, графиков.
Список литературы.
-
Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Пешков, С.В. Суворова. Под редакцией С.А. Теляковского. Алгебра, 7 класс, -М.:Просвещение, 2010.
-
Атанасян Л.С., Бутузов В.Ф. и др. Геометрия, 7-9, -М.: Просвещение, 2003.
-
Газета «Математика», №11, 2006 г. Приложение к газете «Первое сентября» Тематическое планирование и контрольные работы
-
Звавич Л.И., Кузнецова Л.В., Суворова С.Б. Дидактические материалы для 7 класса - М.: Просвещение, 2000
-
Ершова А.П., Голобородько В.В., Ершова А.С. Самостоятельные и контрольные работы по алгебре и геометрии для 7 класса, - М.: Илекса, 2010.
-
Геометрия 7-9 классы. Задачи и упражнения на готовых чертежах. Рабинович.Е.М.,-М.: ИЛЕКСА, 2013
График контрольных работ по математике в 7 классе.
Учитель Седова И.А.
№
Тема
Кол-во часов при
5 ч в неделю
Кол-во контрольных работ
Дата
1.
Повторение
2
Вводная контрольная
9.09.14
1.
Выражения ,тождества, уравнения .
19
2
17.09.14
29.09.14
Статистика
5
2
Функции
14
1
27.10.14
3
Степень с натуральным показателем
14
1
22.11.14
4
Начальные игеометрические сведения
9
1
4.12.14
5
Многочлены
20
АК, 1
18.12.14
15.01.15
6
Треугольники
15
1
5.02.15
7
Формулы сокращенного умножения.
20
2
23.02.15
5.03.15
8
Параллельные прямые
9
1
18.03.15
9
Системы линейных уравнений
16
1
20.04.15
10
Соотношения между сторонами и углами треугольника
16
2
27.04.15
7.05.15
11
Итоговое повторение курса математики 7 класса
16
АК
28.05
Итого
175
16
АК- административная контрольная.
Приложения
Контрольные работы.
К.р. №1. 7 класс Вариант 1. I уровень
1. На луче с началом в точке А отмечены точки В и С. Найдите отрезок ВС, если
АВ= 9,2 см, АС= 2,4 см. Какая из точек лежит между двумя другими?
2. Один из углов, образовавшихся пр пересечении двух прямых, в четыре раза меньше другого. Найдите эти углы.
3. Луч с - биссектриса ![]() Луч d -биссектриса
Луч d -биссектриса ![]() Найдите
Найдите ![]() , если
, если ![]() .
.
4*. На рис. Дано: ![]() , ОК- биссектриса
, ОК- биссектриса ![]() Найти:
Найти: ![]()
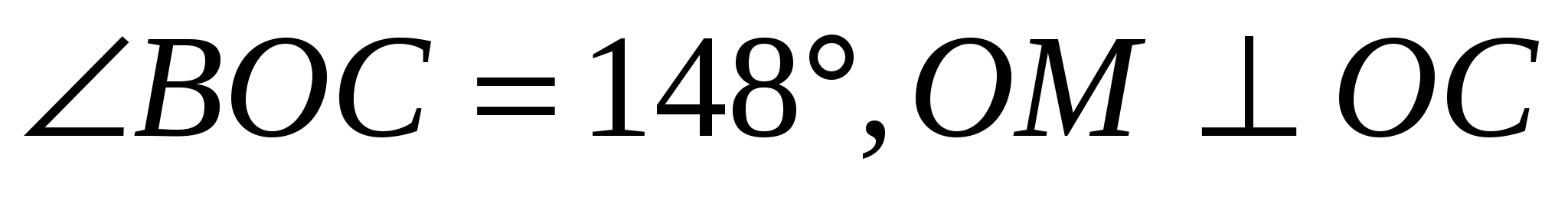
К.р. №1. 7 класс Вариант 2. I уровень
1. На луче с началом в точке А отмечены точки В и С. Найдите отрезок ВС, если
АВ= 3,8 см, АС= 5,6 см. Какая из точек лежит между двумя другими?
2. Один из углов, образовавшихся пр пересечении двух прямых, на 70º больше другого. Найдите эти углы.
3. Луч с - биссектриса ![]() Луч d -биссектриса
Луч d -биссектриса ![]() Найдите
Найдите ![]() , если
, если ![]() .
.
4*. На рис. Дано: ![]() , ОМ- биссектриса
, ОМ- биссектриса ![]() Найти:
Найти: ![]()
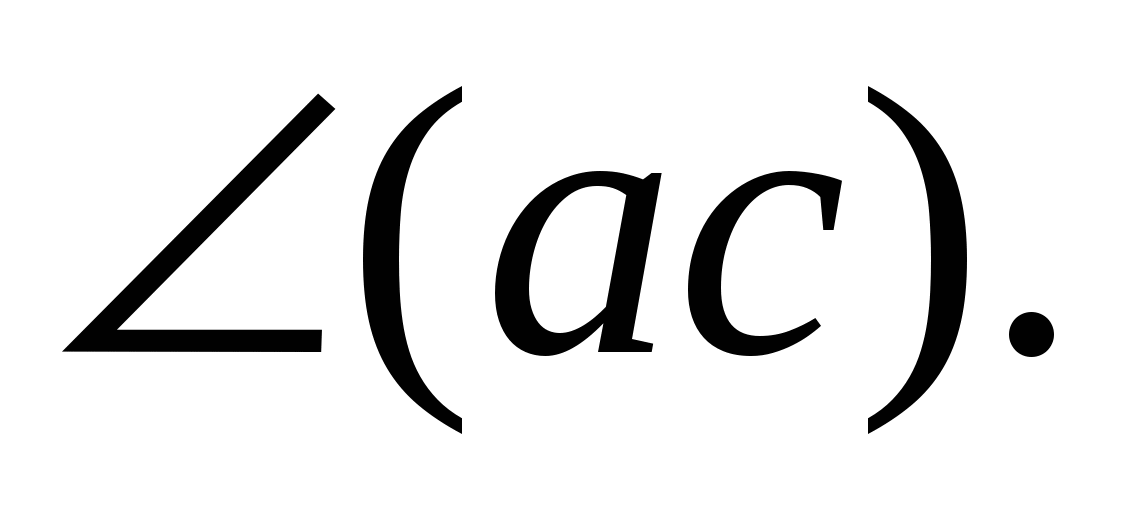
К.Р,№ 2 Геометрия (п. Атанасян Л.С.) Вариант 1. ( I уровень)
1. Дано: АО=ВО, СО=DO, CO= 5 см, BO=3 см, BD= 4 см. Найдите периметр ∆ САО.
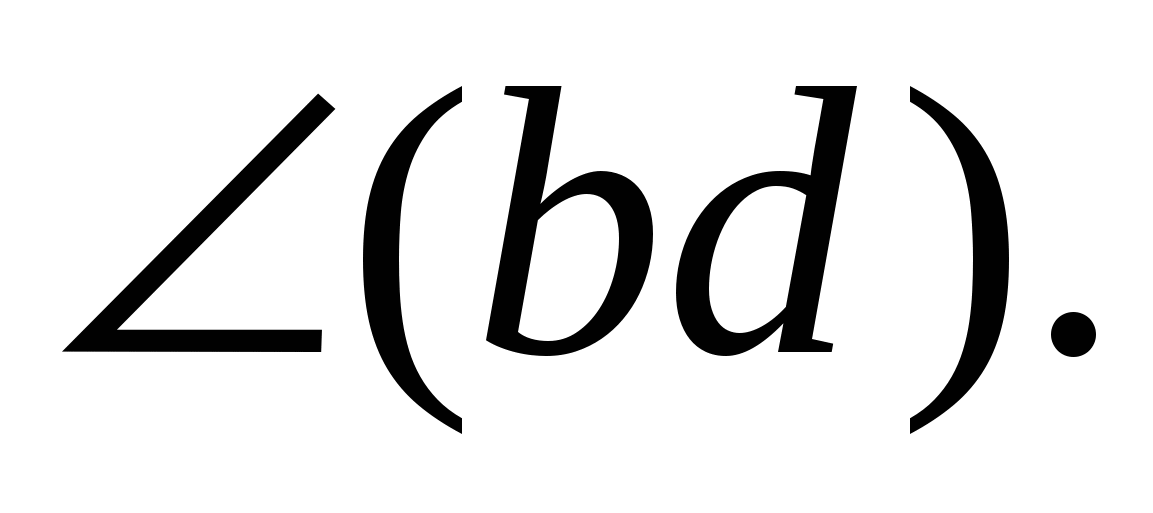 D
D
2.В равнобедренном треугольнике АВС точки К и М являются серединами боковых сторон АВ и ВС соответственно. ВD -медиана треугольника. Докажите, что ∆ВКD=∆ВМD.
3. Даны неразвернутый угол и отрезок. На сторонах угла постройте точки, удаленные от вершины угла на расстояние, равное половине данного отрезка.
4*. Прямая МК разбивает плоскость на две полуплоскости. Из точек М и К в разные полуплоскости проведены равные отрезки МА и КВ, причем ![]() Какие из высказываний верные?
Какие из высказываний верные?
А) ∆АМВ=∆АКВ б) ![]() АКМ=
АКМ=![]() ВМК в) ∆МКА=∆КМВ г)
ВМК в) ∆МКА=∆КМВ г) ![]() АМВ=
АМВ=![]() КМВ
КМВ
К.Р,№ 2 Геометрия (п. Атанасян Л.С.) Вариант 2. ( I уровень)
1. Дано: АВ=СD, BС=AD, AC= 7 см, AD=6 см, AB= 4 см. Найдите периметр ∆ АDC.
2.В равнобедренном треугольнике АВС точки К и М являются серединами боковых сторон АВ и ВС соответственно. ВD -медиана треугольника. Докажите, что ∆AКD=∆CМD.
3. Даны неразвернутый угол и отрезок. На биссектрисе данного угла постройте точку, удаленную от вершины угла на расстояние, равное данному отрезка.
4*. Прямая АВ разбивает плоскость на две полуплоскости. Из точек А и В в разные полуплоскости проведены равные отрезки АD и ВC, причем ![]() Какие из высказываний верные?
Какие из высказываний верные?
А) ∆CАD=∆ВDA б) ![]() в)
в) ![]() г)
г) ![]()
К.Р.№3. 1уровень Вариант 1. 7 класс Параллельные прямые.
1
a. Рис.1. Дано: а || b, c- секущая, ![]() 1 +
1 + ![]() 2 = 102º. Найти: все образованные углы.
2 = 102º. Найти: все образованные углы.
2. Рис.2. Дано: ![]() 1=
1=![]() 2,
2, ![]() 3=120º. Найти :
3=120º. Найти : ![]() 4.
4.
3.Отрезок АD - биссектриса треугольника АВС. Через точку D проведена прямая, параллельная стороне АВ и пересекающая сторону АС в точке F. Найти углы треугольника АDF, если ![]() ВАС = 72º.
ВАС = 72º.
4. Прямая ЕК является секущей для прямых СD и MN ( E ![]() CD, K
CD, K![]() MN).
MN). ![]() DEK равен 65º. При каком значении угла NKE прямые CD и MN могут быть параллельными?
DEK равен 65º. При каком значении угла NKE прямые CD и MN могут быть параллельными?
К.Р.№3. 1уровень Вариант 2. 7 класс Параллельные прямые.
1. Рис.1. Дано: а || b, c- секущая, ![]() 1 -
1 - ![]() 2 = 102º. Найти: все образованные углы.
2 = 102º. Найти: все образованные углы.
2. Рис.2. Дано: ![]() 1=
1=![]() 2,
2, ![]() 3=140º. Найти :
3=140º. Найти : ![]() 4.
4.
3.Отрезок АК - биссектриса треугольника САЕ. Через точку К проведена прямая, параллельная стороне СА и пересекающая сторону АЕ в точке N. Найти углы треугольника АКN, если ![]() САЕ = 78º.
САЕ = 78º.
4. Прямая MN является секущей для прямых АВ и СD ( М ![]() АВ, N
АВ, N![]() СD).
СD). ![]() АМN равен 75º. При каком значении угла СNМ прямые АВ и CD могут быть параллельными?
АМN равен 75º. При каком значении угла СNМ прямые АВ и CD могут быть параллельными?
К.Р. №4 Вариант 1. I уровень Геометрия 7 кл.
1. В ∆АВС АВ > BC > AC. Найдите ![]() А,
А, ![]() В,
В, ![]() С, если известно, что один из углов треугольника равен 120º, а другой 40º.
С, если известно, что один из углов треугольника равен 120º, а другой 40º.
2. В треугольнике АВС угол А равен 50º, а угол В в 12 раз меньше угла С. Найдите углы В и С.
3. В треугольнике АВС угол С равен 90º, а угол В равен 35º, СD- высота. Найдите углы треугольника АСD.
4. Периметр равнобедренного треугольника равен 45 см, одна из его сторон больше другой на 12 см. Найдите стороны треугольника.
К.Р. №4 Вариант 2. I уровень Геометрия 7 кл.
1. В ∆АВС АВ <BC <AC. Найдите ![]() А,
А, ![]() В,
В, ![]() С, если известно, что один из углов треугольника прямой, а другой 30º.
С, если известно, что один из углов треугольника прямой, а другой 30º.
2. В треугольнике АВС угол А равен 90º, а угол С на 40º больше угла В. Найдите углы В и С.
3. В треугольнике АВС угол С равен 90º, а угол А равен 70º, СD- биссектриса. Найдите углы треугольника ВСD.
4. Периметр равнобедренного треугольника равен 50 см, одна из его сторон на 13 см меньше другой . Найдите стороны треугольника.
К.Р.№5 7класс Вариант 1. Уровень 1.
1
В
С. На рис.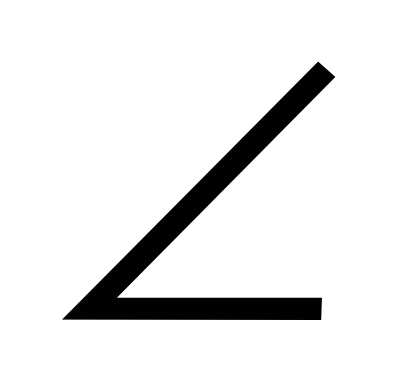
Дано: ![]() Доказать: AD ׀׀ BC.
Доказать: AD ׀׀ BC.
2. В треугольнике АВС ![]() Высота ВВ1 равна 2 см. Найдите АВ.
Высота ВВ1 равна 2 см. Найдите АВ.
3. Постройте равнобедренный треугольник по основанию и высоте, проведенной к нему из вершины треугольника.
4*. С помощью циркуля и линейки постройте угол, равный 150º.
К.Р.№5 7класс Вариант 2. Уровень 1.
1.На рис.
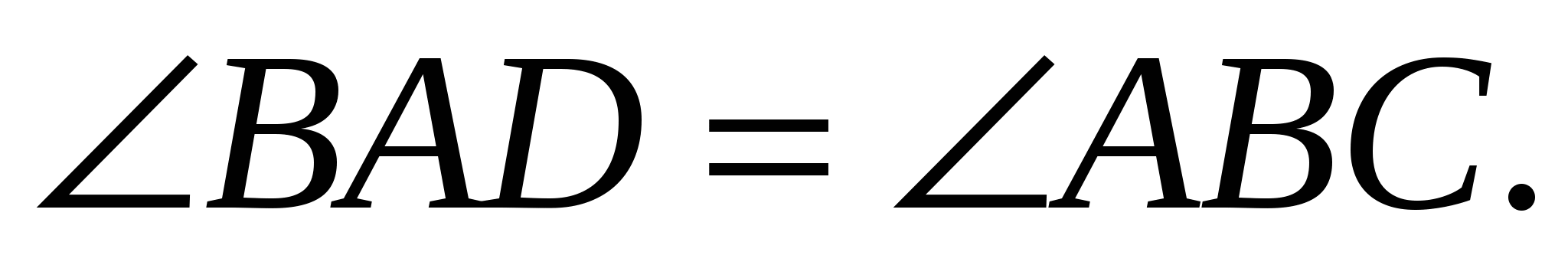
![]() Доказать: AD ׀׀ BC.
Доказать: AD ׀׀ BC.
2. В треугольнике АВС ![]() Высота СС1 равна 5 см, ВС= 10 см. Найдите
Высота СС1 равна 5 см, ВС= 10 см. Найдите ![]() .
.
3. Постройте равнобедренный треугольник по основанию и медиане, проведенной к нему из вершины треугольника.
4*. С помощью циркуля и линейки постройте угол, равный 120º.
К.Р.№5 7класс Вариант 1. Уровень 1.
1
В
С. На рис.
Дано: ![]() Доказать: AD ׀׀ BC.
Доказать: AD ׀׀ BC.
2. В треугольнике АВС ![]() Высота ВВ1 равна 2 см. Найдите АВ.
Высота ВВ1 равна 2 см. Найдите АВ.
3. Постройте равнобедренный треугольник по основанию и высоте, проведенной к нему из вершины треугольника.
4*. С помощью циркуля и линейки постройте угол, равный 150º.
25