Программа элективного курса по математике 8 класс

Муниципальное бюджетное общеобразовательное учреждение -

Приаргунская средняя общеобразовательная школа

«Рассмотрено»

Руководитель МО

____________Капишулина И.М

Протокол № ___ от

«____»____________20__ г.

«Согласовано»

Заместитель директора школы по УВР МБОУ Приаргунская СОШ

_____________ Лаптева М.М.

«____»____________20__ г.

«Утверждено»

Директор МБОУ Приаргунская СОШ

_____________Золотовская Г.И..

«___»_____________20__ г.

Батсуурь Солонго Аленксандровна

Программа элективного курса по математике

«Математика в вопросах и ответах»

для 8 «А» и «Б» классов

(математика - 1 час в неделю, 34 часа в год)

2016- 2017 учебный год

Экзаменационная работа за курс основной школы по математике состоит из двух частей. Часть 1 направлена на проверку достижений уровня базовой подготовки учащихся по математике. Часть 2 предназначена для дифференцированной проверки повышенного уровня математической подготовки учащихся.

Данный курс предназначен для дополнительной подготовки учащихся 8-го класса к итоговой аттестации по алгебре и включает в себя темы, необходимые для успешной сдачи второй части экзамена. Курс состоит из 4 разделов: «Числа и вычисления», «Выражения и преобразования», «Уравнения и неравенства», «Функции».

Цели и задачи:

• углубление и расширение знаний учащихся по изучаемым темам;

• подготовка учащихся к успешной сдачи экзамена за курс основной школы по новой форме.

Планируемые результаты освоения учебного предмета

Личностные результаты освоения учебного курса:

1. Российская гражданская идентичность. Осознанное, уважительное и доброжелательное отношение к истории, культуре, религии, традициям, языкам, ценностям народов России и народов мира.

2. Готовность и способность обучающихся к саморазвитию и самообразованию на основе мотивации к обучению и познанию; готовность и способность осознанному выбору и построению дальнейшей индивидуальной траектории образования на базе ориентировки в мире профессий и профессиональных предпочтений, с учетом устойчивых познавательных интересов.

3. Развитое моральное сознание и компетентность в решении моральных проблем на основе личностного выбора, формирование нравственных чувств и нравственного поведения, осознанного и ответственного отношения к собственным поступкам. Сформированность ответственного отношения к учению; уважительного отношения к труду, наличие опыта участия в социально значимом труде. Осознание значения семьи в жизни человека и общества, принятие ценности семейной жизни, уважительное и заботливое отношение к членам своей семьи.

4. Сформированность целостного мировоззрения, соответствующего современному уровню развития науки и общественной практики, учитывающего социальное, культурное, языковое, духовное многообразие современного мира.

5. Осознанное, уважительное и доброжелательное отношение к другому человеку, его мнению, мировоззрению, культуре, языку, вере, гражданской позиции. Готовность и способность вести диалог с другими людьми и достигать в нем взаимопонимания.

6. Освоенность социальных норм, правил поведения, ролей и форм социальной жизни в группах и сообществах. .

7. Сформированность ценности здорового и безопасного образа жизни; интериоризация правил индивидуального и коллективного безопасного поведения в чрезвычайных ситуациях, угрожающих жизни и здоровью людей, правил поведения на транспорте и на дорогах.

Метапредметные результаты освоения учебного курса:

Регулятивные УУД

1. Умение самостоятельно определять цели обучения, ставить и формулировать новые задачи в учебе и познавательной деятельности, развивать мотивы и интересы своей познавательной деятельности. Обучающийся сможет:

• анализировать существующие и планировать будущие образовательные результаты;

• идентифицировать собственные проблемы и определять главную проблему;

• выдвигать версии решения проблемы, формулировать гипотезы, предвосхищать конечный результат;

• ставить цель деятельности на основе определенной проблемы и существующих возможностей;

2. Умение самостоятельно планировать пути достижения целей, в том числе альтернативные, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач. Обучающийся сможет:

• определять необходимые действие(я) в соответствии с учебной и познавательной задачей и составлять алгоритм их выполнения;

• обосновывать выбор наиболее эффективных способов решения учебных и познавательных задач;

• определять/находить, в том числе из предложенных вариантов, условия для выполнения учебной и познавательной задачи;

• выбирать из предложенных вариантов средства/ресурсы для решения задачи/достижения цели;

• определять потенциальные затруднения при решении учебной и познавательной задачи и находить средства для их устранения;

3. Умение соотносить свои действия с планируемыми результатами, осуществлять контроль своей деятельности в процессе достижения результата, определять способы действий в рамках предложенных условий и требований, корректировать свои действия в соответствии с изменяющейся ситуацией. Обучающийся сможет:

• систематизировать (в том числе выбирать приоритетные) критерии планируемых результатов и оценки своей деятельности;

• отбирать инструменты для оценивания своей деятельности, осуществлять самоконтроль своей деятельности в рамках предложенных условий и требований;

• устанавливать связь между полученными характеристиками продукта и характеристиками процесса деятельности и по завершении деятельности предлагать изменение характеристик процесса для получения улучшенных характеристик продукта;

4. Умение оценивать правильность выполнения учебной задачи, собственные возможности ее решения. Обучающийся сможет:

• определять критерии правильности (корректности) выполнения учебной задачи;

• анализировать и обосновывать применение соответствующего инструментария для выполнения учебной задачи;

5. Владение основами самоконтроля, самооценки, принятия решений и осуществления осознанного выбора в учебной и познавательной. Обучающийся сможет:

• самостоятельно определять причины своего успеха или неуспеха;

Познавательные УУД

6. Умение определять понятия, создавать обобщения, устанавливать аналогии, классифицировать, самостоятельно выбирать основания и критерии для классификации, устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение (индуктивное, дедуктивное, по аналогии) и делать выводы. Обучающийся сможет:

• выстраивать логическую цепочку, состоящую из ключевого слова и соподчиненных ему слов;

• выделять общий признак двух или нескольких предметов или явлений и объяснять их сходство;

• объединять предметы и явления в группы по определенным признакам, сравнивать, классифицировать и обобщать факты и явления;

• делать вывод на основе критического анализа разных точек зрения.

7. Умение создавать, применять и преобразовывать знаки и символы, модели и схемы для решения учебных и познавательных задач. Обучающийся сможет:

• обозначать символом и знаком предмет и/или явление;

• определять логические связи между предметами и/или явлениями;

• строить модель/схему на основе условий задачи и/или способа ее решения;

• преобразовывать модели с целью выявления общих законов, определяющих данную предметную область;

8. Смысловое чтение. Обучающийся сможет:

• находить в тексте требуемую информацию (в соответствии с целями своей деятельности);

• ориентироваться в содержании текста, понимать целостный смысл текста.

Коммуникативные УУД

9. Умение организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками; работать индивидуально и в группе: находить общее решение и разрешать конфликты на основе согласования позиций и учета интересов; формулировать, аргументировать и отстаивать свое мнение. Обучающийся сможет:

• определять возможные роли в совместной деятельности;

• играть определенную роль в совместной деятельности;

• принимать позицию собеседника, понимая позицию другого, различать в его речи: мнение (точку зрения), доказательство (аргументы), факты; гипотезы, аксиомы, теории;

• строить позитивные отношения в процессе учебной и познавательной деятельности;

• корректно и аргументированно отстаивать свою точку зрения, в дискуссии уметь выдвигать контраргументы, перефразировать свою мысль (владение механизмом эквивалентных замен);

• критически относиться к собственному мнению, с достоинством признавать ошибочность своего мнения (если оно таково) и корректировать его;

• предлагать альтернативное решение в конфликтной ситуации.

10. Умение осознанно использовать речевые средства в соответствии с задачей коммуникации для выражения своих чувств, мыслей и потребностей для планирования и регуляции своей деятельности; владение устной и письменной речью, монологической контекстной речью. Обучающийся сможет:

• определять задачу коммуникации и в соответствии с ней отбирать речевые средства;

• высказывать и обосновывать мнение (суждение) и запрашивать мнение партнера в рамках диалога;

• принимать решение в ходе диалога и согласовывать его с собеседником;

• делать оценочный вывод о достижении цели коммуникации непосредственно после завершения коммуникативного контакта.

Предметные результаты освоения учебного курса:

Выпускник научится:

Элементы теории множеств и математической логики

• оперировать на базовом уровне понятиями: определение, аксиома, теорема, доказательство;

• приводить примеры и контрпримеры для подтверждения своих высказываний.

В повседневной жизни и при изучении других предметов:

• использовать графическое представление множеств для описания реальных процессов и явлений, при решении задач других учебных предметов.

Числа

• Оперировать на базовом уровне понятиями: рациональное число, арифметический квадратный корень;

• использовать свойства чисел и правила действий при выполнении вычислений;

• выполнять округление рациональных чисел в соответствии с правилами;

• оценивать значение квадратного корня из положительного целого числа;

• распознавать рациональные и иррациональные числа;

• сравнивать числа.

В повседневной жизни и при изучении других предметов:

• оценивать результаты вычислений при решении практических задач;

• выполнять сравнение чисел в реальных ситуациях;

• составлять числовые выражения при решении практических задач и задач из других учебных предметов.

Тождественные преобразования

• Выполнять несложные преобразования для вычисления значений числовых выражений, содержащих степени с натуральным показателем, степени с целым отрицательным показателем;

• выполнять несложные преобразования целых выражений: раскрывать скобки, приводить подобные слагаемые;

• выполнять несложные преобразования дробно-линейных выражений и выражений с квадратными корнями.

В повседневной жизни и при изучении других предметов:

• понимать смысл записи числа в стандартном виде;

• оперировать на базовом уровне понятием «стандартная запись числа».

Уравнения и неравенства

• проверять справедливость числовых равенств и неравенств;

• решать системы несложных линейных уравнений;

• проверять, является ли данное число решением уравнения;

• решать квадратные уравнения по формуле корней квадратного уравнения.

В повседневной жизни и при изучении других предметов:

• составлять и решать линейные уравнения при решении задач, возникающих в других учебных предметах.

Функции

• Находить значение функции по заданному значению аргумента;

• находить значение аргумента по заданному значению функции в несложных ситуациях;

• определять положение точки по её координатам, координаты точки по её положению на координатной плоскости;

• по графику находить область определения, множество значений, нули функции, промежутки знакопостоянства, промежутки возрастания и убывания, наибольшее и наименьшее значения функции;

• строить график линейной функции;

• проверять, является ли данный график графиком заданной функции (линейной, квадратичной, обратной пропорциональности);

• определять приближённые значения координат точки пересечения графиков функций.

В повседневной жизни и при изучении других предметов:

• использовать графики реальных процессов и зависимостей для определения их свойств (наибольшие и наименьшие значения, промежутки возрастания и убывания, области положительных и отрицательных значений и т.п.);

• использовать свойства линейной функции и ее график при решении задач из других учебных предметов.

Выпускник получит возможность научиться в 8 классе для обеспечения возможности успешного продолжения образования на базовом и углублённом уровнях

Элементы теории множеств и математической логики

• Оперировать¹ понятиями: определение, теорема, аксиома, множество, характеристики множества, элемент множества, пустое, конечное и бесконечное множество, подмножество, принадлежность, включение, равенство множеств;

• изображать множества и отношение множеств с помощью кругов Эйлера;

• определять принадлежность элемента множеству, объединению и пересечению множеств;

• строить высказывания, отрицания высказываний.

В повседневной жизни и при изучении других предметов:

• строить цепочки умозаключений на основе использования правил логики;

• использовать множества, операции с множествами, их графическое представление для описания реальных процессов и явлений.

Числа

• Оперировать понятиями: множество натуральных чисел, множество целых чисел, множество рациональных чисел, иррациональное число, квадратный корень, множество действительных чисел, геометрическая интерпретация натуральных, целых, рациональных, действительных чисел;

• понимать и объяснять смысл позиционной записи натурального числа;

• выполнять вычисления, в том числе с использованием приёмов рациональных вычислений;

• выполнять округление рациональных чисел с заданной точностью;

• сравнивать рациональные и иррациональные числа;

• представлять рациональное число в виде десятичной дроби.

В повседневной жизни и при изучении других предметов:

• применять правила приближенных вычислений при решении практических задач и решении задач других учебных предметов;

• выполнять сравнение результатов вычислений при решении практических задач, в том числе приближенных вычислений.

Тождественные преобразования

• Оперировать понятиями степени с натуральным показателем, степени с целым отрицательным показателем;

• выполнять преобразования целых выражений: действия с одночленами (сложение, вычитание, умножение), действия с многочленами (сложение, вычитание, умножение);

• выполнять разложение многочленов на множители одним из способов: вынесение за скобку, группировка, использование формул сокращенного умножения;

• выделять квадрат суммы и разности одночленов;

• раскладывать на множители квадратный трёхчлен;

• выполнять преобразования выражений, содержащих степени с целыми отрицательными показателями, переходить от записи в виде степени с целым отрицательным показателем к записи в виде дроби;

• выполнять преобразования дробно-рациональных выражений: сокращение дробей, приведение алгебраических дробей к общему знаменателю, сложение, умножение, деление алгебраических дробей, возведение алгебраической дроби в натуральную и целую отрицательную степень;

• выполнять преобразования выражений, содержащих квадратные корни;

• выделять квадрат суммы или разности двучлена в выражениях, содержащих квадратные корни.

В повседневной жизни и при изучении других предметов:

• выполнять преобразования и действия с числами, записанными в стандартном виде;

• выполнять преобразования алгебраических выражений при решении задач других учебных предметов.

Уравнения и неравенства

• Оперировать понятиями: уравнение, неравенство, корень уравнения, решение неравенства, равносильные уравнения, область определения уравнения;

• решать линейные уравнения и уравнения, сводимые к линейным с помощью тождественных преобразований;

• решать квадратные уравнения и уравнения, сводимые к квадратным с помощью тождественных преобразований;

• решать линейные уравнения с параметрами;

• решать несложные квадратные уравнения с параметром;

• решать несложные системы линейных уравнений с параметрами;

• решать несложные уравнения в целых числах.

В повседневной жизни и при изучении других предметов:

• составлять и решать линейные и квадратные уравнения, уравнения, к ним сводящиеся, системы линейных уравнений при решении задач других учебных предметов;

• уметь интерпретировать полученный при решении уравнения или системы результат в контексте заданной реальной ситуации или прикладной задачи.

Функции

• Оперировать понятиями: функциональная зависимость, функция, график функции, способы задания функции, аргумент и значение функции, область определения и множество значений функции, нули функции, промежутки знакопостоянства, монотонность функции, чётность/нечётность функции;

• на примере квадратичной функции, использовать преобразования графика функции y=f(x) для построения графиков функций ;

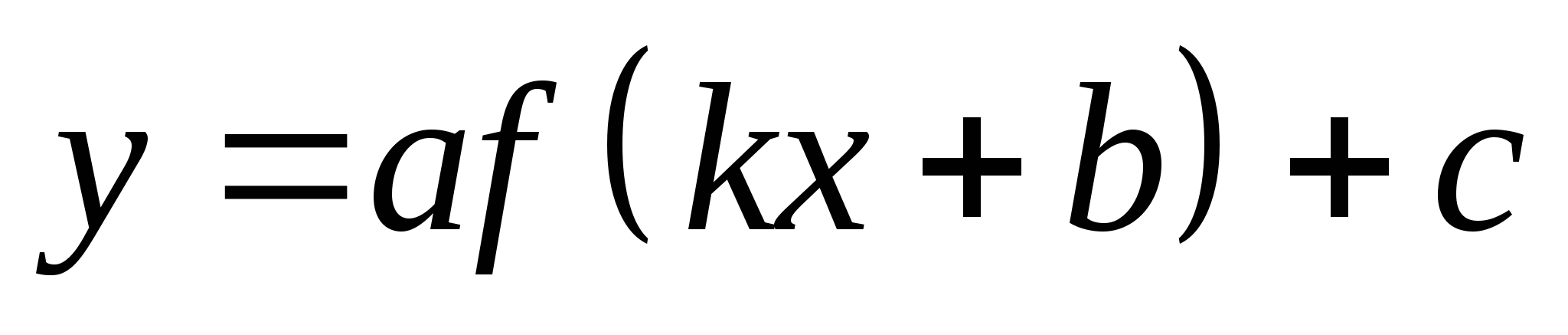• составлять уравнения прямой по заданным условиям: проходящей через две точки с заданными координатами, проходящей через данную точку и параллельной данной прямой;

• исследовать функцию по её графику;

• находить множество значений, нули, промежутки знакопостоянства, монотонности квадратичной функции.

В повседневной жизни и при изучении других предметов:

• иллюстрировать с помощью графика реальную зависимость или процесс по их характеристикам;

• использовать свойства и график квадратичной функции при решении задач из других учебных предметов.

Содержание курса

Числа и вычисления (11ч)

Рациональные числа. Стандартный вид числа. Проценты. Действия с рациональными числами. Сравнение рациональных чисел. Нахождение процента от числа. Нахождение числа по данной величине его процента. Нахождение процентного отношения двух чисел. Модуль числа. Степень с натуральным показателем. Квадратный корень. Свойства степени. Свойства квадратного корня.

Выражения и преобразования (11ч)

Буквенные выражения. Область определения буквенного выражения. Разложение на множители многочлена. Сложение, вычитание и умножение многочленов. Формулы сокращенного умножения. Алгебраическая дробь. Сокращение дробей. Действия с алгебраическими дробями. Преобразование рациональных выражений. Свойства квадратных корней и их применение в преобразования.

Уравнения и неравенства (7 ч)

Решение уравнения. Решение неравенства. Линейное уравнение. Линейное неравенство. Квадратное уравнение. Квадратное неравенство. Параметр. Уравнения с параметрами.

Функции (4 ч)

Линейная функция и ее свойства. Квадратичная функция и ее свойства.

Итоговая работа (1ч)

Календарно- тематическое планирование.

(1 час в неделю, 34 часа в год)

Числа и вычисления

11

1

Сравнение рациональных чисел

1

8.09

2

Действия с рациональными числами

1

15.09

3

Выполнение действий с числами, записанными в стандартном виде

1

22.09

4

Проценты

1

29.09

5

Основные задачи на проценты

1

6.10

6

Основные задачи на проценты

1

13.10

7

Противоположные числа. Модуль числа, геометрический смысл модуля.

1

20.10

8

Степень с натуральным показателем, вычисление значений выражений, содержащих степени

1

27.10

9

Степень с натуральным показателем, вычисление значений выражений, содержащих степени

1

10.11

10

Квадратный корень. Нахождение значений выражений, содержащих квадратный корень

1

17.11

11

Квадратный корень. Нахождение значений выражений, содержащих квадратный корень

1

24.11

Выражения и преобразования

11

12

Область определения буквенного выражения

1

1.12

13

Область определения буквенного выражения

1

8.12

14

Свойства степени с натуральным показателем, преобразование выражений, содержащих степени с натуральным показателем

1

15.12

15

Сложение, вычитание и умножение многочленов, формулы сокращенного умножения, преобразование целых выражений

1

22.12

16

Разложение многочленов на множители

1

12.01

17

Разложение многочленов на множители

1

19.01

18

Алгебраические дроби. Сокращение дробей. Действия с алгебраическими дробями

1

26.01

19

Рациональные выражения и их преобразования

1

2.02

20

Рациональные выражения и их преобразования

1

9.02

21

Свойства квадратных корней и их применение в преобразованиях

1

16.02

22

Свойства квадратных корней и их применение в преобразованиях

1

23.02

Уравнения и неравенства

7

23

Линейное уравнение

1

2.03

24

Линейное неравенство

1

9.03

25

Квадратное уравнение

1

16.03

26

Системы неравенств

1

23.03

27

Системы неравенств

1

6.04

28

Уравнения с параметрами

1

13.04

29

Уравнения с параметрами

1

20.04

Функции

4

30

Линейная функция и ее свойства

1

27.04

31

Линейная функция и ее свойства

1

4.05

32

Функция вида у= √х и ее свойства

1

11.05

33

Функции у=х² , у=х³ и их свойства

1

18.05

34

Итоговое занятие

1

25.05

И т о г о

34

1</<br>