Корень n-ой степени и его свойства.

Корень n-й степени и его свойства. 11 класс.

А.Г. Мордкович. Алгебра и начала анализа.

Цели урока:

• Образовательная: расширить и обобщить знания учащихся по данной теме, овладеть свойствами корня п-ой степени.

• Развивающая: развитие коммуникативных способностей.

• Воспитательная: формирование активной жизненной позиции, умение работать и преодолевать трудности, воспитание интереса к предмету.

Средства обучения: карточки, таблицы.

Тип урока: урок обобщения и систематизации знаний.

Форма обучения: индивидуальная и групповая.

Ход урока

«Мышление начинается с удивления»

Аристотель

1. Организационный момент: приветствие, выявление готовности учащихся к уроку, постановка цели.

2. Разминка.

3. Актуализация опорных знаний.

4. Обобщение и закрепление материала.

Ход урока.

Вопросы для разминки.

1. Так называют выражение хn. (степень)

2. Есть у любого слова, у растения, может быть n-й степени. (корень)

3. Степень корня, кратная 2. (четная)

4. Степень корня 2 k+1. (нечетная).

5. Как можно иначе назвать корень третьей степени? (кубический)

6. Действие, посредством которого отыскивают корень. (извлечение).

7. Положительный корень. (арифметический).

8. Как можно иначе назвать арифметический корень второй степени? (квадратный).

Актуализация опорных знаний.

а) Свойства арифметического квадратного корня:

= ∙ , а ≥ 0 , в ≥0

= , а≥0, b0

б) свойства степени с натуральным показателем:

=

Формирование новых знаний. Аналогично определению квадратного корня из числа a определяется корень n-ной степени из числа а, где n- произвольное натуральное число, n1.

Определение. Корнем n-ной степени из числа а называется такое число, n-ная степень которого равна а.

а)

б =2,

в) = -3

Рассмотрим уравнение = a. Число корней этого уравнения зависит от n и a.

Рассмотрим функцию f(x)=. При x и n -любое число- возрастает, и a имеет неотрицательный корень и только один x=.

Определение. Арифметическим корнем n-ной степени из числа a называют неотрицательное число, n -ая степень которого равна a.

При четном n существует два корня n-ной степени из любого положительного числа a, корень четной степени из отрицательных чисел не существует. При нечетном n существует корень n-ной из любого числа a и притом только один.

Краткая запись (в тетради).

n- четное число

=a, a>0

=

X= -

а) = 7 , 7 =343 в)= -3 = -243

основные свойства арифметических корней n-ной степени.

Для любых чисел n € N , k € N, n >1 и k>1 , a>0, b>0 выполняются равенства :

1. =∙ ;

2. = ;

3. = ;

4. 

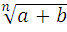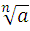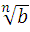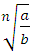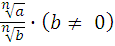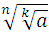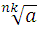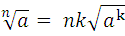
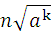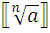5. =( ) k

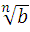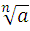6. > 0≤ a a>b

Обобщение и закрепление материала.

Задание 1. Вычислите.

а)

б)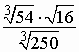

в)

Задание2. Докажите:

-=2

Задание3. Вычислите.

1) ∙ = = = 2

2) = = =

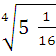3) = = -

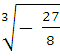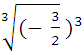Трехуровневая самостоятельная работа с целью проверить знания, умения и навыки по теме

« Корень п-ой степени и его свойства»

№ 1. Вычислить (А)

1вариант 2 вариант

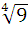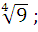1. ∙ 1) ;

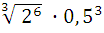2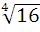. - 2 ; 2) ∙ ;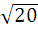

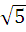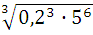3. ; 3) -6 ∙ ;

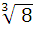№ 2 . Найдите значение выражения (В)

1) ∙ = 1) 7 ∙ =

2) = 2) =

№ 3. Упростите (С)

∙ ∙

Подведение итогов урока

Проверка работы учащихся: выставление оценок.