Учителю
Рабочая программа по математике 8 класс

Рабочая программа по математике 8 класс

Автор публикации: Поторочина С.С.

Дата публикации: 05.11.2014

Краткое описание: Рабочая программа по математике разработана на основании Закона РФ «Об образовании», в соответствии с требованиями Федерального компонента государственного стандарта общего образования и требования к оснащению образовательного процесса, примерной программы по ма

предварительный просмотр материала

Утверждаю

Директор

МАОУ СОШ № 17 города Тюмени

В.А. Кулик / /

Рассмотрено

Руководитель МО

МАОУ СОШ № 17 города Тюмени

_______________ / /

Протокол № …. от ……………..

Согласовано

Заместитель директора

МАОУ СОШ № 17 города Тюмени

_______________ / /

Рабочая программа

по учебному предмету «математика»

для обучающихся 8 класса

(базовый уровень)

МАОУ СОШ №17 города Тюмени

на 2014-2015 учебный год

Учитель математики Поторочина Светлана Степановна

Высшей квалификационной категории

Общее количество часов, отведенных на изучение алгебры - 102; количество часов в неделю - 3. Общее количество часов, отведенных на изучение геометрии - 68; количество часов в неделю - 2. Элективный курс «Решение текстовых задач» /дополнение и углубление/ - 34 часа /1 час в неделю/.

УМК:

Алгебра 8 класс (в двух частях: учебник, задачник) А.Г. Мордкович. Издательство «Мнемозина». 2012

Геометрия 7-9 классы. Учебник для общеобразовательных школ. Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Москва. Просвещение. 2010-2012

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

Рабочая программа по математике разработана на основании Закона РФ «Об образовании», в соответствии с требованиями Федерального компонента государственного стандарта общего образования и требования к оснащению образовательного процесса, примерной программы по математике общего образования, авторской программы А.Г. Мордковича, программы развития школы «Реализация информационно-технологического направления с дополнительной (углубленной) подготовкой по предметам математика и информатика и ИКТ», учебного плана и локальных актов МАОУ СОШ № 17 города Тюмени.

Цели обучения:

овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;

интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе, свойственных математической деятельности: ясности и точности мысли, критичности мышления, интуиции, логического мышления, элементов алгоритмической культуры, пространственных представлений, способности к преодолению трудностей;

формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;

формирование начальных представлений о сборе и группировке статистических данных, их наглядной интерпретации;

воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, играющей особую роль в общественном развитии.

Задачи обучения:

приобретения математических знаний и умений;

овладение обобщенными способами мыслительной, творческой, поисковой деятельностей;

Методы обучения:

методы организации и осуществления учебно-познавательной деятельности: словесный (диалог, рассказ и др.); наглядный (опорные схемы, слайды и др.); практический (упражнения, практические работы, решение задач, моделирование и др.); исследовательский; самостоятельной работы; работы под руководством преподавателя; дидактическая игра;

методы стимулирования и мотивации: интереса к учению; долга и ответственности в учении;

методы контроля и самоконтроля в обучении: фронтальная устная проверка, индивидуальный устный опрос, письменный контроль (контрольные и практические работы, тестирование, письменный зачет, тесты).

Формы текущего и итогового контроля: самостоятельная работа, тестирование, теоретические диктанты, контрольные работы.

Содержание курса (170 ч)

Алгебра (102 ч)

Алгебраические дроби. (21)

Основное свойство дроби, сокращение дробей. Сложение и вычитание алгебраических дробей. Умножение и деление алгебраических дробей. Возведение алгебраической дроби в степень. Преобразование рациональных выражений. Первые представления о решении рациональных уравнений. Степень с рациональным показателем.

Функция у=. Свойства квадратного корня. (18)

Рациональные числа. Понятие квадратного корня из неотрицательного числа. Иррациональные числа. Множество действительных чисел. Свойства числовых неравенств. Функция у=, её свойства и график. Свойства квадратных корней. Преобразование выражений, содержащих операцию извлечения квадратного корня. Алгоритм извлечения квадратного корня. Модуль действительного числа. График функции у=, формула

Квадратичная функция. Функция у=k/х. (18)

Функция у=kх², её свойства и график. Функция у=k/х, её свойства и график. Как построить график функции у=f (х+l)+m, если известен график функции у=f(х). Функция у=ах²+bх+с, её свойства и график. Графическое решение квадратных уравнений. Дробно-линейная функция, её свойства и график. Как построить графики функций у=│f(х)│и у=f│х│, если известен график функции у=f(х).

Квадратные уравнения. (23)

Основные понятия, связанные с квадратными уравнениями. Формулы корней квадратных уравнений. Теорема Виета. Разложение квадратного трёхчлена на линейные множители. Рациональные уравнения как математические модели реальных ситуаций.

Неравенства. (14) Многочлены от одной переменной. Уравнения высших степеней. Рациональные уравнения. Уравнения с модулями и параметрами. Иррациональные уравнения. Линейные неравенства. Квадратные неравенства. Доказательство неравенств. Приближённые вычисления. Стандартный вид положительного числа.

Повторение (8)

Геометрия (68 ч)

Четырёхугольники. (14)

Многоугольник, выпуклый и невыпуклый многоугольник, формула суммы углов выпуклого многоугольника, периметр многоугольника. Параллелограмм.

Свойства и признаки параллелограмма. Трапеция, виды трапеций, равнобедренная трапеция. Теорема Фалеса. Задачи на построение. Прямоугольник, свойства и признаки.

Ромб, квадрат; свойства и признаки. Осевая и центральная симметрии.

Площадь. (14)

Формулы для вычисления площадей многоугольников: прямоугольника, треугольника, трапеции. Теорема Пифагора. Теорема, обратная теореме Пифагора.

Подобные треугольники. (19)

Пропорциональные отрезки, сходственные стороны, подобные треугольники. Три признака подобия треугольников, их применение. Средняя линия треугольника. Свойство медиан треугольника. Пропорциональные отрезки в прямоугольном треугольнике. Практические приложения подобия треугольников. Синус, косинус и тангенс острого угла прямоугольного треугольника. Значения синуса, косинуса и тангенса для углов 30, 45 и 60.

Окружность. (17)

Случаи взаимного расположения прямой и окружности, определение касательной, свойство и признак касательной. Центральный угол, вписанный угол, градусная мера дуги окружности, отрезки пересекающихся хорд. Свойства биссектрисы угла и серединного перпендикуляра к отрезку. Теорема о пересечении высот треугольника. Вписанная и описанная окружности.

Повторение (4)

Требования к уровню математической подготовки в 8 классе

Результаты обучения соответствуют требованиям к уровню подготовки обучающихся и соответствуют ФГОС:

Результаты обучения

1. Общие учебные умения

1.1 Умения связанные с познавательной деятельностью

планировать и осуществлять алгоритмическую деятельность, выполнять заданные и конструировать новые алгоритмы;

решать разнообразные классы задач из различных разделов курса, в том числе задач, требующих поиска пути и способов решения;

уметь проводить исследовательскую деятельность, обобщать, ставить и формулировать новые задачи;

уметь ясно, точно, грамотно излагать свои мысли в устной и письменной речи, использовать различные языки математики (словесный, символический, графический), свободно переходить с одного языка на другой для иллюстрации, интерпретации, аргументации и доказательства;

проводить доказательные рассуждения, аргументацию, выдвигать гипотезы и их обоснование;

уметь проводить поиск, систематизацию, анализ и классификацию информации, использовать разнообразные информационные источники, включая учебную и справочную литературу, современные информационные технологии.

1.2 Умения, связанные с информационно-коммуникативной деятельностью

понимать существо математического доказательства; приводить примеры доказательств;

использовать математические формулы, уравнения; примеры их применения для решения математических и практических задач;

понимать, как потребности практики привели математическую науку к необходимости расширения понятия числа;

понимать вероятностный характер многих закономерностей окружающего мира; примеры статистических закономерностей и выводов;

знать каким образом геометрия возникла из практических задач землемерия; примеры геометрических объектов и утверждений о них, важных для практики;

понимать смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации.

2. Специальные предметные умения

Алгебра

Уметь

распознавать алгебраические дроби;

находить множество допустимых значений переменной алгебраической дроби;

дать оценку информации, фактам, процессам, определять их актуальность

применять основное свойство дроби при преобразовании алгебраических дробей и их сокращении;

находить значение дроби при заданном значении переменной

складывать и вычитать дроби с одинаковыми знаменателями;

находить общий знаменатель нескольких дробей;

самостоятельно складывать и вычитать дроби с одинаковыми и разными знаменателями;

применять основное свойство дроби при преобразовании алгебраических дробей и их сокращении;

находить значение дроби при заданном значении переменной

пользоваться алгоритмами умножения и деления дробей, возведения дроби в степень, упрощая выражения;

упрощать выражения, используя определение степени с отрицательным показателем и свойства степени;

решать рациональные уравнения способом освобождения от знаменателей, составляя математическую модель реальной ситуации

извлекать квадратные корни из неотрицательного числа;

решать задачи с целочисленными неизвестными;

строить график функции , знать её свойства;

применять свойства квадратных корней для упрощения выражений и вычисления корней;

выполнять преобразования, содержащие операцию извлечения корня, освобождаться от иррациональности в знаменателе;

применять свойства модуля;

строить график функции y = kx²; добывать информацию по заданной теме в источниках различного типа

строить график функции ;

строить график функции вида y = f(x + l) + m, описывать свойства функции по ее графику;

строить графики, заданные таблично и формулой;

описывать свойства по графику;

решать неполные квадратные уравнения и полные квадратные уравнения, разложив его левую часть на множители;

решать квадратные уравнения по формулам корней квадратного уравнения через дискриминант;

решать рациональные уравнения по заданному алгоритму и методом введения новой переменной;

решать задачи на числа, на движение по дороге, на движение по воде, выделяя основные этапы математического моделирования;

решать квадратные уравнения с четным вторым коэффициентом по алгоритму;

применять теорему Виета и обратную теорему Виета, решая квадратные уравнения;

решать иррациональные уравнения методом возведения в квадрат обеих частей уравнения, применяя свойства равносильных преобразований;

применять свойства числовых неравенств и неравенство Коши при доказательстве числовых неравенств;

решать неравенства с переменной и системы неравенств с переменной;

решать квадратные неравенства по алгоритму и методом интервалов;

построить и исследовать на монотонность функции: линейную, квадратную, обратной пропорциональности, функцию корень;

решать рациональные уравнения по заданному алгоритму и методом введения новой переменной;

решать квадратные уравнения с четным вторым коэффициентом по алгоритму;

применять теорему Виета и обратную теорему Виета, решая квадратные уравнения;

применять свойства числовых неравенств и неравенство Коши при доказательстве числовых неравенств;

решать неравенства с переменной и системы неравенств с переменной;

решать квадратные неравенства по алгоритму и методом интервалов;

Геометрия

Уметь

объяснить, какая фигура называется многоугольником, назвать его элементы;

вывести формулу суммы углов выпуклого многоугольника и решать задачи;

находить углы многоугольников, их периметры;

доказывать свойства и признак параллелограмма и применять при решении задач;

применять теорему Фалеса при решении задач

выполнять деление отрезка на n равных частей с помощью циркуля и линейки, используя свойства параллелограмма и равнобедренной трапеции;

выполнять задачи на построение четырехугольников;

доказывать изученные теоремы и применять их при решении задач;

строить симметричные точки и распознавать фигуры, обладающие осевой симметрией и центральной симметрией;

вывести формулу для вычисления площади прямоугольника и использовать ее при решении задач;

применять теоремы при решении задач;

определять подобные треугольники, находить неизвестные величины из пропорциональных отношений, применять теорию при решении задач;

находить неизвестную величину в прямоугольном треугольнике;

доказывать признаки подобия и применять их при решении задач

с помощью циркуля и линейки делить отрезок в данном отношении и решать задачи на построение;

применять все изученные формулы, значения синуса, косинуса, тангенса, метрические соотношения при решении задач;

выполнять задачи на построение окружностей и касательных, определять отрезки хорд окружностей;

выполнять построение замечательных точек треугольника;

применять все изученные теоремы при решении задач;

Знать

какая окружность называется вписанной в многоугольник и какая, описанной около многоугольника;

теоремы об окружности, вписанной в треугольник, и об окружности, описанной около треугольника;

свойства вписанного и описанного четырехугольников;

основные свойства площадей и формулу для вычисления площади прямоугольника;

формулы для вычисления площадей параллелограмма, треугольника и трапеции;

теорему об отношении площадей треугольников, имеющих по равному углу;

теорему Пифагора и обратную ей теорему, область применения, пифагоровы тройки;

определения пропорциональных отрезков и подобных треугольников, теорему об отношении подобных треугольников и свойство биссектрисы треугольника;

признаки подобия треугольников, определение пропорциональных отрезков;

теоремы о средней линии треугольника, точке пересечения медиан треугольника и пропорциональных отрезках в прямоугольном треугольнике;

определения синуса, косинуса и тангенса острого угла прямоугольного треугольника, значения синуса, косинуса и тангенса для углов 30, 45 и 60, метрические соотношения;

признаки подобия треугольников, определение пропорциональных отрезков;

возможные случаи взаимного расположения прямой и окружности, определение касательной, свойство и признак касательной;

Критерии и нормы оценки знаний, умений и навыков обучающихся по математике

Оценка письменных контрольных работ обучающихся по математике.

Ответ оценивается отметкой «5», если:

работа выполнена полностью;

в логических рассуждениях и обосновании решения нет пробелов и ошибок;

в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).

Отметка «4» ставится в следующих случаях:

работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);

допущены одна ошибка или есть два - три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).

Отметка «3» ставится, если:

допущено более одной ошибки или более двух - трех недочетов в выкладках, чертежах или графиках, но обучающийся обладает обязательными умениями по проверяемой теме.

Отметка «2» ставится, если:

допущены существенные ошибки, показавшие, что обучающийся не обладает обязательными умениями по данной теме в полной мере.

Отметка «1» ставится, если:

работа показала полное отсутствие у обучающегося обязательных знаний и умений по проверяемой теме или значительная часть работы выполнена не самостоятельно.

Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии обучающегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные обучающемуся дополнительно после выполнения им каких-либо других заданий.

Оценка устных ответов обучающихся по математике.

Ответ оценивается отметкой «5», если ученик:

полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;

изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;

правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;

показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;

продемонстрировал знание теории ранее изученных сопутствующих тем, сформированность и устойчивость используемых при ответе умений и навыков;

отвечал самостоятельно, без наводящих вопросов учителя;

возможны одна - две неточности при освещение второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя.

Ответ оценивается отметкой «4», если удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:

в изложении допущены небольшие пробелы, не исказившее математическое содержание ответа;

допущены один - два недочета при освещении основного содержания ответа, исправленные после замечания учителя;

допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.

Отметка «3» ставится в следующих случаях:

неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для усвоения программного материала (определены «Требованиями к математической подготовке обучающихся» в настоящей программе по математике);

имелись затруднения или допущены ошибки в определении математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;

ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;

при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.

Отметка «2» ставится в следующих случаях:

не раскрыто основное содержание учебного материала;

обнаружено незнание учеником большей или наиболее важной части учебного материала;

допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.

Отметка «1» ставится, если:

ученик обнаружил полное незнание и непонимание изучаемого учебного материала или не смог ответить ни на один из поставленных вопросов по изученному материалу.

Общая классификация ошибок.

При оценке знаний, умений и навыков обучающихся следует учитывать все ошибки (грубые и негрубые) и недочёты.

3.1. Грубыми считаются ошибки:

незнание определения основных понятий, законов, правил, основных положений теории, незнание формул, общепринятых символов обозначений величин, единиц их измерения;

незнание наименований единиц измерения;

неумение выделить в ответе главное;

неумение применять знания, алгоритмы для решения задач;

неумение делать выводы и обобщения;

неумение читать и строить графики;

неумение пользоваться первоисточниками, учебником и справочниками;

потеря корня или сохранение постороннего корня;

отбрасывание без объяснений одного из них;

равнозначные им ошибки;

вычислительные ошибки, если они не являются опиской;

логические ошибки.

3.2. К негрубым ошибкам следует отнести:

неточность формулировок, определений, понятий, теорий, вызванная неполнотой охвата основных признаков определяемого понятия или заменой одного - двух из этих признаков второстепенными;

неточность графика;

нерациональный метод решения задачи или недостаточно продуманный план ответа (нарушение логики, подмена отдельных основных вопросов второстепенными);

нерациональные методы работы со справочной и другой литературой;

неумение решать задачи, выполнять задания в общем виде.

3.3. Недочетами являются:

нерациональные приемы вычислений и преобразований;

небрежное выполнение записей, чертежей, схем, графиков.

Основная литература:

А.Г. Мордкович Алгебра 8 класс. Учебник для общеобразовательных учреждений - М.: Мнемозина, 2010-2012;

А.Г. Мордкович, Т.Н. Мишустина, Е.Е. Тульчинская. Алгебра 8 класс. Задачник для общеобразовательных учреждений - М.: Мнемозина, 2010-2012;

А.Г. Мордкович, Е.Е Тульчинская Алгебра: Тесты для 7 - 9 классов общеобразовательных учреждений. - М.: Мнемозина, 2007;

Ю.П. Дудницын, Е.Е. Тульчинская Алгебра. 8 класс. Контрольные работы для общеобразовательных учреждений. - М.: Мнемозина, 2007.

А.Г. Мордкович. Алгебра. Методическое пособие для учителя. М., Мнемозина, 2007

Л.С. Атанасян и др. Геометрия, 7-9. Учебник. М.: Просвещение, 2010-2012

Учебно-методический комплекс учителя:

1. Изучение геометрии в 7-9 классах: пособие для учителей./ Л.С. Атанасян, В.Ф. Бутузов, Ю.А. Глазков и др.- М.: Просвещение, 2009. - 255 с.

2. Жохов В.И., Карташева Г.Д., Крайнева Л.Б. Уроки геометрии в 7-9 классах: Методические рекомендации для учителя к учебнику Атанасяна Л.С. и др. - М.: Вербум-М, 2003

3. Геометрия. 8 класс: поурочные планы по учебнику Атанасяна Л.С. и др./ авт.-сост. Т.Л.Афанасьева, Л.А.Тапилина. - 4-е изд., испр. - Волгоград: Учитель, 2010

4. Мищенко Т.М. Геометрия. Тематические тесты. 8 класс / Т.М.Мищенко, А.Д.Блинков. - М.: Просвещение, 2008

5. Тематические тесты по геометрии: к учебнику Л.С. Атанасян и др., 8 кл. / Т.М. Мищенко. - М.: Издательство «Экзамен», 2007. - 61 с.

6. Геометрия. Тесты. 7 - 9 кл.: Учебно-метод. пособие./ П.И. Алтынов. - М.: Дрофа, 1999. - 112 с.

7. Дидактические материалы по геометрии. 8 класс. / Б.Г. Зив, В.М. Мейлер. / М: Просвещение, 2008г - 126 с.

8. Задачи и упражнения на готовых чертежах. 7-9 классы. Геометрия./ Е.М. Рабинович. - М.: Илекса, Харьков: Гимназия, 2001. - 56 с.

9. Геометрия. 8 класс. Рабочая тетрадь: В 2 ч. / А.В. Рогулева. - Саратов: Лицей, 2006. - Ч.1. - 80 с. (Ч.2. - 80 с.)

10. Фарков А.В. Математические кружки в школе.5-8 класс - М.: Айрис-пресс, 2006.

Дополнительная литература для учащихся:

Энциклопедия. Я познаю мир. Математика. - М.: ООО «Издательство АСТ», 2004.

Черкасов О.Ю. Математика. Справочник / О.Ю. Черкасов, А.Г. Якушев. - М.: АСТ-ПРЕСС ШКОЛА, 2006.

Интернет-ресурс

1. www. - "Российское образование" Федеральный портал.

2. www. - "Российский общеобразовательный портал".

3. www.school-collection.edu.ru/ Единая коллекция цифровых образовательных ресурсов

4. www.mathvaz.ru -
5.

6. www . Фестиваль педагогических идей "Открытый урок"

7. www.shomtaya.ucoz.ru/ Персональный сайт - Шомахова Таисия Исмаиловна.

8. - единая коллекция цифровых образовательных ресурсов.

9. - Уроки по основным предметам школьной программы.

10. http://сдамгиа.рф/ - сдам ГИА

Письменный контролирующий материал

Алгебра 8

Контрольная работа № 1

Вариант 1

1^о. При каких значениях переменной алгебраическая дробь не имеет смысла?

2^о. Найти значение выражения

при х = -1,5

3^о. Выполните действия

а) б) в) г)

4^о. Прогулочный теплоход по течению реки проплывает 12км за такое же время, что и 10км против течения. Найдите скорость течения реки, если собственная скорость теплохода 22км/ч.

5. Докажите, что при всех допустимых значениях переменной значение выражения положительно.

Контрольная работа № 1

Вариант 2

1^о. При каких значениях переменной алгебраическая дробь не имеет смысла?

2^о. Найти значение выражения

при х = -

3^о. Выполните действия

а) б) в) г)

4^о. Туристы проплыли на лодке по озеру 18км за такое же время, что и 15км против течения реки. Найдите скорость лодки по озеру, если скорость течения реки 2 км/ч.

Докажите, что при всех допустимых значениях переменной значение выражения отрицательно.

Кодификатор

№ умения

Проверяемое умение

№ задания

Уметь определять смысл алгебраических дробей

Уметь прибавлять а.д. с одинаковым знаменателем.

Уметь прибавлять а.д. с разными знаменателями.

Уметь решать задачи на движение по реке

Уметь доказывать тождество с применением ФСУ

Контрольная работа № 2

Вариант 1

1^о. Выполните действия: а) б)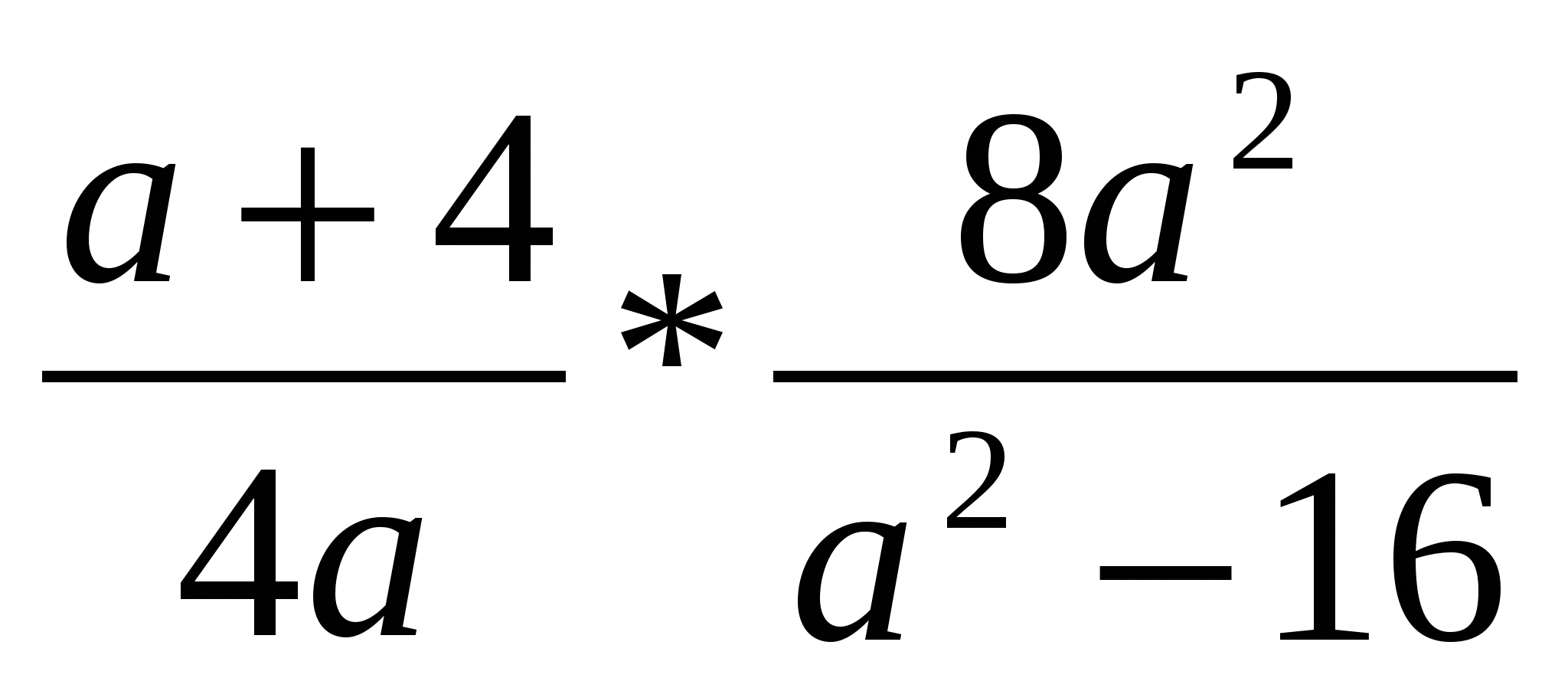

2^о. Вычислите:

3^о. Решить уравнение х + 81х^-1 = 18

4^о. Упростить выражение:

Из пункта М в пункт N, расстояние между которыми 4,5км, вышел пешеход. Через 45мин. вслед за ним выехал велосипедист, скорость которого в 3 раза больше скорости пешехода. Найти скорость пешехода, если в пункт N они прибыли одновременно.

Контрольная работа № 2

Вариант 2

1^о. Выполните действия: а) б)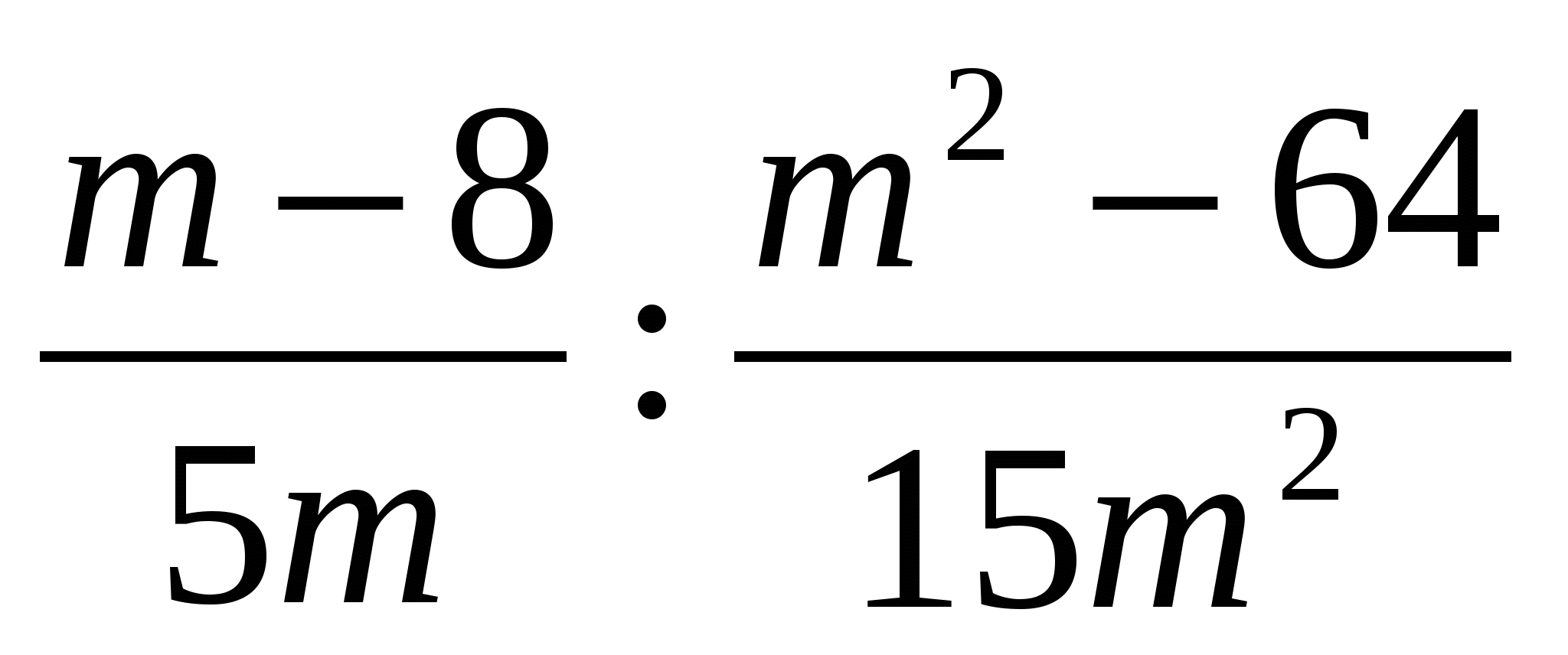

2^о. Вычислите:

3^о. Решить уравнение х - 100х^-1 = 0

4^о. Упростить выражение:

5. Из города А в город В, расстояние между которыми 200км, выехал автобус. Через 1 ч 20мин вслед за ним выехал автомобиль, скорость которого в 1,5 раза больше скорости автобуса. Найти скорость автобуса, если в город В они прибыли одновременно.

Кодификатор

№ умения

Проверяемое умение

№ задания

Уметь умножать и делить алгебраические дроби

Уметь сокращать числовые выражения с отрицательной степенью

Уметь решать уравнения с отрицательной степенью

Уметь упрощать рациональные выражения

Уметь решать задачи на движение.

Контрольная работа № 3

Вариант 1

1^о. Вычислите: а) б)

2^о. Постройте график функции у = . С помощью графика найдите:

а) наибольшее и наименьшее значения функции на отрезке [4;7]

б) координаты точки пересечения графика данной функции с прямой х - 2у = 0

3^о. Сократите дробь:

4.Сравните значения выражений А и В, если А =

5.Докажите равенство:

Контрольная работа № 3

Вариант 2

1^о. Вычислите: а) б)

2^о. Постройте график функции у = - . С помощью графика найдите:

а) наибольшее и наименьшее значения функции на отрезке [5;9]

б) координаты точки пересечения графика данной функции с прямой х + 3у = 0

3^о. Сократите дробь:

4.Сравните значения выражений А и В, если А = 0,(15), В =

5.Докажите равенство:

Кодификатор

№ умения

Проверяемое умение

№ задания

Уметь вычислять выражения с корнями

Уметь строить и исследовать функцию у = - .

Уметь сокращать дроби, содержащие корни

Уметь сравнивать дроби с выражением, содержащим корень

Уметь доказывать тождества, содержащие корни

Контрольная работа № 4

Вариант 1

1^о. Постройте график функции у = 0,5х². С помощью графика найдите:

а) значение функции при значении аргумента, равном -2; 3; 4;

б) значение аргумента, если значение функции равно 2;

в) значение аргумента, при которых у < 2;

г) наибольшее и наименьшее значения функции на отрезке [-1;2]

2^о. Решите графически уравнение:

3^о. Задайте формулой гиперболу , если известно, что она проходит через точку А(-3;4). Принадлежит ли графику заданной функции точка В(2; -2)

4. Даны функции у = f(x) и у = g(x), где f(x) = х² , g(x) = 3x². При каких значениях аргумента выполняется равенство f(2x + 3) = g(x + 2)

5. Найти корни уравнения

Контрольная работа № 4

Вариант 2

1^о. Постройте график функции . С помощью графика найдите:

а) значение функции при значении аргумента, равном -10; -2; 5;

б) значение аргумента, если значение функции равно -5;

в) значение аргумента, при которых у > 1;

г) наибольшее и наименьшее значения функции на отрезке [-5;-1]

2^о. Решите графически уравнение:

3^о. Задайте формулой гиперболу , если известно, что она проходит через точку C(8;-3). Принадлежит ли графику заданной функции точка D(-; 4)

4. Даны функции у = f(x) и у = g(x), где f(x) =4 х² , g(x) = x². При каких значениях аргумента выполняется равенство f(x - 3) = g(x + 6)

5. Найти корни уравнения

Кодификатор

№ умения

Проверяемое умение

№ задания

Уметь строить и исследовать график квадратичной функции и обратной пропорциональности

Уметь решать уравнения графическим способом

Уметь восстановить функцию о.п. по данным точкам

Уметь составлять и решать уравнение

Уметь решать иррациональное уравнение

Контрольная работа № 5

Вариант 1

1^о. Постройте график функции а) б) Укажите область определения функции.

2^о. Постройте график функции у = х² - 2х - 3

С помощью графика найдите:

а) промежутки возрастания и убывания функции;

б) наименьшее значение функции;

в) при каких значениях х * у < 0

3^о. Решите графически квадратное уравнение -х² + 2х + 8 = 0

4^о. Решите графически систему уравнений

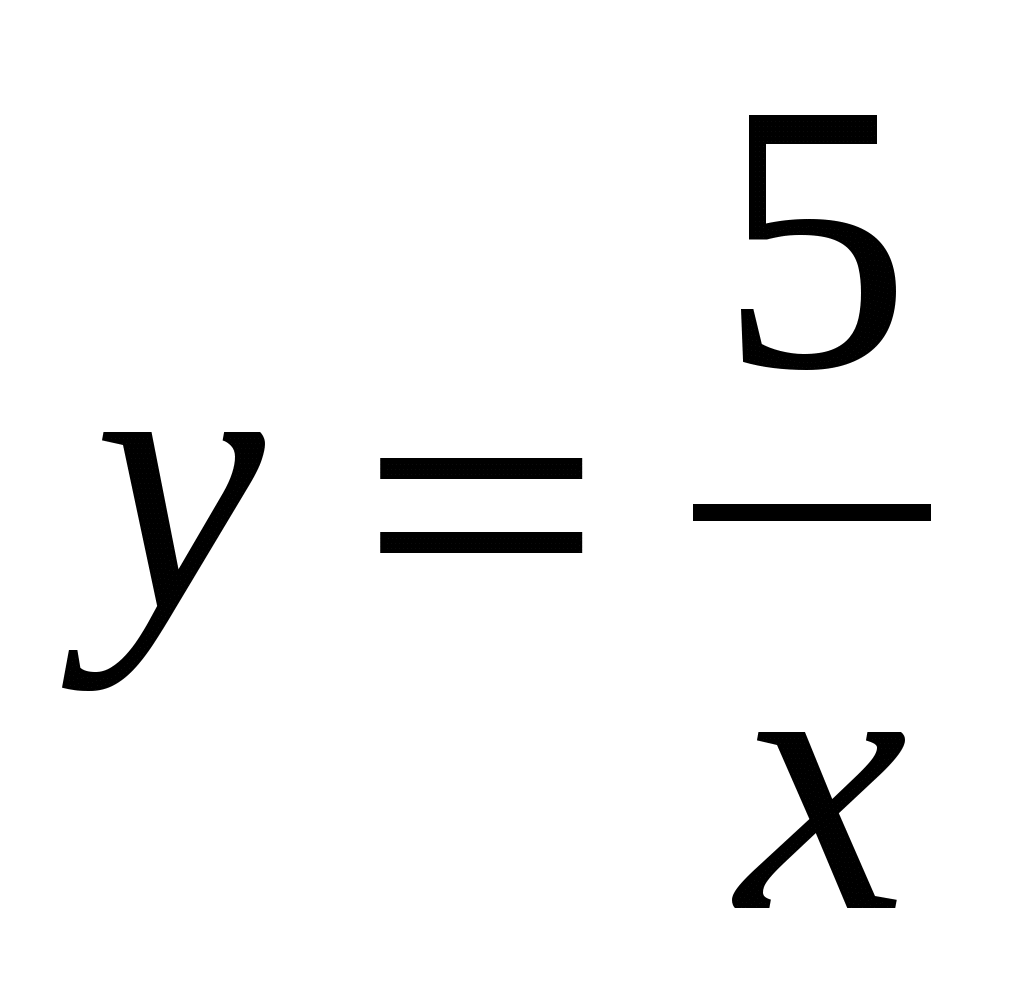у = - + 2

у = |x - 3| - 1

5. Найти значение параметра р и написать уравнение оси симметрии параболы, заданной формулой у = х² + рх - 24, если известно, что точка с координатами (4; 0) принадлежит графику данной функции.

Контрольная работа № 5

Вариант 2

1^о. Постройте график функции а) б) Укажите множество значений функции.

2^о. Постройте график функции у = -х² + 2х + 3

С помощью графика найдите:

а) промежутки возрастания и убывания функции;

б) наибольшее значение функции;

в) при каких значениях х * у < 0

3^о. Решите графически квадратное уравнение х² - 4х - 5 = 0

4^о. Решите графически систему уравнений

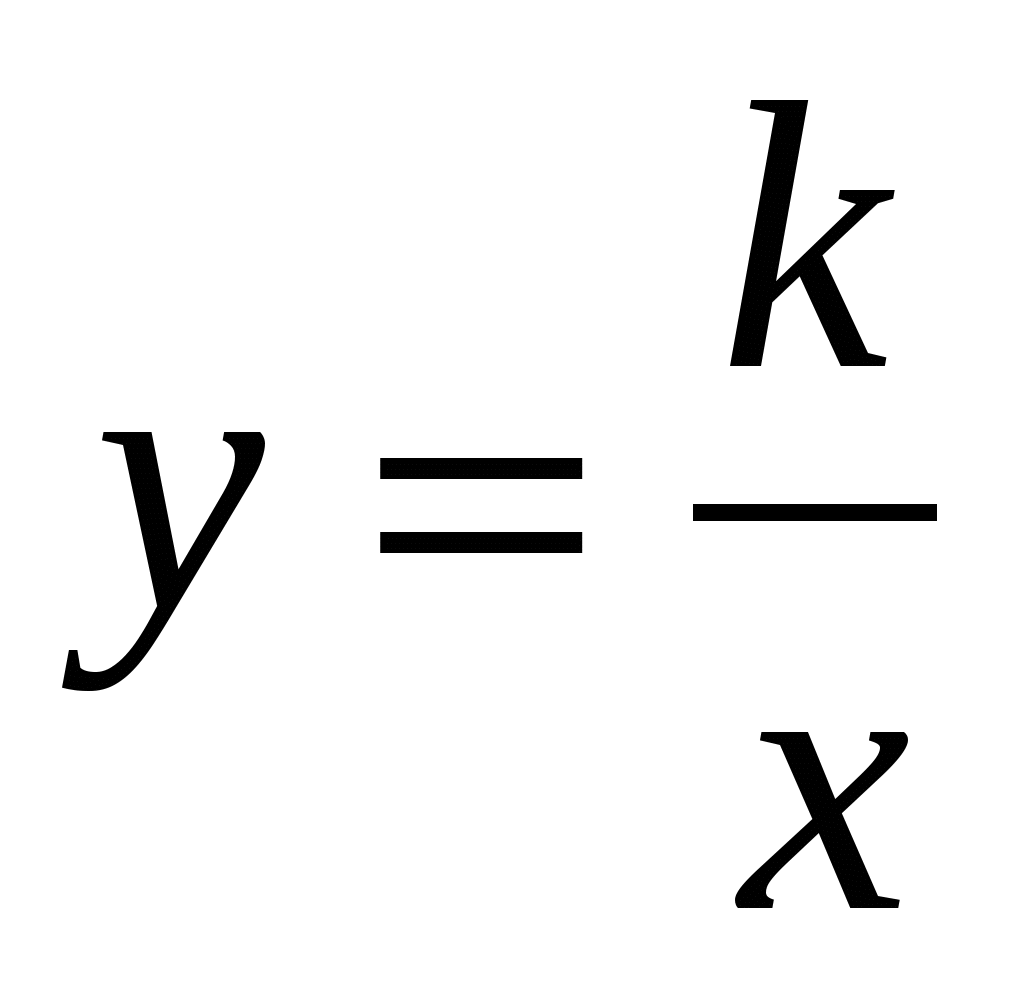у = + 4

у = |x - 3|

5. Найти значение параметра р и написать уравнение оси симметрии параболы, заданной формулой у = х² + рх + 35, если известно, что точка с координатами (5; 0) принадлежит графику данной функции.

Кодификатор

№ умения

Проверяемое умение

№ задания

Уметь строить и исследовать функцию с корнем

Уметь строить и исследовать квадратичную функцию

Уметь графически решать квадратное уравнение

Уметь графически решать систему уравнений

Уметь решать квадратное уравнение с параметром

Контрольная работа № 6

Вариант 1

1^о. Определите число корней квадратного уравнения

а) 9х² +12х + 4 = 0 б) 2х² + 3х - 11 = 0

2^о. Решите уравнение

а) х² - 14х + 33 = 0 б) -3х² + 10х - 3 = 0 в) х⁴ - 10х² + 9 = 0

3^о. Одна сторона прямоугольника на 9см больше другой. Найдите стороны прямоугольника, если его площадь равна 112см²

4. Решите уравнение

5. При каком значении р уравнение 4х² + рх + 9 = 0 имеет один корень

Контрольная работа № 6

Вариант 2

1^о. Определите число корней квадратного уравнения

а) 3х² + 7х - 25 = 0 б) 2х² + х + 5 = 0

2^о. Решите уравнение

а) х² - 11х - 42 = 0 б) -2х² - 5х - 2 = 0 в) х⁴ - 13х² + 36 = 0

3^о. Один катет прямоугольного треугольника на 5см меньше другого. Найдите длину каждого катета, если площадь треугольника равна 42см²

4. Решите уравнение

5. При каком значении р уравнение х² - рх + р = 0 имеет один корень

Кодификатор

№ умения

Проверяемое умение

№ задания

Уметь находить число корней квадратного уравнения

Уметь решать квадратные уравнения через дискриминант

Уметь решать задачи применяя квадратное уравнение

Уметь решать дробно-рациональные уравнения

Уметь решать квадратное уравнение с параметром.

Контрольная работа № 7

Вариант 1

1^о. Сократите дробь

2^о. Решите уравнение:

а) х² - 110х + 216 = 0 б) х² + 10х + 22 = 0

3^о. Упростите выражение

4. Один из корней квадратного уравнения х² - х + q = 0 на 4 больше другого. Найдите корни уравнения и значение q.

5. Из пункта А в пункт В, расстояние между которыми 240км, одновременно выехали два автомобиля: «ГАЗ - 53» и «Газель». Так как скорость «Газели» на 20км/ч больше скорости «ГАЗ - 53», то «Газель» прибыла в пункт В на 1ч раньше. Найдите скорость каждого автомобиля.

Контрольная работа № 7

Вариант 2

1^о. Сократите дробь

2^о. Решите уравнение:

а) х² + 106х + 693 = 0 б) х² + 6х + 4 = 0

3^о. Упростите выражение

4. Один из корней квадратного уравнения х² + 2х + q = 0 в 6 раз больше другого. Найдите корни уравнения и значение q.

5. Автомобиль проехал 60км по автостраде и 32км по шоссе, затратив на весь путь 1ч. найдите скорость автомобиля на каждом участке пути, если по автостраде он двигался на 20км/ч быстрее, чем по шоссе.

Кодификатор

№ умения

Проверяемое умение

№ задания

Уметь сокращать дроби, используя ФСУ

Уметь решать квадратные уравнения

Уметь упрощать дробно-рациональные выражения

Уметь решать квадратное уравнение с параметром, используя теорему Виета

Уметь решать задачи на движение.

Контрольная работа № 8

Вариант 1

Решите неравенство:

а) 9х - 11 > 5(2х - 3); б) х² + 7х - 8  0.

2. Решить уравнение:

а) 3х - 2 - 8 = 0 б)

3. Найти область определения выражения

4. Докажите, что функция возрастает.

5. При каких значениях параметра m уравнение mх² - 2mх + 9 = 0 имеет два корня?

Контрольная работа № 8

Вариант 2

1. Решите неравенство:

а) 22х + 5  3(6х - 1); б) х² - 11х + 24 < 0.

2. Решить уравнение:

а) 5х - 18 - 8 = 0 б)

3. Найти область определения выражения

4. Докажите, что функция убывает.

5. При каких значениях параметра m уравнение х² + 2mх - 7m = 0 не имеет корней ?

Кодификатор

№ умения

Проверяемое умение

№ задания

Уметь решать линейные и квадратные неравенства

Уметь решать иррациональные уравнения

Уметь находить о.о. выражения с корнем

Уметь доказывать монотонность функции

Уметь решать квадратные уравнения с параметром

Итоговая контрольная работа

Вариант 1

1. Постройте график функции у = -х² + 6х - 8.

Найдите:

а) наибольшее и наименьшее значения функции на отрезке [2; 5];

б) промежутки возрастания и убывания функции

в) решения неравенства -х² + 6х - 8 < 0

2. Решите уравнение 10х² - х - 60 = 0

3. Решите неравенство и найдите его наибольшее целочисленное решение.

4. Совместное предприятие по изготовлению вычислительной техники должно было изготовить 180 компьютеров. Изготавливая в день на 3 компьютера больше, предприятие выполнило задание на 3 дня раньше срока. Сколько компьютеров изготавливало предприятие в один день?

5. Дана функция у = f (x) , где f (x) =. Найдите f (x + 6), если

Итоговая контрольная работа

Вариант 2

1. Постройте график функции у = х² - 6х + 5.

Найдите:

а) наибольшее и наименьшее значения функции на отрезке [1; 4];

б) промежутки возрастания и убывания функции

в) решения неравенства х² - 6х + 5> 0

2. Решите уравнение 14х² + 25х - 84 = 0

3. Решите неравенство и найдите его наименьшее целочисленное решение.

4. Электронный завод получил заказ на изготовление 300 новых электронных игр. Изготавливая в день на 10 игр больше запланированного, завод выполнил заказ на 1 день раньше срока. Сколько электронных игр в день изготавливал завод?

5. Дана функция у = f (x) , где f(x) =. Найдите f (x - 5), если

Кодификатор

№ умения

Проверяемое умение

№ задания

Уметь строить и исследовать квадратичную функцию

Уметь решать квадратное уравнение

Уметь решать линейное неравенство

Уметь решать задачи на производительность труда

Уметь находить значение функции

Геометрия - 8.

Контрольная работа № 1

Вариант 1

1^о. Диагонали прямоугольника CDEF пересекаются в точке О. Найдите угол между диагоналями, если  СDO = 40⁰.

2^о. Найдите боковую сторону равнобедренной трапеции, основания которой равны 12см и 6см, а один из углов равен 60⁰.

3^о. На продолжении диагонали АС прямоугольника ABCD отложены равные отрезки АМ и СN. Докажите: а) что треугольники MAD и NCB равны; б) что четырехугольник MBND параллелограмм.

Контрольная работа № 1

Вариант 2

1^о. Диагонали ромба ABCD пересекаются в точке О. Найдите углы треугольника АОВ, если между диагоналями, если  ВСD = 75⁰.

2^о. Найдите меньшую боковую сторону прямоугольной трапеции, основания которой равны 10см и 6см, а один из углов равен 45⁰.

3^о. На диагонали NK прямоугольника MNPK отложены равные отрезки NА и KE. Докажите: а) что треугольники ANP и EKM равны; б) что четырехугольник APEM параллелограмм.

Кодификатор

№ умения

Проверяемое умение

№ задания

Уметь находить углы в ромбе

Уметь находить стороны в трапеции

Уметь доказывать равенство треугольников

Контрольная работа № 2

Вариант 1

1^о. Смежные стороны параллелограмма равны 12см и 20см, а один из его углов равен 30⁰. Найдите площадь параллелограмма.

2^о. Найдите периметр прямоугольника, если его диагональ равна 15см, а одна из сторон - 9см.

3^о. Площадь прямоугольной трапеции равна 120см², а ее высота равна 8см. Найти все стороны трапеции, если одно из оснований больше другого на 6см.

Контрольная работа № 2

Вариант 2

1^о. Высота BD треугольника АВС делит основание АС на отрезки: AD = 8см, DC = 12см, а угол А при основании равен 45⁰. Найдите площадь этого треугольника.

2^о. Найдите периметр прямоугольного треугольника, если его катеты равны 12см и 16см.

3^о. Найти площадь трапеции CDEF c основаниями CF и DE, если CD = 12см, DE = 14cм, CF = 30см,  D = 150⁰.

Кодификатор

№ умения

Проверяемое умение

№ задания

Уметь находить площадь параллелограмма и треугольника

Уметь находить периметр прямоугольника

Уметь находить площадь трапеции

Контрольная работа № 3

Вариант 1

1^о. Высота CD прямоугольного треугольника АВС делит гипотенузу АВ на части AD = 16см и BD = 9см. Докажите, что ∆ ACD ∞ ∆ CBD.

2^о. АВ || CD. Найдите АВ, если OD = 15см, OB = 9см, CD = 25см.

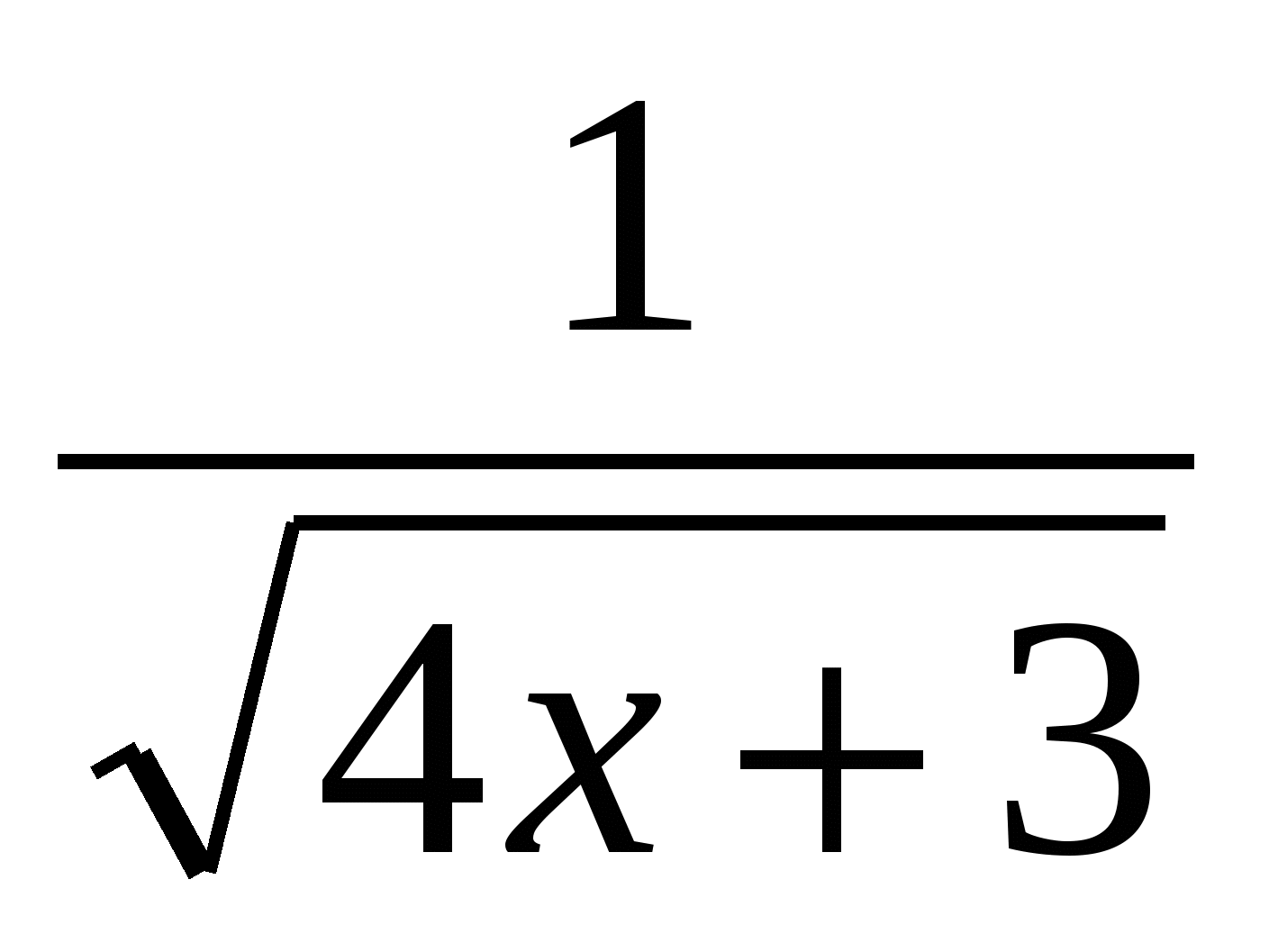
3. Найти отношение площадей треугольников АВС и KMN, если АВ = 8см, ВС = 12см, АС = 16см, КМ = 10см, MN = 15см, NK = 20cм.

Контрольная работа № 3

Вариант 2

1^о. Высота CD прямоугольного треугольника АВС отсекает от гипотенузы АВ, равной 9см, отрезок AD = 4см. Докажите, что ∆ AВC ∞ ∆ АCD.

2^о. MN || DF. Найдите MN, если DM = 6см, EM = 8см, DF = 21см.

3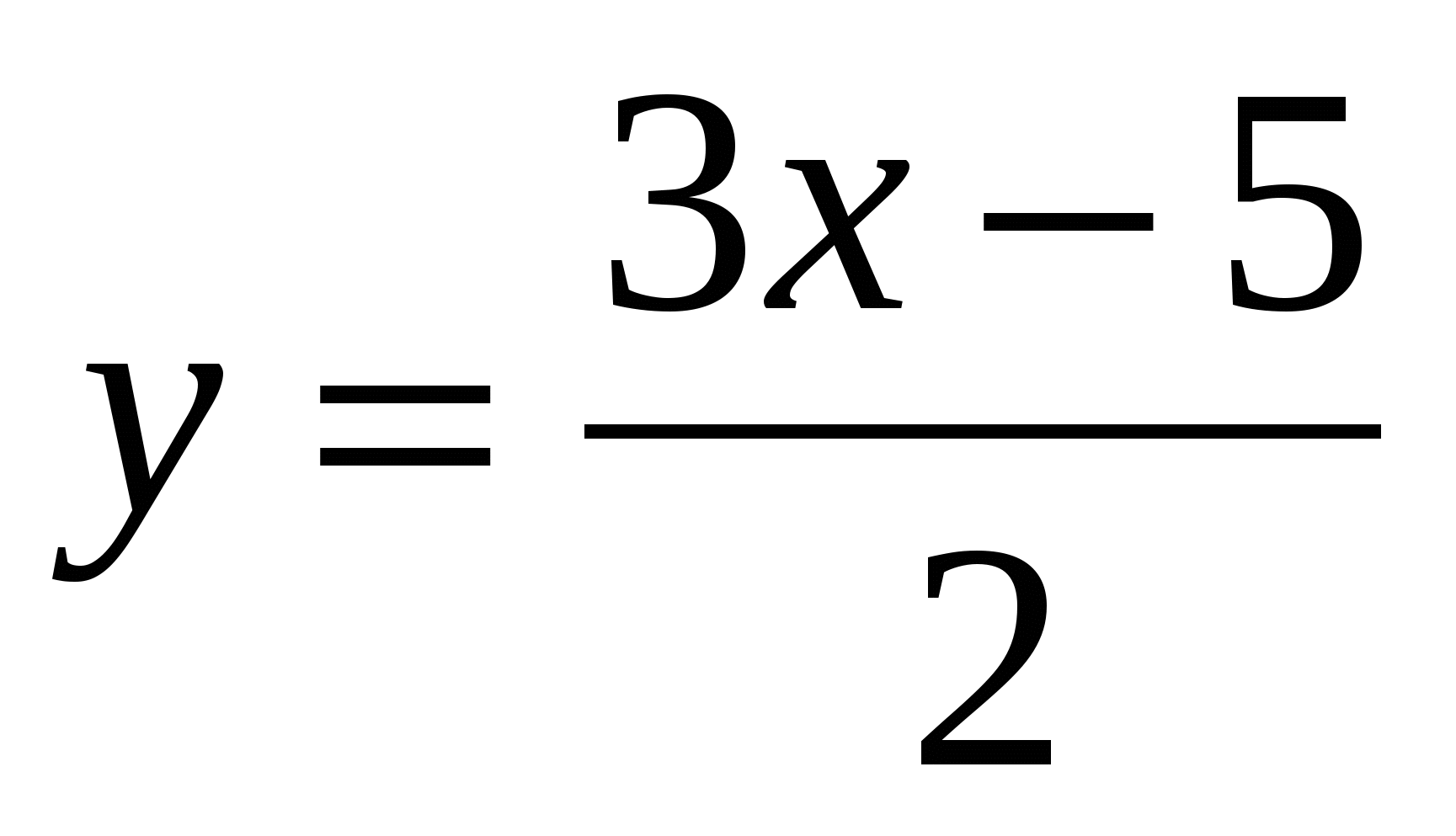. Даны стороны треугольников АВС и DEF, если АВ = 12см, ВС = 15см, АС = 21см, DE = 16см, EF = 20см, DF = 28cм. Найти отношение площадей этих треугольников.

Кодификатор

№ умения

Проверяемое умение

№ задания

Уметь доказывать подобие треугольников

Уметь находить стороны параллелограмма

Уметь находить отношение площадей подобных треугольников

Контрольная работа № 4

Вариант 1

1. Площадь ромба равна 48см². Найти площадь четырехугольника, вершинами которого являются середины сторон данного ромба.

2. В равнобедренной трапеции меньшее основание равно 4см, боковая сторона равна 6см, а один из углов равен 120⁰. Найти площадь трапеции.

3. В прямоугольном треугольнике АВС А = 90⁰, АВ = 20см,высота AD = 12см. Найти АС и cos C.

Контрольная работа № 4

Вариант 2

1. Площадь прямоугольника равна 36см². Найти площадь четырехугольника, вершинами которого являются середины сторон данного прямоугольника.

2. В прямоугольной трапеции меньшее основание равно 3см, большая боковая сторона равна 4см, а один из углов равен 150⁰. Найти площадь трапеции.

3. Высота BD прямоугольного треугольника АВС равна 24см и отсекает от гипотенузы АС отрезок DC, равный 18см. Найти АВ и cos А.

Кодификатор

№ умения

Проверяемое умение

№ задания

Уметь находить площадь параллелограмма

Уметь находить площадь трапеции

Уметь находить элементы прямоугольного треугольника

Контрольная работа № 5

Вариант 1

1. Диагонали ромба АВСD пересекаются в точке О. Докажите, что прямая BD касается окружности с центром А и радиусом, равным ОС.

2^о. Центр описанной окружности лежит на высоте равнобедренного треугольника и делит высоту на отрезки, равные 5см и 13см. Найти площадь этого треугольника.

3^о. Основание равнобедренного треугольника равно 18см, а боковая сторона равна 15см. Найти радиусы вписанной в треугольник и описанной около треугольника окружностей.

Контрольная работа № 5

Вариант 2

1. В равнобедренном треугольнике АВС с основанием АС проведена медиана BD. Докажите, что прямая BD касается окружности с центром С и радиусом, равным AD.

2^о. Меньший из отрезков, на которые центр описанной около равнобедренного треугольника окружности делит его высоту , равен 8см, а основание треугольника равно 12см. Найти площадь этого треугольника.

3^о. Высота, проведенная к основанию равнобедренного треугольника, равно 9см, а само основание равно 24см. Найти радиусы вписанной в треугольник и описанной около треугольника окружностей.

Кодификатор

№ умения

Проверяемое умение

№ задания

Уметь доказывать, что прямая является касательной

Уметь находить площадь вписанного треугольника

Уметь находить радиусы вписанной и описанной окружности

Контрольная работа № 6

Вариант 1

1. Начертите два неколлинеарных вектора так, что | | = 3cм, | | = 2см. Постройте вектор

2. Точка К делит отрезок MN в отношении MK : KN = 3 : 2. Выразите вектор через векторы и , где А - произвольная точка.

3. Высота, проведенная из вершины тупого угла равнобедренной трапеции, делит большее основание трапеции на два отрезка, меньший из которых равен 2см. Найдите большее основание трапеции, если ее средняя линия равна 8см.

Контрольная работа № 6

Вариант 2

1. Начертите два неколлинеарных вектора так, что | | = 3cм, | | = 3м. Постройте вектор

2.Точка А делит отрезок EF в отношении ЕА : AF = 2 : 5. выразите вектор через векторы и , где К- произвольная точка.

3. Высота, проведенная из вершины тупого угла равнобедренной трапеции, делит среднюю линию на отрезки, равные 2см и 6см. Найдите основания трапеции.

Кодификатор

№ умения

Проверяемое умение

№ задания

Уметь строить вектор способом сложения

Уметь выражать вектор через два других

Уметь решать задачи векторным способом

Календарно-тематическое планирование учебного материала по алгебре /8 класс/

№

Тема урока

Кол-во.часов

Дата

Тип урока

Содержание

Цель урока

Повторение

УУД

Диагностика

Примечание

Повторение курса 7класса (5ч)

Основная цель: - формирование представлений о целостности и непрерывности курса алгебры 7 класса;

- овладение умением обобщения и систематизации знаний учащихся по основным темам курса алгебры 7 класса;

- развитие логического, математического мышления и интуиции, творческих способностей.

Свойства степени с натуральным показателем

Частично-поисковый

Свойства степени с натуральным показателем, действия со степенями одинакового основания

основные свойства степени с натуральным показателем; свойства при решении задач.

Регулятивные УУД:

Умение самостоятельно находить и излагать нужную информацию

Формулы сокращенного умножения

Проблемное изложение

Квадрат суммы, квадрат разности, разность квадратов, разность и сумма кубов, разложение на множители по формулам сокращенного умножения

преобразования многочленов, применяя формулы сокращенного умножения

Регулятивные УУД:

Умение самостоятельно находить и излагать нужную информацию

С.р.

Функция ее свойства и график

Комбинированный

Функция ее свойства и график, графическое решение уравнения

описание геометрических свойств параболы, нахождение наибольшего и наименьшего значения функции на заданном отрезке, точки пересечения параболы с графиком линейной функции

Регулятивные УУД:

Умение самостоятельно находить и излагать нужную информацию

Тестовые задания

Уч.диск «математика 5-11»

Системы линейных уравнений

комбинированный

Алгоритмы решения

Алгоритмы решения: графический, подстановки, сложения.

Регулятивные УУД:

Умение самостоятельно находить и излагать нужную информацию

С.р.

Входная контрольная работа

Контроль сформированных за 7 класс знаний, умений и навыков, применение их на практике

Регулятивные УУД:

уметь принимать решения, брать на себя ответственность за их последствия

Глава 1: Алгебраические дроби (20ч).

Основная цель: - формирование представлений о многочлене от одной переменной, алгебраической дроби, о рациональном выражении;

- формирование умений разложения многочлена на множители, сокращения дробей, приведения алгебраических дробей к общему знаменателю;

- овладение умением упрощения выражений, сложения, вычитания, умножения и деления алгебраических дробей с разными знаменателями;

- овладение навыками преобразования рациональных выражений, доказательства тождеств, решения рациональных уравнений способом освобождения от знаменателей с составлением математической модели реальной ситуации

Основные понятия

1Комбинированный

Алгебраическая дробь; значения алгебраической дроби; допустимых значений для дроби; область допустимых значений

Ввести понятие алгебраической дроби и допустимых значений для дроби; формировать умение определять область допустимых значений для дроби; сформировать умение составлять математические модели для задач.

Алгебраическая дробь, числитель и знаменатель дроби

Регулятивные УУД:

самостоятельно искать, систематизировать, анализировать и отбирать необходимую для решения задач информацию.

Основное свойство алгебраической дроби (О.С.Д.)

1Комбинированный

2Поисковый

Основное свойство алгебраической дроби, сокращение дробей, приведение А.Д. к общему знаменателю

Рассмотреть О.С.Д. для алгебраич. дробей; сформировать умение сокращать дроби и приводить дроби к наименьшему общему знаменателю

Основное свойство дроби

Регулятивные УУД:

организовывать планирование, анализ, рефлексию, самооценку своей познавательной деятельности

Обучающая с.р.

Сложение и вычитание А.Д. с одинаковыми знаменателями

1Комбинированный

2учебный практикум

А.Д., алгоритм сложения (вычитания) А.Д. с одинаковыми знаменателями

Объяснить правила сложения и вычитания А.Д. с одинаковыми знаменателями; формировать умение выполнять действия сложения и вычитания с А.Д.

Правила сложения и вычитания числовых дробей

Регулятивные УУД:

Организовывать планирование, анализ, рефлексию, самооценку своей учебно-познавательной деятельности

Обучающая с.р.

Сложение и вычитание А.Д. с разными знаменателями

1Комбинированный

2Поисковый

3Учебный практикум

Упрощение выражений, сложение и вычитание А.Д. с разными знаменателями, наименьший общий знаменатель, правило приведения А.Д. к общему знаменателю, дополнительный

Объяснить правила сложения и вычитания А.Д. с разными знаменателями; формировать умение выполнять действия сложения и вычитания с А.Д.

Правила сложения и вычитания числовых дробей; правила сложения и вычитания А.Д. с одинаковыми знаменателями

Коммуникативные УУД: владение способами совместной деятельности в группе, умение искать и находить компромиссы

Обучающая с.р., тестовая работа

Контрольная работа №1 « Сложение и вычитание А.Д»

Контроль, оценка и коррекция знаний

Контроль ОУУН по теме« Сложение и вычитание А.Д»

Регулятивные УУД:

уметь принимать решения, брать на себя ответственность за их последствия

Умножение и деление А.Д. Возведение А.Д. в степень

1Поисковый

2Комбинированный

Умножение и деление А.Д., возведение А.Д. в степень, преобразование выражений, содержащих А.Д.

Объяснить правила умножения и деления вычитания А.Д.; объяснить правила возведения в степень А.Д.; развивать умения выполнять действия с А.Д.

Правила умножения и деления числовых дробей

Регулятивные УУД:

Преобразование рациональных выражений

1Проблемный

2Поисковый

3Комбинированный

Рациональные выражения, преобразование рациональных выражений, доказательства тождеств

Объяснить правила преобразования рациональных выражений, развивать умение упрощать выражения, доказывать тождества

Формулы сокращенного умножения, правила сложения и вычитания, умножения и деления А.Д. с разными знаменателями;

Регулятивные УУД:

Умение излагать информацию, обосновывая собственный подход, развернуто обосновывать суждения

Обучающая с.р., тестовая работа

Первые представления о рациональных уравнениях

1Комбинированный

2Учебный практикум

Рациональное уравнение, способ освобождения от знаменателей, составление математической модели

Объяснить правила решения рациональных уравнений, формировать умения решать уравнения

Алгоритм решения линейных уравнений

Регулятивные УУД:

организовывать планирование, анализ, рефлексию, самооценку своей познавательной деятельности

Степень с отрицательным целым показателем

1Комбинированный

2Проблемное изложение

Степень с отрицательным целым показателем, умножение, деление и возведение степени в степень

Ввести понятие и свойства степени с отрицательным целым показателем, формировать умение работать со степенями с целым показателем

Свойства степени с натуральным показателем

Регулятивные УУД:

Обучающая с.р., тестовая работа

Подготовка к контрольной работе

1Обобщение и систематизация знаний

Систематизировать и обобщить знания о

выполнении действий с А.Д., решении уравнений и задач

Регулятивные УУД:

Контрольная работа №2 «Алгебраические дроби»

Контроль, оценка и коррекция знаний

Контроль ОУУН по теме« Алгебраические дроби »

Регулятивные УУД:

уметь принимать решения, брать на себя ответственность за их последствия

Глава: Функция. Свойства квадратного корня (18ч).

Основная цель: - формирование представлений о квадратном корне из неотрицательного числа, о функции;

- формирование умений построения графика функции и описания ее свойств, использования алгоритма извлечения квадратного корня;

- овладение умением преобразовывать выражения, содержащие операцию извлечения квадратного корня, применяя свойства квадратных корней;

- овладение навыками решения уравнений, содержащих радикал

Множество рациональных чисел

1Комбинированный

Множество рациональных чисел, знак принадлежности, знак включения, символы математического языка, бесконечные десятичные периодические дроби, период, чисто периодическая дробь, смешанно периодическая дробь

Ввести понятие множества натуральных, действительных, рациональных чисел, формировать умение различать множества чисел

Натуральные, целые, обыкновенные и десятичные дроби, положительные, отрицательные числа

Регулятивные УУД:

работа с различными источниками информации

Понятие квадратного корня из неотрицательного числа

1Комбинированный

2Учебный практикум

Квадратный корень, квадратный корень из неотрицательного числа, подкоренное выражение, извлечение квадратного корня, кубический корень из неотрицательного числа, корень n-й степени из неотрицательного числа

Ввести понятие квадратного корня, рассмотреть правила вычисления корня из неотрицательного числа, формировать умение вычислять квадратный корень из чисел и выражений

Свойства степени, порядок выполнения действий

Регулятивные УУД:

организовывать планирование, анализ, рефлексию, самооценку своей познавательной деятельности

С.р.

Иррациональные числа

1Проблемное изложение

Иррациональные числа, бесконечная десятичная непериодическая десятичная дробь иррациональные выражения

Ввести понятие иррациональных чисел, развивать умение различать множества чисел

понятия натуральных, действительных, рациональных чисел, перевод периодических дробей в обыкновенные дроби

Регулятивные УУД:

Организовывать планирование, анализ, рефлексию, самооценку своей учебно-познавательной деятельности

Множество действительных чисел

1Проблемное изложение

Множество действительных чисел, сегмент первого ранга, сегмент второго ранга, взаимно однозначное соответствие, сравнение действительных чисел, действия над действительными числами

Ввести понятие и обозначение множества действительных чисел

понятия натуральных, действительных, рациональных, иррациональных чисел

Коммуникативные УУД:

владение способами совместной деятельности в группе, умение искать и находить компромиссы

Функция, её свойства и график

1Проблемное изложение

2Учебный практикум

Функция, график, свойства, функция выпуклая вверх, функция выпуклая вниз

Ввести функцию и показать правила построения графика данной функции, ввести понятие выпуклости и области значения, формировать умение строить графики функций вида, и по графику определять свойства функции

понятие квадратного корня, правила вычисления корня из неотрицательного числа, правила

построения графика функции если известен график функции

Регулятивные УУД:

Умение анализировать образовательную ситуацию, формулировать выводы, осуществлять их проверку

Свойства квадратных корней

1Комбинированный

2Поисковый

Квадратный корень из произведения, квадратный корень из дроби, вычисление корней

Доказать свойства квадратных корней и показать их применение, формировать умение вычислять квадратные корни

Разность квадратов, основное свойство дроби

Регулятивные УУД:

организовывать планирование, анализ, рефлексию, самооценку своей познавательной деятельности

С.р.

Преобразование выражений, содержащих операцию извлечения квадратного корня

1Комбинированный

2Поисковый

3Проблемный

4Исследовательский

Преобразование выражений, содержащих операцию извлечения квадратного корня, освобождение от иррациональности в знаменателе

Объяснить правила вынесения множителя из-под знака корня, внесения множителя под знак корня, преобразования подобных членов, рассмотреть примеры на преобразование различной сложности, развивать умение пользоваться свойствами квадратных корней

Повторить свойства квадратных корней

Регулятивные УУД:

Владеть способами самоопределения в ситуациях выбора на основе собственных позиций

Обучающая с.р., тестовая работа

Подготовка к контрольной работе

1Обобщение и систематизация знаний

Развивать умение упрощать выражения, 3вычислять квадратные корни, решать уравнения

Понятие квадратного корня и его свойства

Регулятивные УУД:

Контрольная работа №3 «ФункцияСвойства квадратного корня»

Контроль, оценка и коррекция знаний

Контроль ОУУН по теме «ФункцияСвойства квадратного корня»

Регулятивные УУД:

уметь принимать решения, брать на себя ответственность за их последствия

Модуль действительного числа

1Комбинированный

2Учебный практикум

Модуль действительного числа, свойства модулей, геометрический смысл модуля действительного числа, совокупность уравнений, тождество

Ввести понятие модуль действительного числа, рассмотреть свойства и разъяснить геометрический смысл модуля, ввести функцию, правила построения графиков, содержащих функцию, правила решения и оформления уравнений, содержащих модуль

Понятие модуля числа, обозначение модуля

Регулятивные УУД:

организовывать планирование, анализ, рефлексию, самооценку своей познавательной деятельности

С.р.

Глава: Квадратичная функция. Функция (18ч). Основная цель: - формирование представлений о функции , функции, гиперболе, перемещении графика по координатной плоскости, квадратичной функции ;

- формирование умений построения графиков функций ,, и описание их свойств;

- овладение умением использования алгоритма построения графика функции ,

- овладение навыками решения квадратных уравнений графическим способом, построения графика дробно-линейной функции

Функция ²,ее свойства и график

1Комбинированный

2Поисковый

Кусочно-заданные функции, контрольные точки график, парабола, вершина параболы, ось симметрии параболы, фокус параболы, свойства функции, ее график

Объяснить свойства функции и показать построение графика данной функции, формировать умение строить графики функций и , и по графику определять свойства данных функций, ввести правила решения уравнений графическим способом, показать способ построения графиков функций, заданных несколькими условиями

Свойства функций и, их графики

Регулятивные УУД:

организовывать планирование, анализ, рефлексию, самооценку своей познавательной деятельности

Практическая работа

Функция , ее свойства и график

1Комбинированный

2Учебный практикум

Функция. Гипербола, ветви гиперболы, асимптоты, ось симметрии гиперболы, Функция , ее свойства и график, обратная пропорциональность, коэффициент обратной пропорциональности, область значений функции, окрестность точки, точка максимума, точка минимума

Ввести понятие гиперболы, показать правила построения графика функции и рассмотреть свойства, развивать умение строить графики известных функций

Алгоритм графического решения уравнений и систем уравнений

Регулятивные УУД:

Владеть способами самоопределения в ситуациях выбора на основе собственных позиций

Практическая работа

Контрольная работа №4 « Квадратичная функция. Функция »

Контроль, оценка и коррекция знаний

Контроль ОУУН по теме «Квадратичная функция. Функция »

уметь принимать решения, брать на себя ответственность за их последствия

Как построить график функции, если известен график функции

1Проблемный

2Поисковый

Параллельный перенос, параллельный перенос вправо (влево), вспомогательная система координат, алгоритм построения графика функции

Объяснить правила построения графика функции, если известен график функции, формировать умение строить графики различных функций

Правила построения параболы и гиперболы

Регулятивные УУД:

задавать вопросы к наблюдаемым фактам, отыскивать причины явлений, обозначать свое понимание или непонимание по отношению изучаемой проблеме

Практическая работа

Как построить график функции если известен график функции

1Проблемный

2Поисковый

Параллельный перенос, параллельный перенос вверх (вниз), алгоритм построения графика функции вспомогательная система координат

Правило построения графика функции если известен график функции формировать умение строить графики различных функций

Правило построения графика функции

Познавательные УУД: задавать вопросы к наблюдаемым фактам, отыскивать причины явлений, обозначать свое понимание или непонимание по отношению изучаемой проблеме.

Практическая работа

Как построить график функции если известен график функции2

1Проблемный

2Поисковый

Параллельный перенос, параллельный перенос вправо (влево), параллельный перенос вверх (вниз), алгоритм построения графика функции вспомогательная система координат

Объяснить правило построения графика функции если известен график функции формировать умение строить графики различных функций, решение уравнений графическим способом

Правила

построения графика функции , если известен график функции, правило выделения квадрата двучлена

Познавательные УУД: задавать вопросы к наблюдаемым фактам, отыскивать причины явлений, обозначать свое понимание или непонимание по отношению изучаемой проблеме

Практическая работа

Функция ее свойства и график

1Комбинированный

2Поисковый

3Учебный практикум

Функция , квадратичная функция, график квадратичной функции, ось параболы, формула абсциссы параболы, направление ветвей параболы, алгоритм построения графика

Ввести алгоритм построения графика функции, рассмотреть свойства данной функции, формировать умение строить график данной функции

Правила

построения графика функции , если известен график функции,

Регулятивные УУД:

организовывать планирование, анализ, рефлексию, самооценку своей познавательной деятельности

Практическая работа

Графическое решение квадратных уравнений

1Комбинированный

2Учебный практикум

Квадратное уравнение, несколько способов графического решения уравнения

Формировать умение решать квадратные уравнения графическим способом

Правила

построения графика функции , если известен график функции

Регулятивные УУД:

С.р.

Подготовка к контрольной работе

1Обобщение и систематизация знаний

Закрепить умение построения графиков различных функций, умение решать уравнения и системы уравнений графическим способом

Регулятивные УУД:

Контрольная работа №5 «Квадратичная функция»

Контроль, оценка и коррекция знаний

Контроль ОУУН по теме« Квадратичная функция»

Регулятивные УУД:

уметь принимать решения, брать на себя ответственность за их последствия

Глава 4: Квадратные уравнения (23ч)

Основная цель: - формирование представлений о полном, приведенном, неполном квадратном уравнении, дискриминант квадратного уравнения, формулах корней квадратного уравнении, теореме Виета;

- формирование умений решить приведенное квадратное уравнение, применяя обратную теорему Виета;

- овладение умением разложения квадратного трехчлена на множители, решения квадратного уравнения по формулам корней;

- овладение навыками решения рационального и иррационального уравнения как математической модели реальных ситуаций

Основные понятия

1Поисковый

2Комбинированный

Квадратное уравнение, старший коэффициент, второй коэффициент, свободный член, приведенное квадратное уравнение полное квадратное уравнение, корень квадратного уравнения, решение квадратного уравнения

Ввести понятие квадратного уравнения, корня квадратного уравнения, показать решения квадратных уравнений, правила решения неполных квадратных уравнений

Формулы сокращенного умножения, понятие квадратного корня и его свойства

Регулятивные УУД:

Умение самостоятельно искать и отбирать необходимую для решения учебных информацию

С.р.

Формулы корней квадратного уравнения

1Комбинированный

2Поисковый

3Учебный практикум

Дискриминант квадратного уравнения, формулы корней квадратного уравнения, правило решения квадратного уравнения

Показать способ решения полных квадратных уравнений с использованием формулы корней квадратного уравнения, формировать умения решать квадратные уравнения

понятие квадратного уравнения, корня квадратного уравнения, алгоритм решения квадратных уравнений, правила решения неполных квадратных уравнений

Регулятивные УУД:

Умение анализировать образовательную ситуацию, формулировать выводы, осуществлять их проверку

Обучающая с.р., тестовая работа

Рациональные уравнения

1Комбинированный

2Поисковый

3Учебный практикум

Рациональные уравнения, алгоритм решения рационального уравнения, проверка корней уравнения, посторонние корни

Выработать алгоритм решения рациональных уравнений, формировать умение решать рациональные уравнения, рассмотреть решение рациональных уравнений различного уровня сложности

Понятие А.Д., допустимые значения переменных, формулы корней квадратного уравнения, правило решения квадратного уравнения

Регулятивные УУД:

Организовывать планирование, анализ, рефлексию, самооценку своей учебно-познавательной деятельности

Обучающая с.р., тестовая работа

Подготовка к контрольной работе

1Обобщение и систематизация знаний

Повторить понятие квадратного уравнения, различные способы решения квадратных уравнений

Формулы корней квадратного уравнения, правило решения квадратного уравнения

Регулятивные УУД:

Контрольная работа №6 «Решение квадратных уравнений»

Контроль, оценка и коррекция знаний

Контроль ОУУН по теме «Решение квадратных уравнений»

Регулятивные УУД:

уметь принимать решения, брать на себя ответственность за их последствия

Рациональные уравнения как математические модели реальных ситуаций

1Комбинированный

2Поисковый

3Учебный практикум

4Учебный практикум

Рациональные уравнения, математическая модель реальной ситуации, решение задач на составление уравнений

Объяснить правила оформления решения задач с помощью рациональных уравнений, формировать умение решать и оформлять задачи

Понятие А.Д., допустимые значения переменных

Регулятивные УУД:

организовывать планирование, анализ, рефлексию, самооценку своей познавательной деятельности

Обучающая с.р., тестовая работа

Ещё одна формула корней квадратного уравнения

1Поисковый

2Комбинированный

Формулы для решения квадратных уравнений с четным вторым коэффициентом

Вывести формулы для решения квадратных уравнений с четным вторым коэффициентом

Формулы корней квадратного уравнения

Коммуникативные УУД: владение способами совместной деятельности в группе, умение искать и находить компромиссы

С.р

Теорема Виета

1Комбинированный

2Учебный практикум

Теорема Виета, обратная теорема Виета, симметрическое выражение с двумя переменными

Доказать теорему Виета, показать ее применение, рассмотреть различные задания на применение теоремы, развивать умение решать квадратные уравнения различными способами, раскладывать многочлены на множители, сокращать дроби

Формулы корней квадратного уравнения

Регулятивные УУД:

Ставить познавательные задачи и выдвигать гипотезы, описывать результаты, формулировать выводы

С.р.

Иррациональные уравнения

1Проблемный

2Комбинироавнный

3Учебный практикум

Иррациональные уравнения, метод возведения в квадрат, проверка корней, равносильные уравнения, равносильные преобразования уравнений, неравносильные преобразования уравнений

Ввести понятие иррациональных уравнений, равносильных уравнений, объяснить правило решения иррациональных уравнений и показать оформление решения, формировать умение решать иррациональные уравнения

Алгоритм решения линейных рациональных, квадратных уравнений

Регулятивные УУД:

Работать с инструкциями, владеть навыками работы с различными источниками информации

Обучающая с.р., тестовая работа

Подготовка к контрольной работе

1Обобщение и систематизация знаний

Повторить понятие квадратного уравнения, различные способы решения квадратных, рациональных и иррациональных уравнений

Формулы корней квадратного уравнения, правило решения квадратного уравнения, правило решения рациональных и иррациональных уравнений

Регулятивные УУД:

Контрольная работа №7 «Квадратные уравнения»

Контроль, оценка и коррекция знаний

Контроль ОУУН по теме«Квадратные уравнения»

Регулятивные УУД:

уметь принимать решения, брать на себя ответственность за их последствия

Глава 5: Неравенства (14ч)

Основная цель: - формирование представлений о числовых неравенствах, неравенстве с одной переменной, модуле действительного числа;

- формирование умений исследования функции на монотонность, применения приближенных вычислений;

- овладение умением построения графика функции модуль, описания ее свойств;

- овладение навыками решения линейных, квадратных неравенств, решения неравенств, содержащих переменную величину под знаком модуль

Свойства числовых неравенств

1Комбинированный

2Поисковый

Числовое неравенство, свойства числовых неравенств, неравенства одинакового смысла, неравенства противоположного смысла, среднее арифметическое, среднее геометрическое, неравенство Коши

Ввести свойства числовых неравенств, формировать умение сравнивать числа и выражения, умение пользоваться свойствами неравенств

Правила сравнения чисел, строгое, нестрогое числовое неравенство

Регулятивные УУД:

Ставить познавательные задачи и выдвигать гипотезы, описывать результаты, формулировать выводы

Решение линейных неравенств

1Комбинированный

2Учебный практикум

3Исследовательский

Неравенство с переменной, решение неравенства с одной переменной, множество решений, система линейных неравенств, пересечение решений неравенств системы

Объяснить правило решения и оформления линейных неравенств, формировать умение решать линейные неравенства и показывать решение на координатной прямой

Аналитическая, символическая, геометрическая записи числовых промежутков

Регулятивные УУД:

Работать с инструкциями, владеть навыками работы с различными источниками информации

Обучающая с.р., тестовая работа

Исследование функций на монотонность

1Комбинированный

2Проблемное изложение

Возрастающая функция на промежутке, убывающая функция на промежутке, линейная функция, функция,, монотонная функция

Понятие убывающей и возрастающей функций, формировать умение определять какой (возрастающей или убывающей) является функция

функции, ,,их свойства и графики

Регулятивные УУД:

С.р.

Решение квадратных неравенств

1Комбинированный

2Поисковый

3Учебный практикум

Квадратное неравенство, знак объединения множеств, алгоритм решения квадратных неравенств, метод интервалов

Правило решения квадратных неравенств, формировать умения решать различные неравенства, развивать умение решать неравенства различными способами

Алгоритм построения параболы, правила решения квадратных уравнений

Регулятивные УУД:

Организовывать планирование, анализ, рефлексию, самооценку своей учебно-познавательной деятельности

Обучающая с.р., тестовая работа

Контрольная работа №8 «Неравенства»

Контроль, оценка и коррекция знаний

Проверка ОУУН по теме «Неравенства»

Регулятивные УУД:

уметь принимать решения, брать на себя ответственность за их последствия

Приближенные значения действительных чисел

1Частично-поисковый

Приближенное значение по недостатку, приближенное значение по избытку, округление чисел, погрешность, абсолютная погрешность, правило округления чисел, относительная погрешность

Правила приближенного вычисления, формировать умение находить значения выражений

Графический способ решения уравнений

Стандартный вид положительного числа

1Комбинированный

2Частично-поисковый

Стандартный вид положительного числа, порядок числа, запись числа в стандартном виде

Ввести понятие стандартного вида числа, показать правила преобразования числа в стандартный вид, формировать умение приводить число к стандартному виду

Свойства степени с отрицательным целым показателем

Регулятивные УУД:

Умение самостоятельно искать и отбирать необходимую для решения учебных информацию

С.р.

Обобщающее повторение (4ч)

Основная цель: - формирование представлений о - формирование умений - овладение умением - овладение навыками

Алгебраические дроби

1Учебный практикум

Преобразование рациональных выражений, решение рациональных уравнений

Правила выполнения действий с алгебраическими дробями, рассмотреть различные примеры на упрощение выражений различной сложности

Регулятивные УУД:

Ставить познавательные задачи и выдвигать гипотезы, описывать результаты, формулировать выводы

Тестовая работа

Квадратные уравнения

1Учебный практикум

Формулы корней квадратного уравнения, теорема Виета, разложение квадратного трехчлена

на множители

Правила решения линейных, квадратных, рациональных, иррациональных уравнений, решение задач различного уровня сложности

Тестовая работа

Неравенства

1Учебный практикум

Решение линейных и квадратных неравенств, исследование функции на монотонность

Понятие неравенства, виды неравенств, способы их решения

Тестовая работа

Итоговая контрольная работа

Контроль, оценка и коррекция знаний

Проверить ОУУН по курсу 8 класса

Регулятивные УУД:

уметь принимать решения, брать на себя ответственность за их последствия

Календарно-тематическое планирование учебного материала по геометрии /8 класс/

№

Тема урока

Кол-во часов

Дата

Содержание

Цель урока

Повторение

УУД

Диагностический инвентарей

Примечание

Вводное повторение.

Основные понятия, виды треугольников их свойства, признаки и свойства // прямых

Повторить наиболее важные темы 7 класса, совершенствовать навыки решения задач.

Признаки равенства треугольников, соотношения между углами и сторонами треугольника, свойства р/б Δ, п/у Δ, признаки и свойства // прямых, задачи на построения.

Регулятивные УУД:

Владеть способами самоопределения в ситуациях выбора на основе собственных позиций

Тестовая работа

Входная контрольная работа

Контроль сформированных за 7 класс знаний, умений и навыков, применение их на практике

Регулятивные УУД:

уметь принимать решения, брать на себя ответственность за их последствия

Глава 5. Четырехугольники. (14 ч)

Основная цель: дать учащимся систематические сведения о четырёхугольниках и их свойствах; сформировать представления о фигурах, симметричных относительно точки или прямой, развивать навыки использования чертёжных инструментов, построения и измерения фигур; формировать геометрическую культуру, логическое мышление, математическую речь.

Многоугольники.

Многоугольник, выпуклый многоугольник, четырехугольник, сумма углов выпуклого n- угольника.

Ввести понятие многоугольника, выпуклого многоугольника и рассмотреть четырёхугольник как частный вид многоугольника. Вести формулу суммы углов выпуклого многоугольника и суммы углов четырёхугольника. Научить решать задачи.

Понятие суммы углов фигуры, сумма углов треугольника, понятие биссектрисы

Регулятивные УУД:

Ставить цель и организовывать её достижение, меть пояснить свою цель

С.р. обучающего характера

Параллелограмм. Признаки параллелограмма. Решение задач по теме «Параллелограмм».

Параллелограмм, свойства и признаки параллелограмма,

Ввести понятие параллелограмма и рассмотреть его свойства. Изучить признаки параллелограмма. Научить применять свойства и признаки параллелограмма при решении задач. Совершенствовать навыки решения задач.

признаки и свойства // прямых, признаки равенства треугольников

Регулятивные УУД:

Организовывать планирование, анализ, рефлексию, самооценку своей учебно- познавательной деятельности

С.р.

презентация

Трапеция.

Трапеция, равнобедренная и прямоугольная трапеции

Ввести понятие трапеции и ее элементов, познакомить учащихся с равнобедренной и прямоугольной трапециями. Рассмотреть некоторые свойства равнобедренной трапеции. Учить применять полученные знания в процессе решения задач.

признаки и свойства // прямых, признаки равенства треугольников

Регулятивные УУД:

Задавать вопросы к наблюдаемым фактам, отыскивать причины явлений, обозначать своё понимание или непонимание по отношению к изучаемой проблеме

Теорема Фалеса. Задачи на построение.

Теорема Фалеса. Деление данного отрезка на n равных частей.

Рассмотреть теорему Фалеса и закрепить ее в процессе решения задач. Совершенствовать навыки решения задач на применении свойств равнобедренной трапеции, ее признаков, знаний по теме «Трапеция». Совершенствовать навыки решения задач на построение. Научить делить данный отрезок на n равных частей.

Параллелограмм, трапеция, признаки и свойства // прямых, признаки равенства треугольников

Регулятивные УУД:

Ставить познавательные задачи и выдвигать гипотезы; владеть измерительными навыками; использовать элементы вероятностных и статистических методов познания

Практ.работа

Прямоугольник.

Прямоугольник, свойство диагоналей прямоугольника

Рассмотреть свойства прямоугольника как частного вида параллелограмма и научить применять их в процессе решения задач.

Понятие прямоугольника. Параллелограмм, трапеция, признаки и свойства // прямых, признаки равенства треугольников

Регулятивные УУД:

Уметь принимать решения, брать на себя ответственность за их последствия

Ромб. Квадрат. Решение задач.

Ромб. Квадрат. Свойство ромба.

Ввести понятие ромба и квадрата как частных видов параллелограмма. Рассмотреть свойства и признаки ромба и квадрата и показать их применение в процессе решения задач. Совершенствовать навыки решения задач.

признаки и свойства // прямых, признаки равенства треугольников

Регулятивные УУД:

Владеть способами самоопределения в ситуациях выбора на основе собственных позиций

С.р.

Осевая и центральная симметрии. Решение задач.

Симметричные фигуры, симметрия относительно точки и прямой.

Рассмотреть осевую и центральную симметрию как свойства некоторых геометрических фигур. Научить строить симметричные точки и распознавать фигуры, обладающие осевой и центральной симметрией. Совершенствовать навыки решения задач.

Построение параллельных прямых, отрезка равного данному

Познавательные УУД: Задавать вопросы к наблюдаемым фактам, отыскивать причины явлений, обозначать своё понимание или непонимание по отношению к изучаемой проблеме

Пр.р.

презентация

Контрольная работа №1 по теме «Четырёхугольники».

Проверка знаний, умений применять эти знания и навыков, учащихся в процессе выполнения самостоятельной работы.

Регулятивные УУД:

Осуществлять индивидуальную образовательную траекторию с учетом общих требований и норм

Глава 6. Площадь фигур. (14 ч)

Основная цель: сформировать у учащихся понятие площади многоугольника, развивать умение вычислять площади фигур, применяя изученные свойства и формулы, применять теорему Пифагора, расширить и углубить представления учащихся об измерении площадей; формировать геометрическую культуру, логическое мышление, математическую речь.

Площадь многоугольника.

Понятие площадь, единицы измерения площадей, площадь многоугольника.

Дать представление об измерении площадей многоугольников. Ввести формулу для вычисления площади квадрата. Использование теоретического материала в ходе решения задач.

Старинные и современные единицы измерения площадей. Способы измерения и вычисления площадей фигур.

Регулятивные УУД:

Ставить цель и организовывать её достижение, уметь пояснить свою цель

Площадь квадрата, прямоугольника.

Ввести понятие площади прямоугольника и показать ее применение в процессе решения задач.

Старинные и современные единицы измерения площадей. Способы измерения и вычисления площадей фигур.

Регулятивные УУД:

Уметь принимать решения, брать на себя ответственность за их последствия

Площадь параллелограмма.

Площадь параллелограмма, высота параллелограмма, биссектриса угла параллелограмма.

Вывести формулу для вычисления площади параллелограмма и показать применение этой формулы в процессе решения задач.

признаки и свойства // прямых, свойства п/у Δ

Регулятивные УУД:

Ставить цель и организовывать её достижение, уметь пояснить свою цель

Площадь треугольника.

Формулы для вычисления площади треугольника

Вывести формулы для вычисления площади треугольника и показать их применение в процессе решения задач.

виды треугольников их свойства

Регулятивные УУД:

Организовывать планирование, анализ, рефлексию, самооценку своей учебно- познавательной деятельности

Теоретический тест

Площадь трапеции. Решение задач.

Площадь трапеции.

Рассмотреть теорему о площади трапеции и показать ее применение в процессе решения задач.

виды треугольников их свойства, признаки и свойства // прямых, свойства п/у Δ

Регулятивные УУД:

Ставить познавательные задачи и выдвигать гипотезы; выбирать условия проведения наблюдения или опыта; владеть измерительными навыками, работать с инструкциями

Ср.

Теорема Пифагора. Теорема, обратная теореме Пифагора. Решение задач.

Теорема Пифагора. Теорема, обратная теореме Пифагора.

Рассмотреть теорему Пифагора и теорему, обратную теореме Пифагора показать применение в ходе решения задач.

Прямоугольный треугольник, свойства. Квадрат числа. Формулы вычисления площадей всех изученных фигур.

Регулятивные УУД:

Ставить цель и организовывать её достижение, уметь пояснить свою цель

Практическая работа

Тестовая работа

Контрольная работа №2 по теме «Площадь».

Регулятивные УУД:

Осуществлять индивидуальную образовательную траекторию с учетом общих требований и норм

Глава 7. Подобные треугольники. (19 ч)

Основная цель: дать учащимся систематические сведения о четырехугольниках и их свойствах; сформировать представления о фигурах, симметричных относительно точки и прямой; совершенствовать навыки решения геометрических задач; формировать геометрическую культуру, логическое мышление, математическую речь.

Определение подобных треугольников. Отношение площадей подобных треугольников.

Понятие отношения отрезков и подобие треугольников.

Ввести понятие пропорциональных отрезков и подобных треугольников. Рассмотреть свойство биссектрисы треугольника и показать его применение в процессе решения задач.

Понятия: отношение, пропорциональность, пропорциональные отрезки, биссектриса, периметр.

Регулятивные УУД:

Уметь принимать решения, брать на себя ответственность за их последствия

Признаки подобия треугольников. Решение задач.

Признаки подобия треугольников.

Рассмотреть признаки подобия треугольников и сформировать навыки применения этого признака при решении задач.

Понятия: отношение, пропорциональность, пропорциональные отрезки, биссектриса, периметр.

Познавательные УУД: Ставить познавательные задачи и выдвигать гипотезы; выбирать условия проведения наблюдения или опыта; владеть измерительными навыками, работать с инструкциями

С.р.

презентация

Контрольная работа №3 по теме «Признаки подобия треугольников».

Проверка знаний, умений применять эти знания и навыков у учащихся в процессе выполнения самостоятельной работы.

Регулятивные УУД:

Осуществлять индивидуальную образовательную траекторию с учетом общих требований и норм

Средняя линия треугольника. Свойство медиан треугольника.

Рассмотреть теорему о средней линии треугольника и свойство медиан треугольника, показать их применение при решении задач.

Понятия: биссектриса, медиана, высота треугольника. признаки и свойства // прямых

Регулятивные УУД:

Владеть навыками работы с различными источниками информации

Тест.р

Пропорциональные отрезки.

Понятие среднего пропорционального (среднего геометрического) двух отрезков, пропорциональные отрезки в п/у Δ, свойство высоты п/у Δ.

Ввести понятие среднего пропорционального (среднего геометрического) двух отрезков. Сформировать навыки использования изученной теоремы в процессе решения задач.

признаки и свойства // прямых, прямоугольный треугольник,

теорема Пифагора

Регулятивные УУД:

Ставить цель и организовывать её достижение, уметь пояснить свою цель

Измерительные работы на местности. Задачи на построение методом подобия.

Показать применение подобия треугольников в измерительных работах на местности. Совершенствовать навыки решения задач на построение.

Регулятивные УУД:

Уметь принимать решения, брать на себя ответственность за их последствия

Практ.р.

Синус, косинус и тангенс острого угла прямоугольного треугольника. Соотношения между сторонами и углами прямоугольного треугольника. Решение задач.

Синус, косинус и тангенс острого угла прямоугольного треугольника. Соотношения между сторонами и углами прямоугольного треугольника.

Ввести понятие синуса, косинуса и тангенса острого угла п/у Δ. Ознакомить с основным тригонометрическим тождеством и показать его применение в процессе решения задач.

Прямоугольный треугольник, биссектриса, пропорциональные отрезки, признаки подобия

Регулятивные УУД:

Самостоятельно искать, извлекать, систематизировать, анализировать и отбирать необходимую для решения учебных задач информацию

Теоретический тест

презентация

Контрольная работа №4 по теме «Соотношения между сторонами и углами прямоугольного треугольника».

Регулятивные УУД:

Осуществлять индивидуальную образовательную траекторию с учетом общих требований и норм

Глава 8. Окружность. (16 ч)

Основная цель: дать учащимся систематизированные сведения об окружности и ее свойствах, вписанной и описанной окружностях; совершенствовать навыки решения геометрических задач; формировать геометрическую культуру, логическое мышление, математическую речь.

Взаимное расположение прямой и окружности.

Рассмотреть различные случаи взаимного расположения прямой и окружности. Совершенствовать навыки решения задач.

Теорема Пифагора, квадрат числа, квадратный корень, понятия: окружность, радиус, диаметр, хорда.

Регулятивные УУД:

Владеть способами самоопределения в ситуациях выбора на основе собственных позиций

презентация

Касательная к окружности. Решение задач.

Окружность. Касательная к окружности.

Ввести понятие касательной, точки касания, отрезков касательных, проведенных из одной точки и показать их применение при решении задач. Свойство отрезков касательных, проведенных из одной точки и показать его применение в процессе решения задач.

Теорема Пифагора, квадрат числа, квадратный корень, понятия: окружность, радиус, диаметр, хорда.

Регулятивные УУД:

Задавать вопросы к наблюдаемым фактам; отыскивать причины явлений, обозначать своё понимание или непонимание к изучаемой проблеме

С.р.

Центральный и вписанный углы. Теорема об отрезках пересекающихся хорд. Решение задач по теме «Центральный и вписанные углы».

Градусная мера дуги. Центральный и вписанный углы. Теорема об отрезках пересекающихся хорд.

Ввести понятие градусной меры дуги окружности, центрального, вписанного углов, показать применение знаний при решении задач. Рассмотреть теорему об отрезках пересекающихся хорд и показать ее применение при решении задач.

Теорема Пифагора, квадрат числа, квадратный корень, понятия: окружность, радиус, диаметр, хорда

Регулятивные УУД:

Организовывать планирование, анализ, рефлексию, самооценку своей учебно- познавательной деятельности

С.р.

Замечательные точки треугольника. Свойство биссектрисы угла и серединного перпендикуляра к отрезку.

Свойство биссектрисы угла и серединного перпендикуляра к отрезку.

Рассмотреть свойство биссектрисы угла, понятие серединного перпендикуляра и показать применение при решении задач.

понятия: окружность, радиус, диаметр, хорда, биссектриса, серединный перпендикуляр.

Регулятивные УУД:

Замечательные точки треугольника. Теорема о точке пересечения высот треугольника.

Теорема о точке пересечения высот треугольника.

Рассмотреть теорему о точке пересечения высот треугольника и показать ее применение при решении задач.

Биссектриса, медиана, высота треугольника.

Регулятивные УУД:

Вписанная и описанная окружности. Свойство описанного и вписанного четырехугольника. Решение задач.

Вписанная и описанная окружности. Свойство описанного и вписанного четырехугольник

Ввести понятия вписанной и описанной окружностей, свойство четырехугольника. Рассмотреть теоремы и их применение при решении задач.

Биссектриса, медиана, высота треугольника. Свойство биссектрисы угла и серединного ┴ к отрезку.

Регулятивные УУД:

Уметь принимать решения, брать на себя ответственность за их последствия

С.р.

Контрольная работа №5 по теме «Окружность».

Регулятивные УУД:

Осуществлять индивидуальную образовательную траекторию с учетом общих требований и норм

Повторение по темам «Четырехугольники», «Площадь».

Повторение основных понятий по темам, совершенствовать навыки решения задач.

Регулятивные УУД:

Владение навыками контроля и оценки своей деятельности. Преодоление трудностей.

Тест

Повторение по темам «Подобные треугольники», «Окружность».

Систематизировать теоретические знания по темам, совершенствовать навыки решения

Регулятивные УУД:

Владение навыками контроля и оценки своей деятельности. Преодоление трудностей.

Тест

⇧

⇩

скачать материал