Книга-пособие для учащихся 5-6 классов по математике

яблоки. Сколько килограммов груш, винограда и яблок привезли в магазин?

Решение:

I способ:

1) 250 : 100 5 = 12,5 (кг) - груш.

2) 250 : 100 25 = 62,5 (кг) - винограда.

3) 12,5 + 62,5 = 75 (кг) груш и винограда вместе.

4) 250 - 75 = 175 (кг) - яблок.

II способ:

1) 5% = 0,05

2)25% = 0,25.

3) 250 0,05 = 12,5 (кг) - груш

4) 250 0,25 = 62,5 (кг) - винограда

5) 12,5 + 62,5 = 75 (кг) груш и винограда вместе.

6) 250 - 75 = 175 (кг) - яблок.

Задача: Из 800 учащихся школы 60% принимало участие в кроссе. Сколько учащихся этой школы не участвовало в кроссе?

I способ:

1) 800 : 100 60 = 480 (уч) - участвовали

2) 800 - 480 = 320 (уч) - не участвовали.

II способ:

1) 100% - 60% = 40%

2) 800 : 100 40 = 320 (уч) - не участвовали.

-19-

Действия с десятичными дробями.

1) Сложение и вычитание десятичных дробей

При сложении или вычитании десятичных дробей запятую пишут под запятой и уравнивают количество цифр после запятой.

:

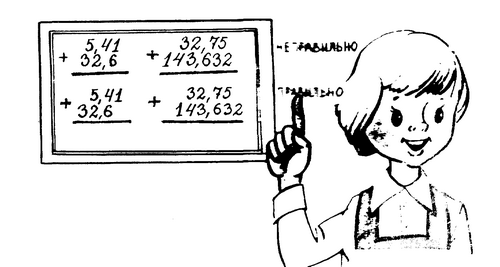
Например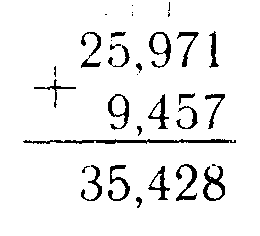

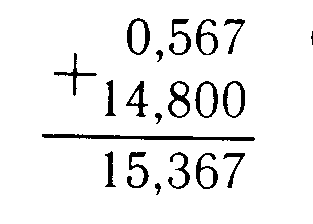
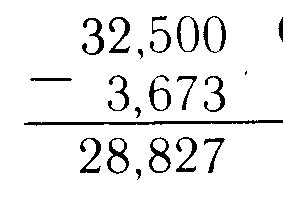
2) Умножение десятичных дробей.

Умножают десятичные дроби как простые числа, затем считают количество цифр после запятой, и в произведении столько цифр отделяют запятой.

Например:

-1-

Проценты.

Определение: Процентом называют сотую часть числа. Всё число - 100%.

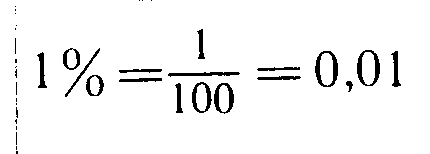
1) Чтобы найти 1% от любого числа нужно просто разделить это число на 100.

Например: а) Найти 1% от 25.

Решение: 25 : 100 = 0,25;

б) Найти 1% от 1200;

Решение: 1200 : 100 = 12;

в) Найти 1% от 0,5;

Решение: 0,5 : 100 = 0,005;

г) Найти 1% от ;

Решение: : 100 = = ;

д) Найти 1% от 3;

Решение: 3 : 100 = ;

2) Если требуется найти большее число процентов, то нужно разделить на 100, а затем умножить на количество процентов.

-17-

4) Деление десятичных дробей.

При делении десятичных дробей вначале переносят запятую вправо в делителе и делимом на столько цифр, сколько цифр после запятой в делителе. Затем делят целую часть, после переносят запятую в частное и продолжают деление.

Например:

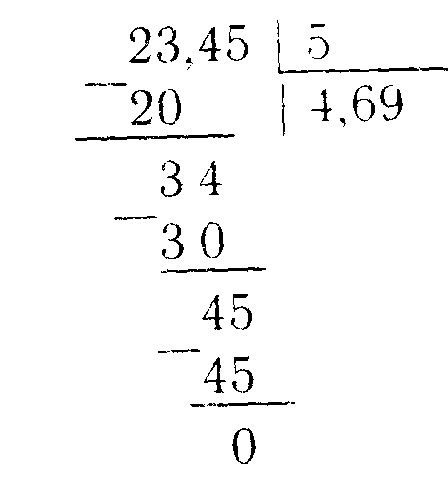
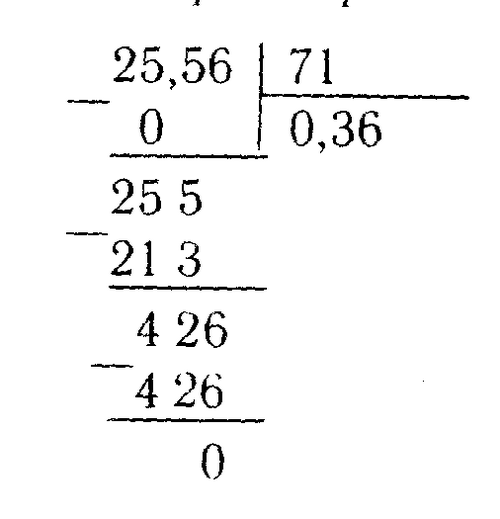
-3-

3) Умножение обыкновенных дробей.

При умножении десятичных дробей числитель умножают на числитель, а знаменатель умножают на знаменатель.

(Если в числителе и знаменателе есть числа, которые можно сократить, то в начале нужно сократить, а только потом выполнять умножение. Так пример будет решаться проще).

Например: а) = = = ;

б) = = = ;

Если умножаются смешанные числа, то их вначале нужно перевести в обыкновенные дроби, а потом выполнить умножение.

Например: а) 5 1 = = = 7;

б) 24 = = = = 10;

в) 315 = = = = 55;

4) Деление обыкновенных дробей.

При делении обыкновенных дробей первую дробь переписывают, затем деление заменяют умножением и вторую дробь переворачивают. Далее выполняют

-7-

Действия с обыкновенными

дробями.

1) Сложение и вычитание обыкновенных дробей.

При сложении и вычитании обыкновенных дробей вначале находят общий знаменатель (это число, которое делится на все знаменатели дробей). Затем находят дополнительные множители (это числа, которые получаются при делении общего знаменателя на знаменатели дробей). Далее умножают дополнительные множители на числители и выполняют сложение их или вычитание.

Полученные дроби нужно обязательно сократить (если получилась сократимая дробь) или выделить целую часть (если это возможно).

Например:

а) = = = 1;

б) - = = ;

в) + - = = = ;

-5-

Например: а) Даны числа: 2; 3,5; 5,2; 9,1 и 10. Найти медиану.

Все числа записаны в порядке возрастания и их нечетное количество, поэтому медиана = 5,2;

б) Даны числа: 5; 8; 8; 17; 19 и 25. Найти медиану.

Все числа записаны в порядке возрастания и их четное количество, поэтому (8 + 17) : 2 = 12,5;

-15-

в) 1,5 (3,2 - 0,4) = 1,5 3,2 - 1,5 0,4 = 4,8 - 0,6 = 4,2;

г) 28х (5 + х) = 140х + 28х²;

д) 5ав - 15а = 5а (в - 3);

е) 8х⁵у³ + 2х²у = 2х²у (4х³у² + 1);

4) Умножение на нуль и единицу.

а) При умножении числа на нуль в ответе получается нуль.

Например: 28 0 = 0; 0 (-28) = 0;

0 28 = 0; -28 0 = 0;

б) При умножении числа на единицу получается тоже число.

Например: 28 1 = 28; 1 (-28) = -28;

1 28 = 28; -28 1 = -28;

-13-

4) Свойство вычитания суммы из числа.

Чтобы вычесть сумму из числа, можно из него вычесть одно слагаемое и затем из результата вычесть другое слагаемое.

а - (в + с) = (а - в) - с или а - (в + с) = (а - с) - в;

Например: 29 - (5 + 7) = 29 - 5 - 7 = 17;

0,5 - (0,3 + 28,17) = 0,5 - 0,3 -28,17 = - 27,97;

5) Свойство вычитания числа из суммы.

Чтобы вычесть число из суммы, можно вычесть его из одного слагаемого и к результату прибавить другое слагаемое.

(а + в) - с = (а - в) + с; или (а + в) - с = (а - с) + в;

Например: (14 + 10) - 5 = (10 - 5) + 14 = 19;

(25,5 - 0,15) - 0,5 = (25,5 - 0,5) - 0,15 = 24,85;

-11-

Действия с положительными и

отрицательными числами.

1) Сложение чисел с одинаковыми знаками.

Если знаки одинаковые, то модули складывают, а знак оставляют.

Например: а) 26 + 10 = 36; б) -2,5 -25 = -27,5;

в) -28 - 0,23 = --28,23; г) -1,15 -0,25 = - 1,4;

2) Сложение чисел с разными знаками.

Если знаки разные, то от большего модуля отнимают меньший модуль и ставят знак большего модуля.

Например: а) 26 + (- 6) = 20; б) 0,3 + (- 1,2) = - 0,9;

в) - 17 + 30 = 13; г) 80 - 120 = - 40;

3) Умножение и деление положительных и отрицательных чисел.

а) Плюс умножить или разделить на минус получится минус.

б) Минус умножить или разделить на плюс получится минус.

в) Минус умножить или разделить на минус получится плюс.

Например: 25 (-8) = -200; 100 : (-25) = -4;

-25 8 = -200; -100 : 25 = -4;

-25 (-8) = 200; -100 : (-25) = -4;

-9-

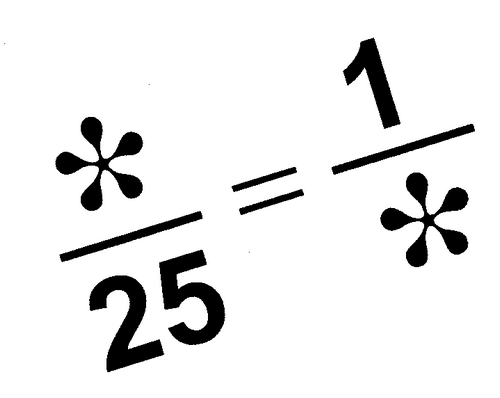
Автор: Тятюшкина А.А. учитель математики

МОУ «СОШ №11».

Компьютерная верстка автора.

Данный справочник имеет двойное назначение.

Во - первых, здесь можно навести моментальную справку по

основным разделам математики 5 - 6 классов. Во - вторых,

он может служить общедоступным пособием для повторения элементарной математики при подготовке

к ГИА и ЕГЭ.

По данному справочнику можно учиться. В нем доступным языком изложены основные правила курса математики 5 - 6 классов. Это действия с десятичными и обыкновенными дробями, действия с положительными и отрицательными числами. Дано понятие процента, а также разобраны примеры к каждому правилу.

Простейшие уравнения.

Определение: Уравнением называют равенство с переменной.

Решить уравнение - значит найти его корни. Корнем уравнения называют число при подстановке которых в уравнение получается верное равенство. Если равенство получается не верное, то уравнение решено не верно.

Решение простейших уравнений.

I способ:

Чтобы решать простейшие уравнения, нужно знать некоторые правила.

Правила:

1) Чтобы найти неизвестное слагаемое, нужно от суммы вычесть другое слагаемое.

Если х + а = в, то х = в - а;

2) Чтобы найти неизвестное уменьшаемое, нужно к разности прибавить вычитаемое.

Если х - а = в, то х = в + а;

3) Чтобы найти неизвестное вычитаемое, нужно от уменьшаемого вычесть разность.

Если а - х = в, то х = а - в;

4) Чтобы найти неизвестный множитель, нужно произведение разделить на другой множитель.

Если а х = в, то х = в : а;

5) Чтобы найти неизвестное делимое, нужно частное умножить на делитель.

Если х : а = в, то х = в а;

-1-

Примеры:

3 - 1 = 2

1) а - 45 = 300, так как 3 = 2 + 1, то

а = 300 + 45

а = 345.

3 - 1 = 2

2) 3,7 - х = -2,3, так как 1 = 3 - 2,то

х = 3,7 - (-2,3)

х = 6.

6 : 2 = 3

3) 36 : у = 9 , так как 2 = 6 : 3, то

у = 36 : 9

у = 4.

3 - 2 = 1

4) 4,8 - в = 5, 6, так как 2 = 3 - 1,

в = 4,8 - 5,6

в = - 0,8.

6 : 2 = 3

5) х : 15,2 = - 1,05, так как 6 = 3 2, то

х = - 1,05 15,2

х = - 15,96.

6 : 2 = 3

6) - : у = - 0,5, так как 2 = 6 : 3, то

у = - : (- 0,5)

у = ;

-3-

4) - 2 (х - 4,3) + 2,7 = 3х + 3,1; раскроем скобки

- 2х + 8,6 + 2,7 = 3х + 3,1; перенесем с буквой в одну сторону, а без буквы в другую

- 2х - 3х = 3,1 - 8,6 - 2,7; приведем подобные слагаемые

- 5х = - 8,2

х = - 8,2 : (- 5)

х = 1,64.

5) (х - )15 = 8; раскроем скобки

х 15 - 15 = 8; умножаем

10х - 12 = 8

10х = 8 + 12

10х = 20

х = 2;

Решение линейных уравнений.

1) (2,8 - х) : 0,3 = 0,7; неизвестное находится в скобках,

поэтому находим значение скобок

2,8 - х = 0,70,3

2,8 - х = 0,21

- х = 0,21 - 2,8

- х = - 2,59; меняем знаки в обеих частях, т.е. умножаем на

х = 2,59 - 1.

2) 0,39 : х - 0,1 = 0,16; неизвестное связано с 0,39, поэтому

0,39 : х = 0,16 + 0,1

0,39 : х = 0,26;

х = 0,39 : 0,26; х = 1,5;

-5-

3) (х - 1) (х + 4) = 0;применяем свойство,

здесь переменная находится в обеих скобках, значит

х - 1 = 0 или х + 4 = 0, т.е придется решить 2 уравнения

х = 1 х = - 4

Ответ: х₁ = 1; х₂ = - 4;

Содержание.

1) Действия с десятичными дробями

Сложение и вычитание десятичных дробей 1

Умножение десятичных дробей. 1

Умножение и деление десятичных дробей на 10,

100, 1000 и т.д. 2

Деление десятичных дробей. 3

Округление десятичных дробей 4

Перевод десятичных дробей в обыкновенные. 4

2) Действия с обыкновенными дробями.

Сложение и вычитание обыкновенных дробей 5

Сложение и вычитание смешанных чисел 6

Умножение обыкновенных дробей 7

Деление обыкновенных дробей. 7

Перевод обыкновенных дробей в десятичные. 8

3) Действия с положительными и

отрицательными числами.

Сложение чисел с одинаковыми знаками. 9

Сложение чисел с разными знаками. 9

Умножение и деление положительных и отрицательных чисел. 9

5) Свойства действий с числами.

Свойства (законы) сложения 10

Свойства (законы) умножения. 12

6) Среднее арифметическое, мода,

размах и медиана. 14

7)Нахождение дроби от числа и числа 16

по его дроби.

8) Проценты 17

9) Формулы 20

Например: а) Найти 3% от 25.

Решение: 25 : 100 3 = 0,75;

б) Найти 15% от 1200;

Решение: 1200 : 100 15 = 180;

в) Найти 10% от 0,5;

Решение: 0,5 : 100 10 = 0,05;

3) Очень часто в задачах требуется найти число по количеству его процентов. Для этого нужно число разделить на количество процентов, а потом умножить на 100.

Например: а) Найти число, если 5% его составляют 25.

Решение: 25 : 5 100 = 500;

б) 120% числа равны 12. Найти число.

Решение: 12 : 120 100 = 10;

в) Найти число, если 15% его равны 3,9.

Решение: 3,9 : 15 100 = 26;

4) Работать с процентами можно проще, если перевести проценты в дробь. Но тогда нужно хорошо уметь находить дробь от числа и число по его дроби.

5% = 0,05;

10% = 0,1;

120% = 1,2;

0,23% = 0,0023;

Задача: В магазин привезли 250 кг фруктов. 5% всех фруктов составляют груши, 25% - виноград, а остальное-

-18-

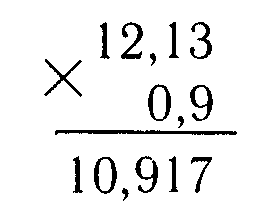
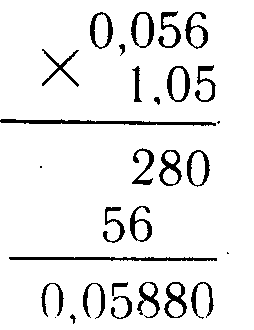
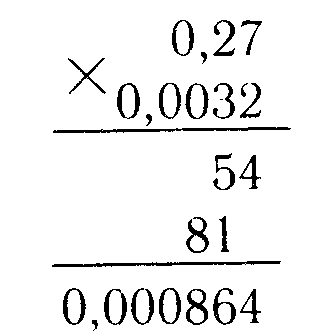
3) Умножение и деление десятичных дробей на 10, 100, 1000 и т.д.

а) Умножение на 10, 100, 1000 и т. д.

При умножении на 10, 100, 100 и т. д. передвигают запятую в десятичной дроби вправо на столько цифр, сколько нулей в числе.

Например: 2,25 10 = 22,5; 23,05 1000 = 23050;

0,037 1000 = 37; 0,5 1000 = 500;

б) Деление на 10, 100, 1000 и т. д.

При делении десятичной дроби на 10, 100, 1000 и т. д. переносят запятую влево на столько цифр, сколько нулей в числе.

Например: 2,25 : 10 = 0,225; 23,05 : 1000 = 0,02305;

0,5 : 100 = 0,005; 0,037 : 1000 = 0,000037;

-2-

Нахождение дроби от числа и

числа по его дроби.

1) Нахождение дроби от числа.

Чтобы найти дробь от числа надо это число умножить на дробь.

Например: а) Найти от 15.

Решение: 15 = = 10;

б) Найти 0,15 от 1,5;

Решение:1,5 0,15 = 0,225;

в) Найти 2,5 от .

Решение: 2,5 = = = 1;

2) Нахождение числа по его дроби.

Чтобы найти число по его дроби, надо число разделить на дробь.

Например: а) Найти число, если его равны 10;

Решение: 10 : = = 15;

б) Найти число, если 0,4 его равны ;

Решение: : 0,4 = : = = = 1 = 1;

-16-

II Законы умножения (свойства).

1) Переместительный закон.

От перемены мест множителей произведение не меняется.

Например: 5 28 = 28 5 = 140;

(Всегда проще большое число умножать на маленькое).

2) Сочетательный закон.

Нет разницы, как выполняется умножение. Всегда вначале умножают те числа, которые при умножении дают нуль в конце числа.

Например:

а) 25 12 4 = 25 4 12 = 100 12 = 1200;

б) 0,15 0,25 0,6 = 0,15 0,6 0,25 = 0,09 0,25 = 0,0225;

3) Распределительный закон.

а в а с = а (в с); или

а (в с) = а в а с;

Число стоящее за скобками нужно умножить на каждое число, стоящее в скобках. Или наоборот, общий множитель нужно вынести за скобки, а в скобках оставить оставшиеся множители.

( Его применяют при раскрытии скобок или тогда, когда нужно вынести общий множитель за скобки).

Например:

а) 28 56 + 44 28 = 28 (56 + 44 ) = 28 100 = 2800;

б) 1,5 3,2 - 1,5 0,4 = 1,5 (3,2 - 0,4) = 1,5 2,8 = 4,2;

-12-

Среднее арифметическое, мода,

размах и медиана.

I. Среднее арифметическое нескольких чисел.

Чтобы найти среднее арифметическое нескольких чисел, нужно все эти числа сложить, а затем поделить на количество чисел.

Например: Даны числа 5; 1,5; 8,3; 2,5. Найти среднее арифметическое этих чисел.

(5 + 1,5 + 8,3 + 2,5) : 4 = 4,325;

II. Мода.

Модой называют число, которое повторяется чаще других.

Например: Даны числа: 5; 8; 8; 17; 19 и 25. Найти моду.

Чаще других повторяется число - 8, значит мода = 8;

Если разные числа повторяются одинаковое число раз, то моды нет.

III. Размах.

Размахом называют разность между самым большим числом и самым маленьким.

Например: Даны числа: 5; 8; 8; 17; 19 и 25. Найти размах.

25 - 5 = 20; Размах = 20;

IV. Медиана.

Медианой называют число, которое стоит в середине ряда, записанного в порядке возрастания. Если чисел четное количество, то берут два средних числа и находят среднее арифметическое этих чисел.

-14-

5) Округление десятичных дробей.

При округлении десятичной дроби до разряда единиц, десятых, сотых и т. д. поступают следующим образом:

1) отбрасывают все цифры, стоящие за этим разрядом справа.

2) последнюю из оставшихся цифр не меняют, если первая из отбрасываемых цифр 0, 1, 2, 3 или 4, и последнюю из оставшихся цифр увеличивают на 1, если первая из отбрасываемых цифр 5, 6, 7, 8 или 9.

Например:

а) 31,967 = 31,97 (округлили до сотых)

б) 15,6782 = 15,678 (округлили до тысячных)

в) 0,653 = 0,7 (округлили до десятых)

г) 12,32 = 12 (округлили до целых)

д) 12,567 = 10 (округлили до десятков)

6) Перевод десятичных дробей в обыкновенные.

Например: а) 0,6 = = ; б) 1,25 = 1 = 1;

в)25,375 = 25 = 25 = 25;

-4-

2) Сложение и вычитание смешанных чисел

При сложении и вычитании смешанных чисел вначале складывают или вычитают целые части, а потом выполняют действия с дробями (смотри правило - пункт 1).

Например:

а) 16 + 19 = 35 = 35;

б) 5 + 3 = 8 = 8 = 9;

в) 5 -- 2 = 3 = 3;

г) 3-- 1= 2 = 1 = 1;

Когда занимаем единицу, то она превращается в дробь знаменатель которой равен общему знаменателю дробей, то есть 1 = = = и так далее.

Например:

1 -- = = ;

5 -- = 4 = 4;

-6-

умножение обыкновенных дробей.

Например: а) : = = = ;

б) 3 : 1 = : = = = = 2;

в) 8 : = = = 12;

г) 3 : 14 = : = = ;

5) Перевод обыкновенных дробей в десятичные.

Например: а) 3 = 3,5; б) 3 = 3,5;

в) 5 = 5,375;

Просто надо вспомнить, что дробная черта - это знак деления, и выполнить деление числителя на знаменатель.

-8-

Свойства действий с числами.

I) Свойства (законы) сложения.

1) Переместительный закон.

От перемены мест слагаемых сумма не меняется.

Например: 28 + 126 = 126 + 28 = 154;

(Всегда проще к большому числу прибавить маленькое число)

2) Сочетательный закон.

Нет разницы, как выполняется сложение. Всегда вначале складывают те числа, которые при сложении дают нуль в конце числа.

Например:

а) 28 + 256 + 172 = (28 + 172) + 256 = 200 + 256 = 456;

б) 28,56 + 1,55 + 1,45 = (1,55 + 1,45) + 28,56 = 3 + 28,56 =

= 31,56;

в) 25,12 + 0,3 + 0,88 + 5,7 = (25,12 + 0,88) + (0,3 + 5,7) =

= 26 + 6 = 32;

г) -5,125 + 8,6 - 2,375 + 2,3 = (-5,125 - 2,375) + (8,6 + 2,3) =

= - 7,5 + 10,9 = 3,4;

3) Закон поглощения нуля.

Если к нулю прибавить какое-то число, то число не изменится. Если к числу прибавить нуль, то число тоже не изменится.

Например: а) 28 + 0 = 28; б) 0 + 2,5 = 2,5;

в) -0,56 -0 = -0,56; г) 0 - 100 = -100;

-10-

Справочник

по математике

ПОСОБИЕ ДЛЯ УЧАЩИХСЯ

Формулы.

1) Площадь прямоугольника.

S = а в;

2) Периметр прямоугольника.

Р = (а + в) 2;

3) Объем прямоугольного параллелепипеда.

V = а в с;

4) Площадь круга.

S = П R²$

5) Длина окружности.

С = 2ПR;

6) Чтобы найти неизвестный делитель, нужно делимое

разделить на частное.

Если а : х = в, то х = а : в;

Примеры:

а) х + 467 = 1500; применяем правило №1

х = 1500 - 467;

х = 1033;

б) 510 - а = 147; применяем правило № 3

а = 510 - 147

а = 363;

в) у - 869 = 329; применяем правило № 2

у = 329 + 869

у = 1198;

г) 47х = 611; применяем правило № 4

х = 611 : 47

х = 13;

д) 1521 : м = 9, применяем правило № 6

м = 1521 : 9

м = 169;

е) п : 77 = 14, применяем правило № 5

п = 14 77

п = 1078;

II способ:

Очень часто многие учащиеся забывают данные правила, особенно тогда, когда в уравнениях есть не только положительные числа, но и отрицательные. Поэтому существует другой способ, который большинству учащихся нравится больше. Нужно просто сверху над элементами уравнения записать карандашом простейший пример. Находим в записанном примере, то число, которое записано над переменной и далее решаем уравнение.

-2-

Решение простейших линейных уравнений.

Порядок решения:

1) Раскрыть скобки, если они есть.

2) Привести подобные слагаемые.

3) Если переменные и свободные члены есть в обеих

частях уравнения, то нужно перенести с буквой в одну сторону, а без буквы в другую.

4 Далее решать, используя I способ или II способ.

Примеры:

1) 7(х + 6) = 49; раскроем скобки

5 + 2 = 7

7х + 42 = 49, так как 5 = 7 -2, то

7х = 49 - 42

23 = 6

7х = 7, так как 3 = 6 : 2, то

х = 7 : 7

х = 1.

2) 12 (х + 9х) = 1200, приведем подобные слагаемые

12 10х = 1200, перемножаем

120 х = 1200

х = 1200 : 120

х = 10.

3) 7 (2х - 3) + 4 (3х - 2) = - 3, раскроем скобки

14х - 21 + 12х - 8 = - 3, приведем подобные слагаемые

26х - 29 = - 3 перенесем - 29 в правую сторону

26х = - 3 + 29

26х = 26

х = 26 : 26 = 1.

-4-

Решение линейных уравнений,

записанных в виде пропорции.

Определение: Равенство двух отношений называют пропорцией.

Основное свойство пропорции: Произведение крайних членов равно произведению средних членов.

1) = ; применяем свойство пропорции

48х = 240;

х = 240 : 48; х = 5;

2) 3 : к = 1 : 2; применяем свойство пропорции

1к = 32;

1к = 6;

к = 6 : 1; к = 2;

3) 4 : (2х) = 1,3 : 3; применяем свойство пропорции

2х 1,3 = 43; перемножаем

2,6х = 13;

х = 13 : 2,6; х = 5;

4) 2 : 0,24 = 1 : (х + 0,06); применяем свойство пропорции

2 (х + 0,06) = 0,24 1; перемножаем

-6-

2х + 20,06 = ;

2х + = ;

2х = - ;

2х = ;

х = ; 2; х = 0,1;

5) = ; применяем свойство пропорции

(х + 7) 5 = 3 (2х - 3); раскроем скобки

5х + 35 = 6х - 9; с буквой в одну сторону, а без буквы в

5х - 6х = -9 - 35; другую. - 1х = - 44; меняем знаки, т.е. делим на - 1.

х = 44;

Решение уравнений, применяя свойство

умножения числа на нуль.

Вы знаете, что если нуль умножить на какое-нибудь число, то получится нуль, т. е. а 0 = 0 и 0 а = 0;

1) 4 (х - 5) = 0; применяем свойство

т. к. 4 0, то х - 5 = 0; решаем маленькое уравнение

х = 5;

2) (3х + 6) 2,4 = 0; применяем свойство, т. к.

2,4 0, то 3х + 6 = 0; значит

3х = - 6; х = - 2;

-7-