Урок по теме 'Решение задач с помощью дробно - рациональных уравнений'

Конспект урока по алгебре в 8 классе по теме

«Решение задач с помощью дробно - рациональных уравнений»

Цель: Совершенствовать навык составления уравнения по условию задачи, умения проверять соответствие найденного решения условию задачи. Сформировать умение применять дробно-рациональные уравнения при решении задач.

Задачи:

1) Дидактические:

- повторить понятия: корень уравнения, дробно-рациональное уравнение;

- совершенствовать умения учащихся применять алгоритм решения дробно-рациональных уравнений;

2) Развивающие:

- совершенствование вычислительных навыков учащихся;

- развитие устной и письменной речи;

- развитие основных мыслительных операций (анализ, синтез, сравнение, обобщение);

3) Воспитательные:

- развитие внимания и аккуратности;

- развитие элементов творческой деятельности, как качеств мышления.

Тип урока: урок совершенствования знаний, умений и навыков.

Форма работы: фронтальная, индивидуальная.

Методы: репродуктивный, продуктивный, творческий.

Учебник: Алгебра: Учебник для 8 класса общеобразовательных учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под ред. С. А. Теляковского. - М.: Просвещение, 2011 г.;

Ход урока

I. Проверка домашнего задания (фронтально)

II. Устная работа

1. Какие уравнения являются дробно-рациональными?

2. Что такое корень уравнения?

3. Что значит решить уравнение?

4. Когда дробь равна нулю?

5. Когда равны две дроби с одинаковыми знаменателями?

6. Сформулировать алгоритм решения дробно-рациональных уравнений.

7. Проверить, являются ли числа 1, 2, 4, 0, 3 корнями уравнений

.

8. Верно ли найдена ОДЗ уравнений:

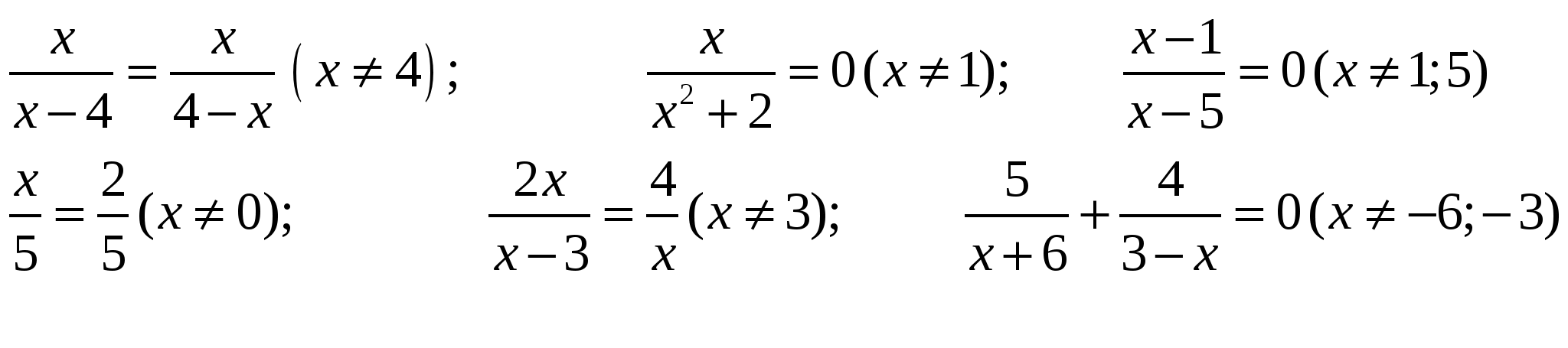
III. Домашнее задание: п. 26, № 620, 621.

IV. Объяснение нового материала.

Тема: Решение задач с помощью дробно-рациональных уравнений

Задача (на движение) № 618

Ответить на вопросы по тексту задачи:

1) Какой процесс описывается в задаче? (движение)

2) Какими величинами характеризуется этот процесс? (скорость, время, расстояние)

3) Как связаны между собой эти величины? ()

4) Сколько реальных процессов описывается в задаче? (2)

5) Значения каких величин известны? ()

6) Значения каких величин сравниваются ( на 20 км/ч, следовательно, на 1 час)

7) Значения каких величин требуется найти? (скорость каждого автомобиля)

Одну из неизвестных величин обозначить за х. Выразить неизвестные величины через х и известные величины. Используя одно из сравнений величин составить уравнение.

Пусть х км/ч - скорость второго автомобиля.

Тогда км/ч - скорость первого автомобиля;

ч - время движения второго автомобиля;

ч - время движения первого автомобиля.

По условию задачи, время движения первого автомобиля меньше времени движения второго автомобиля на 1 час. Составим уравнение:

.

Как еще можно составить уравнение? .

Ученик у доски решает уравнение (с комментарием). Ответ: скорость первого автомобиля 60 км/ч; скорость второго автомобиля 40 км/ч.

Задача № 619 (самостоятельно составляют уравнение, затем ученик записывает его на доске и решает)

.

Ответ: 12 км/ч скорость первого лыжника; 10 км/ч скорость второго лыжника.

Задача № 617 (решают самостоятельно с последующим разбором)

.

Ответ: заданная дробь.