- Учителю
- Урок в 8 классе на тему 'Преобразование выражений, содержащих арифметические корни'
Урок в 8 классе на тему 'Преобразование выражений, содержащих арифметические корни'






Преобразование выражений, содержащих арифметические квадратные корни
Цели:
-
повторить определение арифметического квадратного корня, свойства арифметического квадратного корня;
-
закрепить навыки и умения решения примеров на тождественные преобразования выражений, содержащих арифметические квадратные корни;
-
обобщить и систематизировать знания учащихся по этой теме;
-
воспитывать навыки самоконтроля и взаимоконтроля, интерес к предмету.
Оборудование: мультимедийный проектор, оценочные листы, карточки с тестом, карточки с домашним заданием.
Ход урока.
I. Организационный момент
- Сегодня на уроке мы будем повторять правила преобразования выражений, содержащих квадратные корни, преобразование корней из произведения, дроби и степени, умножение и деление корней, вынесение множителя за знак корня, внесение множителя под знак корня, приведение подобных слагаемых и освобождение от иррациональности в знаменателе дроби. Подвести итоги сегодняшнего урока поможет оценочный лист. Подпишите свои листы и ответьте на первый вопрос «Настроение в начале урока», выбрав один из смайликов.
II. Сообщение темы урока
Тема нашего урока «Преобразование выражений, содержащих арифметические квадратные корни». (Слайд №1)
В математике есть нечто,
вызывающее человеческий восторг.
Ф. Хаусдорф (Слайд №2)
III. Устная работа
1) Фронтальный опрос. (Слайд №3)
-
Дайте определение арифметического квадратного корня. (Арифметическим квадратным корнем из числа а называется неотрицательное число, квадрат которого равен а).
-
Перечислите свойства арифметического квадратного корня. (Арифметический квадратный корень из произведения неотрицательных множителей равен произведению корней из этих множителей. Арифметический квадратный корень из дроби, числитель которой неотрицателен, а знаменатель положителен, равен корню из числителя, делённому на корень из знаменателя).
-
Чему равно значение арифметического квадратного корня из х2? (|х|).
-
Чему равно значение арифметического квадратного корня из х2, если х≥0? х<0? (х. -х).
2) Устный счёт (Слайд №4)
Ну-ка в сторону карандаши!
Ни костяшек. Ни ручек. Ни мела.
"Устный счёт!" Мы творим это дело
Только силой ума и души.
Цифры сходятся где-то во тьме,
И глаза начинают светиться,
И кругом только умные лица.
Потому что считаем в уме!
 (Слайд №5-9)
(Слайд №5-9)
1. Вынесите множитель из-под знака корня:

 2. Внесите множитель под знак корня:
2. Внесите множитель под знак корня:
 3. Возведите в квадрат:
3. Возведите в квадрат:
4. Приведите подобные слагаемые:
IV. Работа по теме урока
1) Индивидуальная работа (Слайд №10)
На «божьей коровке» есть красные, желтые и зеленые пятнышки. Зеленые соответствуют заданиям базового уровня, желтые - заданиям повышенного уровня, красные - заданиям высокого уровня. Учащиеся выбирают задание на свое усмотрение. Трое учащихся, получив задание, решают его в тетрадях. (Слайд №11-13)
2) Работа с доской.
Остальные обучающиеся решают следующие задания:
1. Упростите выражение:  ; б)
; б) 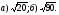
в) 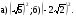 ; г)
; г) 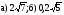
2. Выполните действия и соотнесите с верным ответом: 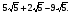 ,
, 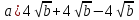 ,
, 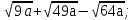 ,
, 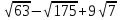 .
.
Ответы: -1; 6 - ;
; 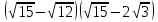 .
.
3. Освободитесь от иррациональности в знаменателе дроби.
а) 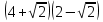 ; б)
; б)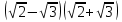 в)
в)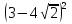 ; г)
; г) 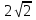 .
.
4. Сократите дробь.
а)  ; б)
; б)  ; в)
; в)  г)
г)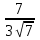
VI. Историческая справка (Слайд 14-16)
Radix- имеет два значения: сторона и корень. Греческие математики вместо «извлечь корень» говорили «найти сторону квадрата по его данной величине (площади)»
Начиная с XIII века, итальянские и другие европейские математики обозначали корень латинским словом Radix или сокращенно R (отсюда произошёл термин «радикал»).
Немецкие математики XV в. для обозначения квадратного корня пользовались точкой ·5
Позднее вместо точки стали ставить ромбик ¨5
 ¾
¾
Затем Ú 5 . Затем знак Ú и черту стали соединять.
VII. Тест (Слайд №17, 18)
Английский философ Герберт Спенсер говорил: «Дороги не те знания, которые откладываются в мозгу, как жир, дороги те, которые превращаются в умственные мышцы».
На этом этапе урока необходимо применить свои знания к решению упражнений в ходе выполнения теста.
VI. Взаимопроверка (Слайд №19)
Код правильных ответов: I вариант - 12312, II вариант - 32132.
VIII. Физкультминутка для глаз (Слайд №20, 21)
VII. Домашнее задание. (Слайд №22)
А
В
С
1. Упростите выражения:
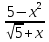
2. Сократите дроби:
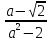 3. Решите уравнение, предварительно упростив его правую часть:
3. Решите уравнение, предварительно упростив его правую часть: 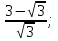
1. Упростите выражения:
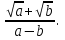
2. Сократите дроби: 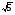 б)
б)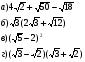
3. Докажите, что данное уравнение имеет целые корни, и найдите их:
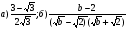
1. Упростите выражения:
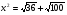
2. Сократите дроби: 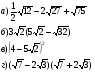
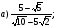
3. Решите уравнение:
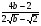
VIII. Итог урока
Заполните до конца оценочный лист. (Слайд №23). Оценки за урок.
Закончить урок я хочу стихотворением великого математика Софьи Ковалевской. (Слайд №24, 25)
Если в жизни ты хоть на мгновенье
Истину в сердце своем ощутил,
Если луч света сквозь мрак и сомненье
Ярким сияньем твой путь озарил:
Что бы в решенье твоем неизменном
Рок ни назначил тебе впереди,
Память об этом мгновенье священном
Вечно храни, как святыню в груди.
Тучи сберутся громадой нестройной,
Небо покроется черною мглой,
С ясной решимостью, с верой спокойной
Бурю ты встреть и померься с грозой.
В этом стихотворении выражено стремление к знаниям, умение преодолевать все преграды, которые встречаются на пути. Урок окончен. Спасибо за урок! (Слайд №26)
Приложение
ЛИСТ-ОПРОСНИК
Ф.И. ученика____________________________
1. Настроение в начале урока: а) б) в)
2. Мое восприятие темы урока:
а) усвоил(а) все; б) усвоил(а) почти все; в) усвоил(а) частично, нуждаюсь в помощи.
3. Количество неправильных ответов теста: _________
4. Я работал(а) на уроке:
а) отлично; б) хорошо; в) удовлетворительно; г) неудовлетворительно.
5. Я оцениваю свою работу на ______ (поставьте оценку)
6. Я оцениваю урок на _____ (поставьте оценку)
7. Настроение в конце урока: а) б в)
Тест
I вариант
1. Упростите выражение ![]()
![]()
1) ![]() 2)
2) ![]() 3)
3)![]()
2. Раскройте скобки и упростите выражение: ![]()
1) 18; 2) 12; 3) 22.
3. Упростите: 
1)![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() .
.
4. Освободитесь от иррациональности в знаменателе ![]() =
=
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() .
.
5. Вынесите множитель из-под знака корня: 
1)  ; 2)
; 2)  ; 3)
; 3) ; 4)
; 4)
Тест
II вариант
1. Упростите выражение ![]()
1) ;
;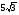 2)
2)  ; 3)
; 3)
2. Раскройте скобки и упростите ![]()
1) 8; 2) 12; 3) 10.
3. Упростите: 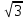
![]() ;
; ![]() ;
; ![]()
4. Освободитесь от иррациональности в знаменателе: 
1) ![]() ; 2)
; 2)![]() ; 3)
; 3) ![]() .
.
5. Вынесите множитель из-под знака корня: 
1) 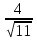 ; 2)
; 2)  ; 3)
; 3) ; 4)
; 4)