Урок -соревнование Применение производной

Истинное сокровище для людей - умение трудиться!

Эзоп

Урок-соревнование по теме «Применение производной»

Цели урока:

• обобщение изученного материала по теме,

• формирование умений применять математические задания к решению практических задач,

• развитие познавательной активности, творческих способностей, воспитание интереса к предмету,

Задачи урока:

• проверить знания студентов по теме «Производные функций» и умения вычислять производные;

• развитие познавательной самостоятельности на основе личностно -ориентированного подхода к студентам;

• формирование коммуникативной компетентности через нестандартную форму урока.

Тип урока: урок обобщения и систематизации знаний.

Урок проводится в виде игры -соревнования.

Правила игры:

• группа делится на две команды;

• выбираются капитаны команд;

• капитаны назначают консультантов;

• для участия во всех видах работы студенты вызываются к доске капитанами команд;

• правильные ответы оцениваются баллами, дается жетон.

Оборудование:

• школьный ПК;

• экран;

• карточки с заданиями;

• жетоны.

Организационный момент: постановка целей и задачей урока.

1 этап: Разминка (устно)

Найти ошибку. За каждый правильный ответ дается 1 балл.

2 этап: Конкурс капитанов

Капитанам предлагаются задачи, написанные на карточках:

• Задача 1. Представьте число 20 в виде суммы двух положительных чисел так, чтобы сумма их квадратов была наибольшей. (3 балла)

• Задача 2. Площадь участка земли составляет 100 м². Найти размеры участка, чтобы длина изгороди была наименьшей .(3 балла)

Во время решения капитанами задач команды выполняют самостоятельную работу. По результатам решения задач и самостоятельной работы, капитаны и команды получают соответствующие баллы.

Задания для самостоятельной работы:

Найти производную функции и значение производной в данной точке:f(x)= x³ +x² +3x

f(x)= x³ -x² +3x

2

f(x)= cos x, x₀ =

f(x)=-sin x, х₀=

4

f(x)= x³ ·2 sin x

f(x) = cos x· x^-4

4

f (x)=

f(x)=

4

3 этап: Блиц-турнир

Чья команда быстрее ответит на большее количество вопросов (1 балл за каждый правильный ответ).

• Кто ввел обозначение производной?

• Производная числа 6?

• Производная f(x)= x²?

• Производная f(x)= x^-3?

• Закончите предложение: если угловой коэффициент касательной к графику k>0 (k<0), то она образует с осью ОХ…

• Дать определение производной.

• Производная суммы равна…

• Когда функция возрастает?

• Что называется максимумом функции?

• Что называется минимумом функции?

4 этап: Конкурс эрудитов

Задания написаны на карточках. Выполняют 2 студента у доски. (3 балла)

5 этап: Задания для команд

Исследовать и построить график функции. (3 балла)

1 Вариант 2 Вариант

f (x)= 5 x² - x ³ f (x)= 5 x² - x ³ - 2

6 этап: Дополнительные задания для команд (8 баллов)

1 вариант

1. Что можно сказать о производной в точке экстремума?

2. На графике y=f' (x) укажите точки максимума и минимума

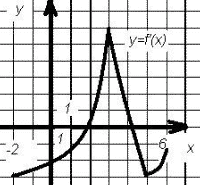
3. Найти промежуток возрастания функции f(x) = 3x³ - x² -7x

2 Вариант

1. Найти промежуток убывания функции y = 3x³ - x³ -7x

2. На рисунке изображен график функций y= f(x) и касательная к нему в точке x_0. Найти f'(x₀)

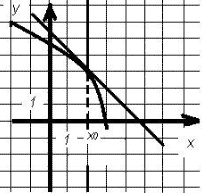
3. Найти промежуток возрастания функции f(x) = -x³ +2 x² +6x

7 этап: Подведение итогов

Конкурс капитанов

Блиц турнир

Конкурс капитанов

Задания для команд

Самостоятельная работа

Дополнительно

Итого

1команда

2команда

8 этап: Рефлексия

Вспомним, какие цели вы ставили перед собой в начале урока. Достигли ли вы их?

Понравился ли вам урок?

Домашнее задание:

• Придумать задачу практического содержания на нахождение наибольшего или наименьшего значений функции.

Выставление оценок:

• До 12 баллов- «2»;

• 13-18 баллов- «3»;

• 19-23 балла- «4»;

• больше 24 баллов- «5».

Литература:

• Ш.А. Алимов, учебник для 10-11 классов Алгебра и начала математического анализа М.: Просвещение, 2014.

• Журнал «Математика в школе».

• Карп, А.П. Даю уроки математики. М.: Просвещение, 2011.