- Учителю
- Панорамное занятие спецкурса по математике «Дифференциальное и интегральное исчисление» (в 11 классе)
Панорамное занятие спецкурса по математике «Дифференциальное и интегральное исчисление» (в 11 классе)
Панорамное занятие спецкурса по математике
«Дифференциальное и интегральное исчисление» в 11 классе
Учитель: Чернова Г.А., учитель математики школы-гимназии №17 г.Актобе
Тема: Повторение «Предел функции на бесконечности и предел функции в точке»
Цель:
Образовательная: повторение и закрепить теорию пределов и ее применение.
Познавательная: научиться считывать пределы, составлять уравнения асимптот.
Воспитательная: воспитывать у учащихся на уроке аккуратность, самостоятельность,
умение логически мыслить.
Ход урока:
Один из важнейших разделов математики- «Предел и непрерывность». Предел функции на бесконечности обозначается ![]() . Число
. Число ![]() называется пределом функции
называется пределом функции ![]() при
при ![]() , если
, если ![]() , где
, где ![]() - функция бесконечно малая при
- функция бесконечно малая при ![]() .
.
Свойства пределов при ![]() :
:
-
Функция
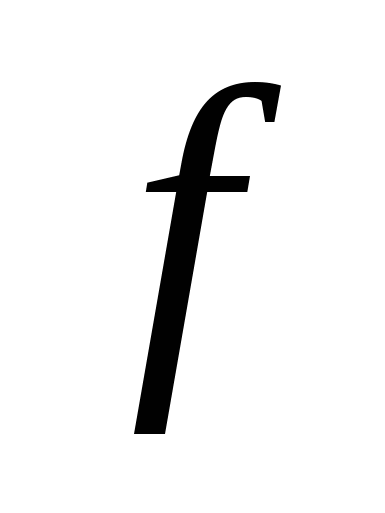 не может иметь двух различных пределов при
не может иметь двух различных пределов при  .
. -
Пусть
 и
и  . Предел суммы функций
. Предел суммы функций 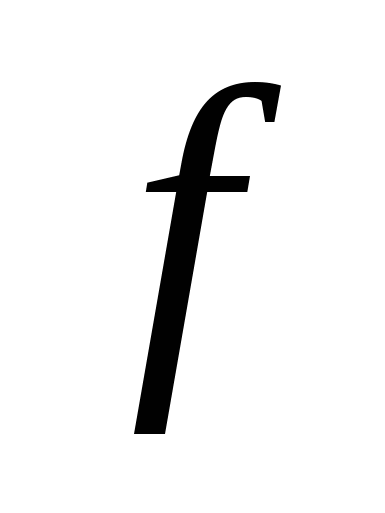 и
и 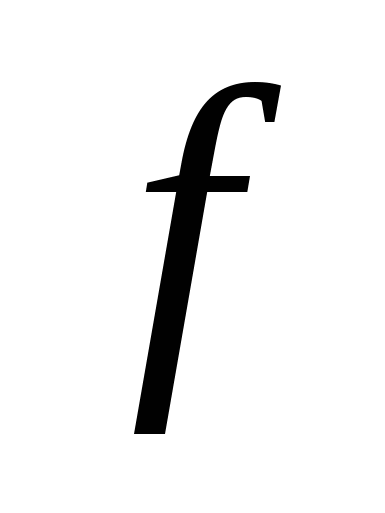 при
при  равен сумме пределов
равен сумме пределов 
-
Предел произведения функций
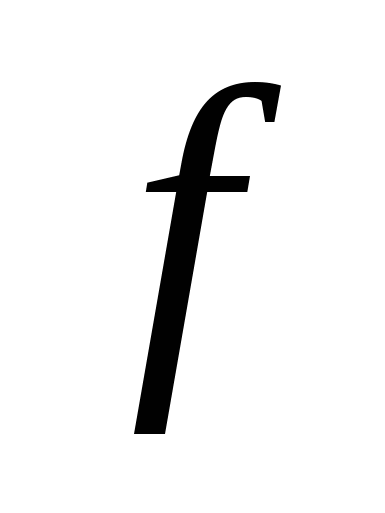 и
и 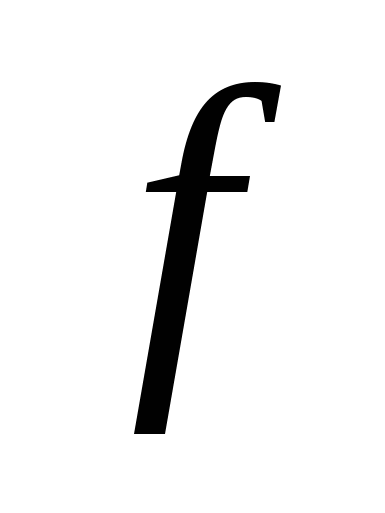 при
при  равен произведению их пределов
равен произведению их пределов 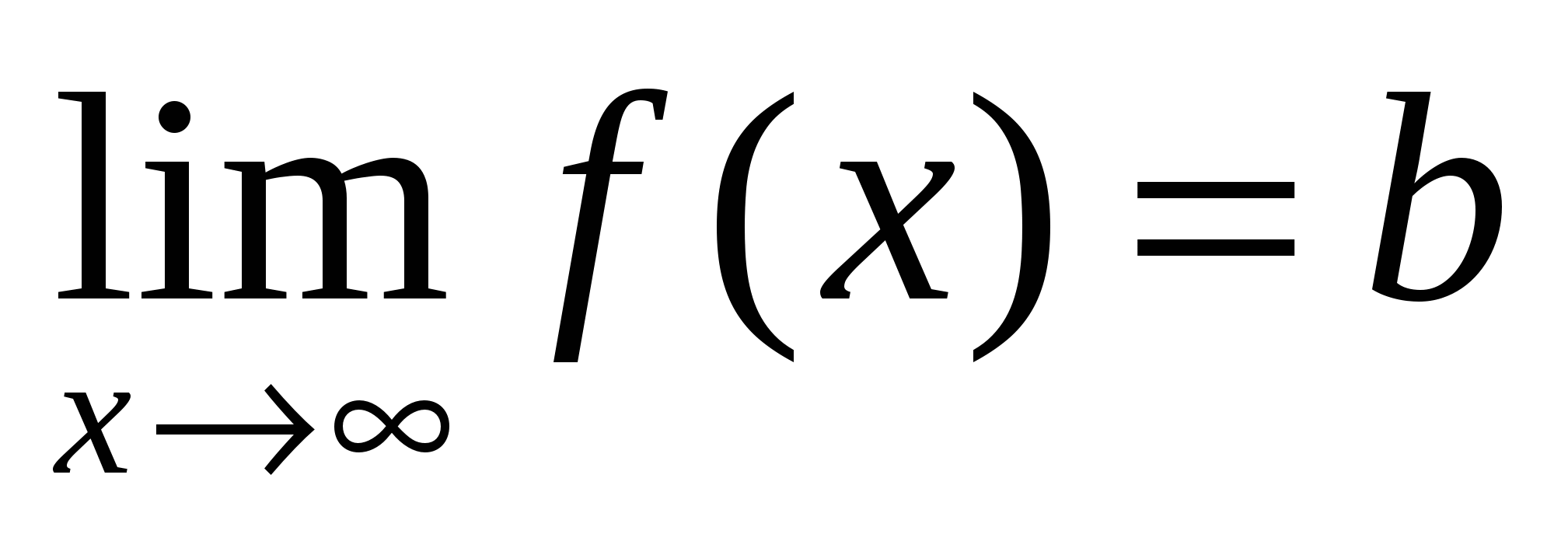
-
Если
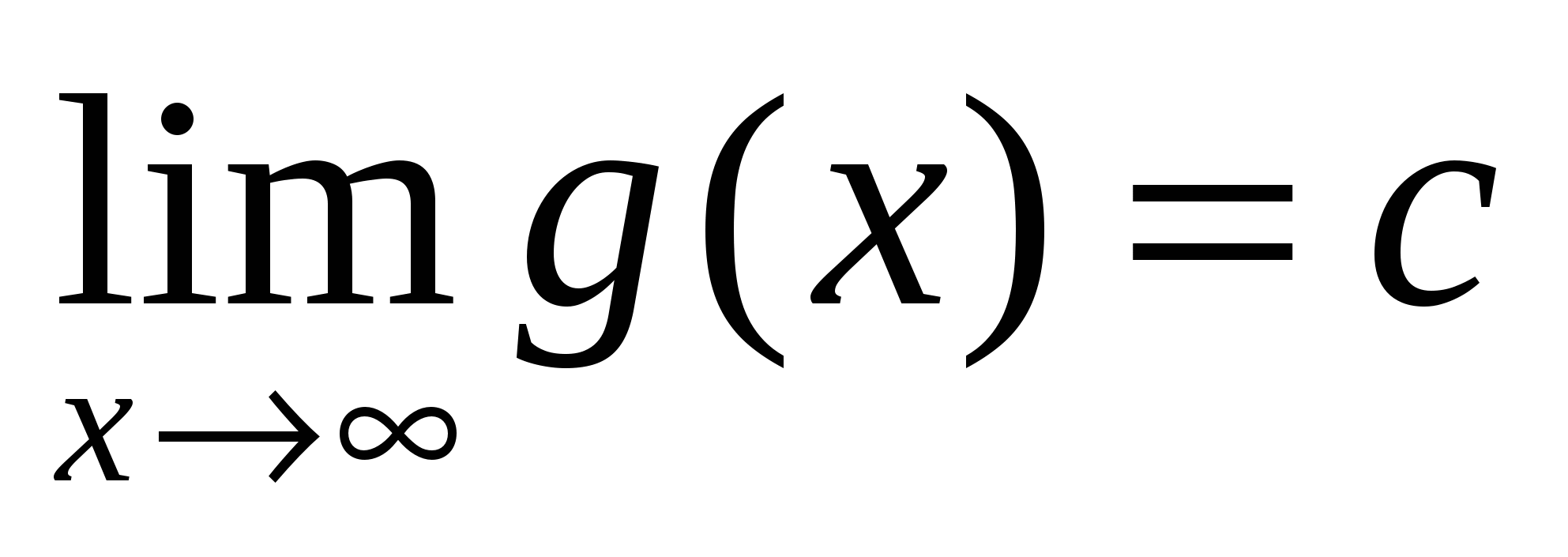 , то предел частного функций
, то предел частного функций 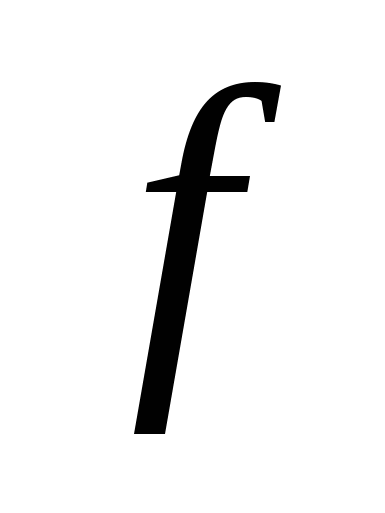 и
и 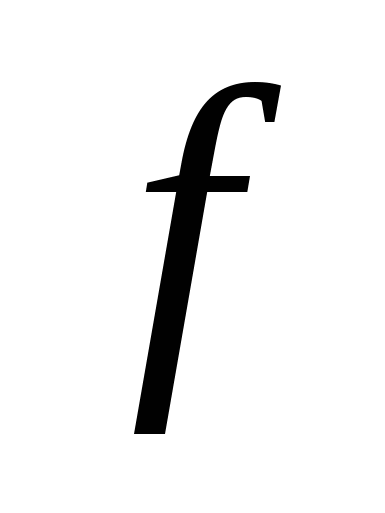 равен частному их пределов
равен частному их пределов 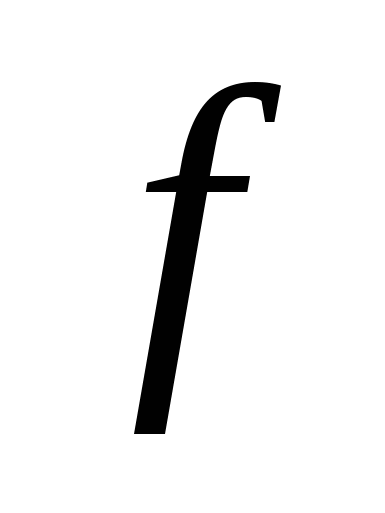
-
Предел бесконечно малой при
 равен 0, предел бесконечно большой при
равен 0, предел бесконечно большой при  равен
равен  .
.
-
Если функция
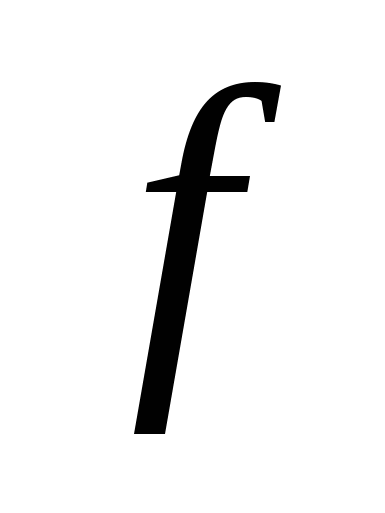 является частным двух многочленов одинаковой степени, то ее предел при
является частным двух многочленов одинаковой степени, то ее предел при  равен частному коэффициентов при старших степенях
равен частному коэффициентов при старших степенях  .
. -
Если степени числителя меньше степени знаменателя, то предел функции при
 равен 0.
равен 0. -
Если степень числителя больше степени знаменателя, то предел функции при
 равен
равен  .
.
Например:
Вычислить ![]() , если а)
, если а) ![]() ; б)
; б) ![]() ;
;
в) ![]() .
.
Определение. Число ![]() называют пределом функции
называют пределом функции ![]() при
при ![]() , если эта функция является суммой числа
, если эта функция является суммой числа ![]() и функции
и функции ![]() - бесконечно малой при
- бесконечно малой при ![]() , т.е.
, т.е. ![]() . Пишут
. Пишут ![]() .
.
Чтобы вычислить предел функции в точке, нужно вычислить значение функции в этой точке ![]() .
.
Если числитель и знаменатель- многочлены, то предел считается так: ![]() . Исключением является случай, когда при подстановке знаменатель обращается в нуль, в этом случае функцию надо упростить.
. Исключением является случай, когда при подстановке знаменатель обращается в нуль, в этом случае функцию надо упростить.
![]() .
.
Замечательные пределы:
1) ![]() ; 2)
; 2) ![]() .
.
Применяется теория пределов для составления уравнения асимптот, в определении производной, в выводе формулы площади криволинейной трапеции. Асимптота- это прямая, к которой стремится график функции, но с ней не сливается.
А) Уравнение горизонтальной асимптоты: ![]() ;
; ![]() .
.
Б) Уравнение вертикальной асимптоты: ![]() ;
; ![]() .
.
В) ![]() - уравнение наклонной асимптоты.
- уравнение наклонной асимптоты. ![]() ;
; ![]() .
.
Примеры:
а) ![]() ;
;
б) 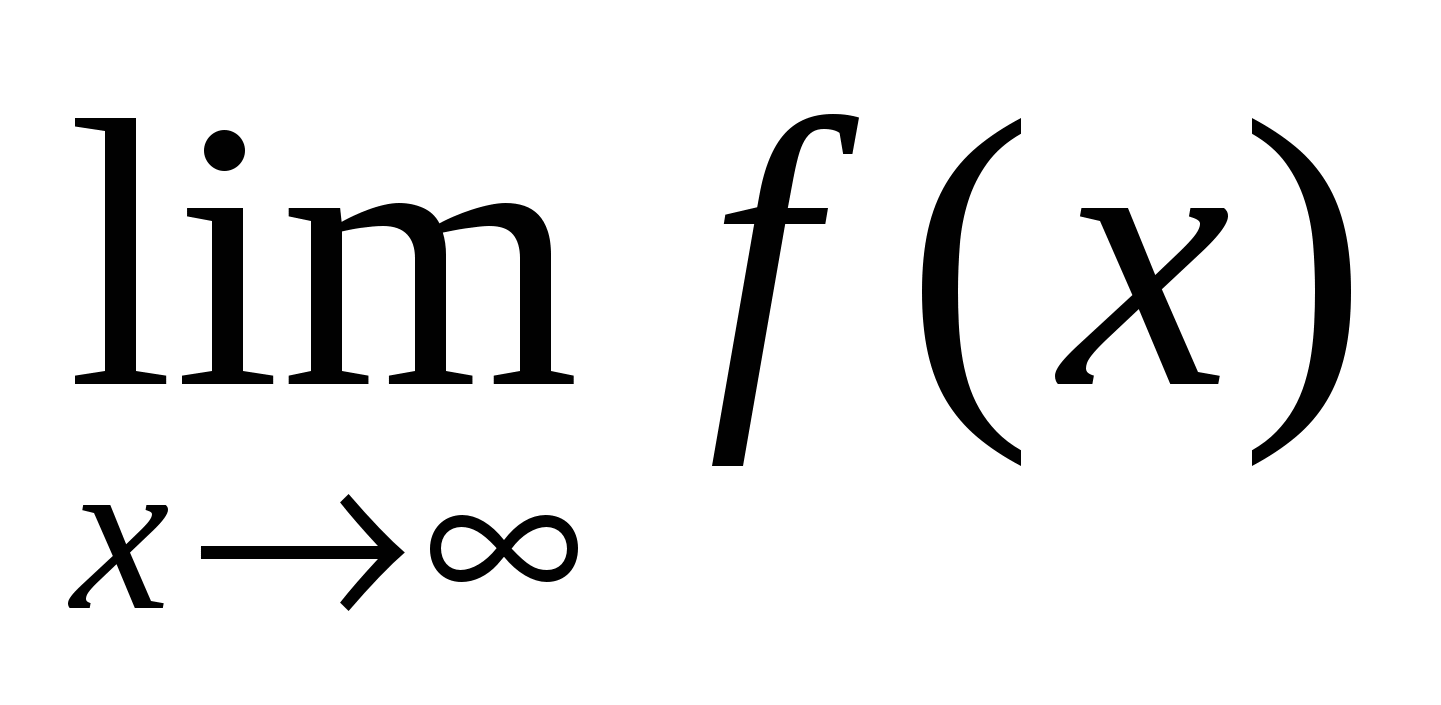 ;
;
в) ![]() ;
;
г) 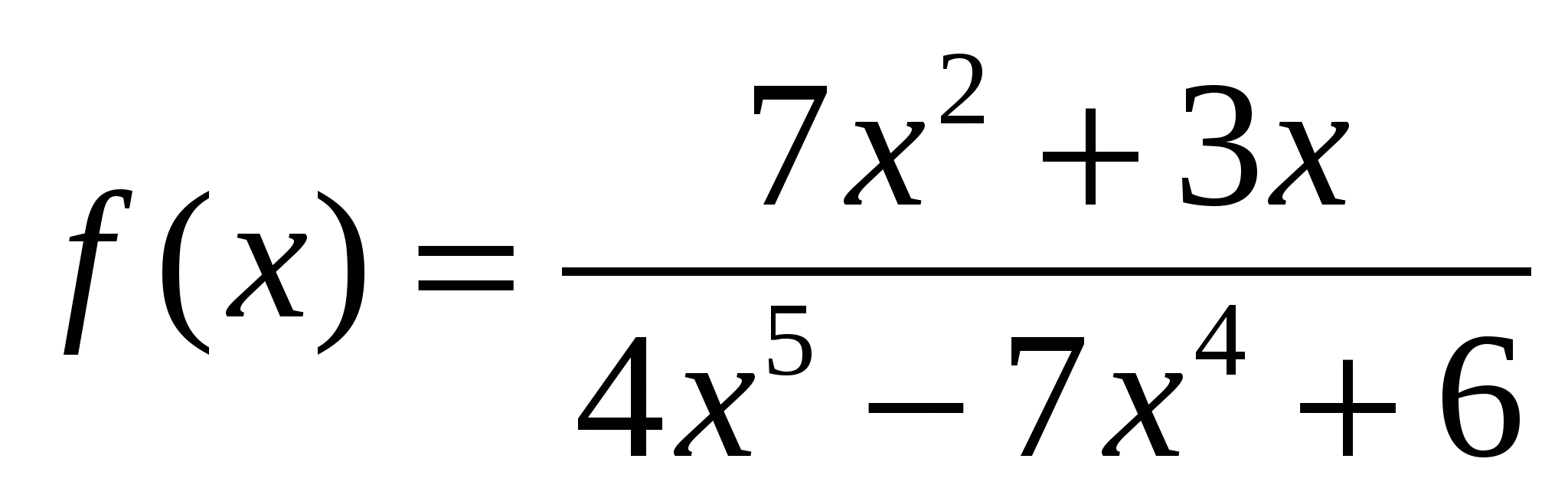 ;
;
д) ![]() .
.
Найти асимптоты графика функции ![]() .
.
1. точек разрыва нет ![]() нет вертикальных асимптот.
нет вертикальных асимптот.
2. ![]() - горизонтальных нет.
- горизонтальных нет.
3. Найдем наклонную асимптоту ![]() .
.
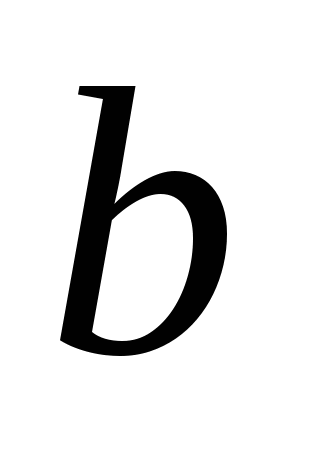
![]() .
. ![]()
Итак, мы повторили тему «Теория пределов» и применение. Теория пределов помогает нам более полно исследовать функцию и построить ее график, вычислять производные некоторых функций.