- Учителю
- Тренировочный вариант по математике №4 (от 21.04.2016) с критериями.
Тренировочный вариант по математике №4 (от 21.04.2016) с критериями.
Общий государственный экзамен, 2016 г.
МАТЕМАТИКА, 9 класс
Тренировочный вариант №4 от 21.04.2016
10/ 11
Общий государственный экзамен
по МАТЕМАТИКЕ
Инструкция по выполнению работы
Работа состоит из трёх модулей: «Алгебра», «Геометрия», «Реальная математика». Всего в работе 26 заданий. Модуль «Алгебра» содержит 11 заданий: в части 1 - восемь заданий; в части 2 - три задания. Модуль «Геометрия» содержит восемь заданий: в части 1 - пять заданий; в части 2 - три задания. Модуль «Реальная математика» содержит семь заданий: все задания этого модуля - в части 1.
На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).
Ответы к заданиям 2, 3, 8, 14 записываются в виде одной цифры, которая соответствует номеру правильного ответа. Эту цифру запишите в поле ответа в тексте работы.
Для остальных заданий части 1 ответом является число или последовательность цифр, которые нужно записать в поле ответа в тексте работы. Если в ответе получена обыкновенная дробь, обратите её в десятичную. В случае записи неверного ответа на задания части 1 зачеркните его и запишите рядом новый.
Решения заданий части 2 и ответы к ним запишите на отдельном листе или бланке. Задания можно выполнять в любом порядке, начиная с любого модуля. Текст задания переписывать не надо, необходимо только указать его номер.
Сначала выполняйте задания части 1. Начать советуем с того модуля, задания которого вызывают у Вас меньше затруднений, затем переходите к другим модулям. Для экономии времени пропускайте задание, которое не удаётся выполнить сразу, и переходите к следующему. Если у Вас останется время, Вы сможете вернуться к пропущенным заданиям.
Все необходимые вычисления, преобразования и т.д. выполняйте в черновике. Записи в черновике не учитываются при оценивании работы. Если задание содержит рисунок, то на нём непосредственно в тексте работы можно выполнять необходимые Вам построения. Рекомендуем внимательно читать условие и проводить проверку полученного ответа.
При выполнении работы Вы можете воспользоваться справочными материалами.
Баллы, полученные за верно выполненные задания, суммируются. Для успешного прохождения итоговой аттестации необходимо набрать в сумме не менее 8 баллов, из них не менее 3 баллов в модуле «Алгебра», не менее 2 баллов в модуле «Геометрия» и не менее 2 баллов в модуле «Реальная математика». За каждое правильно выполненное задание части 1 выставляется 1 балл. В каждом модуле части 2 задания оцениваются в 2 балла.
Желаем успеха!Для заданий с выбором ответа из четырёх предложенных вариантов выберите один верный ▪ В бланке ответов №1 поставьте знак «×» в клеточку, номер которой соответствует номеру выбранного Вами ответа. ▪ Для заданий с кратким ответом полученный результат сначала запишите на листе с текстом работы после слова «Ответ». Если получена обыкновенная дробь, обратите её в десятичную ▪ Перенесите ответ в бланк ответов №1 справа от номера соответствующего задания, начиная с первой клеточки. Каждый символ (цифру, знак минус, запятую или точку с запятой) пишите в отдельной клеточке в соответствии с приведёнными в бланке образцами. Единицы измерений указывать не нужно. ▪ Если при решении задания найдено несколько корней, запишите их (в любом порядке) в бланк ответов № 1, разделив точкой с запятой(;). Ответом к заданиям является последовательность цифр. Перенесите цифры
Часть 1
Модуль «Алгебра»
. Расположите в порядке убывания: 
1) 
2)
3)
4)
Ответ: ___________________________.
Ответ: ___________________________.
Ответ: ___________________________.
.
Ответ: ___________________________.
Установите соответствие между графиками функций и формулами , которые их задают .
-
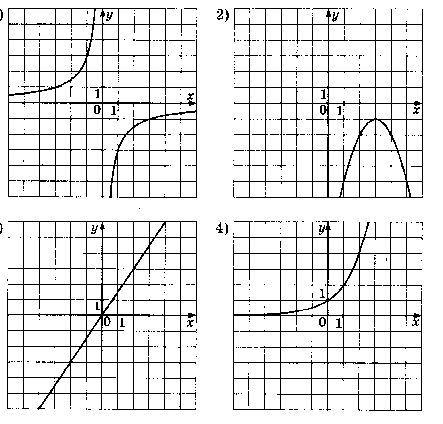
y =
-
y =
-
y =
Ответ: ___________________________.
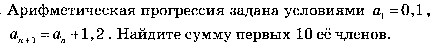
Ответ: __________________________.
Ответ: ___________________________.
Ответ: ___________________________.
Не забудьте перенести все ответы в бланк ответов № 1 в соответствии с инструкцией по выполнению работы.
Модуль «Геометрия»
.
Ответ: ___________________________.
Ответ: ___________________________.
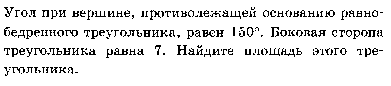
Ответ: ___________________________.
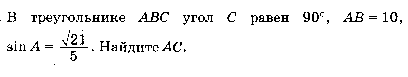
Ответ: _________________________.
|
13 |
Ответ: ________________________
Модуль «Реальная математика»
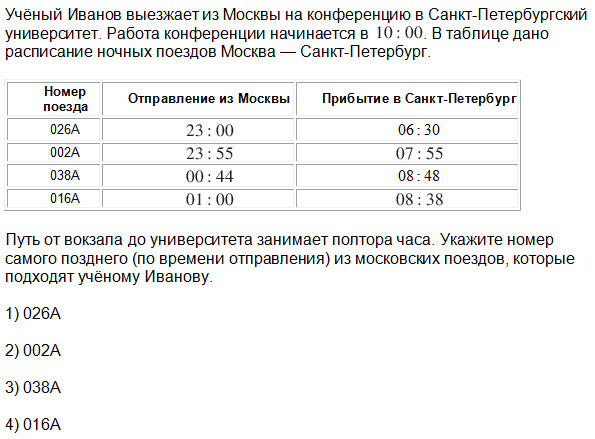
Ответ: ________________________
В нескольких эстафетах, которые проводились в школе, команды показали следующие результаты:
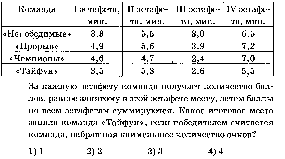
Ответ: ________________________
Ответ: ________________________
Ответ: ________________________
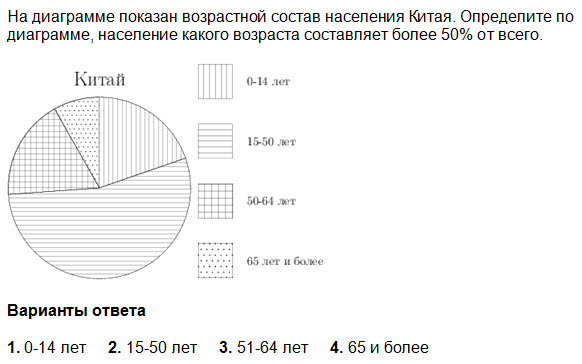
Ответ: ________________________
|
19 |
Ответ: ________________________
.
Ответ: ________________________
При выполнении заданий 21-26 используйте отдельный лист. Сначала укажите номер задания , а затем запишите его решение и ответ . Пишите чётко и разборчиво .
Модуль « Алгебра»
Сократите дробь 
Первый сплав содержит 5% меди, второй - 11% меди. Масса второго сплава больше массы первого на 4 кг. Из этих двух сплавов получили третий сплав, содержащий 10% меди. Найдите массу третьего сплава.
Постройте график функции 
И определите, при каких значениях 
прямая 
имеет с графиком ровно одну общую точку.
Модуль « Геометрия»
Биссектриса угла A параллелограмма ABCD пересекает его сторону BC
в точке E. Найдите площадь параллелограмма ABCD, если BE = 7 , EC = 3 ,
а ÐABC =150°.
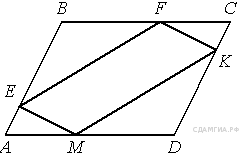В
параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как
показано на рисунке, причём АЕ = CK, СF = АM. Докажите, что EFKM -
параллелограмм.
В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 208. Найдите стороны треугольника ABC.
Система оценивания экзаменационной работы по математике
За правильный ответ на задания 1-20 ставится 1 балл.
|
14 |
2 |
|
15 |
1 |
|
16 |
3000000 |
|
17 |
2000 |
|
18 |
2 |
|
19 |
0,1 |
|
20 |
0,004 |
Решения и критерии оценивания заданий части 2
Модуль «Алгебра»
Сократите дробь
Решение.
Имеем:
Ответ: 
Правильно выполнены преобразования, получен верный ответ.
2
Решение доведено до конца, но допущена ошибка или описка
вычислительного характера (например, при вычитании), с её учётом дальнейшие шаги выполнены верно.
1
Другие случаи, не соответствующие указанным выше критериям.
0
Максимальный балл
2
Первый сплав содержит 5% меди, второй - 11% меди. Масса второго сплава больше массы первого на 4 кг. Из этих двух сплавов получили третий сплав, содержащий 10% меди. Найдите массу третьего сплава.
Решение.
Пусть масса первого сплава x кг. Тогда масса второго сплава (x + 4) кг, а третьего - (2x + 4) кг. В первом сплаве содержится 0,05x кг меди, а во втором - 0,11(x + 4) кг. Поскольку в третьем сплаве содержится 0,1(2x + 4) кг меди, составим и решим уравнение:
Откуда 
Масса третьего сплава равна 6 кг.
Ответ:6 кг.
Правильно составлено уравнение, получен верный ответ
2
Правильно составлено уравнение, но при его решении допущена вычислительная ошибка, с её учётом решение доведено до ответа
1
Другие случаи, не соответствующие указанным выше критериям.
0
Максимальный балл
2
Постройте график функции
И определите, при каких значениях
прямая
имеет с графиком ровно одну общую точку.
Решение.
Упростим выражение:
График функции сводится к графику параболы 
с выколотой точкой 
Этот график изображён на рисунке:
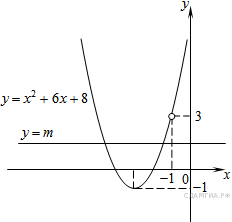
Из графика видно, что прямая
имеет с графиком функции ровно одну общую точку при 
и 
Ответ: −1; 3.
График построен правильно, верно указаны все значения m , при которых прямая y=m имеет с графиком только одну общую точку.
2
График построен правильно, указаны не все верные значения m.
1
Другие случаи, не соответствующие указанным выше критериям.
0
Максимальный балл
2
Модуль «Геометрия»
Биссектриса угла A параллелограмма ABCD пересекает его сторону BC
в точке E. Найдите площадь параллелограмма ABCD, если BE 7 , EC 3 ,
а ABC 150
Получен верный обоснованный ответ.
2
При верных рассуждениях допущена вычислительная ошибка, возможно приведшая к неверному ответу.
1
Другие случаи, не соответствующие указанным выше критериям.
0
Максимальный балл
2
В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём АЕ = CK, СF = АM. Докажите, что EFKM - параллелограмм.
Решение.
Противоположные
стороны параллелограмма равны и по условию 
следовательно:
В параллелограмме противоположные углы равны: 
, 
Рассмотрим треугольники 
и 
, в этих треугольниках
, 
, 
следовательно эти треугольники равны, а значит, 
. Аналогично равны треугольники 
и 
а следовательно равны отрезки 
и 
Противоположные стороны четырехугольника 
равны, следовательно, по признаку параллелограмма, этот
четырёхугольник - параллелограмм.
Доказательство верное, все шаги обоснованы.
2
Доказательство в целом верное, но содержит неточности.
1
Другие случаи, не соответствующие указанным критериям
0
Максимальный балл
2
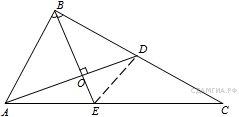
В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и
имеют одинаковую длину, равную 208. Найдите стороны треугольника
ABC.
Решение.
Пусть
- точка пересечения отрезков 
и 
(см. рис.). Треугольник 
- равнобедренный, так как его биссектриса 
является высотой. Поэтому
;
.
По свойству биссектрисы треугольника
Проведём через вершину 
прямую, параллельную 
. Пусть 
- точка пересечения этой прямой с продолжением медианы
. Тогда 
Из подобия треугольников 
и 
следует, что 
Поэтому 
и 
Следовательно,
;
;
Ответ: 
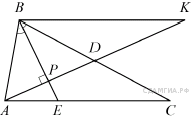
Приведём другое решение.
Треугольники
и 
равны: они прямоугольные, углы 
и 
равны, сторона 
- общая. Тогда 
и 
Заметим далее, что 
а тогда 
Биссектриса треугольника делит сторону, к которой она проведена, на
от-резки пропорциональные прилежащим сторонам, поэтому 
откуда 
Найдём 
и 
Треугольники
и 
равны: 
углы и
равны,
- общая сторона, поэтому 
Медиана 
тре-угольника 
делит его на два равновеликих, поэтому справедливо равенство:
Тем самым, 
Наконец, площадь треугольника
равна половине площади треугольника 
откуда
Площадь выпуклого четырёхугольника равна половине произведения длин диаго-налей на синус угла между ними, поэтому:
Тогда: 
С другой стороны, 
откуда
Длину
найдём по теореме Пифагора из прямоугольного треугольника
Значит, 
Длину 
найдём по теореме Пифагора из прямоугольного тре-угольника
тогда:
Поэтому
Ответ: 
Доказательство верное, все шаги обоснованы.
2
Доказательство в целом верное, но содержит неточности.
1
Другие случаи, не соответствующие указанным критериям
0
Максимальный балл
2
© 2016 Всероссийский проект «Самоподготовка к ОГЭ»
vk.com/oge100ballov
Составитель: Д.В. Владимиров
Разбор всех заданий:
vk.com/oge100ballov/2016kim01</</p>
Разрешается свободное копирование в некоммерческих образовательных целях
